压电管堆式宽带换能器*

尹义龙 莫喜平张运强崔 斌

(1中国科学院声学研究所 北京100190)

(2北京海洋声学装备工程技术研究中心 北京100190)

0 引言

压电陶瓷圆管是一种经典的水声换能器结构，被广泛应用于水声计量、探测及通信等领域。近年来，国内外学者在压电圆管换能器宽带、低频、大功率等方面开展了大量研究工作[1-7]。圆管换能器宽带设计的主要思路是利用多阶模态耦合拓展换能器的工作带宽，如利用径向、液腔耦合实现宽带发射的溢流换能器[1]，利用圆管自身纵向、径向、弯曲等模态耦合的空气背衬换能器[3-5]，利用附加无源结构带来的多阶模态提高换能器宽带的复合换能器等[2,7]。在低频方面，高效的极化方式和新型的换能器结构相结合为新型圆管换能器的设计提供了技术途径。其中，切向极化的镶拼圆管是目前较为成熟的结构，在此基础上发展出的开口圆管、复合圆管[2]等新的圆管换能器在低频、宽带、大功率方面取得了较大的突破[7-11]。

切向极化的镶拼圆管是由高精度的楔形条拼合而成，主要应用于中低频段换能器的设计。现阶段，高频圆管换能器仍然使用传统径向极化压电陶瓷圆管结构。径向极化压电陶瓷圆管的结构简单且成本低廉，但是压电陶瓷31振动模式的压电参数较低，在实现高灵敏度、宽带发射方面有一定技术难度。本文提出了一种压电管堆式宽带圆管换能器结构，使用多个纵向极化的薄壁压电陶瓷圆管组成管状压电叠堆(简称压电管堆)，利用压电管堆的33振动模式提高换能器的发射性能，通过纵向振动和径向振动耦合实现宽带工作。与镶拼圆环结构相比，组成压电管堆的陶瓷环结构更加简单，在小尺寸情况下易于实现，可以作为中高频宽带大功率圆管换能器的一种良好解决方案。

1 压电管堆纵径耦合分析

压电管堆结构如图1所示，由多个纵向极化的薄壁压电陶瓷圆管沿轴向粘接而成，单元间采用电学并联方式工作，总高度h，平均半径为a，厚度为t。压电管堆的振动方程和边界条件可以参考径向极化薄壁圆管的情况[12-14]，当壁厚远小于其他尺寸时压电圆管在厚度方向不存在应力波，即有T2=0,T6=0，而且在对称激励下换能器的振动也是对称的，因此有T4=0,T5=0。根据以上边界条件，使用d型压电方程可得

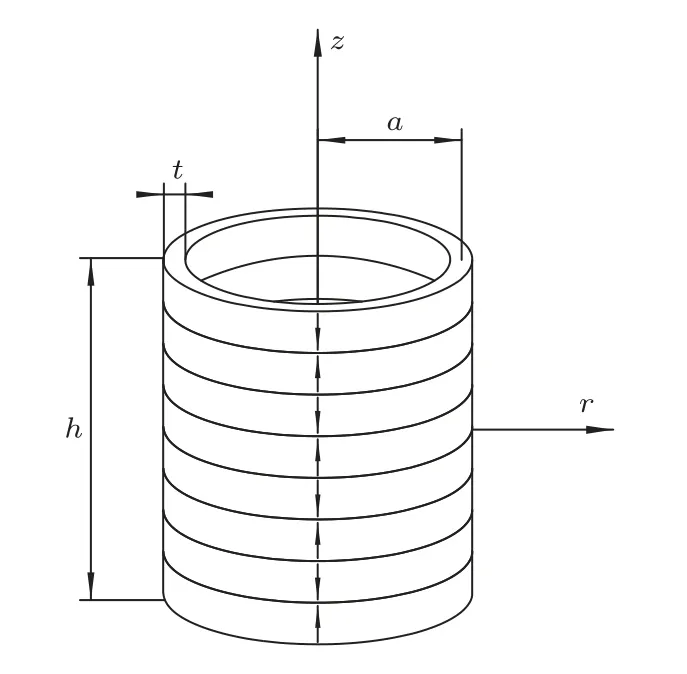
图1 压电管堆结构图Fig.1 The sketch of the piezoelectric cylindrical stack

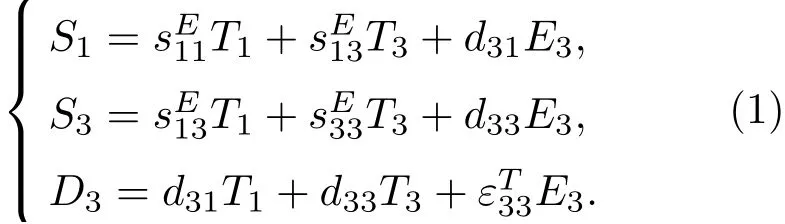
由压电方程可求得径向应力T1、纵向应力T3的表达式：

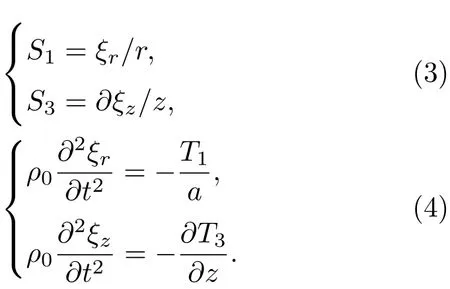
将式(2)及式(3)代入式(4)的振动方程，简化得到压电管堆纵向简谐振动方程：

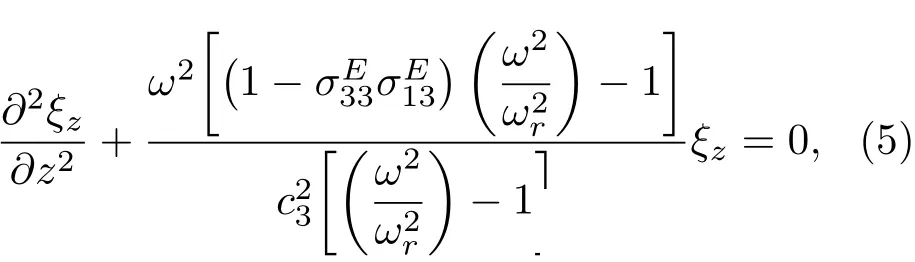
令：

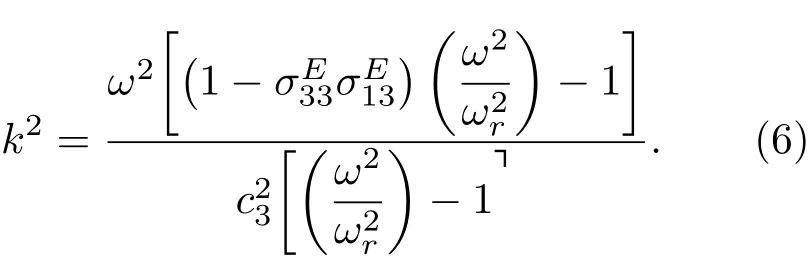
根据压电圆管两端自由和对称激励的边界条件可知换能器振动节点应在中心位置，振动方程的解为

考虑换能器在高度方向只存在一个节点的低阶振动情况，振幅在两端位置最大，即k=π/h，定义换能器的高径比α=h/a，由此可得圆管振动的频率方程：

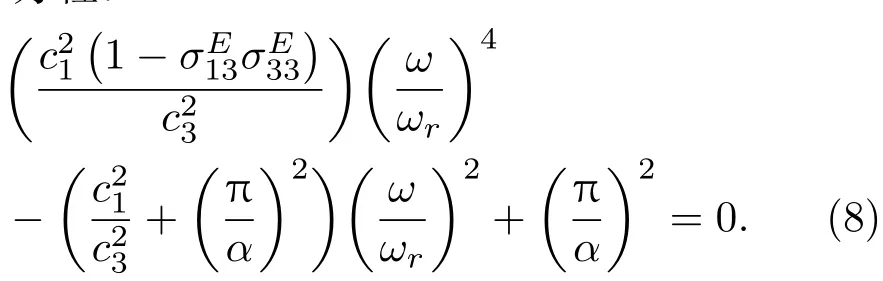
与文献[13]中径向极化陶瓷圆管相比，纵向极化压电管堆的频率方程的不同主要是考虑了极化方向弹性常数和声速的变化。由图2可以看出，由于纵向极化方式下33方向弹性常数有所降低，其纵振动频率要比径向极化方式下略低，而换能器的径向谐振频率基本相同。换能器的谐振频率是高径比的函数，在高径比α=π附近换能器两阶谐振距离较近，此时换能器高度和径向振动产生较强的振动耦合。

根据频率方程(8)的两个实数解定义两阶谐振频率之差为

求解式(9)的极小值可以获得两阶谐振频率距离最近时的高径比参数，即

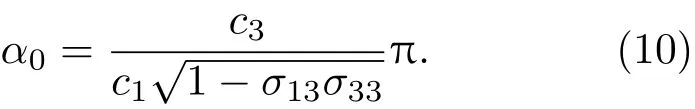
高径比α0可以看作是压电管堆纵径耦合振动的临界点，如选用PZT-4压电陶瓷,计算得到α0≈3.0。当α≪α0时，换能器的一阶谐振倾向于径向振动模态，二阶谐振倾向于纵向振动模态；当α≫α0时一阶谐振更倾向于纵向振动模态，而二阶谐振倾向于径向振动模态；α=α0附近是换能器模态转换的区域，此时换能器纵向及径向模态将产生强烈的振动耦合。可以看出，压电管堆结构的振动模态主要与高径比参数有关，α=α0附近是换能器纵向及径向振动的强耦合区，在此参数区间内对换能器的发射响应进行优化可以获得较好的宽带性能。

2 压电管堆仿真与优化

有限元方法是水声换能器领域常用的数值分析方法，能够计算换能器振动位移分布、发射电压响应等具体参数，结合理论结果可以更深入地了解换能器的振动辐射特性。根据压电管堆的结构特点建立如图3所示的轴对称模型，换能器由8个纵向极化的薄壁压电陶瓷圆管单元沿高度粘接而成，单元间采用电学并联方式连接，压电材料选用PZT-4压电陶瓷。

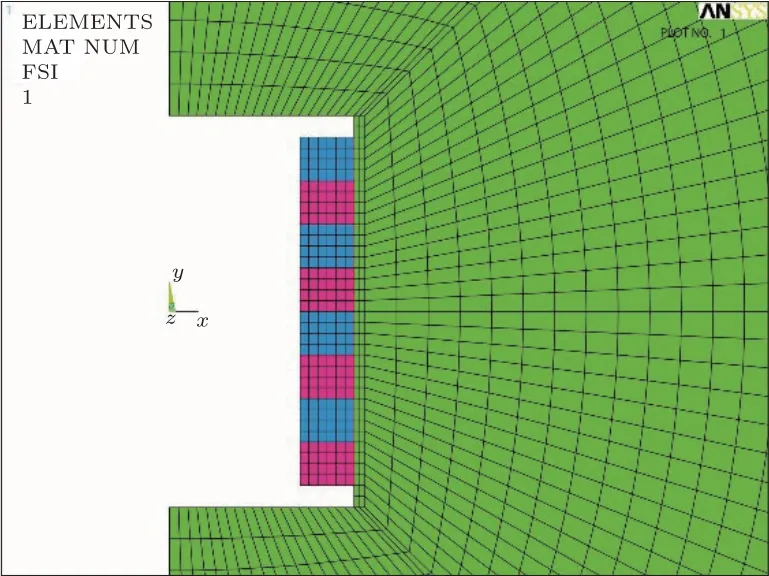
图3 换能器有限元模型Fig.3 The finite element model of the transducer

2.1 换能器振动辐射特性研究

利用有限元模型计算空气中谐振频率随高径比变化曲线如图4所示，其中理论曲线是由式(8)得计算得到。当圆管高径比较小时仿真曲线与理论曲线符合较好，特别是一阶谐振频率与理论结果基本相同。随着高径比增大，仿真曲线与理论曲线在二阶谐振频率附近出现了较大的差异，代表换能器径向振动的二阶谐振逐渐减弱并消失，在此频率附近出现了以弯曲为主的振动模态。

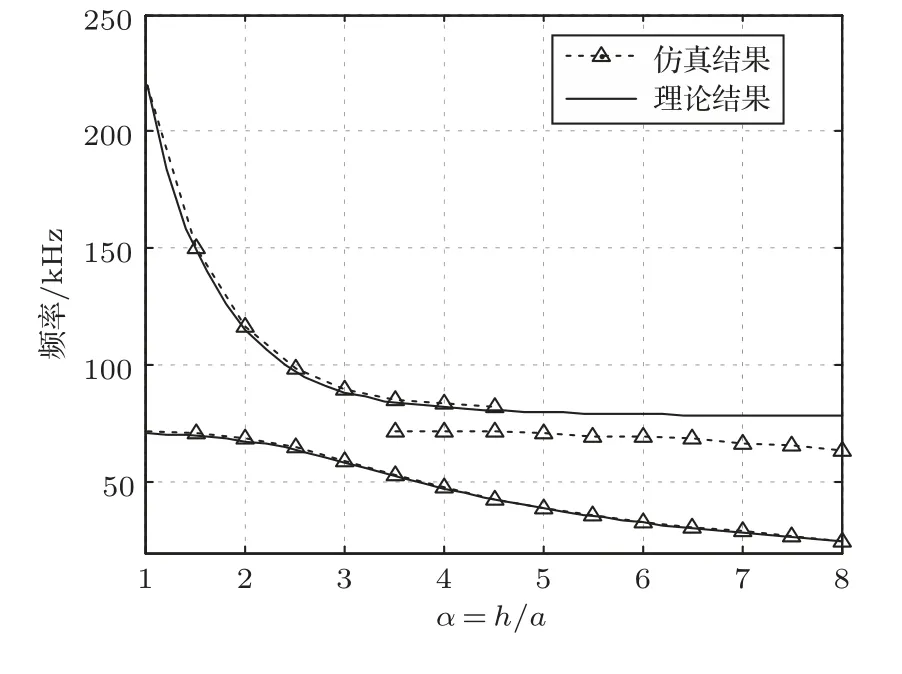
图4 压电管堆谐振频率随高径比变化的仿真曲线Fig.4 The resonance frequency of the simulation model as a function of aspect ratio h/a

在管堆直径和厚度不变的情况下调节换能器高度，获得不同高径比参数下换能器主要模态的振动位移矢量图，分别为短管堆(α=1)、强耦合(α=3)、长管堆(α=6)三种情况。在管堆较短时(α=1)，短管的两阶谐振频率分别是较为纯正的径向振动和纵向振动，具体振型如图5(a)及图5(b)所示，其中径向谐振频率为72 kHz，纵向谐振频率为220 kHz。随着管堆高度增加，谐振频率逐渐降低且振动耦合增强。当α=3时,管堆的两阶振动模态如图6(a)及图6(b)所示，可以看出两种振动模态的位移中均包含了径向振动及纵向振动分量，纵向和径向的振动耦合非常明显。当高度继续增加至α=6，换能器第一阶模态已经由短管时的径向振动模态转变为长管的纵向振动模态，在高频段换能器的径向振动存在明显的振动节点，呈现出弯曲振动形式。

典型的圆管径向振动是位移均匀分布的呼吸振动模态，当管堆较长时换能器已经不存在纯正的呼吸振动模态，径向振动沿高度方向出现节点，呈现出一种轴对称的径向弯曲振动，如图7(b)所示。在弯曲振动模态下圆管表面存在多个振动节点与反相区，反相区的存在会严重降低换能器的辐射效率。由此可见，在压电管堆换能器的设计中高径比参数应控制在较小的区域，避免管堆过长而出现弯曲振动。

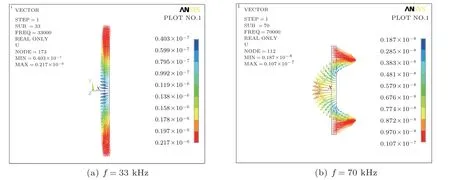
图7 长管堆情况下的主要模态振型图(α=6)Fig.7 The displacement of vibration modes at the aspect ratio α=6

圆管换能器的纵向振动和径向振动常存在反相的情况，在如图5所示的短圆管参数下，由于振动模式较为纯正，这一问题通常可以忽略。而在图6中强耦合状态下，其振动位移中均包含了明显的纵向和径向振动分量，因此两个方向的振动位移反相要严重的多。如图6(a)所示,当圆管径向收缩时高度做伸长运动，径向与高度的声辐射相位相反。虽然高度方向的辐射面非常小，但是反相振动也会严重降低换能器的辐射效率。为了解决强耦合状态下高度与径向辐射的反相问题，在圆管的两端使用泡沫反声材料进行声屏蔽，只利用径向进行声辐射。

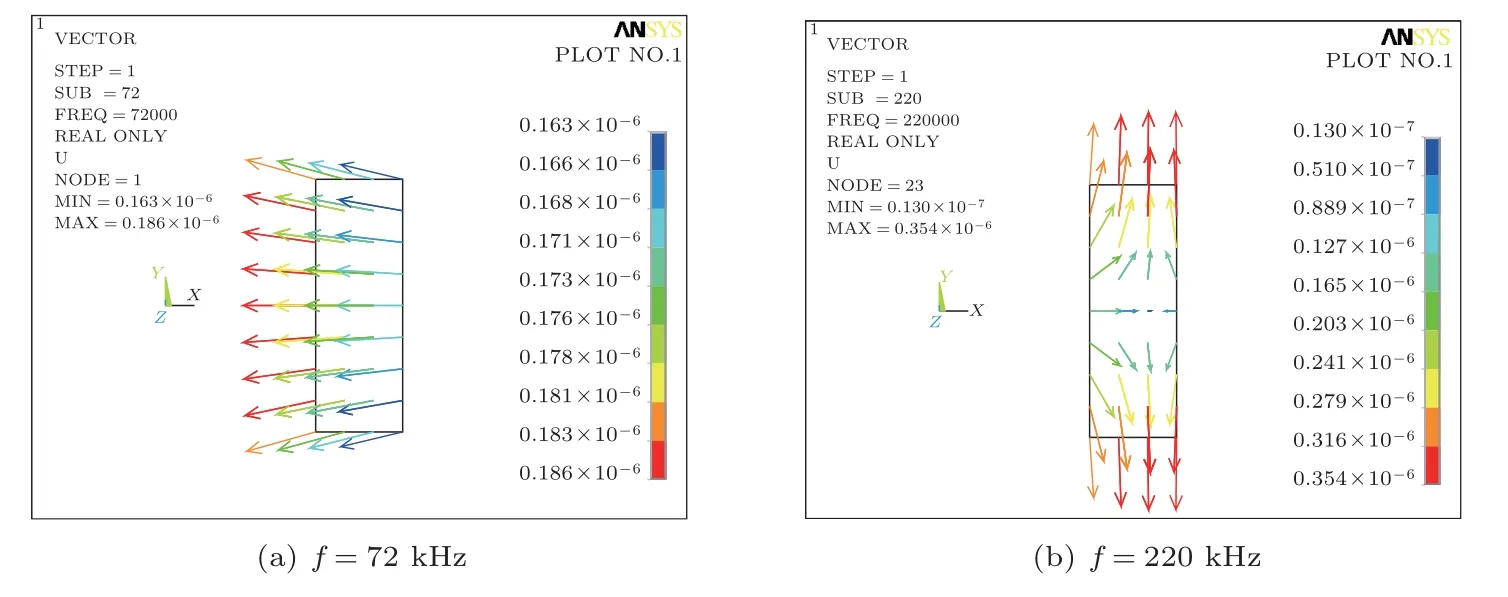
图5 短管堆情况下的主要模态振型图(α=1)Fig.5 The displacement of vibration modes at the aspect ratio α=1

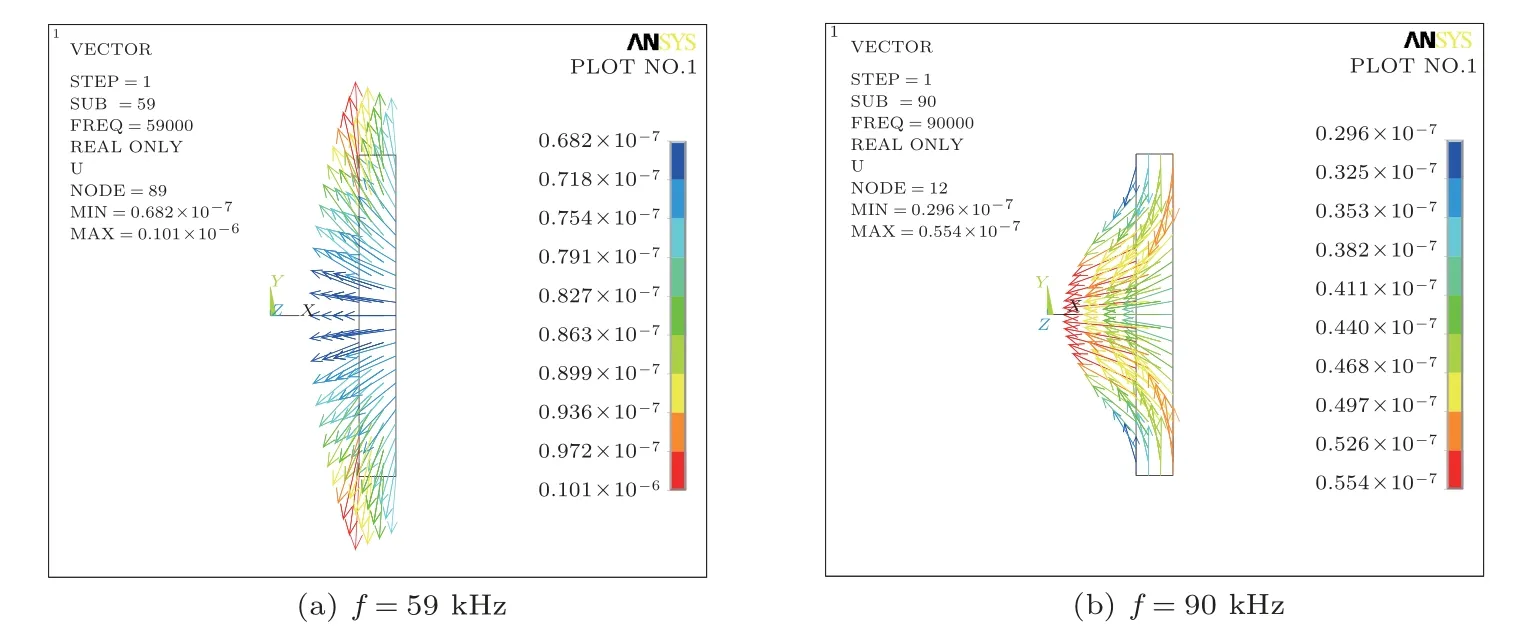
图6 强耦合情况下的主要模态振型图(α=3)Fig.6 The displacement of vibration modes at the aspect ratio α=3

2.2 换能器发射特性优化

通过理论及仿真结果可知，压电管堆换能器的振动及辐射特性主要与高径比参数有关。在保证施加电场强度不变的情况下，通过调节换能器的高度获得不同高径比情况下的发射电压响应曲线，仿真结果如图8所示。在高径比较小时，换能器两阶谐振频率的距离较远，此时低频谐振峰应为纯径向振动，频率约为68 kHz。随着高径比升高，纵向谐振频率迅速降低，纵径振动耦合增强，带内起伏逐渐变小。当高径比继续增加超过临界点时，换能器出现图5中的弯曲振动模态，高频段的发射电压响应迅速降低，并且在两阶谐振之间出现响应凹坑。

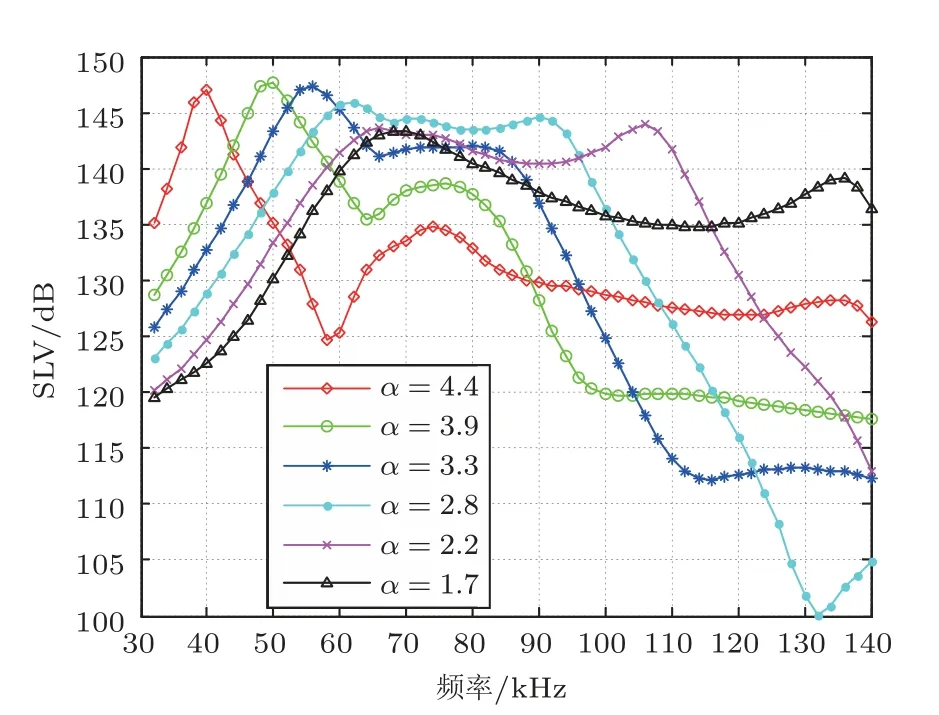
图8 不同高径比下换能器发射电压响应曲线仿真结果Fig.8 The transmitting voltage response of the transducer model at different aspect ratios

图9是两个谐振峰处的发射电压响应SLVω1与SLVω2随高径比α的变化曲线。换能器的低频响应峰值SLVω1随着α的增加逐渐升高，在超过α=α0的临界点后，也就是低频谐振由径向振动转变为纵向振动模态后，发射电压响应的变化趋于平稳。高频响应峰值SLVω2随α变化出现极值点，当α=2.4时达到最大，随后逐渐降低。如果选取高径比参数使两种模态响应幅值相当，可以在两个谐振频率间形成最佳宽带效果。

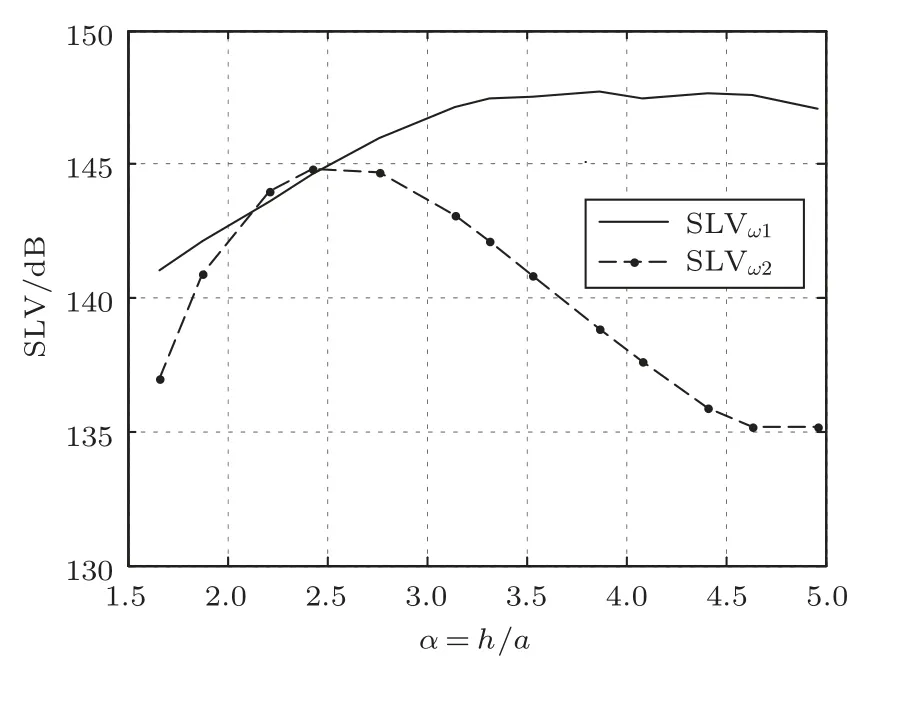
图9 换能器峰值响应随高径比参数的变化Fig.9 The transmitting voltage response at resonance frequency as a function of aspect ratio h/a

在以上分析的基础上初步确定换能器样机的尺寸参数，获得换能器发射电压响应仿真结果如图10所示，其中径向极化圆管换能器由两段去耦的短圆管组成，这种结构相比单个长圆管性能更佳[15-16]。在两种类型的换能器上施加了相同电场强度的激励，可以看出纵向极化下圆管换能器的发射性能具有明显优势，带宽比径向极化压电圆管提高了一倍以上，带内发射电压响应提高至少3 dB以上。

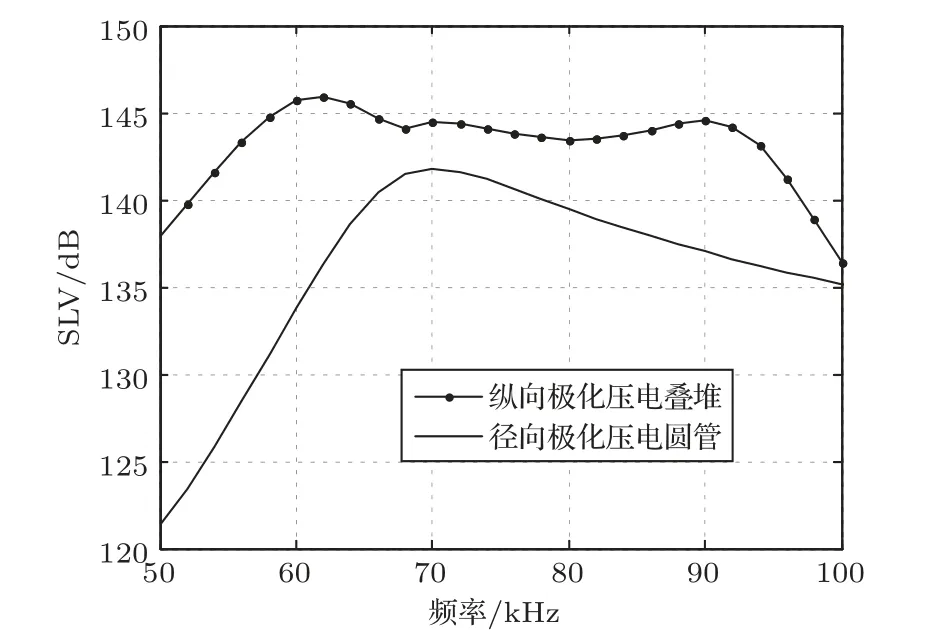
图10 压电管堆换能器发射电压仿真曲线Fig.10 The transmitting voltage response of the prototype model

3 样机制作与测试

3.1 换能器样机制作

为了保证换能器大功率下的发射特性，需要对压电管堆施加纵向预应力，由于换能器尺寸较小如采用传统预应力螺杆结构会对振动模态产生较大影响，为此设计了图11结构图中的环氧预应力层。首先利用外力装置对装配完成的压电管堆模块施加预应力，将加力后的压电管堆灌注环氧树脂，待环氧树脂固化形成包裹层后撤去外部施力装置，利用已固化的环氧包裹层保持施加的预应力。环氧树脂材料的声阻抗远低于压电陶瓷，可以最大程度降低预应力结构对换能器振动辐射特性的影响。

根据理论分析及仿真结果研制换能器样机，如图11所示压电陶瓷管堆外径17 mm，内径12 mm，高度16 mm，高径比约为2.2。换能器样机按照图11的结构图装配完成，主要结构包括安装法兰、去耦泡沫、管状压电叠堆、环氧预应力层、聚氨酯水密层等。为了减小安装法兰对换能器的影响，将压电陶瓷管堆安装在换能器前端1/4位置，中间部分采用去耦泡沫材料填充，封装后换能器直径25 mm，高100 mm。

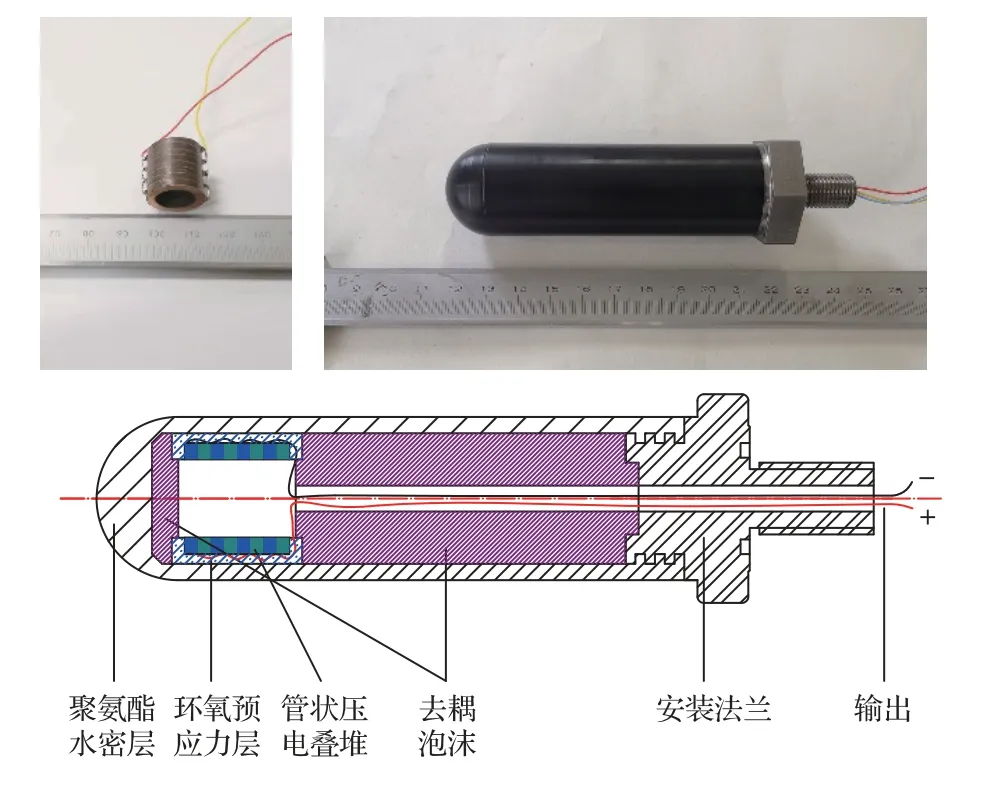
图11 换能器样机实物及结构图Fig.11 Photographs and sketch of the prototype

3.2 换能器样机测试分析

在中国科学院声学研究所消声水池测试了换能器样机的发射电压响应曲线和指向性。图12是换能器发射电压响应测试结果，可以看出换能器的低频谐振峰在55 kHz附近，响应约为145 dB，高频谐振峰在80 kHz附近，响应约为143.5 dB。两个模态的响应峰值基本相当，换能器-3 dB工作带宽为51～84 kHz。受到压电材料参数、结构参数等误差的影响，实测工作频带比仿真结果略低，发射电压响应幅度及宽带特性基本符合。

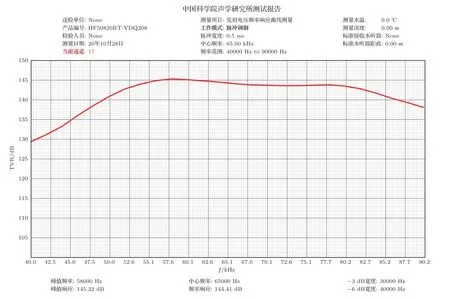
图12 换能器样机发射电压响应测试曲线Fig.12 The measured transmitting voltage response curve of the prototype

测试了换能器的大功率发射特性，具体结果如表1所示。在换能器两端施加980 V的峰峰值电压时，最大声源级达到195.6 dB，初步具备了较大功率的发射能力。换能器样机内陶瓷单元的厚度为2 mm，理论上可以施加1400 V左右的峰峰值电压。而实际测试中继续提高输入电压时标听的接收波形产生畸变，其原因可能是环氧树脂包裹层提供的预应力不足。受限于环氧材料较低的刚度，在此结构下很难进一步提高预应力，对于预应力结构的设计以及预应力层与压电管堆的刚度匹配等问题仍待进一步研究。

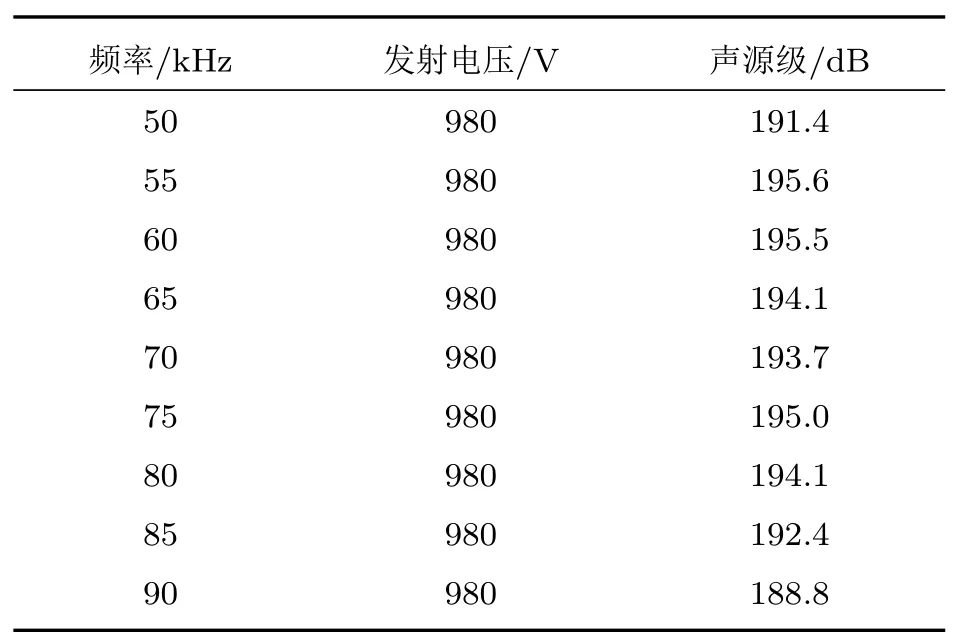
表1 换能器样机声源级测试结果Table 1 Tested source level of the prototype

4 结论

本文利用压电陶瓷管堆结构实现了一种纵向极化的圆管发射换能器，探讨利用管堆结构纵向与径向振动耦合实现宽带声辐射。研究了压电陶瓷管堆的振动耦合特性，用有限元方法对换能器进行建模仿真，分析换能器谐振频率、发射电压响应随高径比参数的变化规律，研制换能样机并进行测试。实测换能器最大发射电压响应达到145 dB，-3 dB工作带宽51～84 kHz与仿真结果基本符合。换能器最大声源级达到195 dB左右，初步具备了较大功率的发射能力。在大功率发射方面，换能器预应力结构的设计以及预应力层与压电管堆的刚度匹配等问题仍需要进一步研究。

压电管堆式宽带换能器借鉴了切向极化镶拼圆管的设计理念，利用压电陶瓷高效的纵向压电效应来提高换能器发射性能，具有比径向极化压电陶瓷圆管更高的响应特性和带宽特性。压电陶瓷管堆结构简单，适用于小体积高频圆柱形发射换能器的设计，在中高频段圆管换能器的设计中有一定的优势。此外，压电管堆式宽带换能器的阻抗特性可以通过压电单元的数量和极化厚度进行调整，进一步提高了设计自由度和适用性。