混凝土声发射信号源定位精度的细观模型计算分析*

黄逸群 孙岳阳王 洋胡少伟

(1福建工程学院土木工程学院 福州350118)

(2苏州科技大学土木工程学院 苏州215009)

(3武汉大学水利水电学院 武汉430000)

(4重庆大学土木工程学院 重庆400000)

0 引言

声发射是材料在产生变形或损伤时以弹性波形式释放应变能的自然现象。多数材料的声发射强度不高，人耳无法直接听到，需借助灵敏的电子仪器进行探测。

声发射技术作为一项新兴的无损、动态的检测技术，目前在混凝土材料断裂损伤机理的研究中已得到了广泛的应用：如运用混凝土破坏过程中的声发射基本参量或二次处理参量(能量、振铃计数、撞击数，RA值等)变化趋势表征来预测或判断混凝土的破坏程度[1-9]；结合混凝土受载破坏全过程的能量变化率建立相应的混凝土本构模型[10-11]；通过信号识别及处理，反演混凝土内部损伤[7-8]；通过声发射源的定位确定混凝土加载过程的内部裂缝开展路径[9]等。

相较于一般的均匀材料如金属、塑料，混凝土是一种由骨料、砂浆、骨料砂浆交界面、内部孔隙等组成的多相非均匀准脆性材料[12]。而由于目前声发射的定位计算方法假设声速在材料内匀速传播，因此混凝土内部的非均匀性决定了在对其进行声发射源定位时必然会出现一定的误差。对于误差的程度，目前的研究定性分析较多，定量分析较为罕见。为详细了解混凝土内细观因素对混凝土内部声发射源定位精度的影响，本文从细观尺度出发，基于混凝土细观结构与在遗传算法基础上实现的时差定位算法，定量计算分析了骨料含量、声速偏差对混凝土材料定位精度的影响。

1 计算模型

1.1 混凝土二维细观多边形骨料模型

混凝土常见的骨料形状多为带棱角的多面体，在细观力学问题中，采用多边形(多面体)而不是圆形(球)对骨料进行模拟更为符合实际情况。本文所采用的方法是对基础多边形进行扩充，生成复杂多边形，随后逐个将其投入指定区域，采用相应算法排除骨料重叠情况，最终生成骨料结构[13]，如图1所示。

图1 多边形骨料结构生成示意图Fig.1 The generation of polygon aggregates

1.2 基于遗传算法的声发射时差定位算法

时差定位算法是通过传感器接收到同一声发射信号的时间差，结合传感器布置位置，采用数学方法对声发射信号源进行定位的方法。其基本原理如图2所示，以二维问题为例，假定声发射信号源坐标为(x,y)，各声发射传感器的坐标为(xi,yi)，则声发射信号源到各声发射传感器的距离Si为

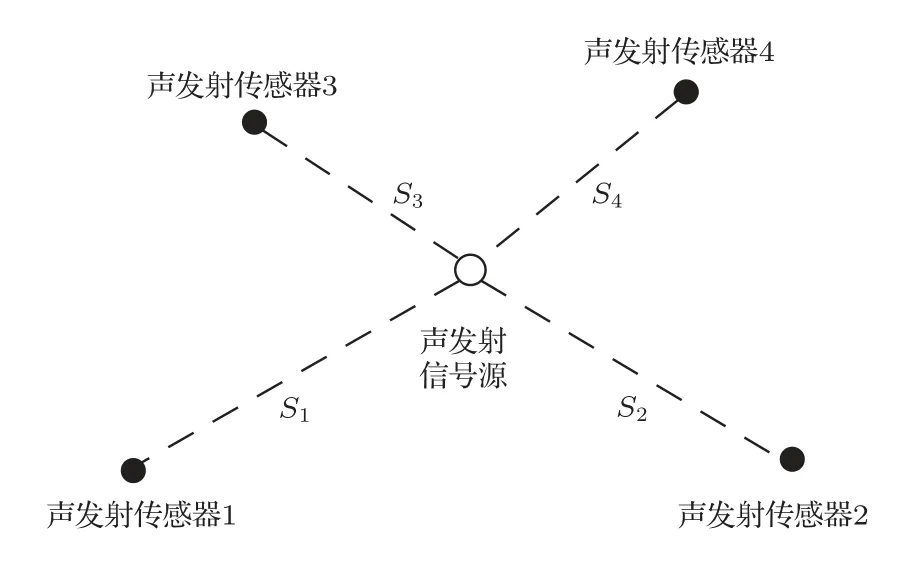
图2 声发射定位示意图Fig.2 Acoustic emission positioning diagram

定义第i个声发射传感器探测到某一声发射事件与声发射事件产生时的绝对时差为ti，则各声发射传感器之间测得的同一声发射事件的时间差Δtij为

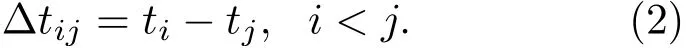
假设所测物内部为均匀介质，其声速为v，则各传感器测得同一声发射事件的时间差满足如下公式：

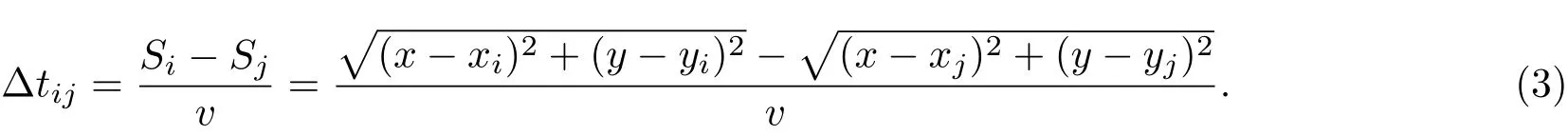
由式(3)可得

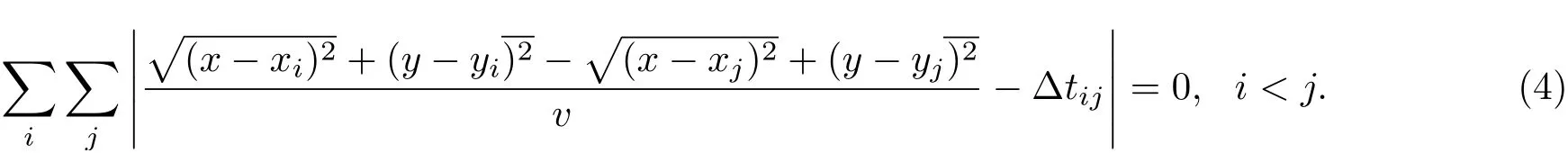
根据式(4)，在定位计算中，假定近似的声发射信号源坐标为(x*,y*)，定义χ2为

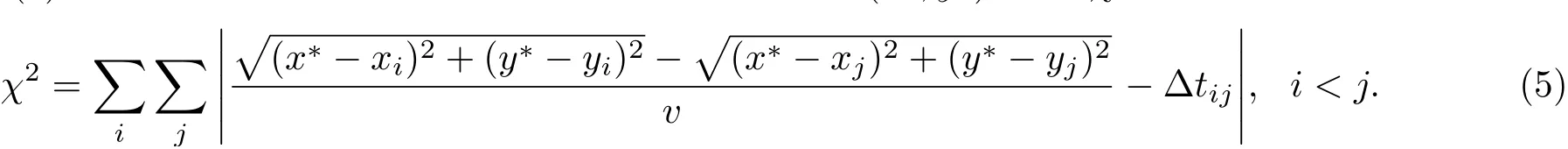
若计算得到的近似声发射信号源越接近实际声发射信号源，则有χ2越接近于零[14]。因此，基于声发射时差的信号源定位本质上是一个χ2最小值的求解问题，是一个典型的数学优化问题。

遗传算法是一种通用而有效的求解最优化问题的方法，适合用于寻找文中χ2的最小值。其基本原理为：首先产生一组初始解，这组初始解称为群体。群体中的每一个个体即为待优化问题的一个解，这些个体在后续的迭代中与较优的个体通过交叉及变异的运算方式产生下一代的个体，其称为后代。由于后代继承了上一代种群中的优点，因此整体性能要优于上一代种群。经过若干代的迭代之后，种群收敛于最好的个体，一般来说，该个体即为问题的最优解。

针对二维问题，本文采用遗传算法对声发射信号源定位的方法为

(1)在包含真实信号源的区域内产生一系列的个体，使其形成初始种群。其中每个个体的值为其中T为遗传代数，i为其所代表的个体编号，对于初始种群，T为1。

(2)根据式(5)计算当前种群中每个个体的χ2值，找出χ2值最小的个体，称之为最优个体，其值为

(3)将当前种群中所有个体与最优个体进行交叉及变异运算，得到下一代的种群。下一代种群的生成公式为

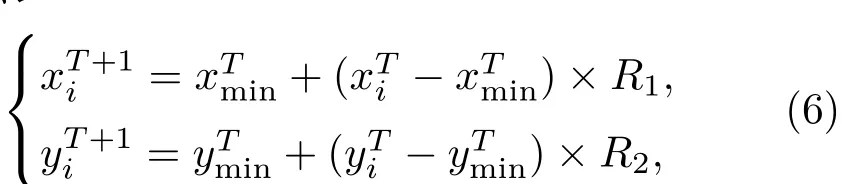
式(6)中，R1、R2为0～1的随机数。

(4)判断是否满足收敛条件，若不满足，返回步骤(2)继续迭代；若满足，则退出迭代，输出最后一代的优势个体，并以其为最优解。

图3给出了该定位方法的程序框图。

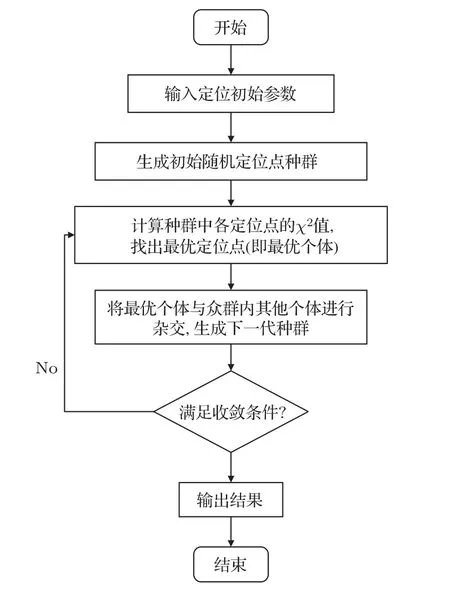
图3 定位算法的程序框图Fig.3 The algorism of positioning

1.3 声发射时差定位算法的可靠性验证

为了验证声发射定位算法的可靠性，本文进行了一组模拟实验。模拟试验如图4所示，声发射探头布置在0.3 m×0.3 m的均质正方形区域的4个顶点。假定该正方形区域内的声速为3000 m/s，区域内放置了一系列声发射信号源，这些信号源沿竖直方向呈正弦函数分布，由于声发射信号在该区域内匀速传播，各声发射探头测得的同一声发射事件的时间差为

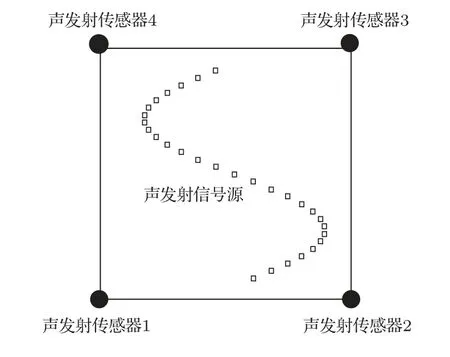
图4 声发射定位模拟试验示意图Fig.4 The arrangement of AE positioning simulation experiment

式(7)中：Si为第i个探头与声发射信号源的距离，v为该传播介质内的声速。

图5为计算后的声发射信号源与预设定声发射信号源的对比。可以看出，计算得到的声发射信号源与预设定信号源位置基本重合，通过误差分析，其平均误差距离约为0.03 mm，最大误差距离不超过0.1 mm，是该区域对角线长度的0.033%，表明在均质体内使用遗传算法对声发射源进行定位具有可行性。

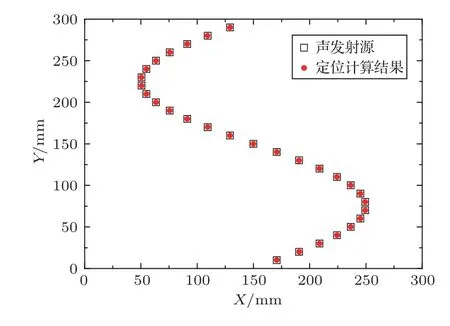
图5 声发射信号源定位模拟实验结果图Fig.5 The result of AE positioning simulation experiment

2 数值计算结果及分析

虽然混凝土在本质上是一种由骨料、砂浆以及骨料-砂浆交界层构成的三相模型，但由于骨料-砂浆交界层的厚度不超过100 μm[15]，远小于骨料和砂浆的尺寸，声发射信号在该区域传播时间极短，可不考虑其影响，因此在计算时将混凝土视作由砂浆以及骨料构成的二相模型。典型的混凝土二相模型如图6所示。

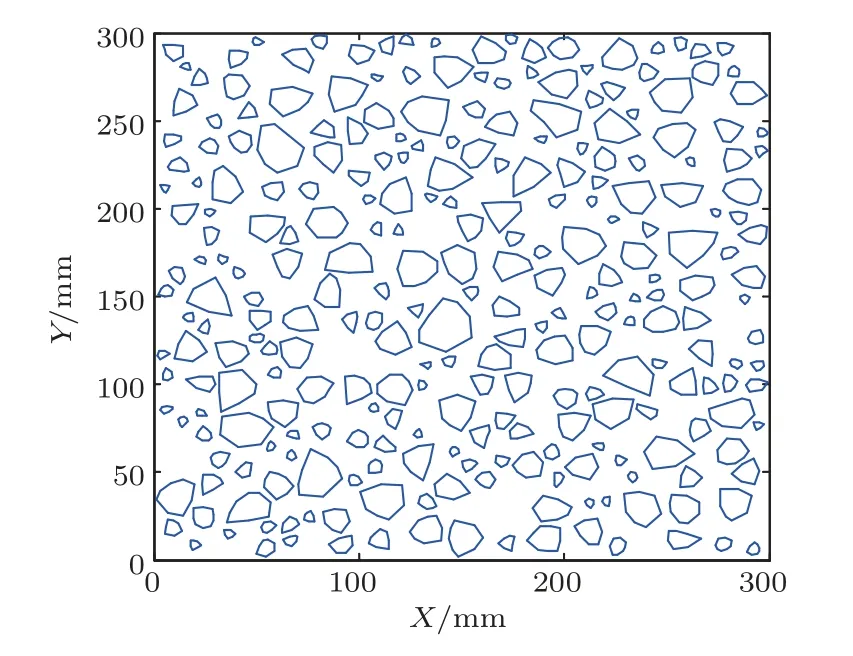
图6 混凝土二相模型示意图Fig.6 The concrete aggregate-mortar meso model

在进行模拟试验时，由于骨料与砂浆的声传播速度不同，声发射信号从信号源传播到声发射探头所需的时间需特别计算，在不考虑信号反射和折射的情况下，其计算方法如图7所示：首先将模拟信号源与探头位置相连，形成一条线段；然后分别统计该线段上通过骨料以及砂浆区域的长度；最后计算声发射信号从模拟信号源传至探头的时间，其计算公式如下：

图7 混凝土中声发射信号传播示意图Fig.7 Propagation of acoustic emission signal in concrete

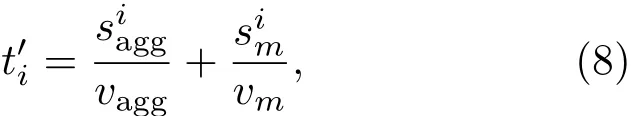
则各传感器测得的同一模拟声发射事件时间差为

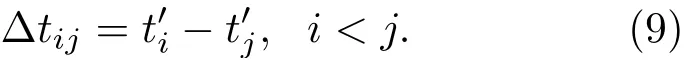
2.1 骨料含量对混凝土平均声速的影响

由于时差定位算法本质上是一种将被测物体设为均质物的计算方法，在计算时需首先提供被测物的平均声速。本节将对混凝土的平均声速通过模拟试验进行统计分析，首先应确定砂浆与骨料的声速取值。值得注意的是，根据文献[9]，混凝土的波速在传播距离超过200～300 mm后会出现一个明显的衰减，这是由于速度较快的纵波在传播距离较大时幅值会大幅衰减，从而导致在距离较大时传感器只能接收到横波信号，而无法接收到纵波信号。由于本文中后续的测试区域尺寸均在300 mm以内(实际试验时测试区域的大小通常也与这一尺寸相当[1-3])，因此，文中主要使用纵波的时间差用以定位。根据弹性力学[16]，固体的波速(纵波)可采用如下公式计算：

式(10)中：v为固体内纵波波速，E为该固体弹性模量，ρ为其密度。

根据文献[15,17–18]，骨料及砂浆的基本材料参数取值如表1所示。

表1 混凝土各组分材料参数Table 1 Material parameters of concrete components

已知混凝土声发射信号从信号源传播至传感器所需的时间可通过式(8)求得，根据图7，则易得混凝土中平均声速的计算公式为

为了探究不同骨料含量对混凝土平均声速的影响，进行了6组0.3 m×0.3 m的试件的平均声速统计试验。每组试验有3个试件，用以消除离散性。试件形式如图8所示，骨料含量(空间占比)分别为20%、25%、30%、35%、40%、45%，骨料粒径范围在5～31.5 mm，符合连续级配。

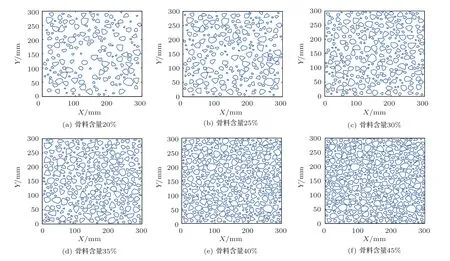
图8 不同骨料含量的试件Fig.8 The specimens with different aggregate content

为了更好地表现区域内声速的分布规律，在上述试件内沿水平、竖直方向均匀布置81个理想声发射信号源，这些信号源的信号规律被假设为完全一致，且在信号传播过程中不考虑其能量衰减以及折射反射。此外，还在试件的4个顶点放置4个传感器，如图9所示。

图9 声发射模拟信号源及探头布置Fig.9 The arrangement of AE analog signal source and AE sensors

通过计算，不同骨料含量的平均混凝土声速值统计分析如图10所示。随着骨料含量的增加，混凝土内部平均声速随之线性增长，但各测试点统计而得到的声速差异系数(波速标准差/波速平均值)基本不变，表明骨料含量只对平均声速有影响，对混凝土内部材料的均匀性影响不大。

图10 骨料含量对平均声速的影响Fig.10 The impact of aggregate content on average wave velocity

2.2 混凝土骨料含量对声发射信号定位精度的影响

为了探究不同骨料含量对混凝土内部信号源定位精度的影响，进行了6组0.3 m×0.3 m的试件的平均声速模拟统计试验，其中骨料的体积含量分别为20%、25%、30%、35%、40%、45%，每组试验有3个试件，试件形式如图8所示。信号源及探头的布置同图9所示。定位计算时采用之前已通过计算得到的不同骨料含量的声速，典型的计算结果如图11所示，蓝点为信号源的位置，红点为定位计算得到的位置。可以看出，由于混凝土内部有砂浆和骨料两种不同传播介质，导致声波从声发射信号源到各探头的传播速度不一致，而定位计算时采用的是平均声速，必然导致了定位上的偏差，因此使得混凝土这种非均匀介质的声发射信号源定位的效果不如均匀介质的定位效果。

骨料含量对定位误差的影响如图12所示，图中纵坐标的含义为定位计算结果与实际信号源之间的距离，声发射源的定位的绝对误差值基本不受骨料含量的影响。模拟结果表明，在骨料含量的正常变化范围内，骨料含量并不会对混凝土内部的均质性以及相应的定位精度产生太大的影响。

图12 混凝土定位误差与骨料含量关系图Fig.12 The impact of aggregate content on positioning error

2.3 声速取值偏差对定位的影响

在实际对混凝土进行声发射定位时，由于一些客观因素，平均声速的取值往往会存在一定的偏差。为了分析声速取值偏差对定位的影响，采用0.3 m×0.3 m的测试区域，骨料含量为30%，根据之前的计算得到的平均声速，取基准声速为3748 m/s，对定位计算时采用的声速进行-20%、-10%、0、+10%、+20%的偏差化处理，简单研究了声速取值偏差对定位误差的影响，计算结果如图13(a)～(e)所示。可以看出，相较于细观骨料的因素，声速的取值偏差对定位误差的影响十分明显，当声速取值小于平均声速，定位得到的结果整体往区域中心集中；而当声速取值大于平均声速时，定位结果整体向外部扩散，且声发射源越靠外侧，误差显现的越明显。图13(f)为定位绝对误差(平均值)与声速取值偏差的关系图，结果表明定位误差与声速偏差基本呈线性关系，且声速取值偏差对定位的影响在测试区域的边缘处远超材料不均匀性。

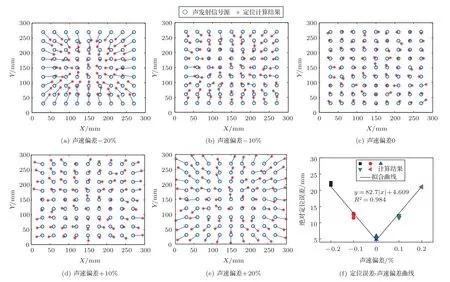
图13 声速偏差对声发射源定位的影响Fig.13 The impact of wave velocity deviation on AE positioning

3 结论

本文基于多边形骨料细观混凝土结构以及遗传算法，对混凝土声发射定位精度开展了定量的分析和研究，主要得到了以下结果及结论：

(1)建立了一种混凝土声发射定位误差计算模型，该模型可用于定量的分析并评估细观结构及计算参数对定位精度的影响，相较于传统的经验判断更为清晰直观。

(2)基于所建立的计算模型，定量研究了骨料含量及声速取值偏差对定位精度的影响，得出：1○在正常的骨料含量变化范围内，混凝土的骨料含量对定位精度基本不产生影响；2○相较于细观的因素，声速取值偏差对定位结果造成的偏移程度远大与细观构造对定位结果的影响。

基于以上结论，可以得出，在实际使用声发射对混凝土内信号源定位时，应通过调整探头的布置，尽可能地使潜在的声发射信号源处于测试区域的中心，使其到各探头的距离偏差不要过大，从而减小因声速取值导致的定位误差。

此外，值得指出的是，本文所进行的研究是在二维理想情况下进行的，而实际情况下混凝土是三维结构。因此，后续相应三维计算模型的建立以及与实际试验结果对比的分析研究仍有待进一步开展。