直接辐射式扬声器系统的低频效率计算公式*

陈睿 沈勇 冯雪磊

(南京大学声学研究所 近代声学教育部重点实验室 南京210093)

0 引言

很多便携式产品(如便携式音箱、手机)要求扬声器系统轻便、小巧的同时，具有更长的工作时间[1]，因此更高的电声转换效率是扬声器系统设计和优化的重要目标[2]。目前，扬声器系统在电声转换时会有较大损失，其效率仅为0.2%～2%[3-4]，已成为相关产品提升工作时间的短板弱项。

扬声器系统的效率是设计和优化扬声器系统的重要指标，可以用于分析扬声器系统各个参数对效率的影响，并寻求最优参数，实现效率的提升。现有的研究通常根据TS参数计算扬声器系统的标称效率，相关公式由Small[5]给出。然而，标称效率将扬声器系统的电阻抗视为音圈的直流电阻，对于阻抗变化较大的低频并不适用[6-7]，制约了扬声器系统低频效率的优化提升。Keele[8-9]提出“真实”效率的定义，对比了不同Bl值的扬声器系统的标称效率和“真实”效率。利用“真实”效率的定义，可以计算扬声器系统的低频效率，相较于标称效率，低频效率具有更广适用范围，能更清晰地揭示各个参数对效率的影响，更有利于扬声器系统效率优化提升。本文的研究对象是采用动圈式扬声器单元的直接辐射式扬声器系统，旨在基于TS参数，提出封闭式扬声器系统和倒相式扬声器系统低频效率的计算公式，并进行实验验证。

1 低频效率的计算方法

本文的研究对象是采用动圈式扬声器单元的直接辐射式扬声器系统，它一般包含扬声器单元、腔体、倒相管或无源辐射体以及泄漏等部分。考虑各个部分的声阻抗以及电阻抗，可以画出直接辐射式扬声器系统的声学类比线路图和电学类比线路图，如图1所示[5]。图1(a)、图1(b)中各参数的含义分别如表1、表2所示。图1(a)中的电流表示体积速度，通过求出扬声器系统所有向外辐射声能的部位的体积速度之和，可计算扬声器系统的输出声功率；利用图1(b)中的电学类比线路图求其总电阻抗，可进一步计算扬声器系统的输入电功率。其他相关参数为：ρ0：空气密度；c0：空气中的声速；f：声波频率，对应角频率ω=2πf；s=jω：复频率；k：声波波数；a：扬声器单元等效半径；扬声器单元共振频率，并令ωs=2πfs，Ts=1/ωs；Qes=2πfsCmesRe：扬声器单元的电学品质因数；Qms=2πfsCmesRes：扬声器单元的机械品质因数；Qts=1/(1/Qes+1/Qms)：扬声器单元的总品质因数；τ=Qms/Qes：扬声器单元的机械品质因数和电学品质因数之比；α=Cas/Cab：扬声器系统声顺比。

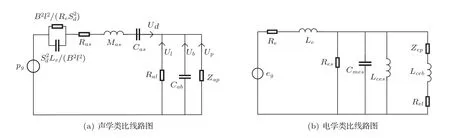
图1 直接辐射式扬声器系统的声学、电学类比线路图Fig.1 Acoustic and electrical analog circuit of the direct-radiator loudspeaker system

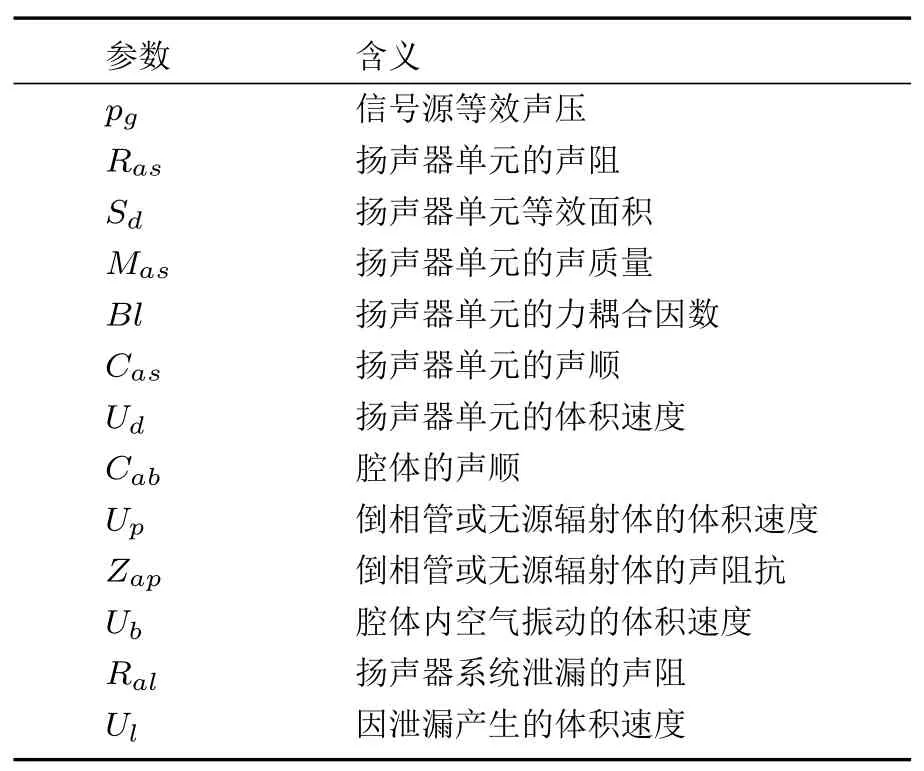
表1 图1(a)中参数的含义Table 1 Meaning of parameters in Fig.1(a)

表2 图1(b)中参数的含义Table 2 Meaning of parameters in Fig.1(b)

1.1 标称效率和低频效率

扬声器系统的效率η是输出声功率WA和输入电功率WE的比值[5]，即

对于输出声功率WA，直接辐射式扬声器系统的总辐射声功率包含扬声器单元、倒相管(或无源辐射体)和泄露辐射的声功率，因此可得[5]

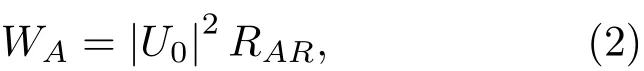
其中，RAR为扬声器单元的辐射声阻，U0=Ud+Ul+Up为向外辐射声能的3部分的体积速度之和[5]。在低频，即ka≪1，3个部分可视为在同一位置处的点声源，令p(r)为半空间中距离扬声器系统r处的声压有效值，利用点声源的声压计算公式，有[10]

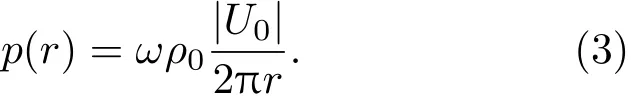
由此半空间的辐射声功率表示为

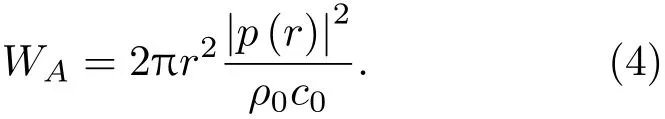
在计算标称效率时，假定扬声器系统的电阻抗可视为扬声器单元音圈的直流电阻，此时输入电功率为

将式(4)代入式(1)，并将WE,N替代式(1)中的WE，经过推导可以得到标称效率ηN为[5]

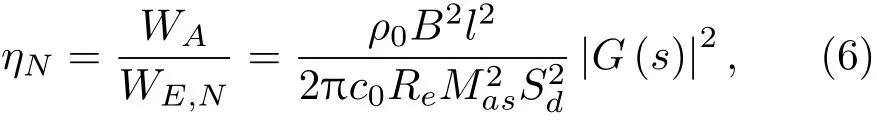
ηN由两部分组成，其中G(s)=sMasU0/pg[5]，是扬声器系统的响应函数；系数称为参考效率，是一个与频率无关的常数，用η0表示[5,11]。

实际上，扬声器系统的总电阻抗|ZE|并非常数，而是一个随频率变化的值。在扬声器系统的质量控制区，|ZE|接近常数，而在低频，|ZE|与Re有较大的区别，因此WE,N适用的频率范围有限[7]。低频段作用在扬声器系统上的有功功率WE,L为[8]

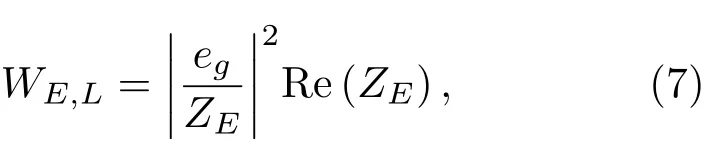
其中，Re表示取实部。因此，将式(4)代入式(1)，并将式(7)中的WE,L代入式(1)中的WE，可以得到低频效率ηL为

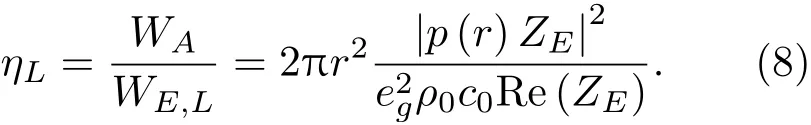
1.2 基于TS参数的低频效率计算公式

在低频段，扬声器单元电感的感抗ωLe很小，因此可以忽略电感。令Zes=1(1/Res+sCmes+Ras+sMas+1/sCas)、Zaa=RalZap/(Ral+Zap)，此时电阻抗Ze和声压p(r)分别为

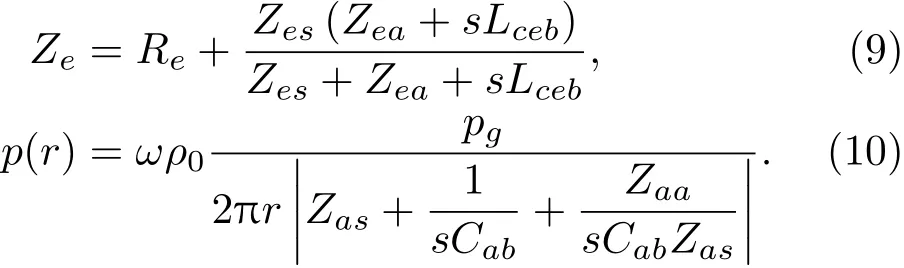
将式(9)和式(10)带入到式(8)，可得到标称的表达式为

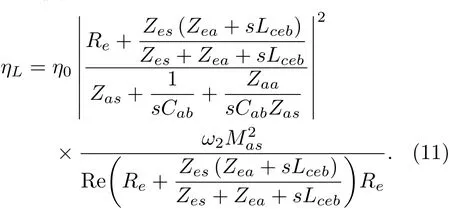
封闭式扬声器系统和倒相式扬声器系统均属于直接辐射式扬声器系统，接下来计算它们的低频效率公式。

1.2.1 封闭式扬声器系统

封闭式扬声器系统(以下简称为封闭箱)不包括倒相管或无源辐射体等部件，所以Zap→∞，

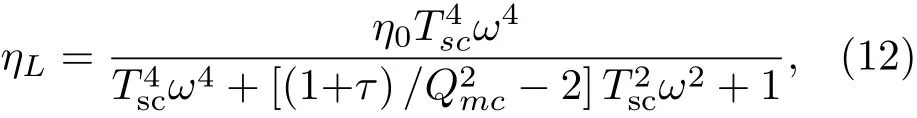
1.2.2倒相式扬声器系统

对于倒相式扬声器系统(以下简称为倒相箱)，忽略倒相管内的声能损耗，其声阻抗和对应电阻抗分别为Zap=sMap，Zep=1/sCmep。令表示后腔和倒相管的共振频率；令Ql=1/2πfbRelCmep，表示倒相箱的泄漏损耗品质因数；令h=fb/fs，表示调谐比；令表示中心频率。利用公式(11)计算得到倒相箱的低频效率为

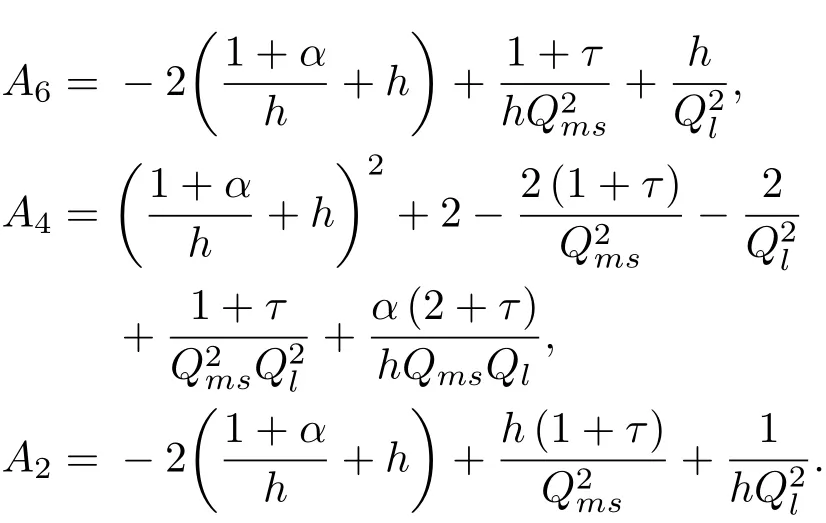
其中，令Ql→∞，可以去掉系数中与Ql有关的所有项，此时的式(13)为不考虑泄漏时倒相箱的低频效率。

2 实验验证

为验证本文提出的基于TS参数的低频效率计算公式，分别设计制作了两个封闭箱(封闭箱A和封闭箱B)和两个倒相箱(倒相箱A和倒相箱B)，其中封闭箱A采用扬声器单元1，封闭箱B采用扬声器单元2，倒相箱A和倒相箱B均采用扬声器单元3。4个扬声器系统如图2所示。

图2 四款扬声器系统的照片Fig.2 Photos of four loudspeaker systems

实验对比分析低频效率的理论值和实验值，首先采用Klippel电声测量仪测量扬声器系统的阻抗和TS参数，分别采用式(12)和式(13)计算得到低频效率的理论值，然后测量扬声器系统的轴向频率响应，采用式(8)得到低频效率的测量值。为对比低频效率和标称效率的区别，采用式(6)得到标称效率的理论值，采用式(4)和式(5)得到标称效率的测量值。4个扬声器系统的部分参数测量值如表3所列。

表3 实验用扬声器系统的部分参数Table 3 Partial parameters of the loudspeaker systems used in the experiments

对于轴向频率响应，实验在南京大学消声室进行，通过B&K PULSE声频分析仪馈给扬声器系统测量信号并分析传声器的测量数据，传声器(B&K 4191)距离扬声器系统1 m，测量频率范围为20～1000 Hz，扬声器系统的输入电压为0.5 V。

四款扬声器系统低频效率的理论值和实测值如图3所示。由图3可见，低频效率的理论值和实测值较为符合，20～300 Hz范围内的平均效率的相对误差分别为封闭箱A 8.47%，封闭箱B 6.7%，倒相箱A 2.81%，倒相箱B 4.26%。

为对比封闭箱和倒相箱低频效率和标称效率的区别，图3中也给出了标称效率的理论以及实测曲线。从图3(a)、图3(b)中可以看出，对于封闭箱，随着频率提升，低频效率曲线很快上升，在扬声器系统fsc附近达到最高值，随后快速下降并逐渐趋于平直，在低于400 Hz的低频段，封闭箱低频效率明显高于标称效率。从图3(c)、图3(d)可以看出，对于倒相箱，随着频率提升，倒相箱的低频效率曲线总体呈快速上升趋势并达到最高值，但期间有可能短暂下降并出现一个极大值(例如倒相箱A)，随后便和封闭箱一样，快速下降并逐渐趋于平直，在低于400 Hz的低频段，倒相箱低频效率明显高于标称效率。从对图3的分析中可以看出，标称效率与低频效率在低频段有着较大的差异。

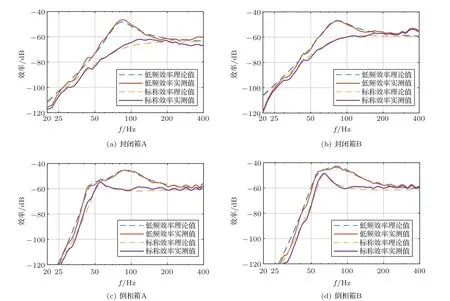
图3 扬声器系统效率理论值和实测值的对比Fig.3 Comparison between theoretical and measured values of loudspeaker system efficiency

3 分析与讨论

3.1 低频效率与标称效率的关系

对于标称效率和低频效率的关系为

对于封闭箱，在其共振频率fsc处，转换函数有最大值，两种效率的差别很大，例如图4(a)中封闭箱A在fsc处的低频效率达标称效率的11.8倍；对于倒相箱，转换函数在低频段有两个极大值，例如图4(d)中低频效率可达到标称效率的5倍以上。当频率逐渐升高，效率转换函数的值趋近于1，低频效率与标称效率的区别不再明显。此外值得注意的是，由于|ZE|≥Re，|ZE|≥Re(ZE)，效率转换函数的值恒大于等于1，也就是说直接辐射式扬声器系统的低频效率恒大于或等于标称效率。

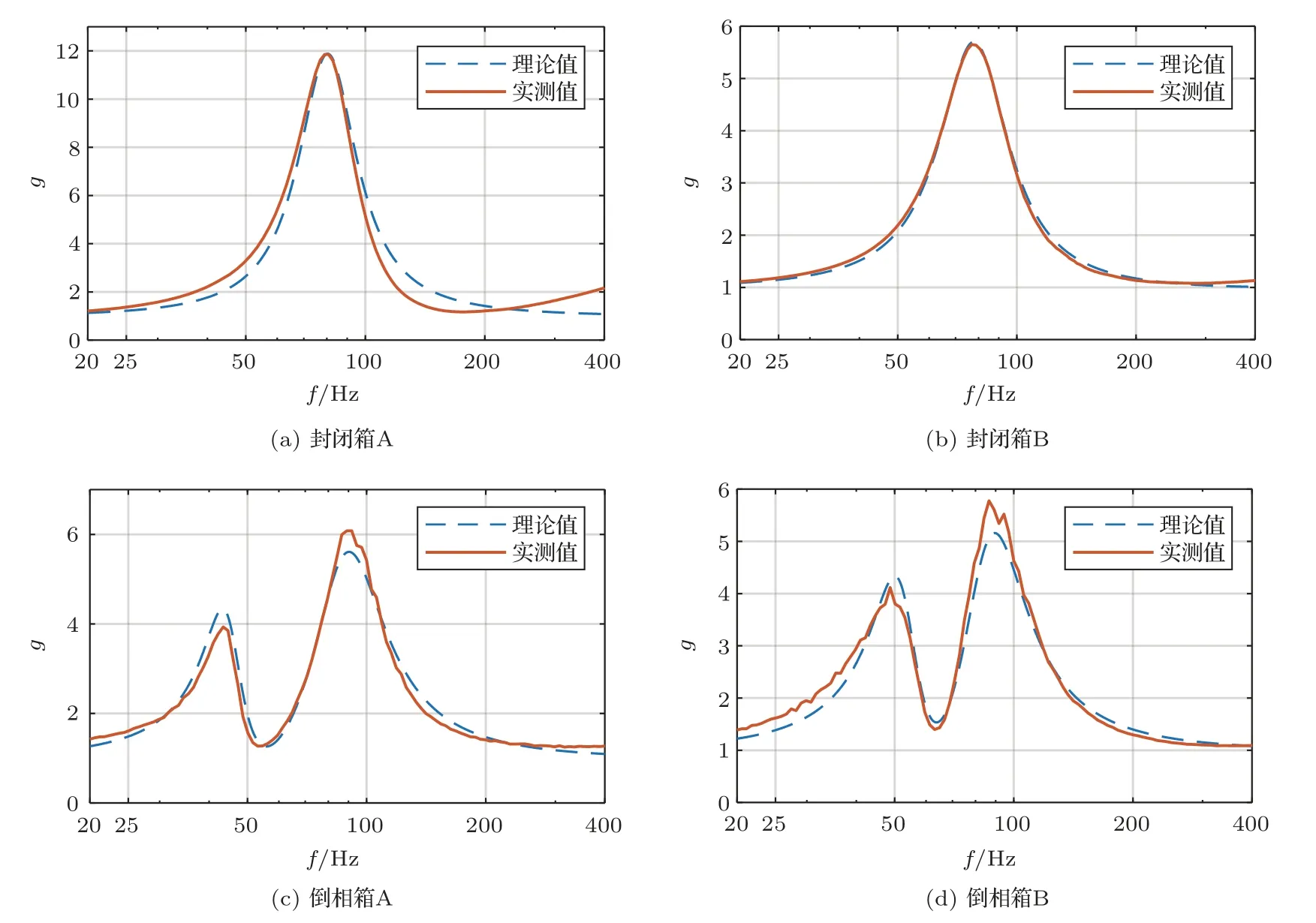
图4 四款扬声器系统的效率转换函数Fig.4 Efficiency conversion functions of four loudspeaker systems

3.2 低频效率的优势

信号源传递给扬声器系统的电功率由输入电压和扬声器系统电阻抗决定，扬声器系统的电阻抗值不仅与Re有关，还与扬声器系统的其他参数有关，是个随频率变化而变化的值。在低频，扬声器系统电阻抗值的变化很大，对于封闭箱，电阻抗曲线在共振频率fsc处出现一个峰[12]，对于倒相箱，则会出现两个峰[13]，峰值都远大于Re，当频率逐渐升高，到达中频的质量控制区，电阻抗值才逐渐趋近于常数，因此利用式(5)中WE,N计算得到的标称效率η0仅代表质量控制区的效率[14]。式(7)中的WE,L计算了信号源实际作用在扬声器系统上的有功功率，考虑了扬声器系统电阻抗随频率变化的特点，所以利用WE,L计算得到的低频效率ηL不仅适用于质量控制区，也能够适用于低频。

由于具有更广的适用范围，相比标称效率，低频效率能准确、直观地反映扬声器系统参数值对其效率的影响情况。以参数Re为例，保持其他参数不变，改变表3中的封闭箱A和倒相箱A的Re值，分别观察其低频效率和标称效率的变化情况，如图5所示。图5(a)中标有1、2、3的曲线对应的Re值分别为1.7 Ω、3.3 Ω、6.6 Ω，其他参数均未改变；图5(b)中标有1、2、3的曲线对应的Re值分别为2.8 Ω、5.6 Ω、11.2 Ω，其他参数均未改变。

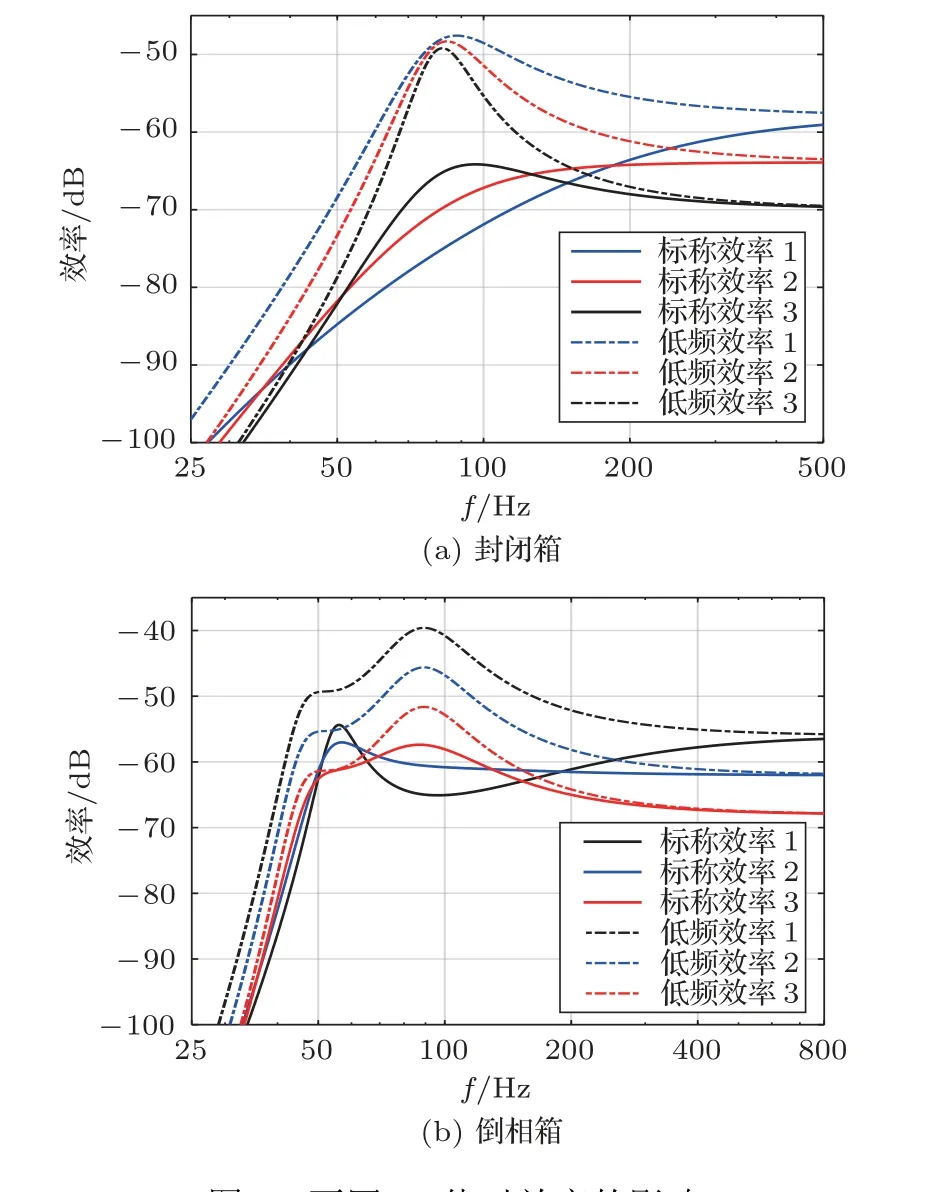
图5 不同Re值对效率的影响Fig.5 Effect of different values of the Re on efficiency

从图5可以看出，两种效率与Re值的关系有所不同，对于Re更小的扬声器系统，标称效率在部分频段更高，在部分频段更低，低频效率则在整个频段都会更高。实际上，低频效率曲线在整个中低频段都准确、直观地反映了Re对效率的影响，而标称效率在低频段是不适用的，因此在需要提高扬声器系统效率时，设计者不需要因为顾忌部分低频段标称效率的下降而不选择低Re值的扬声器系统。

4 结论与展望

本文从电学和声学类比线路图出发，针对封闭箱和倒相箱，给出了基于TS参数的低频效率计算公式，并通过实验验证了理论公式的正确性。进一步分析了低频效率与标称效率，结果表明低频效率恒大于等于标称效率，并且低频效率具有使用范围更广、更加直观的优势。本文提出的计算公式，可以在扬声器系统及相关产品的设计阶段，便捷快速地得到低频效率，有助于提升和优化扬声器系统及相关产品的声学性能。