机体表面湍流边界层噪声特性及预测方法研究

宋 晓Cyrille Breard孙一峰 田嘉劲

(上海飞机设计研究院 上海201210)

0 引言

飞机作为一种快捷高效的交通工具，其客舱舒适度日益受到人们的关注。对于民用飞机的舒适性而言，主要目的是保持客舱内较小的噪声水平。巡航阶段是整个飞行过程中时间最长、对乘客舒适性影响最大的阶段。随着大涵道比发动机的广泛应用，发动机噪声有所降低，湍流边界层噪声已成为巡航过程中最主要的外部噪声源。

飞机机体表面的流动受边界层外的潜在流动所驱动，流动会在机体表面产生压力脉动，压力脉动只局限于边界层内。边界层的流动开始于层流，但很快就会变为湍流，因此，机身的边界层大部分是湍流。边界层内的压力脉动被称为湍流边界层噪声。湍流边界层噪声通过复杂的传递路径进入舱内，会激发结构振动和噪声。一般而言，湍流边界层噪声对舱内噪声的贡献主要集中在中高频范围，主导了舱内400 Hz～2 kHz的噪声场[1]。湍流边界层内的压力脉动可以被看作一个随机过程，可用统计学的方法来描述。对于湍流边界层噪声的预测，目前主要是基于半经验的方法，其中包括频率-波数谱模型和描述局部压力波动的单点谱模型。关于单点谱模型，国外学者通过大量的实验数据拟合出了多种工程模型。Robertson[2]根据Lowson[3]的研究成果和NASA的试验数据建立了Robertson模型，随后Cockburn & Robertson[4]对其表达式进行了改写，发展出Cockburn & Robertson模型。Chase[5]建立了Chase模型，Howe[6]在其基础上对模型进行了简化，发展出Chase-Howe模型。Goody[7]根据多个实验研究结果对Chase-Howe模型进行了修正，发展出Goody模型。Efimtsov等[8-9]建立了Efimtsov1模型和Efimtsov2模型。

关于湍流边界噪声的研究，国外已经进行了相关的飞行试验[10-11]，而国内针对这方面的研究还很少。本文通过开展飞行试验获取了某型飞机的机体表面压力脉动。结合试验数据与定常流动计算，分析了高度、速度、压力梯度等参数对湍流边界噪声的影响。最后利用Robertson模型、Cockburn&Robertson模型对湍流边界层噪声进行了预测，分析了预测结果与试验结果的差异，并根据试验数据对预测模型的参数进行了优化，提高了湍流边界层噪声的预测精度，为湍流边界层噪声的预测提供了工程依据。

1 飞行试验

飞机的前后机身和翼身整流罩区域共布置9个表面传声器，其中传声器型号为BK4948。各个测点的具体分布如图1所示。表面传声器采用过渡圆盘的方式进行安装，通过铝箔胶带和双面胶将其固定于机身表面，与传声器相连的线缆在机身表面顺气流方向布置，最终通过改装后的舷窗进入客舱内部，与数据采集系统连接。

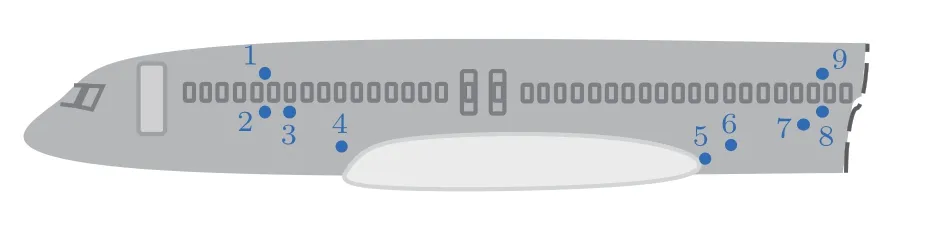
图1 传声器布置示意图Fig.1 Microphone layout

湍流边界层噪声与飞行高度和飞行速度有密切关系，因此，试验点主要选取不同高度、不同速度的巡航工况，见表1。巡航工况下发动机按需调整转速。考虑到当地声速会随高度变化，对工况2～工况4的马赫数进行一定的调整，使其接近于恒定的真空速，以便进行直接比较。调整后，工况2和工况3的真空速一致，工况4与工况2、工况3有2%左右的偏差，就其对噪声水平的影响而言，此偏差是可以接受的。在整个试飞过程中，巡航工况至少保持30 s。

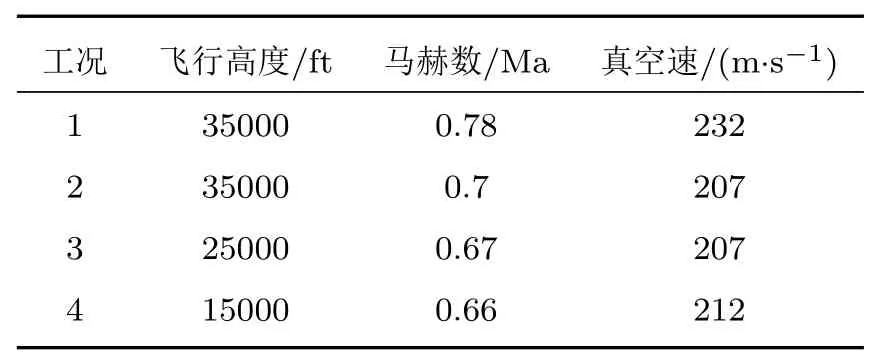
表1 试验工况Table 1 Test conditions

2 试验数据分析

2.1 发动机噪声的影响

飞机机体表面的压力脉动主要包括发动机噪声和湍流边界层噪声。其中，相同的飞行高度、飞行速度下，发动机噪声主要受发动机转速影响。为了分析测点处的噪声水平是否受到发动机噪声的影响，对相同飞行高度和速度、不同转速下的测点噪声进行分析。图2为试飞中工况2的稳定的过程，可以看出，在t1时刻和t2时刻，飞行高度、速度基本一致，而发动机转速分别为60%和80%。

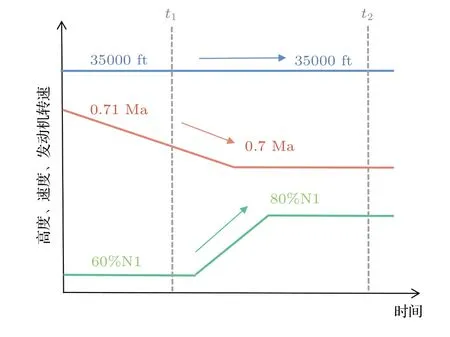
图2 工况2稳定过程Fig.2 Stability process of Condition 2

对t1时刻和t2时刻各测点处的噪声谱进行对比，发现发动机转速变化后，除4号测点外，其余测点的噪声谱基本不变。因此，除4号测点外，其他测点处的湍流边界层噪声淹没了发动机噪声。图3为4号测点t1时刻和t2时刻的噪声谱对比，可以看出4号测点在发动机高转速下有一个明显的900 Hz左右的纯音，该纯音为发动机风扇叶片通过频率噪声，而宽带噪声谱基本重合。该点距离发动机风扇较近，风扇前传噪声中宽带被湍流边界层噪声淹没，但是风扇叶片通过频率噪声较为突出，无法被湍流边界层噪声淹没。其他工况下，发动机噪声对测点噪声的影响规律是一致的。因此，当前试飞工况下，发动机噪声仅对4号测点处的噪声有影响，叠加了一个发动机纯音噪声，而发动机噪声对其他测点的噪声没有影响，实测的单点谱可以被认为是湍流边界层噪声的频谱特征。

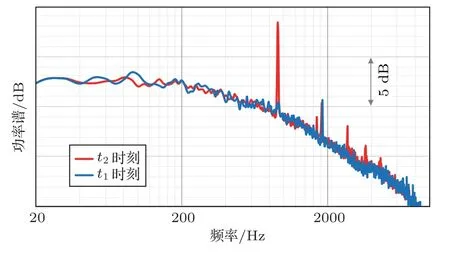
图3 t1和t2时刻测点2的压力脉动Fig.3 The fluctuation pressure of Point 2 at time t1 and t2

2.2 高度和速度的影响

研究表明湍流边界层噪声的幅值与动压和壁面剪切应力有关[12-16]。其中，以动压为自变量的壁面压力脉动均方值半经验公式如下：

式(1)中，q=1/2ρU2为来流动压，ρ为密度，U为速度，a为常数。

从式(1)可以看出，飞行速度越大、高度越低(空气密度越大)，则动压越大，进而湍流边界层噪声越大。图4显示了飞行高度和飞行速度变化对2号测点处噪声的影响。可以看出，飞行高度降低10000 ft会导致湍流边界层噪声增加3 dB左右，飞行马赫数从0.7增加到0.78，湍流边界层噪声会增加2 dB左右。表2为根据式(1)估算的湍流边界层噪声变化量，可以看出计算的结果与实测结果基本一致。

表2 湍流边界层噪声变化量Table 2 Variation of turbulent boundary layer noise

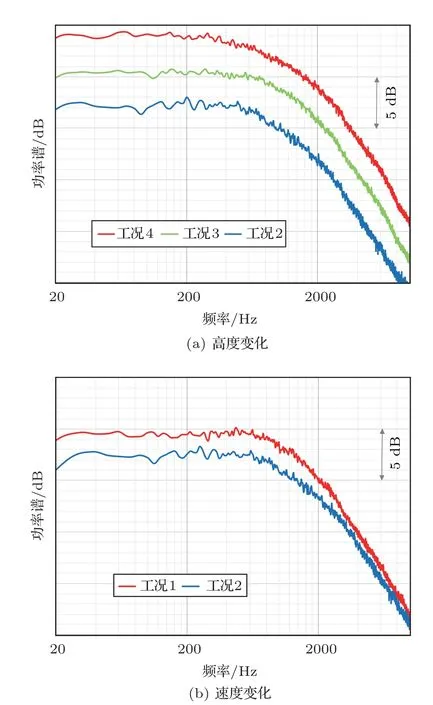
图4 不同工况测点2的压力脉动对比Fig.4 The fluctuation pressure of Point 2 at different conditions

2.3 位置的影响

图5为工况2下前机身和后机身区域6个测点的噪声谱，可以看出前机身区域3个测点的噪声谱基本重合，这也是符合预期的，因为前机身区域3个测点距离机头的距离差异较小，局部边界层厚度变化不大。同样地，后机身区域3个测点的噪声谱基本重合也是因为其局部边界层厚度相近。对比前后机身区域的噪声谱可以看出，低频范围内后机身区域测点的幅值较前机身区域明显增加，这反映了边界层的发展，距离机头越远边界层越厚，因此，湍流边界层内较大的拟序结构在频谱中占有优势。需要指出，其他工况下前后机身区域的噪声谱也具有相似的规律。

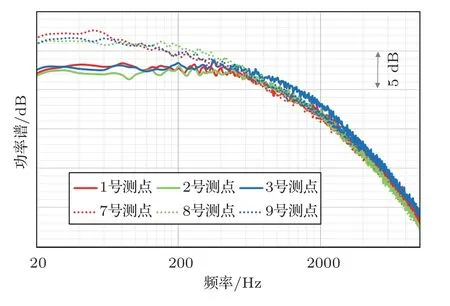
图5 工况2下前后机身不同位置的压力脉动对比Fig.5 The fluctuation pressure of front and rear fuselage at Condition 2

2.4 压力梯度的影响

逆压梯度会诱导边界层分离，对湍流边界层噪声有一定的影响。通过定常流动计算可以得到机身表面的压力系数，识别并量化出压力梯度明显变化的区域。图6为工况2下的机身表面压力系数。可以看出，机身周围的流动十分复杂，有着明显的加速和减速现象，这可能影响到湍流边界层噪声的频谱特性。前后机身区域的6个测点都不在压力梯度区内，如前所述，前后机身区域内各个测点的声压级有着很好的一致性。

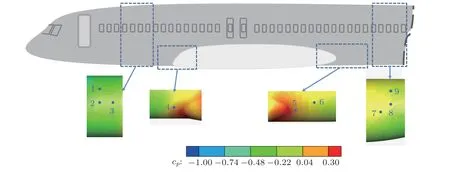
图6 机身压力系数分布Fig.6 Fuselage pressure coefficient distribution

图7为工况2下翼身整流罩区域5号、6号测点以及后机身区域7号测点的噪声谱对比。靠近翼身整流罩的5号测点噪声幅值明显大于其他测点。从图6可以看出，5号测点处于逆压梯度区，其噪声增大与局部分离有关。6号测点相比5号测点离翼身整流罩较远，受逆压梯度影响较小，其频谱特性与后机身区域7号测点的频谱基本一致。

图7 工况2下5～7号测点的压力脉动对比Fig.7 The fluctuation pressure of Point 5–7 at Condition 2

图8为工况2下翼身整流罩区域4号测点与前机身区域3号测点的噪声谱对比，其中3号测点的噪声谱去除了发动机纯音噪声。可以看出，在200～2000 Hz范围内，4号测点的幅值比3号测点小1～2 dB。考虑到两个测点处的边界层厚度差别不大，因此，该差异可能与顺压梯度有关，但从整体上来看，顺压梯度对湍流边界层噪声的影响较小。

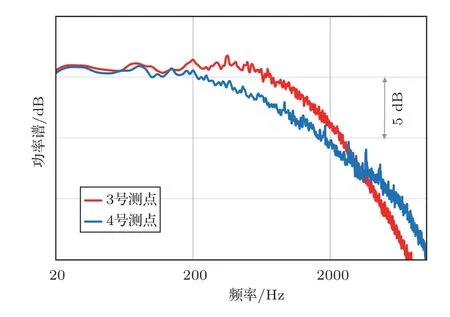
图8 工况2下3号和4号测点的压力脉动对比Fig.8 The fluctuation pressure of Point 3–4 at Condition 2

3 湍流边界层噪声工程预测

3.1 单点谱模型

湍流边界层噪声的单点谱模型有基于飞行试验发展形成的，也有基于风洞试验发展形成的。不同单点谱模型的频谱形式不同。本文通过真实飞机飞行试验，发现Robertson模型和Cockburn &Robertson模型对于民机的湍流边界层噪声预测适用性较好。

关于Robertson模型，文献[2]指出，在Ma为0.6～3的范围内，Robertson模型计算的湍流边界层单点噪声与实验数据符合较好。Robertson模型的表达式如下：

式(2)中，ω0为特征频率，p′2为压力脉动均方值，

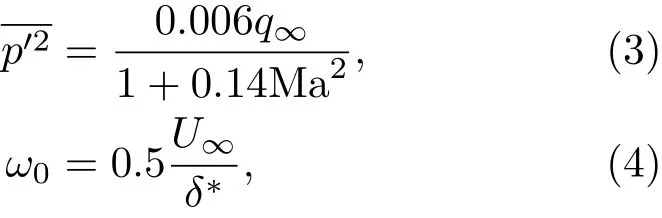
其中，Ma为来流马赫数，U∞为来流速度，δ*为边界层位移厚度，q∞为来流动压。

Cockburn&Robertson对Robertson模型的特征频率进行了改写，发展的Cockburn & Robertson模型表达式如下[4]：

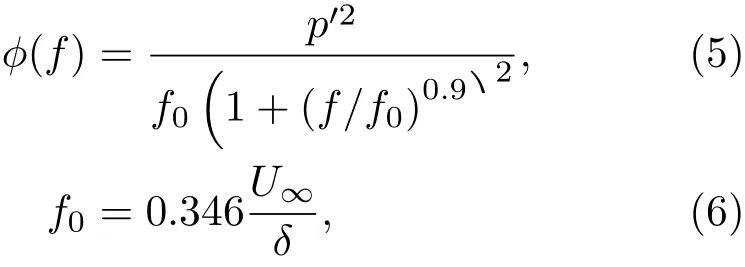
其中，特征频率f0采用边界层厚度δ作为自变量，而不是位移边界层厚度δ*。

对于平板湍流边界层的厚度，可以由式(7)～(8)估算[17]：

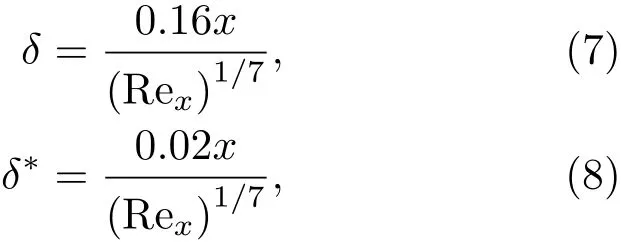
其中，x为平板长度，Rex为基于平板长度的雷诺数。

根据式(7)、式(8)可知δ=8δ*。因此，可以将Robertson模型和Cockburn&Robertson模型写成统一的形式，如下：

其中，A、B、C为常数。对于Robertson模型，相应的参数A=0.9，B=2，C=0.6366。对于Cockburn& Robertson模型，相应的参数A=0.9，B=2，C=0.346。两者的差异仅在于参数C的取值。

式(9)中A、B、C三个参数的取值决定了整个频谱的形态。图9为参数变化对预测结果的影响，选取工况2条件下2号测点处的飞行参数作为计算输入。从图9中可以看出，参数C主要影响曲线的低频区域，C值越小，预测的低频幅值越大。Cockburn& Robertson模型预测的低频噪声大于Robertson模型主要在于选取了较小的C值。参数B主要影响曲线的高频区域，B值越大，高频衰减越快。而参数A主要控制频谱的形态，A值越大，曲线弯曲越明显。

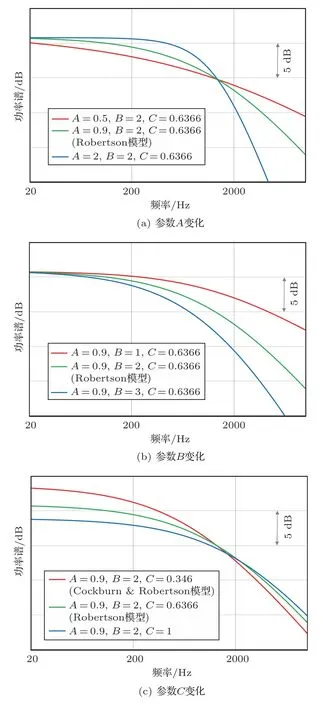
图9 参数变化的影响Fig.9 Influence of parameters change

3.2 预测结果分析

图10为工况2下测点2和测点8处的试验值和预测值的对比，其中边界层厚度通过式(7)、式(8)确定。可以看出，Robertson模型和Cockburn& Robertson模型的预测结果与试验结果基本吻合，其中差异较大的频段有2 dB左右偏差。对于200 Hz以下的预测，Robertson模型相比Cockburn & Robertson模型与试验值吻合更好，说明参数C取0.6366对于本文的研究较为适用。基于Robertson模型的预测值与试验值的偏差集中在200～2000 Hz，主要在于Robertson模型所计算的频谱弯曲程度低于试验结果，表明参数A的默认取值偏小。

图10 工况2下试验值和预测值对比Fig.10 Comparison of test value and predictive value at Condition 2

为了优化Robertson模型中的参数，保持参数C=0.6366不变，通过最小二乘法得到新的参数A值、B值，见表3、表4。可以看出，基于试验数据拟合的A值、B值和Robertson模型中的默认值有一定的差异。本文选取A=2、B=1对湍流边界层噪声进行重新预测，如图11所示。可以看出，对于前后机身区域的测点，在各个工况下预测值和试验值基本上重合，相比原始的Robertson模型预测结果有明显改善。

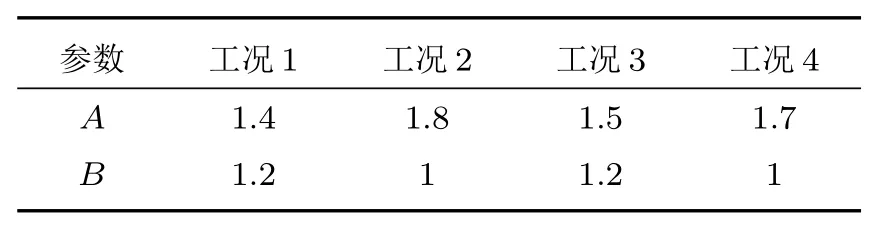
表4 最小二乘法求A、B(基于8号测点)Table 4 Calculating parameter A and B by least square method(based on Point 8)

图11 试验值和优化后的预测结果对比Fig.11 Comparison of test value and optimized prediction result

表3 最小二乘法求A、B(基于2号测点)Table 3 Calculating parameter A and B by least square method(based on Point 2)

4 结论

本文对某型民机巡航阶段的机体表面压力脉动进行了分析。机身表面的压力脉动主要由湍流边界层噪声贡献，在前后机身区域，发动机噪声完全淹没在湍流边界层噪声中。湍流边界层噪声的幅值与动压呈正相关。边界层厚度对湍流边界层噪声的影响主要在低频区域，边界层越厚，低频噪声越大。逆压梯度会使边界层噪声变大，而顺压梯度的影响较小。基于Robertson模型计算得到的湍流边界层噪声与试验结果吻合较好，对模型中的参数进行优化，可以进一步减小预测结果和试验结果的差异。