应对说话人位置突变的鲁棒语声去混响*

吴礼福 孙帅恒王 雷孙芯年

(1南京信息工程大学电子与信息工程学院 南京210044)

(2江苏省大气环境与装备技术协同创新中心 南京210044)

0 引言

由于墙壁、地板或天花板的反射，在封闭空间(如会议室)采集的语声信号将不可避免地包含混响[1]。混响会降低语声信号的清晰度和质量，影响自动语声识别和助听器系统的性能[2-3]。混响语声信号由直达声(Direct sound)、早期反射(Early reflection)和晚期混响(Late reverberation)三部分组成。直达声是不经反射，直接从声源发出被传声器收集到的声音；紧随直达声音的，被称作早期反射，它通常由反射次数较少的强反射构成；最后一部分是由一系列难以区分的反射构成，称作晚期混响[4]。早期的反射分量并不会引起混响效应，反而会增强语声的清晰度。因此，晚期反射分量是混响效应中造成语声感知质量下降的主要原因。“去混响”(Dereverberation)的目的就是在保留语声直达分量和早期反射分量的同时，减少所获取信号中的晚期混响分量。

Lebart等[5]提出了一种基于谱增强的单通道语声去混响技术，并由Habets[6]将其推广到多通道去混响算法中，然而，谱增强法通常会出现由相位和幅度估计误差所引起的语声失真。多通道线性预测(Multi-channel liner prediction,MCLP)算法是一种常用的基于语声线性预测模型的去混响方法，能够在有效衰减混响的同时保证语声质量。Nakatani等[7-8]在基于MCLP算法的基础上，结合语声信号的时变特性，提出了基于统计模型的语声去混响方法，即加权预测误差(Weighted prediction error,WPE)算法。WPE算法可以在时域或短时傅里叶变换(Short time Fourier transform,STFT)域中进行，但是WPE算法是离线的批处理算法，不能实现实时地自适应去混响[9]。

在线的自适应去混响算法可以基于递归最小二乘(Recursive least squares,RLS)算法[10]实现。自适应去混响算法在保证具有快速收敛率的同时，还需准确地更新滤波器系数。然而，在实际的会议系统中，当话者切换导致说话人位置突变时，房间冲激响应(Room impulse response,RIR)也会随之改变，如果在已收敛的滤波器系数之后继续更新滤波器系数，算法存在发散的风险或者需要较长的收敛时间[11]。本文在自适应去混响算法的基础上，集成了一种对说话人位置突变的检测方法，可以较为准确地判断说话人位置是否突变，当检测到说话人位置发生变化时，通过初始化滤波器系数以提高算法的稳定性和收敛速度。

1 基于RLS的MCLP去混响方法

1.1 MCLP去混响算法模型

传声器阵列模型如图1所示，假设房间里仅有一个声源，利用均匀线性传声器阵列进行语声信号采集，共有M个远场传声器。

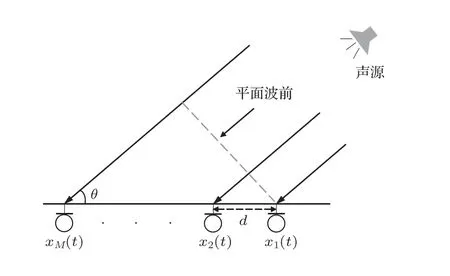
图1 传声器阵列模型Fig.1 Microphone array model

MCLP算法在时域建模时，预测滤波器的长度设置与RIR的长度呈正相关。在混响时间较长时，预测滤波器的长度会非常长，导致求解滤波器系数的计算量很大。为了降低计算量，MCLP算法更多地选择在子带或STFT域进行建模[12]。本文采用STFT后的时-频域来表示声信号。设xm(n,k)为时-频域中第m个传声器在第n帧第k个频带处的观测信号，可以将其分解为期望信号dm(n,k)和后期混响rm(n,k)，

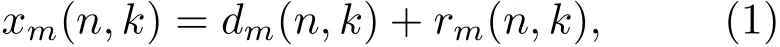
其中，dm(n,k)包含直达信号及其早期反射信号。

本文的目标是消除后期混响成分rm(n,k)，从而达到提取期望信号dm(n,k)的目的。根据文献[7]中提出的延迟线性预测模型，后期混响rm(n,k)可以从过去的观测信号中估计为

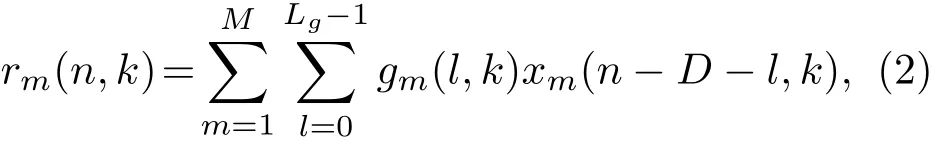
其中，gm(l,k)是第m个传声器在第k个频带处的第l个预测滤波器系数，Lg为预测滤波器的长度，D是在MCLP模型中引入的一个额外的预测延迟，以防止对语声信号的短时相关性造成明显的失真，达到只抑制晚期混响的目的，D的取值一般对应于时域中的10～30 ms，本文中设置为D=3(对应时域的24 ms)。结合式(1)和式(2)，期望信号dm(n,k)可以用矩阵形式表示为

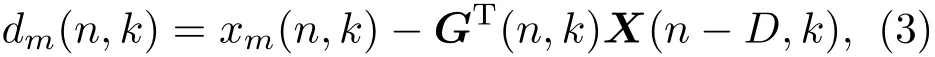
其中，预测滤波器的系数G(n,k)和语声信号X(n-D,k)都是一个大小为MLg×1的列向量，

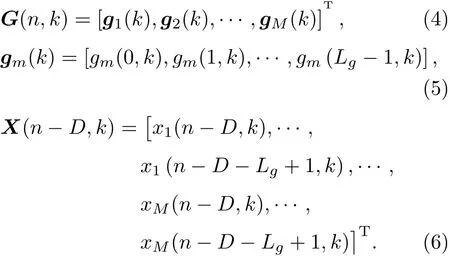
期望信号dm(n,k)可以看作延时线性预测模型中的预测误差，因此，通过计算预测滤波器在每一帧的每一个频点k处的预测系数G(n,k)，然后应用式(3)来实现最优滤波，达到语声信号去混响的目的。

1.2 基于RLS的自适应语声去混响算法

根据文献[9]，基于加权递归最小二乘(Weighted recursive least squares,WRLS)准则，求解时变的滤波器系数G(n,k)的代价函数可以定义为

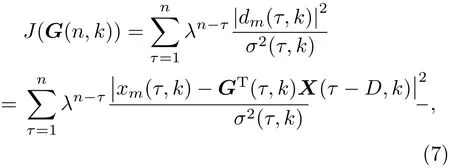
式(7)中的λ为遗忘因子，取值范围为0＜λ＜1。σ2(τ,k)为加权因子，是期望信号的方差。

令

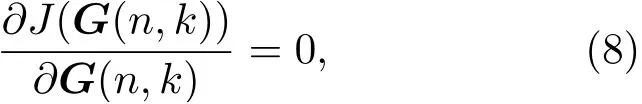
得到

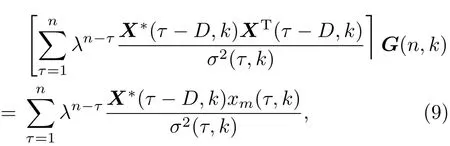
再令式(9)中

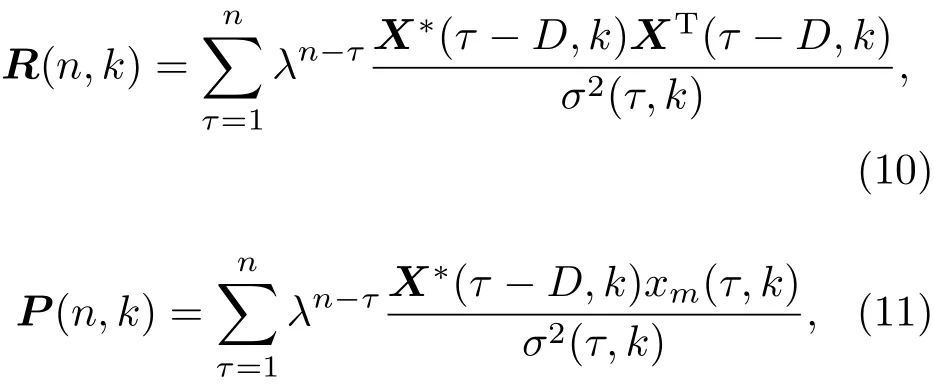
其中，符号(·)*表示对矩阵取复共轭。

联立式(9)～(11)可求得自适应滤波器系数G(n,k)的表达式为

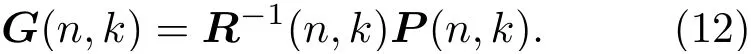
直接采用式(10)求解会涉及到对矩阵求逆的问题，即求解R-1(n,k)，因此，本文采用递推算法来迭代计算逆矩阵，利用Woodbury求逆公式[13]得到如下基于RLS的自适应去混响算法：

K(n,k)=

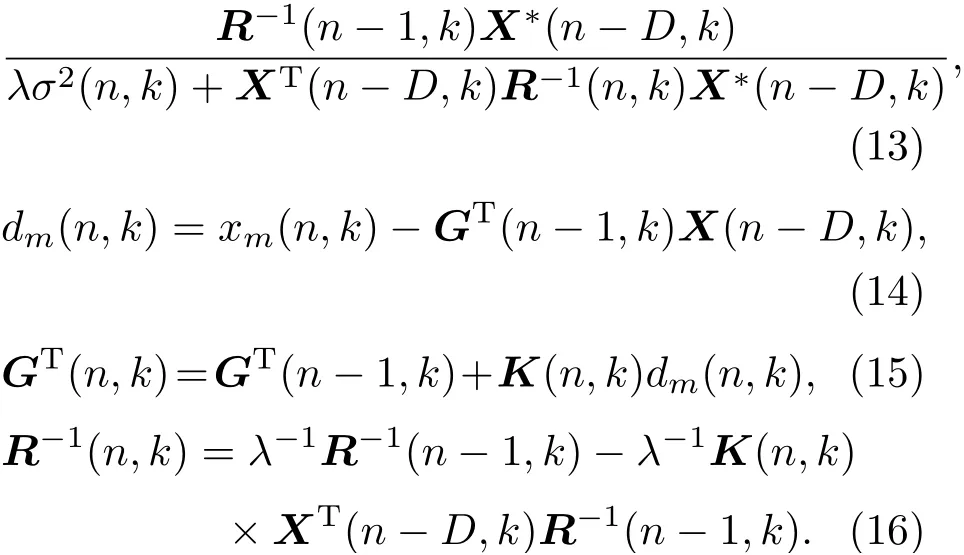
自适应算法根据式(13)～(16)对观测信号进行迭代计算，实现去混响。其中，期望信号的方差σ2(n,k)通过递归平滑的方式估计为

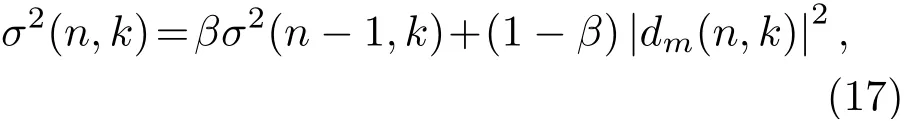
其中，β为递归平滑因子。

2 说话人位置变化检测方法

虽然第1节中描述的自适应去混响方法能够跟踪RIR的缓慢变化，但话者切换或说话人位置突变引起的RIR突然变化会使算法发散或者需要较长时间的迭代收敛。因此，为了更快速地跟踪RIR的突然变化，去混响算法最好能检测到说话人位置的突变，并重新初始化滤波器系数的更新。

基于MCLP的自适应去混响算法在对语声信号去混响后，依然保留了声源与传声器阵列之间的到达时间差(Time difference of arrival,TDOA)信息。当声源位置发生突变后，传声器阵元间的TDOA也必然发生变化。因此，可以对去混响信号进行时延估计(Time delay estimation,TDE)，通过检测不同传声器信号之间时延的变化来判断说话人位置的突变。

本文采用广义互相关(Generalized cross correlation,GCC)算法[14]来估计时延。将多路去混响信号作为时延估计算法的输入信号，根据式(18)得出当前帧的去混响信号之间的互相关函数，然后通过式(19)估计出去混响信号之间的时延：

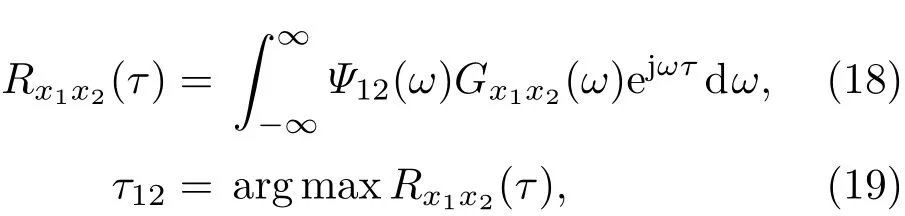
其中，Gx1x2(ω)为两信号之间的互功率谱，表示为为频域加权函数，表示为Ψ12(ω)=1/|Gx1x2(ω)|。这种加权函数被称为相位变换(Phase transformation,PHAT)加权，PHAT-GCC方法相对其他加权方法而言，对混响的鲁棒性较好[15]。

然而经过去混响后的语声仍会残留一些混响，这会导致时延估计算法在某些时刻产生错误的估计值，特别是当处于混响较强的环境下时，时延估计的正确率会明显降低，估计误差明显增大，这会影响对声源位置突变的判断。为了减少错误的时延估计值，提高算法的鲁棒性，对估计出的时延数据进行了下列处理：

(1)设置合理的时延区间

根据图1中的传声器阵列模型进行TDOA估计时，声源到传声器阵列的夹角为θ，d为两个传声器之间的间距，c为空气中的声速，根据传声器阵列的几何关系，两个传声器间的时延可以表示为τ12=dcosθ/c，因此正确的时延值应该满足

根据式(20)对估计的时延数值逐一进行判断，将不合理的时延剔除。

(2)数据平滑后取多帧平均

依次对每一帧的时延值进行数据平滑，平滑后的时延表示为

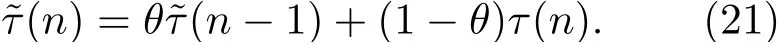
再对每m0帧的数据取均值，这m0帧时间内的时延表示为

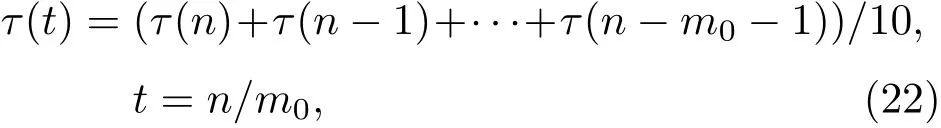
其中，m0的取值过大或过小都会影响算法的效果，本文通过实验验证选取了较为合适的数值，m0的取值为10。

(3)计算时延的相对变化

在每个时刻时延的相对变化定义为

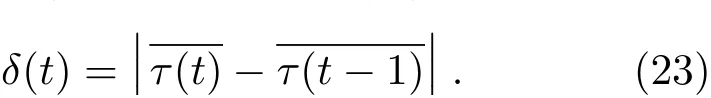
本文设定了一个阈值ϵ，若当前时刻时延的相对变化量大于设定的阈值，即满足δ(t)＞ϵ，则判定说话人位置发生突变。阈值ϵ的确定取决于时延的相对变化，而影响时延的相对变化量的主要参数是传声器间距d和声源角度θ，传声器间距d越大，选取的阈值ϵ也应该越大。针对本文的实验条件，为了选取一个合适的阈值，在第3节中进行了大量的仿真实验，最终根据仿真结果确定了ϵ的取值，见表1。

3 仿真实验

3.1 仿真环境

本文的仿真实验条件如下：利用Allen等[16]所提出的镜像源法(Image method)模拟生成RIR，模拟的房间尺寸为6 m×5 m×3 m，混响时间T60∈{300,500,800}ms。设置由4个传声器组成的线性阵列，其中传声器之间的间隔为10 cm，声源与传声器阵列中心的距离为2 m。声源先位于传声器阵列的左侧45°方向发声，6 s后改变到右侧45°的位置。仿真实验中的语声数据均来源于TIMIT语声数据库[17]，其采样频率为16 kHz。实验中的各项参数设置如表1所示。

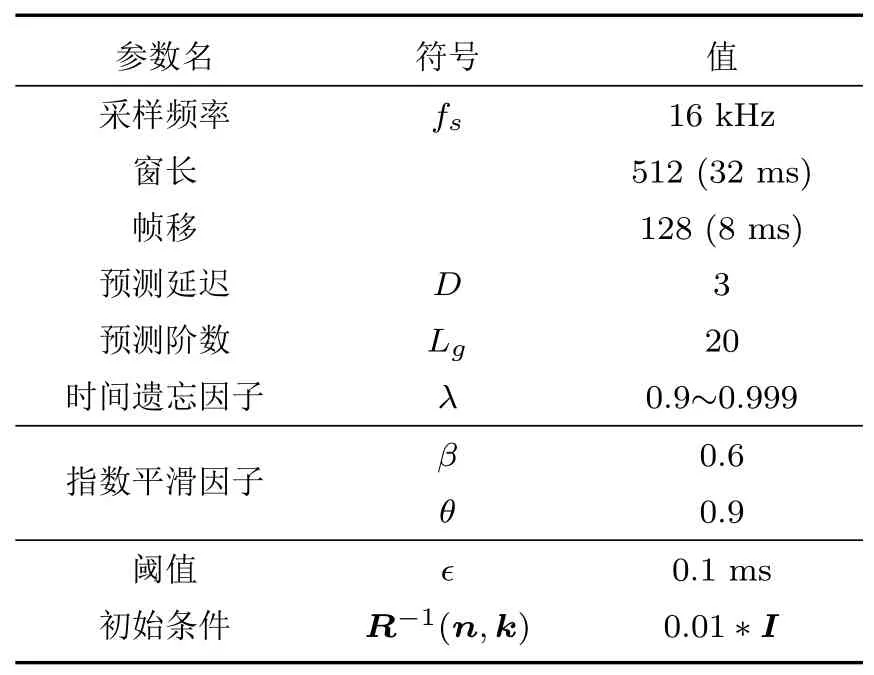
表1 实验参数设置Table 1 Experimental parameter setting

3.2 仿真结果

图2显示了混响时间T60=500 ms条件下时延的相对变化量，从图中可以看出，在6 s时刻说话人位置突变时，时延的相对变化量明显增大，超过了所设置的阈值。在大量的仿真测试中，第2节所提出的检测方法都正确地检测到了说话人位置的突变。

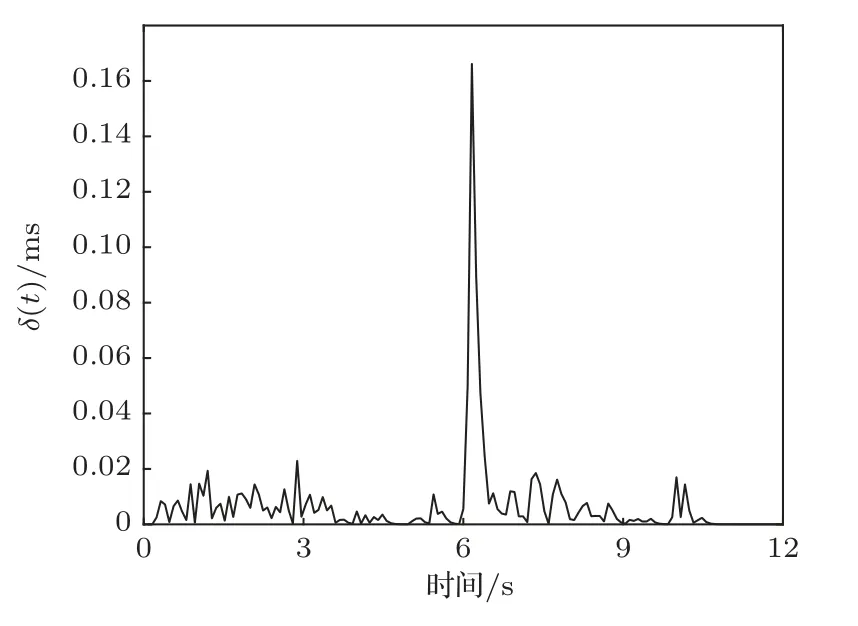
图2 时延的相对变化Fig.2 Relative variation of time delay

算法的性能和去混响效果采用Mel频率倒谱系数(Mel frequency cepstral coefficient,MFCC)距离改善(ΔMFCC)[18]和语声质量感知评价[19](Perceptual evaluation of speech quality,PESQ)两种客观指标来评估。最终的仿真结果均是10组不同模拟混响样本的集合平均值。

3.2.1 遗忘因子选择

为了确定最佳的遗忘因子大小，本文通过仿真验证了不同遗忘因子下算法的去混响性能，如图3所示。从图中可以看出，过小的遗忘因子会严重影响算法的去混响效果，这是因为遗忘因子过小会导致自适应算法在迭代过程中产生晚期混响过估计的问题，过多的消减掉了期望信号中的有用的语声信号成分，从而导致语声信号失真，因此应选择较大的遗忘因子。通过仿真验证，最终确定遗忘因子λ=0.995。

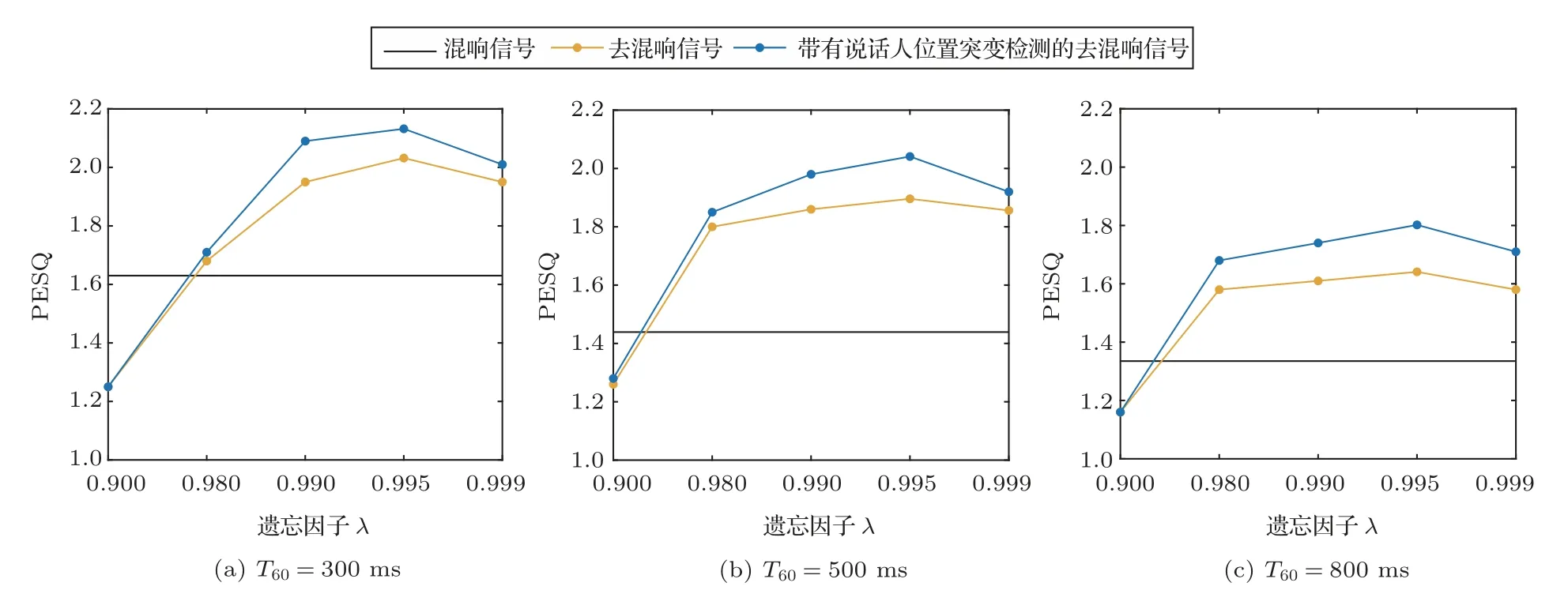
图3 不同遗忘因子下的PESQ得分Fig.3 PESQ scores under different forgetting factors

3.2.2 混响抑制性能分析

MFCC是一种优良的谱包络参数，MFCC在一定程度上模拟了人耳的听觉特性，所以基于MFCC的失真测度可以准确地体现出去混响语声的失真大小。把纯净语声作为参考信号，分别计算参考信号与混响信号和去混响信号之间的MFCC失真距离，记作MFCCin和MFCCout，然后两者做差便得到ΔMFCC，该值越大时，说明去混响效果越好。

从图4(a)中可以看出，在6 s时刻说话人位置突变后，ΔMFCC的值急剧下降，并且在1 s后才重新趋于稳定，这说明说话人位置的突变影响了算法的稳定性和去混响效果。图4(b)显示了具有说话人位置突变检测的去混响信号的ΔMFCC情况。相较于图4(a)，可以明显看出，6 s后图4(b)中ΔMFCC的值更快速地趋于稳定。这是因为具有说话人位置突变检测的RLS去混响算法在6 s时成功检测到说话人的位置变化，然后算法重新初始化滤波器的更新，提高了算法的收敛速度，获得了更好的去混响效果。这说明具有说话人位置突变检测的去混响算法有效提高了算法的鲁棒性。

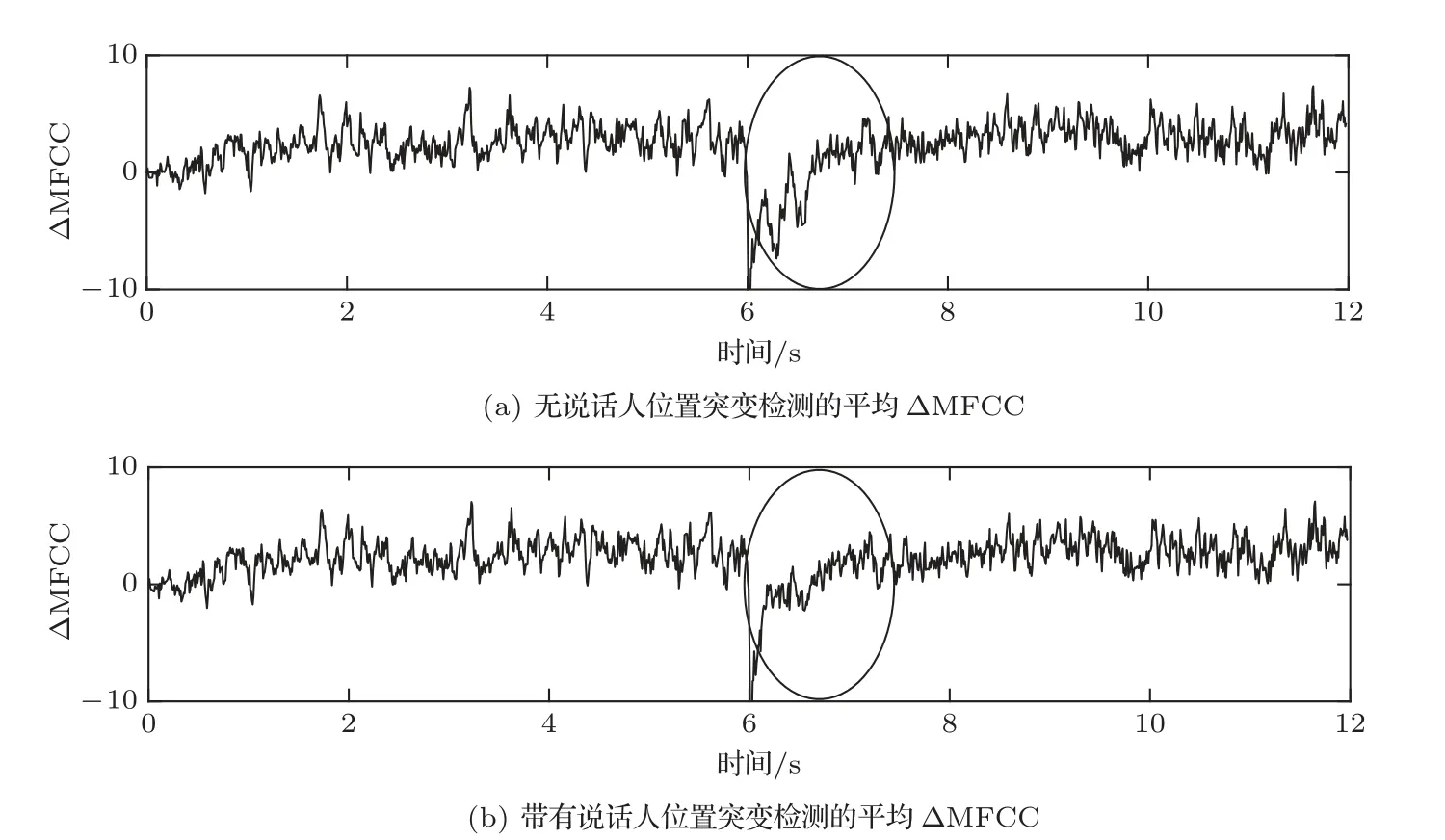
图4 MFCC距离改善Fig.4 MFCC distance improvement

图5显示了混响时间T60=500 ms下的语声信号语谱图，从图5(b)中可以看到，6 s时刻说话人位置的突变严重影响了去混响算法的效果，导致一段时间内的频谱结构变得比较模糊。而使用本文提出的带有说话人位置突变检测的去混响方法，相较于图5(b)，图5(c)中的语谱图在6～7 s这段时间内的模糊程度明显下降，模糊的频谱结构变得更加清晰。

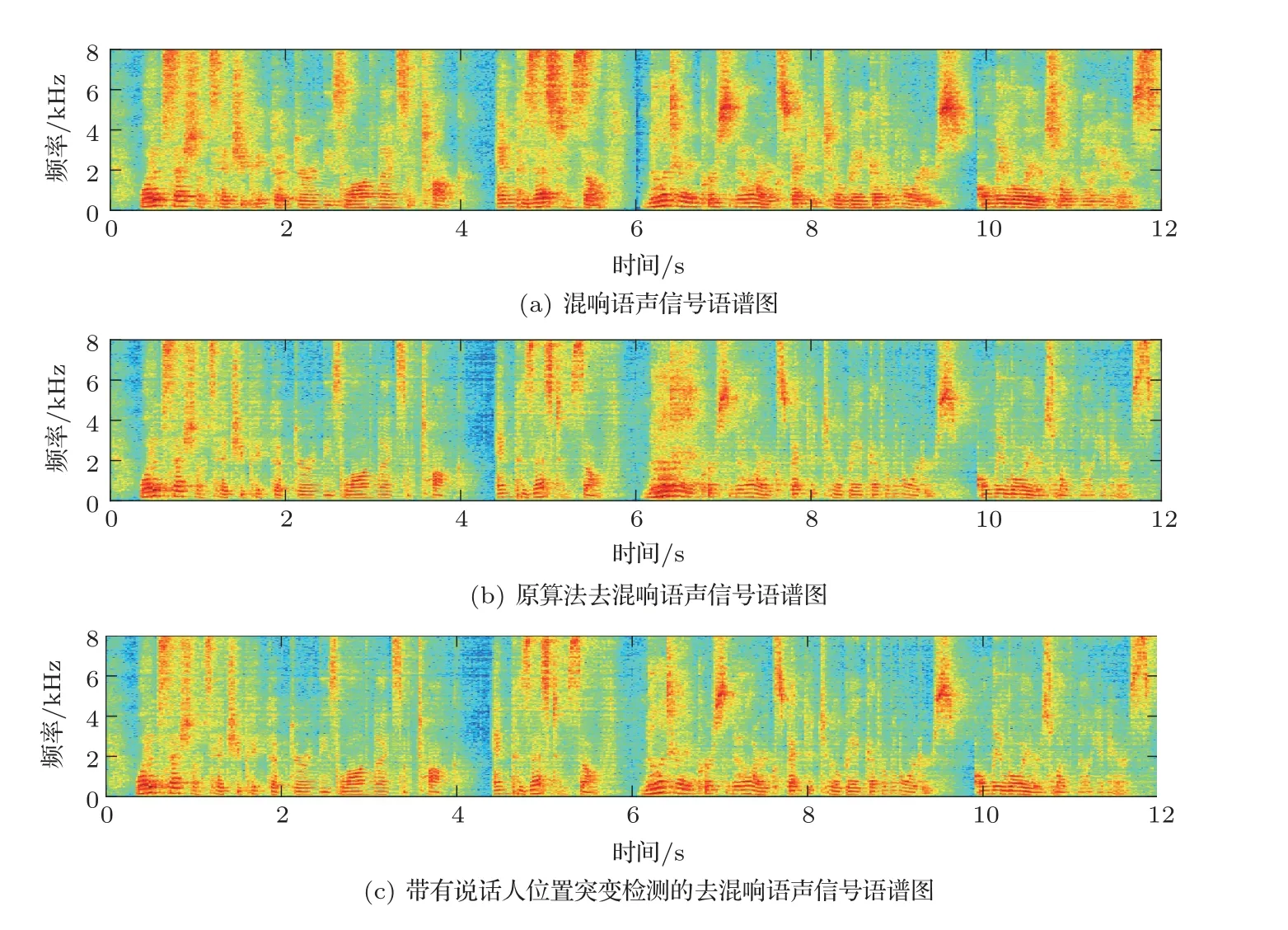
图5 语声信号语谱图Fig.5 Spectrogram of speech signal

3.2.3 高斯噪声环境下算法鲁棒性

该实验测试本文所提算法在加性高斯白噪声环境下的去混响性能。用PESQ得分和语声-混响调制能量比(Speech-to-reverberation modulation energy ratio,SRMR)[20]作为评价指标。

通过在混响信号中加入不同程度大小的高斯白噪声生成所需的测试信号，图6和图7分别显示了不同混响信噪比(Reverberation signal-to-noise ratio,RSNR)下，去混响信号的平均PESQ得分和平均SRMR。可以看出，本文所提出的带有声源位置突变的去混响算法在高斯白噪声环境下依然有很强的鲁棒性，在不同混响强度下的去混响效果相较于原算法都有较大提升。

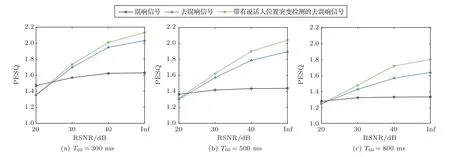
图6 不同噪声环境下的PESQ得分Fig.6 PESQ score in different noise environments

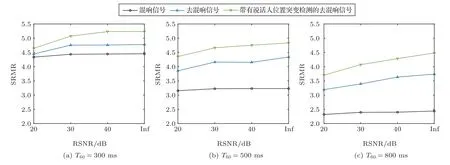
图7 不同噪声环境下的SRMR得分Fig.7 SRMR scores in different noise environments

3.3 实际环境录声仿真测试

为了更合理地评估所提算法的去混响性能，采集了真实房间记录的多组混响信号对算法进行验证，并测试了算法对不同声学比位置处(改变声源距传声器阵列的距离d)拾声信号的去混响性能。如图8所示，采用4个间隔为10 cm的传声器阵列，在一个混响时间约为700 ms的房间中采集混响信号，传声器阵列和扬声器的高度都为1 m，扬声器在6 s时从传声器阵列的左侧45°改变到右侧45°位置，每次实验播放的12 s纯净语声信号均取自TIMIT数据库。此外，为了增加实验的可验证性和丰富实验样本，提高实验结果的可靠性，本实验还采用了实际环境录声的多通道房间脉冲响应数据库[21]与TIMIT数据库的纯净语声信号进行卷积作为测试信号。最终的实验结果是真实房间记录的混响信号和MARDY数据库样本的平均值。

图8 传声器位置示意图Fig.8 Diagram of the microphone position

随着声源与传声器之间距离的增加，传声器所采集语声信号的混响强度也会增加，语声质量也随之下降。图9为声源距传声器阵列不同距离时的PESQ得分和SRMR，可以看出，对于说话人位置突变的语声信号，本文所提出的带有说话人位置突变检测的去混响算法均有效地提高了混响语声信号的质量。

图9 声源距传声器不同距离时算法平均PESQ和SRMR得分Fig.9 The algorithm averages PESQ and SRMR scores when the sound source is different from the microphone

4 结论

本文研究了一种能够检测说话人位置变化的自适应语声去混响方法，该方法采用RLS算法实现滤波器系数的自适应估计更新，如果声源的位置发生变化，该方法将检测这些变化并重新初始化滤波器系数的估计，使基于RLS的MCLP去混响方法对目标声源的位置变化更具鲁棒性。仿真实验的结果验证了该方法的有效性。