次级声源优化布放的局部空间有源降噪

冯雨薇王晓琳 崔笑颜杨 军

(1中国科学院噪声与振动重点实验室(声学研究所)北京100190)

(2中国科学院大学 北京100049)

0 引言

有源噪声控制(Active noise control,ANC)技术基于相消性干涉原理，通过产生与初级声波幅度相同、相位相反的次级声波，以达到降噪目的[1-3]。影响ANC系统降噪量的因素有很多种[4]，次级声源和误差传声器的数目和位置直接影响了静区的大小和系统的输出功率[5-6]。随着波长的减小，需要更多的次级声源来达到好的降噪效果[1]。实际工程应用中，例如汽车内的路噪有源控制系统、舱室内休息区的有源头枕系统，由于系统通道数、系统计算能力、硬件复杂度等因素的限制，进行次级声源优化布放是这些控制系统需要解决的问题。

在声场控制技术中，次级声源的优化布放可以看成组合优化问题，即从所有可能的组合中选择效果最好的组合方案[7]。因为问题的非凸性，常采用遗传算法[8-10]和模拟退火算法[11-12]来搜索最优组合。然而，遗传算法和模拟退火算法需要设定一些参数，包括种群规模、交叉概率、变异概率等，需要根据特定问题进行参数选择，此类算法容易陷入局部最优解，而不是全局最优解。当面临复杂模型的次级声源优化布放问题时，算法的参数选择更加困难且计算时间成倍增加，故不适用于实际复杂模型的次级声源优化布放应用。次级声源的优化布放是一个非凸优化的问题，可以通过改变代价函数，将非凸优化问题变为凸优化问题，主要方法有Lilis等[13]提出的最小绝对值压缩选择

(Least absolute shrinkage and selection operator,LASSO)算法、Khalilian等提出的约束匹配追踪(Constraint matching pursuit,CMP)[14]算法和奇异值分解(Singular value decomposition,SVD)[15]算法。Khalilian等[16]对比了这3种方法，当有能量约束时，利用l2范数约束的CMP算法进行扬声器的优化布放，重现效果更好；当无能量约束时，利用l1范数约束的LASSO算法的重现效果更好。Liu等[17]研究了结合优化次级声源阵列和约束点零声压约束的模态匹配-加权最小二乘(Weighted least squares-constraint matching pursuit,WLS-CMP)

算法，WLS-CMP算法可以提高误差区域的降噪量，且抑制非误差区域的声功率增加。陈克安等[7]研究了基于声场分解和LASSO算法的次级声源优化布放算法(Wave domain-sparsity inducing regularization,WD-SIR)，当激励次级声源数目较小时，遗传算法和WD-SIR方法的降噪效果相似，WD-SIR方法的系统稳定性优于遗传算法。

以上研究大多集中在自由声场中，利用点声源的理想传递函数进行次级声源优化布放仿真研究，尚未进行实验研究及系统比较不同范数约束的次级声源优化布放算法的真实降噪效果。为实现更好的降噪效果，本文提出一种根据真实次级通路传递函数进行次级声源优化布放的局部空间有源控制系统，并从降噪量、降噪均匀度和次级声源能量这3个方面详细比较了两种次级声源优化算法与次级声源均匀布放的实际降噪效果。本文应用的第一种次级声源优化算法是采用l2范数约束的CMP算法，第二种次级声源优化算法是采用l1范数约束的稀疏正则化方法。在全消声室中利用扬声器线阵进行多通道有源降噪实验研究，实验结果表明，在200～1000 Hz，次级声源优化布放的控制系统的平均降噪量比次级声源均匀布放的控制系统的平均降噪量多5 dB左右，在1100～1900 Hz，次级声源优化布放的控制系统的平均降噪量比次级声源均匀布放的控制系统的平均降噪量多11～13 dB。次级声源优化布放的控制系统的降噪量分布更加均匀且次级声源输出能量更小。两种优化算法中，采用稀疏正则化方法的降噪效果更佳。本文所提出的根据实测传递函数进行次级声源优化布放的方法可以为实际工程应用中(比如汽车内的路噪有源控制系统、舱室内休息区的有源头枕系统)的次级声源优化布放提供参考。

1 次级声源均匀布放的有源控制系统滤波器系数设计

本文中使用多通道前馈、固定系数有源控制系统，通过离线辨识方法对次级通路进行建模，结合初级噪声源的信息，计算滤波器系数的维纳解，利用次级信号来抑制误差传声器处的初级噪声，从而达到降噪的目的。对于初级噪声平稳的系统，该方法的控制效果最优[4,18]。

次级声源均匀布放的多通道有源控制系统的示意图如图1所示。设该系统有P个初级噪声源，Q个次级声源，M个误差传声器，hmq为第q个次级声源到第m个误差传声器的次级通路传递函数的脉冲响应[4]，hmp为第p个初级噪声源到第m个误差传声器的初级通路传递函数的脉冲响应，dm(n)为初级噪声源在第m个误差传声器处的期望信号，x(n)为参考信号。根据叠加原理，误差信号为期望信号与次级信号之和。第m个误差传声器处的误差信号为[4,18]

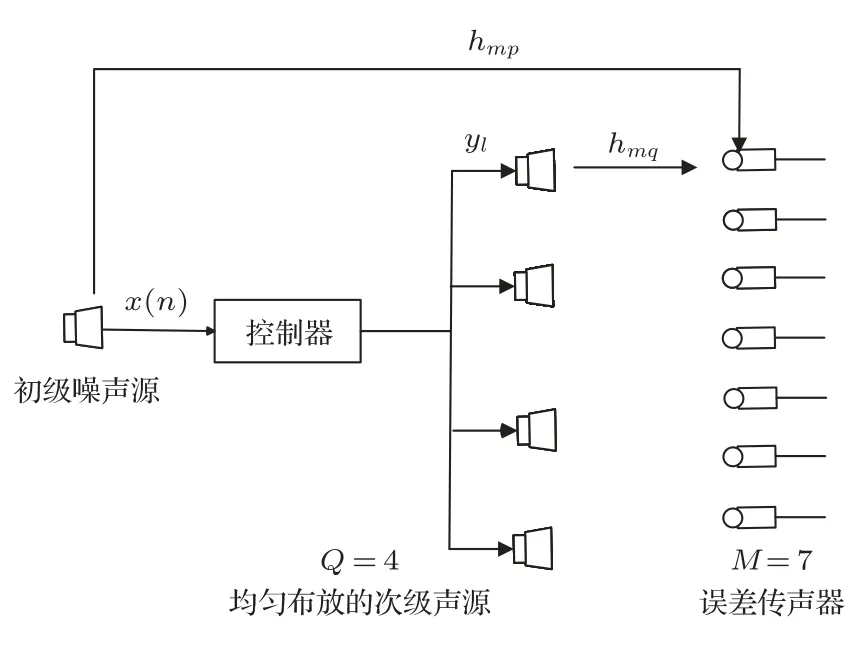
图1 次级声源均匀布放的有源控制系统简化框图Fig.1 Block diagram of the ANC system with the uniformly placed secondary sources

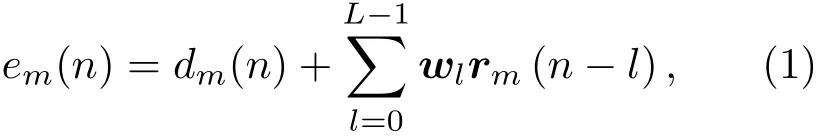
其中，各次级声源的第l阶滤波器系数组成的向量wl=[w1l,w2l,···,wQl]，L为滤波器长度，滤波-x信号组成的向量为rm(n)=[rm1(n),rm2(n),···,rmQ(n)]。控制系统的目标函数[4,19]为

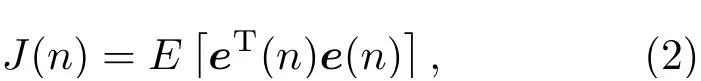
其中，误差信号向量为e(n)=[e1(n),e2(n),···,em(n)]T，E(·)表示对自变量取时间平均。记滤波器系数矩阵为令，最佳滤波器系数矩阵Wopt为

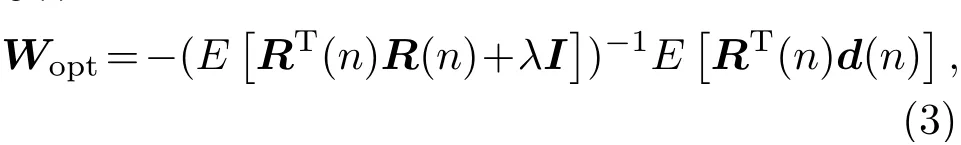
其中，I为单位矩阵，λ为正则化参数。期望信号向量为d(n)=[d1(n),d2(n),...,dm(n)]T。自相关矩阵R(n)为

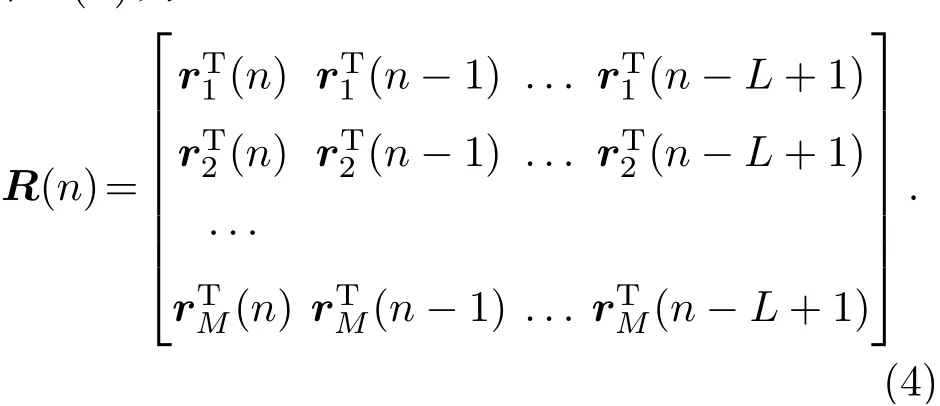
2 次级声源优化布放的有源控制系统滤波器系数设计

本节介绍次级声源优化布放的有源控制系统的滤波器系数设计。本文分别应用两种范数约束的次级声源优化布放算法对有源控制系统中的次级声源进行优化布放，再利用维纳解来计算各个选中次级声源的滤波器系数。这两种次级声源优化布放算法分别是l2范数约束的CMP算法和l1范数约束的利用凸优化工具箱求解的稀疏正则化方法(CVXL1)。2.1节介绍了基于CMP算法的有源控制系统的滤波器系数设计，2.2节介绍了基于CVXL1方法的有源控制系统的滤波器系数设计。

2.1 基于CMP算法的有源控制系统滤波器系数设计

基于次级声源优化布放的多通道有源控制系统的示意图如图2所示，其中黑点代表备选次级声源。设该系统有P个初级噪声源，K个备选次级声源，M个误差传声器，选中次级声源数目为Q。通过次级声源优化布放算法，将从K个备选次级声源中选出Q个优化布放的次级声源。hmk为第k个备选次级声源到第m个误差传声器的次级通路传递函数的脉冲响应。第k个备选次级声源到第m个误差传声器的次级通路传递函数的脉冲响应向量为hmk=[hmk0,hmk1,···,hmk(B-1)]，B为次级通路阶数。备选次级声源到误差传声器的次级通路函数的脉冲响应矩阵hMK(矩阵维度M×K)可写为

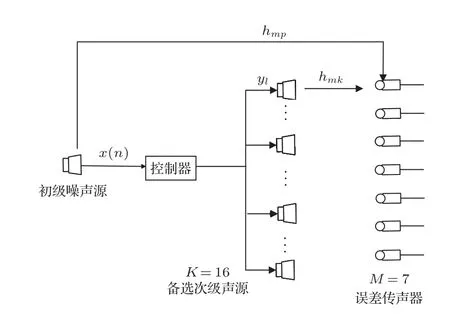
图2 次级声源优化布放的有源控制系统简化框图Fig.2 Block diagram of the ANC system with the optimized secondary source placement

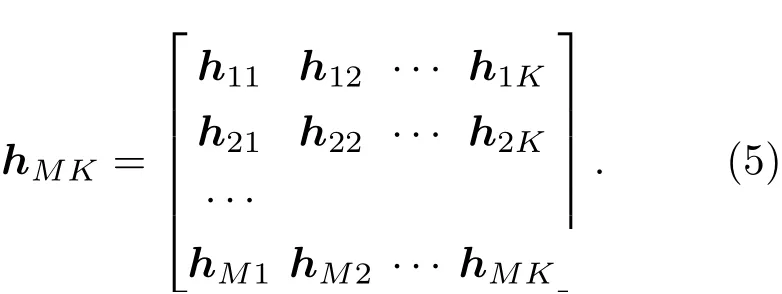
对次级通路传递函数的脉冲响应向量hmk进行傅里叶变换，在f频点，备选次级声源到误差传声器的频域传递函数矩阵HMK(矩阵维度M×K)可写为

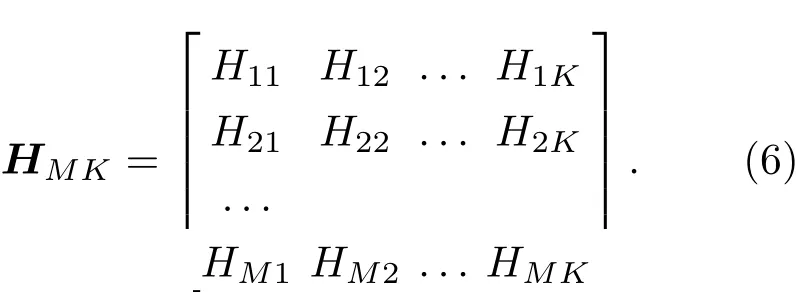
同理，对初级通路传递函数的脉冲响应向量hmp进行傅里叶变换，在f频点，初级噪声源到误差传声器的频域传递函数矩阵HMP(矩阵维度M×P)可写为

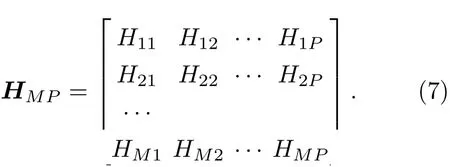
CMP算法对次级声源的强度进行l2范数约束，即在对次级声源的能量进行约束的情况下，使得误差区域的总声压能量最小。在有源降噪问题中，它的代价函数为[14]

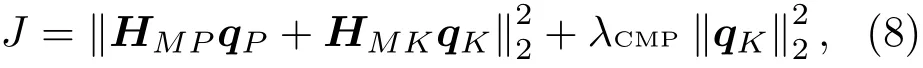
其中，qP为初级噪声源的强度向量，qK为次级声源的强度向量，HMP为初级噪声源到误差传声器的频域传递函数矩阵，HMK为备选次级声源到误差传声器的频域传递函数矩阵，λCMP为正则化参数。

本文中，CMP算法优化选取次级声源和求解次级声源滤波器系数过程如下：备选次级声源依次发出白噪声信号，进行次级通路辨识，利用式(5)、式(6)计算备选次级声源到误差传声器的频域传递函数矩阵HMK。初级声源发出连续单频信号，误差传声器采集期望信号，利用式(7)计算初级声源到误差传声器的频域传递函数矩阵HMP。将备选次级声源到误差传声器的频域传递函数矩阵HMK、初级噪声源到误差传声器的频域传递函数矩阵HMP输入到CMP算法[14]中，经过Q次循环，每次循环中，遍历所有备选次级声源，找到与当前残差声场最匹配的一个次级声源，并计算该次级声源的强度，更新残余误差声场。Q次循环后，即可找到Q个优化的次级声源。将正则化参数设为λ=10-4，利用式(3)计算选出的Q个次级声源的滤波器系数。

2.2 基于稀疏正则化方法的有源控制系统滤波器系数设计

CVXL1方法对次级声源的强度进行l1范数约束，即在对次级声源的数目进行约束的情况下，使得误差区域的总声压能量最小。在有源降噪问题中，它的代价函数为

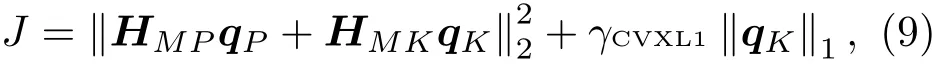
其中，γCVXL1表示稀疏度调节参数，用于约束次级声源的数量。一般来说，γCVXL1取值越大，发声次级声源数量越少。式(11)也是LASSO算法的代价函数[13]。

本文中，CVXL1方法优化次级声源的选取和次级声源滤波器系数求解过程如下：将实测的备选次级声源到误差传声器的频域传递函数矩阵HMK、初级噪声源到误差传声器的频域传递函数矩阵HMP输入到CVXL1算法的代价函数中，利用凸优化工具箱对式(9)求解，得到次级声源强度解qK，对qK中的元素的幅值进行排序，选取对应幅值最大的Q个次级声源为CVXL1方法所选出的优化次级声源。利用式(3)计算选出的Q个次级声源的滤波器系数。

3 实验与控制效果分析

3.1 评价指标

为了量化评价次级声源均匀布放的控制系统和次级声源优化布放的控制系统的降噪效果，本文将从3个指标进行评价。这3个指标分别是误差区域的降噪量、误差区域的降噪均匀度和次级声源能量。

第一个指标是误差区域的降噪量，定义误差区域的降噪量为NR，

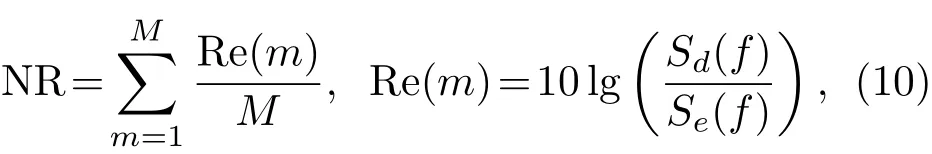
其中，M为误差传声器的数目，Re(m)为第m个误差传声器的降噪量，Sd(f)为降噪之前的信号的功率谱，Se(f)为降噪之后的信号的功率谱。

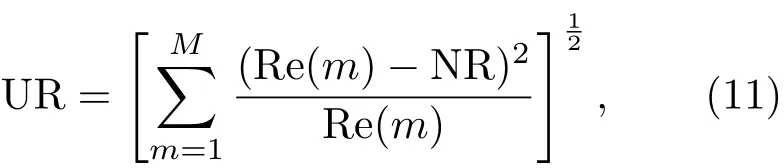
第二个指标是降噪量均匀度，定义误差区域的降噪均匀度为UR，其中，UR代表所有误差传声器降噪量的标准差，UR越小，说明降噪量在误差区域分布的越均匀。

第三个指标是次级声源的能量，定义系统的次级声源能量为Power,

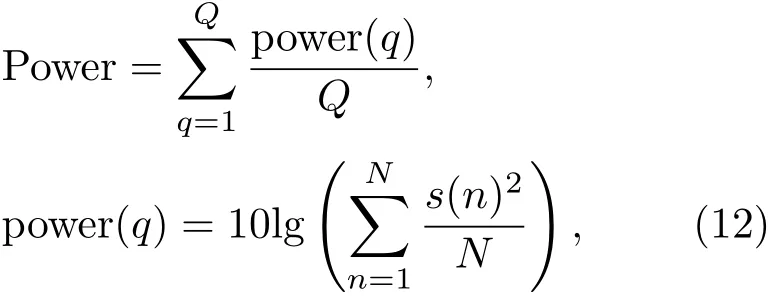
其中，Q为次级声源的数目，power(q)为第q个次级声源的输出能量。s(n)为次级声源输出信号，N为信号的采样点数。系统的次级声源能量过大，会引起非误差区域的声能量增加，且长时间工作，会损坏器件[7]。

3.2 实验结果与分析

实验在全消声室中进行，比较了次级声源均匀布放的ANC系统控制效果和次级声源优化布放的ANC系统控制效果。实验系统结构如图3所示，实际布置如图4所示。控制系统的实现基于TMS320C6678 DSP芯片开发板，系统的采样率为8 kHz。实验布置了1个初级噪声源、16个备选次级声源和7个误差传声器。分别通过CMP算法和CVXL1方法从16个备选次级声源中选出4个优化的次级声源。备选次级声源的间距是20 cm，该阵列距离铁丝网87 cm；误差传声器的间距是10 cm，该阵列距离铁丝网114 cm；初级噪声源距离备选次级声源线阵中心的距离为194 cm，距离铁丝网114 cm；传声器线阵中心到次级声源线阵中心的距离为104 cm。初级噪声源发射的初级噪声是200～1900 Hz的连续单频信号，频率间隔为100 Hz。

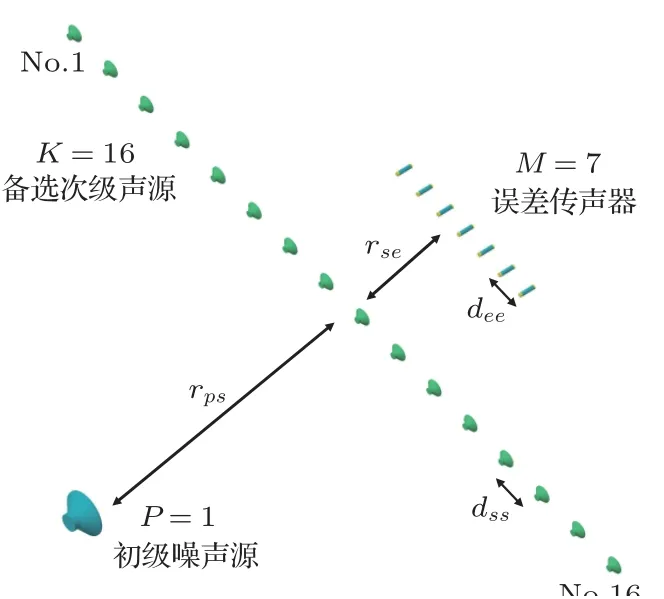
图3 次级声源优化布放的多通道前馈有源控制系统实验结构示意图Fig.3 Experimental geometric configuration of the multi-channel feedforward ANC system with the optimized secondary source placement

图4 次级声源优化布放的有源降噪实验布置图Fig.4 Actual layout of the active noise control experiment with the optimized secondary source placement

在每个频点，实验测试步骤如下：

第一步，备选次级声源依次发出白噪声，进行次级通路建模，次级通路阶数B=512。将次级通路的脉冲响应进行傅里叶变换，得到某频点的备选次级声源到误差传声器的传递函数矩阵HMK(矩阵维度7×16)。

第二步，初级噪声源发出连续单频信号，误差传声器采集期望信号。同时，理想参考信号直接从初级噪声源信号获取至控制器芯片开发板。对期望信号进行傅里叶变换，得到该频点的初级噪声源到误差传声器的传递函数矩阵HMP(矩阵维度7×1)。

第三步，利用两种次级声源优化布放算法进行次级声源的优化布放。将第一步和第二步中实测的备选次级声源到误差传声器的传递函数矩阵HMK和初级噪声源到误差传声器的传递函数矩阵HMP分别输入到CMP算法、CVXL1算法中，经过计算，可以得到不同算法选出的优化布放的4个次级声源。次级声源均匀布放的系统，无需经过次级声源优化选点过程，其固定的次级声源为1号、6号、11号、16号次级声源。

第四步，计算各次级声源的滤波器系数及理论降噪量。利用式(3)计算选中的4个次级声源的维纳滤波器系数，滤波器长度L=512，其余12个次级声源滤波器系数置零。为公正比较优化算法的选点结果，将正则化参数和稀疏度调节参数统一设为λ=10-4，利用式(10)计算理论仿真降噪量。

第五步，进行控制并计算实际降噪效果的评价指标。误差传声器采集控制开启前和开启后的信号。利用式(10)、式(11)、式(12)分别计算各个方法的误差区域实验降噪量、降噪均匀度以及次级声源能量。

3.2.1次级声源选点位置比较

不同频率工况下，CVXL1方法和CMP算法的次级声源选点结果如图5所示，图中蓝色三角表示CVXL1方法选中的次级声源位置，红色圆点表示CMP算法选中的次级声源位置。作为对比，图5(a)、图5(d)、图5(g)、图5(j)列出了不同频率下次级声源均匀布放的最小二乘(Least-squares algorithm with the uniformly placed secondary sources,LSUni)算法的次级声源位置(紫色圆点)。从图5(a)～图5(l)的对比可看出，与均匀布放的次级声源相比，CVXL1方法和CMP算法的选出的次级声源距离初级噪声源更近，次级声源的位置更加集中。如图5(b)、图5(e)、图5(h)、图5(k)所示，CVXL1方法选出的次级声源位置随着频率的增加而变化，这是因为频率增加，波长变短，初级声场发生变化，为了达到好的控制效果，需要调整次级声源的间距，来更好地抵消初级声场。如图5(c)、图5(f)、图5(i)、图5(l)所示，与CVXL1方法相比，CMP算法选出的次级声源位置更加集中。

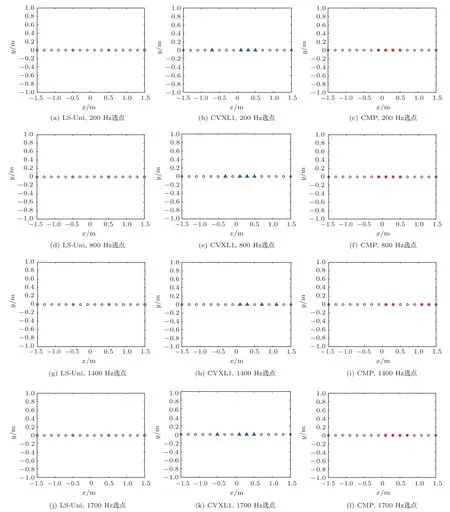
图5 不同方法次级声源选点示意图Fig.5 Secondary loudspeaker placement for different method

3.2.2 实验降噪量与理论降噪量比较

在200～1900 Hz，CVXL1方法、CMP算法和LS-Uni算法的理论降噪量和实际实验降噪量如图6所示，次级通路模型的估计误差、电噪声等不确定因素导致实际降噪量和理论降噪量存在差距。从降噪趋势看，CVXL1方法、CMP算法和LS-Uni算法都会随着初级声场频率的增高，降噪量减少，CVXL1方法和CMP算法的降噪量减小趋势更加缓慢。在600～1900 Hz，与LS-Uni算法相比，CVXL1方法和CMP算法的降噪量更多，且随着频率的增加，优势更加明显。在800～1900 Hz，CVXL1方法和CMP算法的降噪量比LS-Uni算法的降噪量多10～13 dB。这是因为随着频率的增大，LS-Uni算法的次级声源阵列间固定，逐渐不满足空间采样定理，所以降噪效果越来越差。CVXL1方法和CMP算法，随着频率的增加，会调整次级声源的间距，来更好地抵消初级声场，所以在高频仍有较好的降噪效果。在200～500 Hz，CVXL1方法的降噪量和LS-Uni算法的降噪量类似，CMP算法的降噪量比其他方法的降噪量少1～2 dB。这是由于CMP算法在200～500 Hz的选点比较集中，次级声源的间距太小，而低频的初级声场的波长较长，次级声源间距小的次级声场无法较好抵消初级声场。

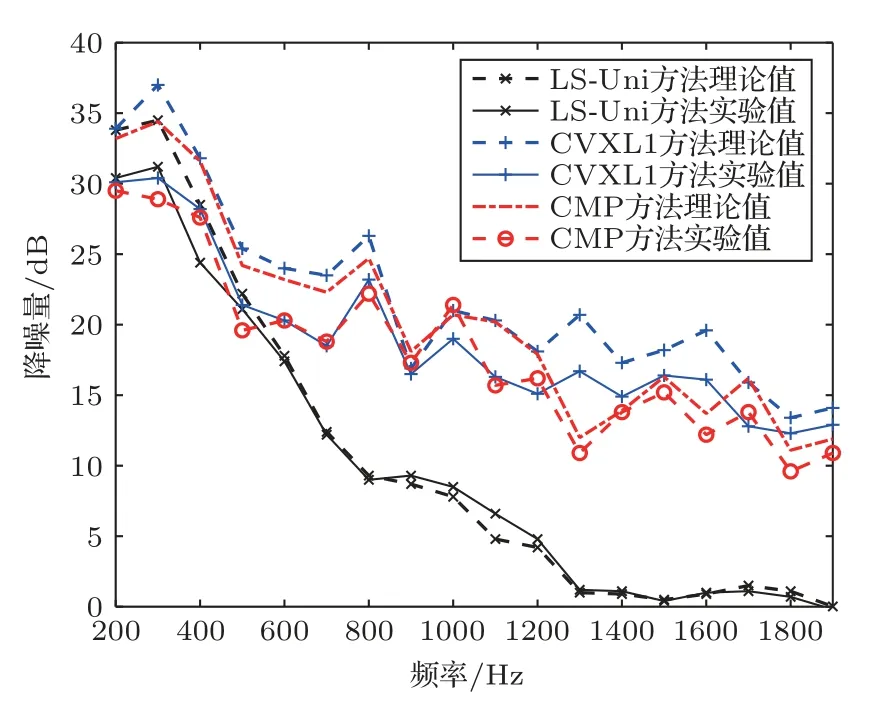
图6 在200～1900 Hz，各个方法的降噪量实验值、理论值比较Fig.6 Comparison of the experimental and theoretical noise reductions for each method from 200 Hz to 1900 Hz

3.2.3 次级声源能量比较

在200～1900 Hz，CVXL1方法、CMP算法和LS-Uni算法的次级声源能量如图7所示。在大多数频点，CVXL1方法、CMP算法的次级声源能量比LS-Uni算法的小，这是因为优化方法选出的次级声源分布在更重要的位置上，使用较少的能量就可以达到较好的降噪效果。在900 Hz，CMP算法的次级声源能量较大，是因为选中的8号、9号、10号、11号次级声源，间距为20 cm，900 Hz初级声场的半波长为19 cm，选中次级声源位于900 Hz的半波长位置附近，需要更多的次级声源能量，才能达到较好的降噪效果。

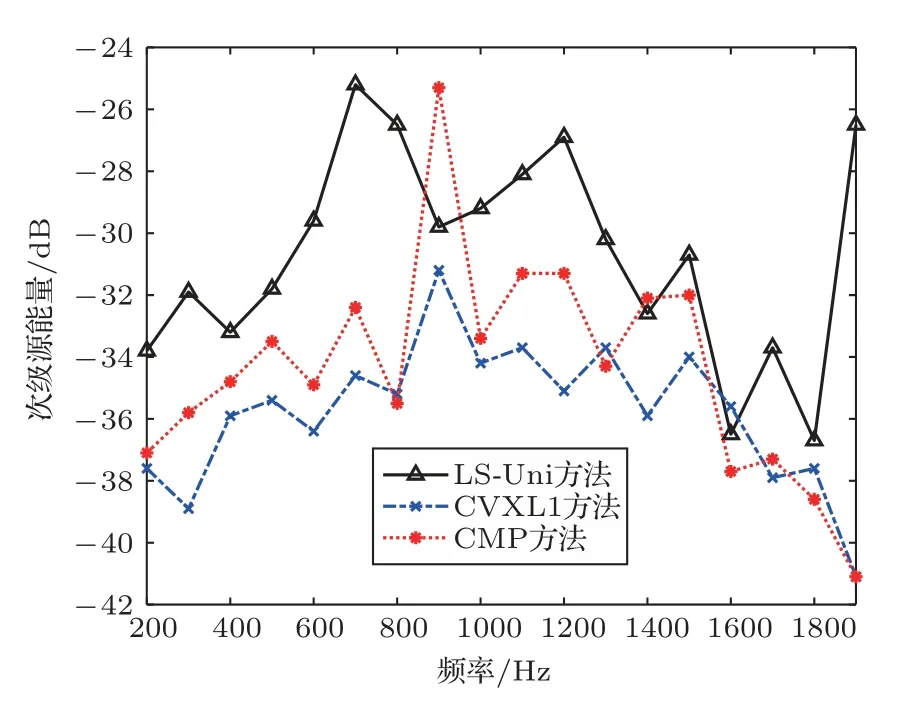
图7 在200～1900 Hz，各个方法的次级声源能量比较Fig.7 Comparison of the secondary source power for each method from 200 Hz to 1900 Hz

3.2.4实际降噪均匀度比较

在200～1900 Hz，CVXL1方法、CMP算法和LS-Uni算法18个频点的降噪均匀度的箱线图如图8所示。每个方法的箱线图中，上下黑色实线分别表示均匀度的最大值和最小值，上下蓝色实线分别表示均匀度的上四分位数和下四分位数，红色实线表示均匀度的中位数。可以看出，CVXL1方法、CMP算法的降噪均匀度整体(最大值、最小值、上下四分位数、中位数)都比LS-Uni算法的降噪均匀度小，说明运用次级声源优化布放算法的控制系统的降噪量在误差区域分布得更加均匀。

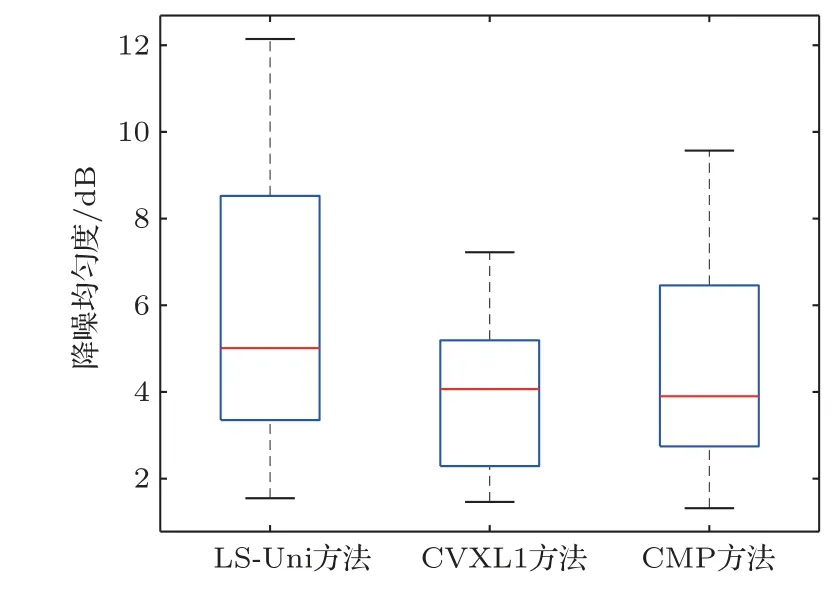
图8 各个方法的降噪均匀度比较Fig.8 Comparison of the uniformity of noise reduction for each method

3.2.5 平均降噪效果比较

各个方法在不同频率范围的平均降噪量、平均降噪均匀度和平均次级声源能量如表1所示。在200～1000 Hz，两种次级声源优化布放算法的平均降噪量约为23 dB，比LS-Uni算法多5 dB；在1100～1900 Hz，两种次级声源优化布放算法的平均降噪量比LS-Uni算法多11～13 dB，使用l1范数约束的CVXL1方法的平均降噪量比使用l2范数约束的CMP算法的平均降噪量多1.7 dB。两种次级声源优化布放算法的平均降噪均匀度比LS-Uni算法的平均降噪均匀度小1～2 dB，其中，CVXL1方法的降噪量分布更加均匀。两种次级声源优化布放算法的平均次级声源能量比LS-Uni算法的平均次级声源能量少3～5 dB；运用CVXL1方法的控制系统的次级声源能量更小，为-35.8 dB。综合来看，次级声源优化布放的控制系统比次级声源均匀布放的控制系统有更多的降噪量，降噪量在误差区域分布更均匀且次级声源输出能量更小。其中，基于CVXL1方法的控制系统的降噪效果更佳。

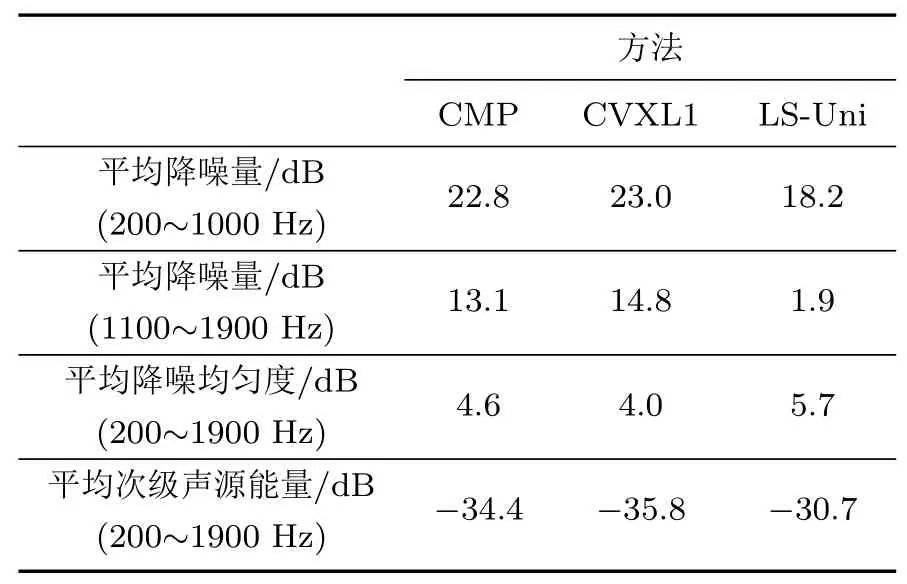
表1 各个方法的平均降噪效果Table 1 Average control performance for each method

值得说明的是，在本次全消声室的实验场景中，使用l1范数约束的CVXL1方法的降噪效果更好，在其他应用场景中，可以按照本文提出的实验测试步骤，分别用CMP方法和CVXL1方法选取次级声源并计算理论降噪量，选取理论降噪量更多的次级声源组合。不同的应用场景中，每种次级声源优化布放方法的降噪效果表现不同。值得注意的是，本文中的CMP方法和CVXL1方法是基于单频声场的次级声源优化布放方法，当面对宽带声场的次级声源优化布放问题，可以分析其频率成分，根据其频域能量分布来选取合适的次级声源组合。

4 结论

实际应用中，ANC系统的次级声源数目和系统能量是有限的。为实现更优的降噪效果，根据实际次级通路传递函数，本文提出了一种次级声源优化布放的局部空间有源控制系统并详细比较了两种范数约束的次级声源优化方法与次级声源均匀布放的实际降噪效果。应用的第一种次级声源优化算法是采用l2范数约束的CMP算法，第二种次级声源优化算法是采用l1范数约束的CVXL1方法。在全消声室中利用扬声器线阵进行多通道有源降噪实验研究，实验结果表明，次级声源优化布放的控制系统比次级声源均匀布放的控制系统有更多的降噪量，降噪量在误差区域分布更均匀且次级声源输出能量更小。在200～1000 Hz，次级声源优化布放的控制系统的平均降噪量比次级声源均匀布放系统的平均降噪量多5 dB左右，在1100～1900 Hz，次级声源优化布放系统的平均降噪量比次级声源均匀布放系统的平均降噪量多11～13 dB。此外，两种优化算法中，采用CVXL1方法的降噪效果更佳。本文所提的根据实测传递函数进行次级声源优化布放的方法可以为实际工程应用中的次级声源优化布放提供参考。可以利用本文提出的测试步骤对实际工程应用场景的备选次级通路传递函数进行测量，再利用次级声源优化布放算法选出更为重要的次级声源位置，从而提高实际降噪效果。在未来的工作中，将会研究次级声源优化布放算法在更多实际场景中的应用。