基于改进果蝇算法优化BP神经网络的接地网腐蚀速率预测模型
程宏伟,高莲,于虹,李鹏
(1.云南大学 信息学院,昆明 650500; 2.云南电网有限责任公司电力科学研究院,昆明 650500)
0 引 言
随着现代电力技术的发展大容量、特高压输电线路相继出现,对保障电力系统安全稳定运行的接地网要求不断提高[1]。但接地网长期处于地下,复杂的土壤环境使其发生腐蚀甚至断裂,进而影响电力系统的安全稳定运行[2-4]。因此,研究预测结果准确的接地网腐蚀速率预测模型可以使运维人员及时掌握接地网健康状况,提前发现接地网的安全隐患并安排检修,避免因接地网的腐蚀造成电网故障,对整个电网的安全稳定运行至关重要[5-6]。
当前,主要通过传感器检测和建立腐蚀参数样本库两种方式对接地网腐蚀速率进行预测。针对第一种方法,文献[7]使用电化学腐蚀传感器对接地网进行观测并使用灰色预测的方法对观测参数进行分析得到接地网腐蚀速率,但这种方法只能短期预测接地网腐蚀且传感器成本较高,无法大范围的推广使用。针对第二种方法,文献[8]将现场采集的土壤参数作为BP神经网络的输入参数,建立接地网预测模型且具有较高的预测精度,但BP神经网络随机初始化权值和阈值存在收敛速度慢和稳定性差的不足;文献[9]通过相似度计算得到较优的训练样本并使用支持向量机(Support Vector Machine, SVM)对接地网腐蚀速率进行预测,但SVM存在着运算费时且核函数参数选择对实验结果产生较大影响的不足[10-11];文献[12]采用模糊理论对接地网腐蚀速率进行预测,但存在定义分函数不全面的问题,且由两位专家确定的可拓区间判断矩阵具有一定的随机性;文献[13-14]分别采用遗传算法-改进支持向量机-误差校正组合模型和人工蜂群算法(Artificial Bee Colony, ABC)优化SVM的ABC-SVM模型进行预测,但优化算法的初始种群随机产生,易导致种群分布不均匀,具有较强的随机性和盲目性。
鉴于此,为了进一步提高预测精度和预测稳定性,文中提出了基于改进果蝇算法(Update Fruit fly Optimization Algorithm, UFOA)优化BP神经网络的接地网腐蚀速率预测模型(UFOA-BP)。该模型首先利用混沌映射、动态半径搜索策略和优化气味浓度判定公式对果蝇优化算法(Fruit fly Optimization Algorithm, FOA)的种群位置、搜索步长和气味浓度判定公式进行改进,然后将UFOA算法与BP神经网络相结合优化BP神经网络的初始连接权值和阈值,最后以文献[14]对某地24座变电站的测量计算数据进行验证。结果表明,相较于其他预测方法,UFOA-BP模型在腐蚀速率预测时具有更高的预测精度和模型稳定性,对运维人员提前发现接地网安全隐患并安排检修进而保障电网安全稳定运行具有重要意义。
1 基于UFOA优化BP神经网络的接地网腐蚀速率预测模型
1.1 BP神经网络原理
由于BP 神经网络优秀的非线性映射能力,在进行数据预测时无需建立精准的数学模型,且具有较高的预测精度,因此在数据预测方面有着较为广泛的应用[15-18]。
标准 BP 神经网络主要分为两方面:一方面是向前的信息传递,即对于输入的信息按照输入层、隐含层和输出层进行正向传递;另一方面是反向的信号传播,即根据实际值与预测值的误差进行反向传播修改各层连接的权值[19-20]。其具体实现如图1所示。
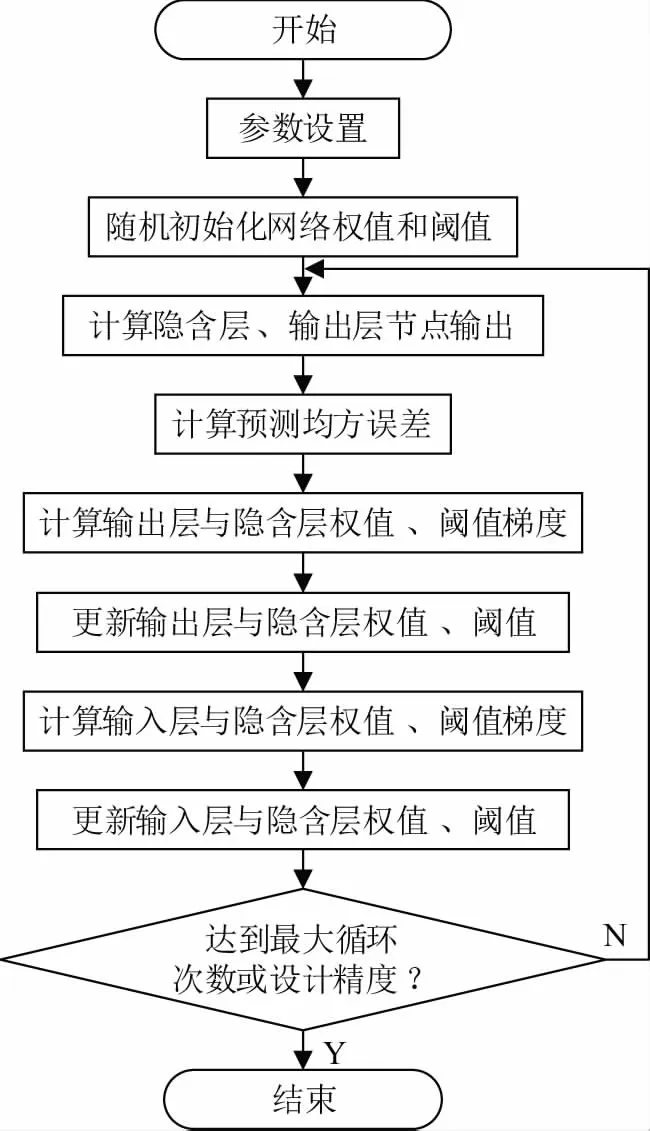
图1 BP神经网络流程图
从图1可以看出,BP神经网络的初始权值和阈值是随机产生的且利用梯度下降的方法进行修正,这样工作机制使BP神经网络对初始权值异常敏感,增加了算法的求解难度和收敛时间。针对BP神经网络存在的不足,文中使用UFOA算法优化BP网络的初始权值和阈值,进一步提高BP神经网络预测的稳定性和准确性。
1.2 FOA算法原理
FOA算法是Pan[21]受果蝇觅食行为启发于2012年提出的一种群体智能全局优化算法。FOA算法通过模拟果蝇群体觅食行为,采用群体协作、信息共享的机制进行寻优操作[22],文献[23-24]从计算精度、计算量和计算复杂度三个方面对免疫算法、遗传算法、蚁群算法、粒子群算法、鱼群算法和FOA算法进行了详细比较,得到FOA算法具有较高寻优精度,且算法简单、计算量较小的结论,因此文中以FOA算法作为优化算法展开研究。
FOA算法由两部分构成:首先,利用果蝇种群的嗅觉进行搜索,得到果蝇种群中离目标最近的个体;然后,通过果蝇视觉进行寻找,确定最佳果蝇个体的位置坐标,同时其它果蝇向最佳位置方向飞去。以此反复,直至达到最大迭代次数或目标精度为止,其步骤如下:
(1)参数设置:
设置FOA算法的最大迭代次数、目标精度、种群数量和搜索半径:
(2)随机初始化果蝇种群位置:

(1)
(3)果蝇个体利用嗅觉搜寻食物:
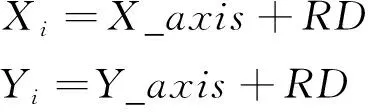
(2)
(4)计算果蝇与原点之间的距离:
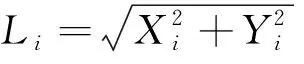
(3)
(5)计算果蝇味道浓度判定值:
Si=1/Li
(4)
(6)计算果蝇味道浓度:
Smelli=f(Si)
(5)
(7)寻找味道浓度最佳的果蝇个体:
[bestSmell,bestIndex]=min(Smell)
(6)
(8)果蝇利用视觉向最佳果蝇个体飞去:

(7)
(9)判断是否达到最大循环次数或目标精度,若未达到,循环步骤(3)~步骤(8),若达到,返回最优果蝇个体。
从步骤(2)可以看出FOA算法使用随机初始化果蝇群体位置的方法,该方法存在种群分布不均匀和算法具有一定盲目性的问题;从步骤(4)可以看出果蝇觅食阶段采用固定的搜索半径进行寻找,一方面会增加收敛时间,另一方面降低了收敛精度,甚至使算法陷入局部最优;从步骤(6)可以看出果蝇的气味浓度判定值恒为正值,无法实现负值区域的搜索,造成算法全局搜索能力下降。
因此,对FOA算法存在的盲目初始化果蝇种群位置,收敛速度和收敛精度有待进一步提高以及无法实现负值区域搜索的问题进行改进。
1.3 UFOA算法
由于FOA算法存在随机确定初始果蝇种群位置的特点,使得算法具有一定的随机性和盲目性,且固定的果蝇搜索半径使收敛速度和收敛精度有待进一步提高以及无法实现负值区域搜索的缺陷。为提高果蝇种群的多样性和搜索的遍历性,增强算法的收敛精度,扩大算法的搜索范围,文中将从以下三个方面进行改进:
(1)引入Logistic混沌映射生成果蝇群体的初始位置,解决随机初始化种群分布不均匀问题,提高搜索群体的多样性和均匀性,增强算法的稳定性;
(2)引入动态搜索半径策略实现算法的搜索半径自适应动态调节,提高算法的收敛精度减小算法的收敛时间;
(3)改进FOA算法气味浓度判定公式,避免气味浓度判定值恒为正对算法的影响,扩大算法的搜索范围,增强算法的适应性。
1.3.1 Logistic映射
针对随机初始化果蝇种群易造成分布不均匀的问题,文中采用最简单有效的混沌映射解决方案[25]-Logistic 混沌映射,对所有果蝇位置初始化,从而使得优化后的果蝇位置具有混沌现象随机性、遍历性和规律性的特点[26-27],其系统方程如下:
x(n+1)=μx(n)(1-x(n))x(n)∈[0,1]
(8)
式中n为迭代次数;μ为控制参数,当μ=4时,系统处于混沌状态。
混沌变量Cxi的变换式如下:
Cx(n+1)i=4Cx(n)i(1-Cx(n)i),i=1, 2,…,N
(9)
式中Cx(n)i为第i个混沌变量在第n步混沌变换后的大小,通过式(9)得到第n+1次变换后的混沌变量Cx(n+1)i,然后结合式(10)和式(11)与变量Cxi∈[0,1]反复进行混沌映射[28]。

(10)
(11)
式中xi为混沌映射前的第i个原始数据,且xi∈[amin,amax];x′i为其映射后的值。
1.3.2 动态搜索半径策略
FOA算法在果蝇觅食阶段采用固定的搜索半径进行寻找,会降低算法的收敛精度,延长收敛时间,甚至陷入局部最优。因此,文中设计一种全新的动态搜索半径生成方法如式(12)所示,解决固定半径存在的不足,令算法在早期具有较大的搜索半径,增强算法全局的搜索能力,避免局部最优,搜索半径随着迭代次数的增加而减小,提高算法整体的收敛精度,减少收敛时间。
(12)
式中rmax和rmin分别表示最大和最小的搜索半径,iter表示当前迭代次数,Miter表示最大迭代次数。当搜索半径区间为[0.1,5],最大迭代次数为300时,搜索半径r的变化曲线如图2所示。

图2 搜索半径变化
如图2所示,改进后的搜索半径生成方法可以实现搜索半径随迭代增加的动态生成,解决了原有算法固定搜索半径的不足。
1.3.3 优化气味浓度判定值
从1.2节中的Step5可以看出,FOA算法的味道浓度判定值为果蝇个体与坐标原点之间距离的倒数,其值范围恒为正,无法实现负面空间解决方案搜索,缺乏对高纬度和复杂化问题的求解能力。因此文中优化了气味浓度判定公式,如式(13)所示:
Si=exp-Li×sgn(Xi×Yi)
(13)
式(13)中指数函数确保了候选解与果蝇位置的负相关,同时使用sgn函数,当果蝇个体在二维坐标的二、四象限时,Si为负值。通过式(13)可以实现对负值空间的全面搜索,增加了算法的应用场景,提高了算法对高纬度和复杂化问题的求解能力。
综上所述,针对 FOA 算法种群随机初始化、收敛速度和收敛精度有待进一步提高以及气味浓度判定值恒为正的问题,文中依次采用Logistic混沌映射、动态搜索半径策略和优化气味浓度判定值的方法实现对 FOA 算法进行改进。
1.4 UFOA-BP算法实现
UFOA优化BP网络的核心思想是在BP网络局部寻优能力基础上,利用UFOA 的全局寻优能力对BP网络的泛化能力和学习性能进行优化,根据UFOA迭代寻优过程中果蝇位置的改变对应于BP网络学习过程中权值与阈值的更新过程,寻找最合适的初始连接权值和阈值,提高BP网络的预测能力和预测效率。
其基本方法为:首先将果蝇个体视作BP神经网络的权值和阈值,用实际值和预测值的误差绝对值之和作为UFOA算法的适应度函数;然后通过UFOA 迭代寻优代替BP网络中的梯度修正;最后将最优果蝇个体作为BP网络的初始权值和阈值。其基本流程如图3所示。

图3 UFOA-BP算法流程图
2 预测结果对比及分析
2.1 数据预处理
文中使用的实验数据由文献[14]对某地24座变电站接地网实地挖掘测量计算得出,24组接地网腐蚀速率实验数据,包括土壤理化特性、接地网电阻平均增长率和接地网腐蚀速率三部分组成。土壤理化特性包括土壤含水率、电阻率、孔隙率、SO42-含量和Clˉ含量,用以表征不同接地网所处的土壤环境;接地网电阻平均增长率由接地网各支路电阻变化倍数和接地网运行时间计算得出,用以表征接地网腐蚀状态,使模型输入特征维度更加全面;接地网腐蚀速率通过截取接地网样本,利用失重法计算得出。
将24组实验数据中的前20组数据作为训练集,后4组数据作为测试集。由于6个输入维度的量纲和维度各不相同,为避免直接输入对预测模型训练速度、预测精度和模型灵敏性产生影响,文中将按照式(14)对所有输入数据[-1,1]归一化。
(14)
式中id和id′分别表示原始数据和归一化后的数据;idmax和idmin分别表示原始数据中的最大值和最小值。
2.2 模型参数设定及实验结果
UFO-BP模型中BP神经网络采用3层结构,其输入层节点数为6,分别对应输入数据的土壤含水率、电阻率、孔隙率、SO42-含量、Clˉ含量和电阻平均增长速率;输出层节点数为1,对应接地导体腐蚀速率。隐含层节点数的选取一般根据经验式(15)进行试凑,根据式(15)可知文中的隐含层节点数取值范围为[4,12],经过误差计算,确定隐含层节点数为9。
(15)
式中h、u和v分别表示隐含层、输入层和输出层节点数。
采用UFOA-BP模型对接地网腐蚀速率进行预测,同时为对比该模型的预测性能,选取FOA-BP模型、BP神经网络、ABC-SVM[14]和GRNN神经网络进行对比。设置UFOA-BP模型的最大迭代次数为200,种群规模为50,搜索半径r∈[0.1,5],学习速率为0.02,目标误差为0.000 1;FOA-BP模型的参数除搜索半径r=0.5外其余参数与UFOA-BP模型保持一致;BP模型的参数设置与UFOA-BP模型保持一致;ABC-SVM模型参数设置参照文献[14];GRNN模型中设置扩展速度为0.2。
为测试改进FOA算法的有效性,文中对UFOA算法和FOA算法的收敛曲线进行对比分析,训练收敛曲线如图4所示。
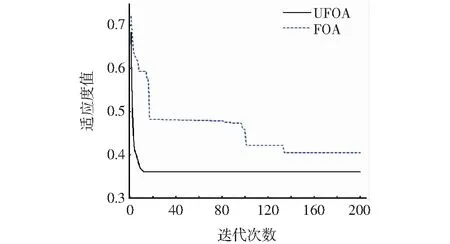
图4 UFOA和FOA收敛曲线
由图4可知,FOA算法在第134代时收敛,收敛时的最佳适应度值为0.404 9,而UFOA算法在第12代时收敛,收敛时的最佳适应度值为0.361 2。由此可以看出UFOA算法在收敛速度和收敛精度上明显优于未优化的FOA算法,验证了改进算法的有效性和可行性。
分别使用BP神经网络、FOA优化的FOA-BP神经网络以及改进FOA优化的UFOA-BP神经网络进行训练测试,得到的训练曲线如图5所示。

图5 算法训练曲线
从图5可知,使用FOA算法和UFOA算法优化后的BP神经网络达到设定误差时的训练次数由未优化的9次分别降低为6次和4次,表明使用FOA算法和UFOA算法均提高了BP神经网络的训练速度,且使用UFOA算法提升的效果更好。
使用测试集,对上述5种模型分别进行测试,预测结果如表2所示,预测误差曲线如图6所示。
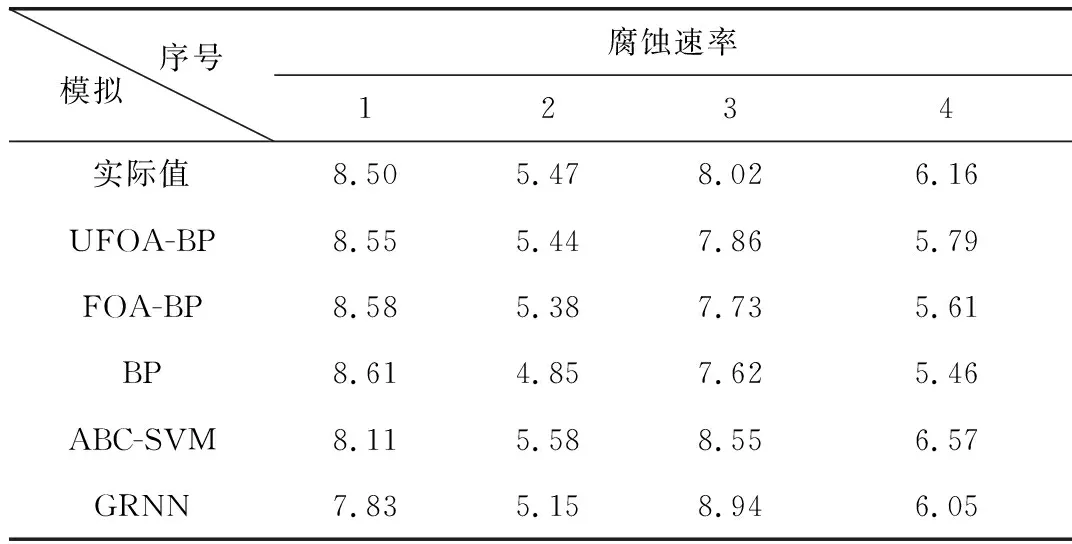
表2 5种模型预测结果对比

图6 预测误差曲线
由图6可知,使用FOA和UFOA优化后的BP神经网络预测误差绝对值之和由未优化的1.83分别降低至1.01和0.61,表明使用FOA算法和UFOA算法提高了BP神经网络的预测精度,且使用UFOA算法提升的效果更好。
2.3 预测结果分析
为了更加深入的对比5种模型的预测结果,文中从均方误差(eMSE)、平均绝对百分比误差(eMAPE)、和相对误差标准差(σMAPE)三个指标分别对5种模型的模型预测精度和模型稳定性进行评价,其评价公式如式(16)~式(18)所示。
(16)

(17)
(18)
式中m表示预测数据的个数;yi′和yi分别表示第i个数据的预测值和实际值。
分别利用式(16)~式(18)对表2中5种模型的预测结果进行分析,得到以eMSE、eMAPE和σMAPE作为评价指标的模型性能分析表,如表3所示。

表3 5种预测模型性能对比
通过表3,从预测精度的角度分析可以看出:使用UFOA优化后的BP神经网络模型预测精度相比使用FOA优化的BP神经网络模型,eMSE值和eMAPE值分别提高了0.058 8和1.5%,相比未优化的BP神经网络,eMSE值和eMAPE值分别提高了0.220 1和4.96%,且两种优化模型eMSE值均优于ABC-SVM和GRNN模型,展现了FOA算法优化BP神经网络预测接地网腐蚀速率的可行性及UFOA算法优化BP神经网络预测接地网腐蚀速率的高准确性。
从模型的稳定性和适应性角度分析可以看出:单纯的BP神经网络稳定性和适应性较差,使用FOA优化后的FOA-BP模型稳定性和适应性相较BP神经网络模型大幅提高,σMAPE值提高0.078 9,且优于GRNN模型,但FOA算法随机初始化果蝇种群位置、固定搜索半径和恒为正的气味浓度判定公式使得FOA-BP模型稳定性和适应性略低于ABC-SVM模型。针对FOA算法存在的三点不足,文中依次采用 Logistic 混沌映射、动态搜索半径策略和优化气味浓度判定值实现对 FOA算法的改进,并将其应用于BP神经网络,改进后的UFOA-BP模型稳定性和适应性在5种模型中最优。综上,UFOA-BP模型可以对接地网的腐蚀速率实现准确的预测,且模型具有较高的稳定性和适应性。
3 结束语
为了进一步提高接地网腐蚀速率的预测精度和预测稳定性,文中使用UFOA算法优化BP网络的初始权值和阈值,提出了基于UFOA-BP模型的接地网腐蚀速率预测模型,具体结论如下:
(1)利用Logistic混沌映射对果蝇群体的位置进行优化,解决随机初始化种群分布存在的不均匀和盲目性问题,提高了搜索群体的多样性和均匀性,增强了算法的稳定性;然后引入动态搜索半径策略实现算法的搜索半径自适应动态调节,提高了算法的收敛精度;最后改进FOA算法气味浓度判定公式,避免气味浓度判定值恒为正值对算法的影响,扩大了算法的搜索范围,提高了算法的预测精度,增强了算法的鲁棒性;
(2)以UFOA 中最优果蝇个体对应于BP神经网络中的初始权值与阈值,以预测值和实际值的误差绝对值之和作为UFOA的适应度函数,建立了基于UFOA-BP 模型的接地网腐蚀速率预测模型。
经过测试文中提出的UFOA-BP模型相比其他模型在接地网腐蚀速率预测中具有最高的预测精度和模型稳定性,可以满足工程的实际应用,为运维人员提前发现接地网的安全隐患并安排检修进而保障电网安全稳定运行提供帮助。

