考虑精细模型的电-气综合能源系统优化运行方法

董文杰，李俊格，田志强，孙英英，曾顺奇，艾芊

(1.东方电子股份有限公司, 山东 烟台 264000; 2.广东电网有限公司公司广州供电局, 广州 510620；3. 上海交通大学, 上海 200240)

0 引 言

近年来，随着环境污染与能源危机不断加剧，能源的高效清洁利用成为亟待解决的问题[1]。综合能源系统能够通过协调多种能源形式，实现能源的高效清洁利用[2-5]。为此，综合能源系统的优化运行成为当前能源领域的研究热点。燃气机组作为基本的电、气耦合元件，并具有排放低、爬坡速率高等优点[6]，近年来其装机容量大幅增加。燃气机组的广泛应用使电-气综合能源系统的耦合程度更加紧密[7]，也为电-气综合能源系统的联合优化运行带来了挑战。

与电力系统相比，天然气系统的动态过程缓慢，描述管道物理状态的偏微分方程难以求解，文献[8]在一定简化条件下将偏微分方程转化为代数方程；然而代数方程仍具有很强的非凸非线性特点，使得优化问题的求解难度大、收敛性无法保证。为解决天然气系统的优化求解问题，该文献提出了处理管道方程的分段线性化方法。在此基础上，文献[9-11]求解了电-气综合能源系统的联合优化问题。在电-气综合能源系统的联合优化领域，以往研究大多采用二次等式形式的Weymouth方程表征天然气管道的物理特性，文献[12]将Weymouth方程约束松弛为二阶锥约束，进而将非凸优化问题转化为凸优化问题进行求解。在此基础上，文献[13-14]采用迭代的方法进行修正以克服松弛解不可行的问题，文献[15-18]考虑了天然气管道流向未知的情况对二阶锥松弛方法进行改进。

在不同运行条件下，不同管道方程的拟合精度存在差异[19]，例如Panhandle公式适用于高压气网，而Spitzglass公式适用于低压气网。因此，Weymouth方程无法适用于所有天然气管道，否则会导致误差较大。然而，二阶锥松弛方法仅能适用于二次等式形式的Weymouth方程；分段线性化方法难以权衡分段精度与求解代价，可能导致所求运行策略不可行的问题，无法满足电-气综合能源系统的安全稳定运行要求。此外，上述文献中采用的模型还存在两点不足：(1)压缩机模型均为线性近似模型，认为压缩机功率与流入流量成正比，实际上压缩机耗气量还与首末两端压强相关；(2)电力系统模型均采用线性化的直流潮流模型或者忽略线路损耗的交流潮流模型。文献[9-18]采用了精确的数学优化算法，尽管可以得到所求模型的最优解，但是所求模型为简化模型，可能导致调度策略不可行。

为了解决模型复杂度为优化求解带来的问题，考虑从智能算法的角度寻找解决方案，以得到精确模型下的可行解。粒子群优化(Particle Swarm Optimization，PSO) 算法作为一种新兴的群体智能优化技术，适用于目前科学领域、工程领域和经济领域中很多复杂的、非凸非线性形式的优化问题。目前，PSO算法在电气工程领域有着广泛的应用[20-21]，涉及负荷经济分配[22]、无功优化[23]、最优潮流计算[24]、机组组合[25-26]、经济调度[27]等方面，并衍生出适用于特殊场景的改进算法。

随着综合能源系统逐渐成为研究热点，诸多研究将粒子群算法在电力系统中的应用方法迁移至综合能源系统领域[28]。文献[29]建立了考虑用能成本、弃风损失、负荷曲线峰谷差的多目标优化模型，研究了电-气-热综合能源系统的鲁棒优化问题。针对传统粒子群算法易陷入局部最优的问题，文献[30]将小生境技术与粒子群算法结合并提出一种非线性递减惯性权重策略。文献[31]建立了规划和运行两阶段优化模式。

在粒子群算法的应用中，为了考虑能源系统中的约束，已有文献采用的方法大致分为两种，一种是根据约束条件构造罚项并添加至评价函数中[25]，另一种是根据约束条件对结果进行检验，若不满足则采用越限代限的方法重新求解，直至满足约束条件[28]。然而，上述涉及粒子群算法应用的文献仅考虑了能量平衡和供能上下限约束，未考虑能源系统网络约束(如潮流方程约束、管道方程约束等)，可能导致调度策略不可行，出现电压、电流、压强越限等问题。

在电力系统中，根据机组出力等决策变量可以通过潮流计算得到如线路潮流、母线电压等状态变量，从而可以考虑潮流方程约束以及状态变量的上下限约束。在天然气系统中，根据气井产气量等决策变量也可以通过气网能量流计算得到如管道流量、节点压强等状态变量，从而可以考虑气网管道方程约束以及节点压强上下限约束。对于电力系统与天然气系统通过燃气轮机、电压缩机双向耦合的场景，文献[32-33]给出一种基于分别循环迭代的求解算法，通过迭代求解气网与电网得到综合能源系统的能量流分布。

在已有研究成果的基础上，文章旨在提出一种考虑电-气综合能源系统精细模型的粒子群优化方法，将电-气综合能源系统能量流计算嵌入到粒子群优化算法中，从而能够考虑较为精细的电-气综合能源系统模型。文中首先根据粒子位置得到机组出力、气井产气量，通过分别循环迭代方法迭代求解电网、气网潮流，迭代收敛后即可得到电气综合能源系统的运行状态，进而将运行上下限约束作为罚项添加到粒子的评价函数中，并赋以较高的权重，从而得到电-气综合能源系统的协同优化运行策略。

1 电-气综合能源系统协同优化运行模型

研究对象为电-气综合能源系统，其包含两个子系统，即电力网络和天然气网络，电力网络与天然气网络通过燃气轮机、电压缩机等装置耦合。由于能源系统的优化不涉及动态过程，采用精细的配电网交流潮流模型以及天然气网的稳态模型。电-气综合能源系统示意图如图1所示，文中考虑电力网络与天然气网络双向耦合的情况。

图1 电-气综合能源系统结构

1.1 电力系统约束条件

(1)常规机组和燃气机组功率约束:

(1)

(2)

(3)

(4)

(2)常规机组和燃气机组爬坡约束：

(5)

(6)

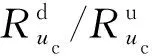
(3)母线电压约束：

(7)

(4)线路容量约束:

(8)

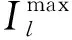
(5)线路电流约束:

(9)

该式表示线路电流与传输有功、无功功率、首端母线电压的关系。式中，plt为线路流过有功功率；qlt为线路流过无功功率；vl+t为线路首端电压；Ilt为支路电流的平方。

(6)潮流方程约束:

(10)

(11)

(12)

1.2 天然气系统约束条件

(1)天然气气井产气量约束

(13)

(2)天然气网络节点压强约束

(14)

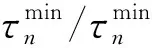
(3)天然气管道方程约束

(15)

考虑到气网的运行压力通常较高，因此采用了适用于0.7 MPa以上压力运行的高压气网Panhandle’A’公式。式中，fpt为管道流过的流量；τp+t/τp-t为管道首端、末端压强；φp为管道常数。对于其他形式的管道方程约束，所提方法依然适用。

(4)天然气网络的节点流量平衡约束：

(16)

式中(n)为与节点n相连的气井集合； (n+)/(n-)为以节点n为首端、末端节点的管道集合；(n+)/(n-)为以节点n为首端、末端节点的压缩机集合；g(n)为与节点n相连的天然气负荷集合；g(n)为与节点n相连的燃气轮机集合；Fdgt为天然气负荷流量；fugt为燃气机组耗气量；fct为流过压缩机的流量。

采用了精细化的压缩机模型，电压缩机约束如下：

(17)

(18)

式中τc-t为入口压力；τc+t为出口压力；α为多变指数并取1.27；ηc为压缩机的效率；λc为电压缩机的功率因数。考虑压缩机处于定出口压强工作状态，出口压强作为系统决策变量。

1.3 耦合约束条件

燃气轮机耗气量约束：

pugt=ηugKfugt,∀ug,t

(19)

式中ηug为燃气轮机的效率；K为天然气热值。

1.4 电-气综合能源系统的目标函数

电-气综合能源系统优化模型的目标函数即为一个调度周期内的运行成本，包括常规机组成本与气井产气成本。

(20)

2 粒子群算法及其应用

2.1 粒子群算法的应用方法

根据粒子群算法的求解流程可知，粒子群算法求解的是一个无约束优化问题，尽管可以限制粒子的位置，但仅能表示简单的决策变量上下限约束。例如，电网优化调度中机组出力为决策变量，机组出力上下限约束可以通过限制粒子在空间中的位置实现。但是，电网优化模型中还含有其他复杂约束，如潮流方程约束、机组爬坡约束、线路电流约束等，对于电-气综合能源系统优化问题亦是如此。

对于电-气综合能源系统，其决策变量即为机组有功无功出力、气井产气量、压缩机出口压强，当决策变量通过粒子位置确定时，耦合系统的运行工况即可被唯一确定，从而将各类约束作为罚项添加至粒子的评价函数中。根据现有的潮流计算方法，上述求解思路存在如下问题：

(1)从物理意义角度，机组有功无功出力、气井产气量全部由粒子位置确定，难以保证电网、气网的能量流平衡，继而无法获得耦合系统能量流分布；

(2)从计算方法角度，现有的电力系统潮流计算方法需要设定平衡节点，以平衡线路上的有功无功损失；气网潮流计算方法也需要设定平衡气井，保证全网的平衡。

针对上述问题，将电力系统中燃气机组所在节点作为平衡节点，其节点电压、相角作为决策变量由粒子位置确定；常规机组节点作为PV节点，其有功功率、节点电压作为决策变量由粒子位置确定。经过潮流计算，可以得到燃气机组的有功无功功率、常规机组的无功功率，以及全网的潮流分布。对于气网，设定某一气井作为平衡气井，其节点压强作为决策变量，其余气井的产气量、压缩机出口压强作为决策变量。经过潮流计算，可以得到平衡气井的产气量以及气网的能量流分布。电网与气网通过燃气轮机、电压缩机耦合，通过分别循环迭代算法迭代求解电网、气网能量流即可得到耦合系统的潮流分布[33]，求解方法见2.2节所示。

因此，通过给定电网、气网的决策变量，即可得到耦合系统的能量流分布，结果必然满足潮流方程约束与气网中的管道方程、节点流量平衡约束。由于平衡机组的出力、平衡气井的产气量无法通过粒子位置进行限制，只能通过添加罚项的方式进行处理。此外，爬坡约束、母线电压约束、线路容量约束、节点压强约束均需要通过添加罚项的方法进行处理。添加罚项后的目标函数如下：

(21)

式中第一项表示常规机组的发电成本和气井的产气成本；第二项表示正爬约束对应的罚项；第三项表示负爬坡约束对应的罚项；第四项表示线路功率约束对应的罚项；第五项表示全网功率平衡约束对应的罚项；第六项为气井的产气成本；第七项为节点压强约束对应的罚项，M1、M2、M3、M4、M5、M6为对应的罚因子。

2.2 电-气综合能源系统潮流计算方法

对于电-气耦合系统，考虑燃气轮机、电压缩机为耦合元件的情况，在根据决策变量求解耦合系统能量流时，为提高求解速度采用一种分别循环迭代的求解方法[33]首先假设电压缩机功率初值，然后由机组出力确定电网潮流分布，根据式(19)确定燃气机组的耗气量，求解气网潮流，根据式(17)～式(18)确定电压缩机功率作为电网负荷重新进行电力系统潮流计算，直至燃气轮机耗气量及电压缩机功率不再变化为止，计算流程如图2所示。其中，气网潮流计算采用牛顿拉夫逊法，考虑到多台燃气轮机同时作为平衡机组，电网潮流计算采用基于注入电流的多平衡节点潮流算法。

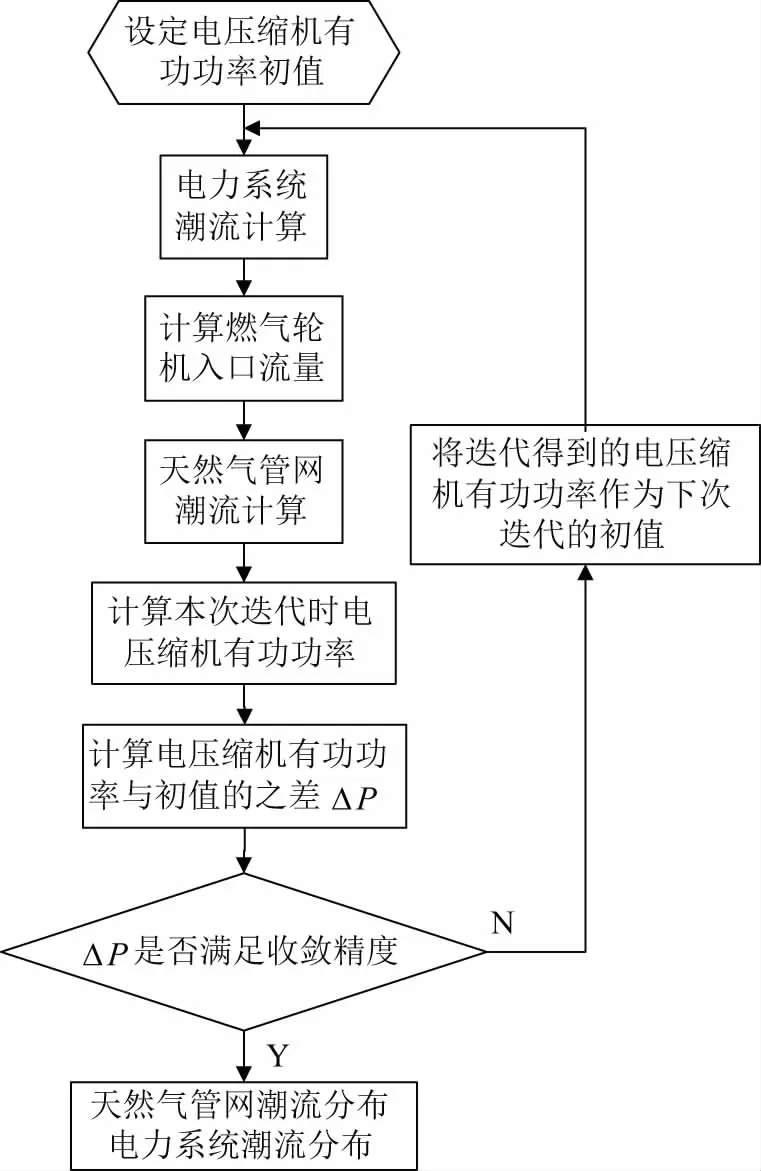
图2 电-气耦合系统能量流求解流程图

3 算例分析

为了验证优化程序的正确性，选取IEEE 13节点电力系统和7节点天然气系统通过燃气轮机、电压缩机耦合得到如图3所示电-气综合能源系统作为测试系统，测试系统及负荷参数来自文献[34]。

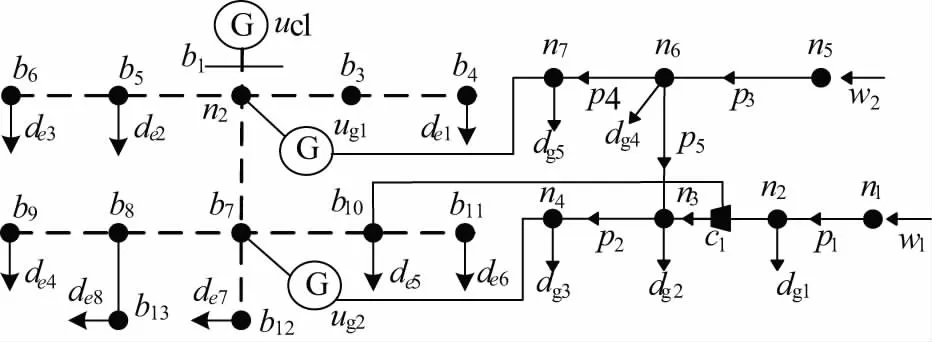
图3 测试算例拓扑图

3.1 仿真结果分析

对上述系统，取粒子种群数为100，迭代次数为200，罚系数取为20 000，得到的粒子群算法迭代曲线如图4所示，图4(a)表示不含罚项的目标函数迭代曲线，图4(b)表示含有罚项的目标函数迭代曲线，即为粒子群算法的评价函数。由图可知，含罚项的目标函数值随迭代次数增加而逐渐减小，并最终达到5.1324×106，不含罚项的目标函数值随迭代次数的变化并无明显规律，最终值5.12875×106与初值较为接近，但解的可行性得到改善。此外，迭代200次时罚项仍不为零，说明还存在部分约束越限，随着迭代次数的增大罚项5.0438×106，此时罚项较小，得到可行性更好的解。

图4 粒子群算法的迭代曲线

粒子群算法迭代1 000次后得到的机组最优出力和气井最优产气量曲线如图5与图6所示。

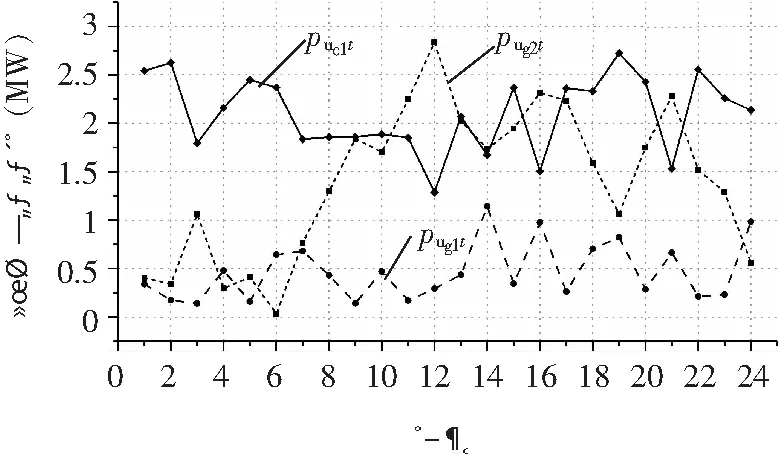
图5 机组最优出力曲线

图6 气井最优产气曲线

罚项的大小与罚系数、迭代次数、种群数量有关，增加迭代次数、种群数量也会导致计算代价的增大。在固定迭代次数为200、种群数量为100的前提下，设置不同的罚系数进行测试，测试结果如表1所示，罚项与罚系数的比值描述了约束条件的越限量。

表1 不同罚系数下的对比测试

由表1可知，当罚系数的数量级增大时，罚项与罚系数的比值先减小后出现增大的趋势，当罚系数较小时，增加罚系数的数量级有利于降低约束条件的越限量，当罚系数过大时反而引起越限量的增大。在同一数量级下，由于粒子群算法的求解结果具有一定的随机性，使得罚系数与越限量并无明显的负相关性。

为分析评价函数中各约束越限量所占比重，在罚系数取20 000、种群数取100、迭代次数取200的情况下，得到各约束越限量所占比重如图7中饼状图所示，图中未展示的约束均未产生越限。可以看到约束越限量主要集中于机组有功约束和爬坡约束中。受限于粒子群算法难以找到全局最优解，约束越限量无法完全消除，只能通过增加罚系数尽可能减少约束越限量。

图7 各约束越限量所占比例

3.2 模型对比测试分析

诸多关于粒子群算法在能源系统优化中应用的研究工作采用不考虑网络拓扑的简单模型[35-36]，也有研究工作考虑了线性化的电网模型，及直流潮流模型。这些模型虽然具有易于求解的优点，但由于简化可能导致求解结果过于乐观。为了体现考虑复杂网络模型的必要性，在相同的算例参数下，采用三种模型得到的优化结果如表2所示。其中，模型1考虑了电网的交流潮流模型以及气网稳态模型，模型2考虑了电网和直流潮流模型及气网稳态模型，模型3忽略了电网与气网的网络拓扑约束，仅考虑其中的能量平衡约束。

表2 三种模型优化结果对比

从表2中结果可知，模型1的目标函数值最大，其他模型的结果均过于乐观。主要原因在于模型3中忽略了网络拓扑约束，无法考虑线路、管道容量限制，模型2采用的直流潮流模型忽略了线路电阻及其产生的功率损耗。

与现有电-气综合能源系统优化相关文献相比[37-38]，文中采用了精细化的压缩机模型，而非假设压缩消耗功率与流入流量成正比，得到的压缩机有功功率、流入流量曲线如图8所示。由图8可知，压缩机有功功率与流入流量并非完全成正比，在某些时段功率变化趋势甚至与流量变化趋势相反。因此，考虑精细化的压缩机建模方法具有一定的意义。

4 结束语

提出了一种基于粒子群算法的电-气综合能源系统的优化方法，并考虑了精细化的电网交流潮流约束和气网稳态约束模型。为处理电网与气网中的网络拓扑约束，采用基于分别循环迭代的电-气综合能源系统潮流计算方法，根据耦合系统决策变量计算得到全网的能量流分布，继而将上下限约束作为罚项添加到目标函数中。最后，通过算例测试验证了所提求解方法的有效性，分析了罚系数对约束越限量的影响，并验证了考虑精细化模型的必要性。