改进支持向量机在电力变压器故障诊断中的应用研究

邱海枫，苏宁，田松林

(1.深圳供电局有限公司， 广东 深圳 518048；2. 南方电网深圳数字电网研究院有限公司， 广东 深圳 518034)

0 引 言

随着全球环保意识的普及，我国力争到2030年实现碳峰值，到2060年实现碳中和，这一目标促进了智能电网的发展。智能变电站是智能电网的基础，而变压器作为变电站的核心部件，其所处的环境和独特负荷往往导致故障较多[1]。故障不仅会影响供电的可靠性，而且会造成严重的经济损失[2]。对变压器进行故障诊断，可以及时发现潜在的故障，早期进行维护，具有十分重要的意义[3]。因此，对变压器故障进行准确的判断是保证电力变压器稳定、安全运行的关键。

目前，国内外许多研究者对电力变压器故障诊断方法进行了大量的研究，提出了主要气体法[4]、IEC 三比值法[5]和大卫三角法[6]等经典变压器故障诊断方法。随着机器学习的不断发展，支持向量机[7]、贝叶斯网络[8]、极限学习机[9]等一些智能算法在智能变压器故障诊断成为主流方法。在文献[10]中，提出了一种基于分步机器学习的电力变压器故障诊断模型。结果表明，与单一学习模型相比，该模型不仅具有更高的精度，而且具有更高的效率，可以有效地弥补单一学习的不足。在文献[11]中，提出了一种经验小波变换与改进卷积神经网络相结合的变压器故障智能诊断方法。结果表明，该诊断模型能有效地识别变压器的故障状态，对110 kV变压器五种典型故障的平均诊断准确率均在94 %以上。在文献[12]中，提出了一种结合蝗虫优化算法和BP神经网络的变压器故障智能诊断方法。结果表明，相比于传统故障诊断方法，改进后的方法不仅保持了网络的学习速度和全局搜索能力，而且在训练时间和诊断准确率方面都有一定的提升。在文献[13]中，提出了一种变压器故障诊断方法，该方法将深度置信网络与改进的模糊C-均值聚类相结合。结果表明，与现有的变压器故障诊断方法相比，该方法具有更高的诊断准确率，诊断准确率为93.3 %，能够较准确地识别各种变压器故障。在实际应用中，上述方法可以解决传统方法繁琐的步骤和诊断绝对化问题，但需要进一步优化训练精度和提高适应性。

在此基础上，提出了一种结合SVM[14]和BFA[15]用于电力变压器故障诊断。通过BFA的寻优能力找到最优的SVM的惩罚因子和核参数，提高SVM的故障诊断能力。通过仿真和实例进行了对比分析。

1 电力变压器故障分类

由于电力变压器结构的复杂性，在运行过程发生故障时，涉及的部位不同，具体故障类型的分类也不同[16]。常用的分类方法包括按回路分类、按变压器主体结构分类、按故障位置分类、按故障易发区分类等，具体分类方法如图1所示。

根据故障的机理和性质，可将内部故障分为两类：热性故障和电性故障，这是文中采用的主要故障分类方法。热性故障是由变压器内部局部过热引起的，根据程度的不同，过热分为低温(小于300 ℃)、中温(介于300 ℃和700 ℃)、高温(大于700 ℃)。电性故障是指绝缘材料在强电场力作用下分解产生各种特征气体或直接引起介质击穿的高能量密度故障[17]。根据程度的不同，分为局部放电、低能放电、高能放电。

图1 电力变压器故障

在现场运行条件下，热性故障和电性故障基本上是由变压器绝缘劣化引起的，故障进一步加剧了绝缘材料的劣化。因此，相关人员应采取科学有效的管理方法对运行中的变压器进行维护，及时准确地发现各种潜在障碍，延长变压器的使用寿命。

2 故障诊断模型

2.1 建立诊断模型

电力变压器通常有单一放电或热故障，对350例电力变压器故障情况进行统计分析，发现有过热和放电同时发生的情况，约占总故障量的10 %左右。因此，设置7 种故障代码，1表示正常状态，故障编码见表1。

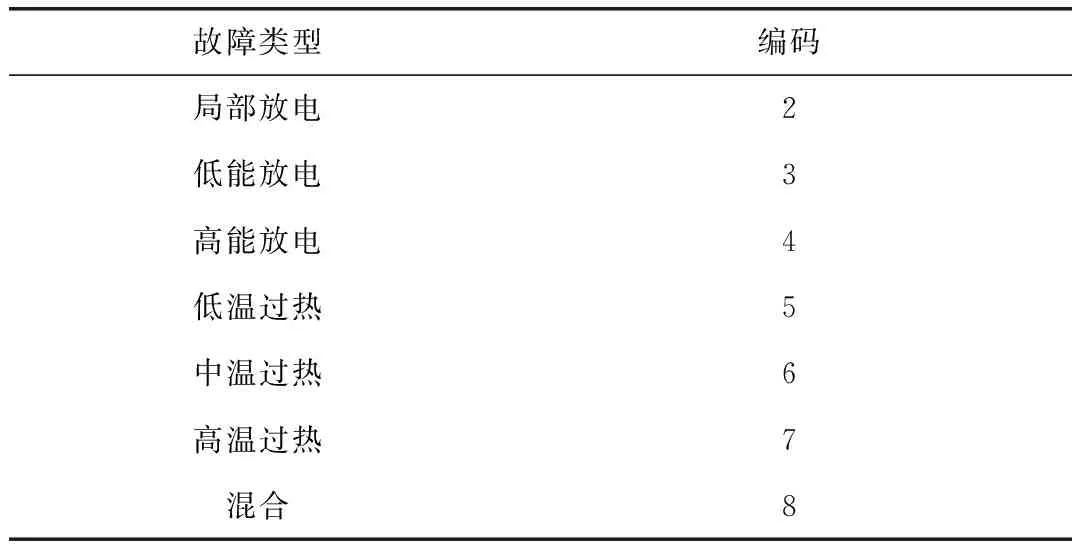
表1 故障编码

内部故障与油中气体含量相关，以C2H2、C2H4、C2H6、H2和CH4为特征量，作为输入，对输入数据进行处理，如式(1)所示[18]:

(1)

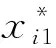
文中的SVM故障模型核函数采用RBF径向基函数，通过式(1)进行归一化为评价指标输入，以表1中的故障代码为输出,图2为诊断模型。

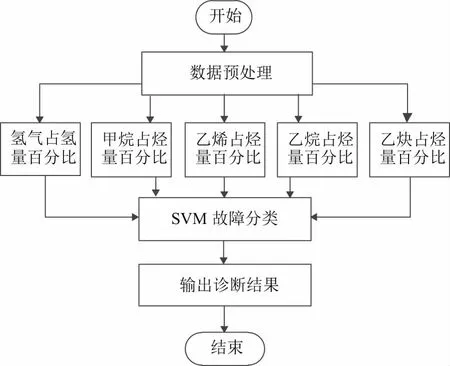
图2 诊断模型

2.2 支持向量机

支持向量机是由Vapnik等为解决小样本、非线性问题提出的机器学习方法，得到了广泛的应用(状态评估、故障诊断等)[19]。

设置一个可分样本X={xi,yi}，i=1,2,...l， 其中xi∈Rn，n为样本空间的维数；yi∈{-l,+l}为样本类别标记。如果存在最优超平面，可以将两类样本区分开，间隔达到最大。最优超平面如式(2)所示[20]:

ωx+b=0

(2)

式中ω为权重向量；b为偏差值。

通过式(3)所示约束条件进行求解。

(3)

对于线性不可分样本，最优超平面通过式(4)中的约束进行求解[21]:

(4)

式中C为控制误差的惩罚程度；ξi为松弛变量。

引入拉格朗日函数和拉格朗日乘子αi，式(4)转化为对偶问题，如式(5)所示[22]:

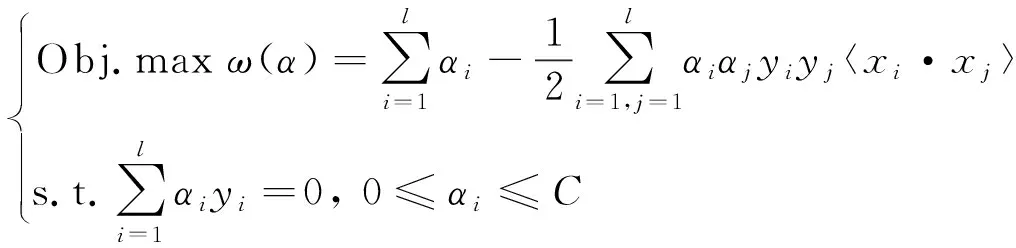
(5)

由KKT条件求解式(5)得到最优解，如式(6)所示[23]：

(6)

通过定义核函数K(xi,xj)，最优分类函数如式(7)所示：

(7)

主要将RBF核函数用于支持向量机的研究。RBF核函数如式(8)所示[24]：

K(xi,xj)=exp(-g‖xi-xj‖)2

(8)

式中g为核参数。

支持向量机模型的性能依赖于惩罚参数C和核函数的参数g的选择，参数的质量对算法的准确性有着显著的影响[25]。因此，选择BFA对SVM进行优化，以保证算法选择的参数是模型的最优参数。

2.3 改进支持向量机

BFA算法是由K.M.Passino等人提出的一种新的仿生算法[26]。通过趋化性、复制性和迁徙性三个动作实现优化。该算法由于具有群智能算法的并行搜索和易跳出局部极值等优点，应用广泛。

通过BFA的寻优能力找到最优的SVM的惩罚因子C和核参数g，使模型具有最强大的诊断能力。优化过程如下：

步骤1：对样本进行预处理，划分训练集和测试集；

步骤2：对BFA算法进行初始化，设置迁徙概率、迁徙操作次数、趋化操作次数等参数[27]；

步骤3：将{C,g}作为个体的位置坐标。初始种群细菌s个，单个细菌的位置是随机的；

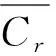
(9)

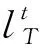
如式(10)所示，目标函数为k-交叉验证准确性最大，约束条件为{C,g}的取值范围[29]。

(10)

步骤5：求解目标函数，进行BFA操作，得到目标函数最优值，即最优的{C,g}。

步骤6：对测试样本进行故障诊断，输出诊断结果。

基于BFA-SVM的故障诊断流程图如图3所示。

图3 故障诊断流程

3 结果与分析

3.1 仿真参数

为了保证模型的效率和准确性，利用MATLAB r2018a计算并优化支持向量机的参数[30]。在对样本进行预处理后，使用libsvm 3.22工具箱对样本进行训练和测试，以获得模型的最优参数。最后，利用IBM SPSS modeler 14.1建立了支持向量机分类模型，并利用训练参数和优化参数进行分类。电力变压器故障诊断与验证。

细菌觅食算法的参数为：种群50、趋化操作次数10、迁移操作次数2、迁移概率0.25、复制操作次数44、折叠数k=10。从南方电网公司故障统计数据库中收集了320 组电力变压器故障数据。240 组训练数据(每个类别30 组)和80 组测试数据(每个类别10 组)。

3.2 仿真分析

为了证明BFA算法具有较好的优化能力，在同一样本下分别采用BFA算法和PSO算法优化SVM参数。优化过程如图4和图5所示，参数优化结果如表2所示。

图4 PSO-SVM寻优方法

图5 BFA-SVM寻优方法

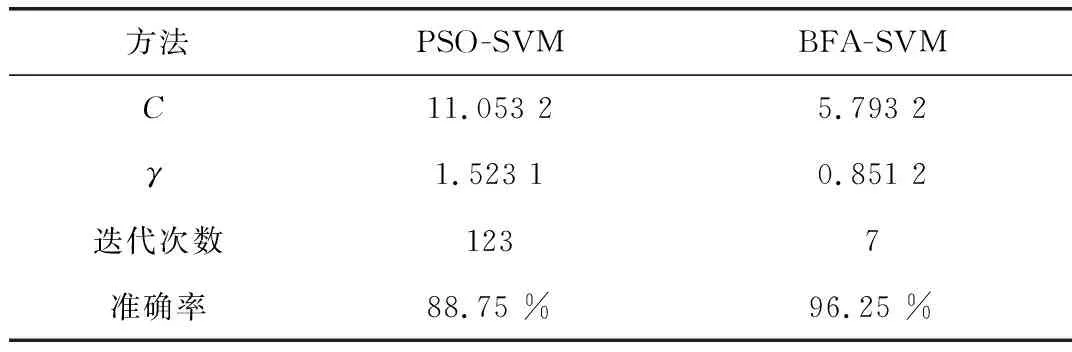
表2 不同算法参数优化结果

从图4、图5和表2可以看出，BFA的收敛速度比PSO快得多。文中模型对测试集进行诊断准确率为96.25 %。PSO-SVM模型对测试集进行诊断准确率为88.75 %。因此，BFA算法相比于PSO算法具有一定的优势。

由图5的优化过程可以看出。由于算法开始时初始菌群较大，可以快速找到最优适应度，但在优化过程中初始菌群分布较广，且菌群个体间存在明显差异，平均适应度差异很大，在首次复制(10 次迭代前)，50 %的不相容个体死亡，剩余适应度较好的被复制。因此，菌群的适应度得到了显著提高。使波动不那么明显，慢慢趋于平缓。迁徙操作， 40 次迭代后，细菌位置发生变化，跳出局部极值。在经过趋化和复制操作，达到最优适应度。

为了证明基于BFA-SVM的电力变压器故障诊断模型比未改进前的SVM电力变压器故障诊断模型具有更好的分类性能，图6所示优化前模型的诊断结果。图7所示优化后模型的诊断结果。

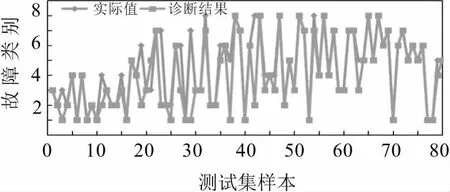
图6 SVM模型测试集诊断结果

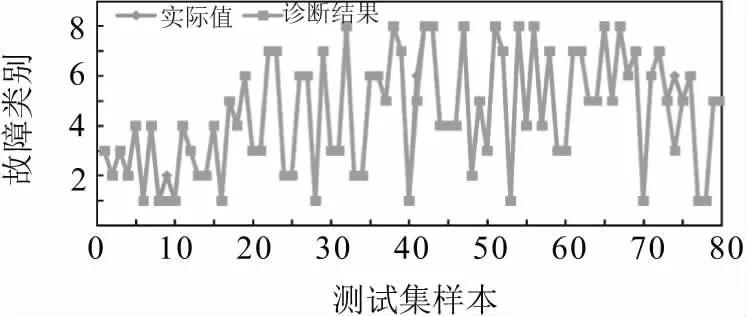
图7 文中模型测试集诊断结果

由图6可以看出，未改进前SVM模型参数C和g是系统设置的默认值。结果表明，该诊断模型在测试集的分类结果中有17 个错误，准确率为78.75 %。

由图7可以看出，基于BFA-SVM诊断模型，测试集的诊断结果表明，该模型分类结果仅错误了3 个，准确率为96.25 %。

以上仿真结果表明，基于BFA-SVM的故障诊断模型相比于改进前具有更好的分类功能、准确性、鲁棒性和寻优能力等。

3.3 实例分析

变电站中电力变压器发生短路故障(型号为sfz11-31500/110)，对变压器油进行色谱分析。采用本文故障诊断模型判断，诊断故障代码为4(高能放电)，色谱数据见表3。

为了确保变压器的安全运行，将变压器送回工厂进行维护。研究发现，短路冲击会造成变压器内产生高能放电，导致铜外露和绝缘烧损。在低压C相存在绕组和铁心融化现象。表明绕组在铁心处有高能放电。文中建立模型诊断结果与变压器的实际情况相符。

表3 色谱数据

4 结束语

文章提出将SVM和BFA结合用于电力变压器故障诊断。采用BFA优化SVM的惩罚因子和核参数，提高了SVM的故障诊断能力。结果表明，BFA在选择SVM的最优参数方面优于PSO，故障诊断从优化前的88.75 %提高到优化后的96.25 %。所提模型具有优良的分类能力、良好的鲁棒性和较强的寻优能力。由于目前实验室硬件和数据规模的影响，故障诊断模型还处于初级阶段。基于此，模型的持续改进将是下一步的重点。