NMPC算法下六自由度机械臂避障轨迹规划
乔栋豪,仲志丹,张浩博,赵耀
(河南科技大学机电工程学院,河南洛阳 471003)
0 前言
随着现代化生产的高速发展,机械臂成为了不可或缺的生产工具,在各个领域中都出现了机械臂的身影。机械臂在制造市场中的需求量连年增加,对其要求也越来越多,工作环境也更加复杂。对于六自由度机械臂来说,如何在复杂的环境中实现路径规划及避障是一个技术性难题。
关于机械臂避障方法的研究有很多,常见的有DONG和DU[1]提出的通过计算机械臂工作空间密度,进而得到机械臂在有多个障碍物复杂环境中的无碰撞路径,并通过仿真验证了该方法的可行性;LIU等[2]提出了一种以圆柱包围盒模型作为检测手段,通过将理想轨迹进行分段处理,把每段轨迹的中间点作为参数,并对参数进行优化达到避障目的的方法。这种基于圆柱包围盒模型的机械臂避障算法在对机械臂进行碰撞检测时也较为常见。ISMAIL等[3]将动态避障算法应用于缆索串联机械臂,在保证执行器缆索张力有界的前提下,寻找最短最快的避障路径。此外,经典的避障算法还有人工势场法,在机器人的运行环境中加入了引力场;快速随机搜索树算法(RRT)[4],可以快速搜索空间当中没有障碍的路径;概率路线图法(PRM)[5],是基于图搜索的方法。上述这些算法能够计算出机械臂最优或次优轨迹,但是计算量较大,无法对动态变化做出快速反应,同时无法将机械臂的轨迹优化和运动学优化联系在一起。虽然后来CHEN等[6]采用分段描述机械臂轨迹,并通过优化各段轨迹中间点选取的方法,在保证避障的同时对运动控制进行优化,但机械臂在运动过程中需要在中间点停顿,不符合实际应用需求。国内对于机械臂轨迹规划的研究很多,尤其机械臂的安全问题是一个主要研究方向,其中碰撞检测[7]和运动控制[8-9]都有很大的进展,但是关于机械臂自主避障的研究相对较少。
非线性模型预测控制(Nonlinear Model Predictive Control, NMPC)[10]方法对系统模型不确定性具有较强的鲁棒性,在控制相关领域[11]已经有了广泛应用,同时对非线性系统控制效果明显,是解决机械臂轨迹规划问题的有效手段。NMPC控制算法是将复杂的问题分为多个阶段,通过滚动优化策略,逐步得到每个阶段的最优解,减少了计算的复杂性,对动态环境适应能力强,因此该方法也可以用于解决机械臂动态避障问题。该控制算法也曾被应用于移动机器人的轨迹跟踪过程中,表现出良好的控制效果。
如今机械臂轨迹规划研究中大多数使用PID控制与强化学习相结合,使得机械臂能够按照预定轨迹运动并实现自主避障。NMPC控制算法与其他算法相比更适用于六自由度机械臂这种复杂的非线性控制系统,在运动过程中,运动的轨迹精度、响应速度、对扰动的抑制能力都有明显提升,在避障过程省去强化学习中间训练环节,节约时间的同时保证机械臂不会在训练中受到灾难性的损坏。
本文作者在以上研究的基础上提出一种基于NMPC六自由度机械臂避障轨迹规划算法。首先对六自由度机械臂建立动力学模型,然后通过使用圆柱包络法对机械臂与障碍物间距离进行判断,当判断机械臂与障碍物相撞冲突时,以最小的代价实现冲突消解,同时使得机械臂快速重回预定轨迹,最后通过MATLAB对机械臂防撞控制进行仿真。仿真结果表明,该算法能够使得机械臂在保证运动稳定前提下完成自主避障。
1 机械臂动力学模型
六自由度机械在工业生产中应用较广,其系统构造也极其复杂。在对机械臂进行运动仿真和控制算法的设计过程中,机械臂动力学模型的推导至关重要。常见机械臂建模方法有许多种,此次采用拉格朗日公式法建立系统模型。
简化拉格朗日方程可以推导出机械臂的动力学方程,形式如下:
(1)
用矢量形式表达,机械臂输入约束如下:
τmin≤τ≤τmax
(2)
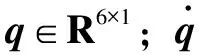
2 碰撞检测方案设计
此次设计采用圆柱包络法进行碰撞检测,用适当高度和直径的圆柱将机械臂和待测障碍物包裹起来,通过这种方法,把空间中的物体碰撞问题简化为两个圆柱之间的位置关系的计算问题,当障碍物进入机械臂的探测范围时,通过计算两个圆柱之间的距离,判断机械臂和障碍物发生碰撞的可能性。两圆柱之间的位置关系如图1所示。
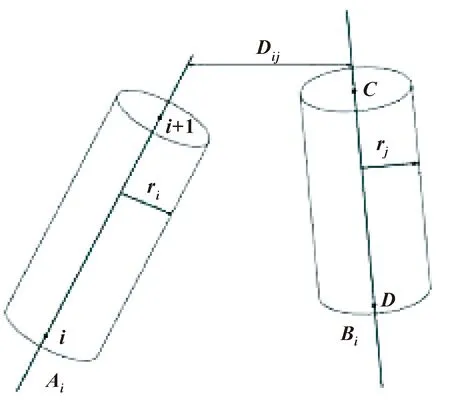
图1 两圆柱之间的位置关系
在图1中,圆柱体Ai和Bi分别是对机械臂和空间中遇到的障碍进行简化后得到的模型,C为圆柱表面的圆心,两个圆柱体半径分别为ri和rj。对于圆柱体Ai来说,用O(x0,y0,z0)表示其质心的坐标,那么(xi,yi,zi)和(xi+1,yi+1,zi+1)则表示该圆柱体上下两端面的坐标,该圆柱体Ai轴线方程表示如下:
(3)
m=xi+1-xi,n=yi+1-yi,p=zi+1-zi
(4)
对方程进行简化可得:
Li=[Xi(t),Yi(t),Zi(t)]=[xi,yi,zi]+t[m,n,p]
(5)
通过相同的方法,也可以计算出圆柱体Bi轴线所处直线的方程为
Lj=[Xj(t),Yj(t),Zj(t)]=[xj,yj,zj]+t×[u,v,w]
(6)
其中:t∈(0,1)。
那么两轴线间的垂直距离为
(7)
若两圆柱体轴线间的垂直距离Dij小于两圆柱体半径之和ri+rj,则表示机械臂存在碰撞风险,需要启动避障控制,规划新的轨迹;反之则表示不会与障碍物发生碰撞。
3 机械臂自主防撞最优控制模型
当判断机械臂和障碍物将要发生碰撞冲突时,机械臂需要进行自主控制实现冲突消解。在该过程中需要使机械臂以最小代价避开障碍物,然后继续沿着预定轨迹运动。
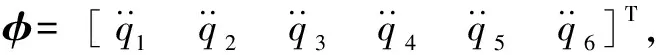
(8)
其中:φ(tf)为距离代价函数,为tf时刻机械臂末端到达结束点远近程度;R为单位矩阵。定义tf时刻机械臂转角位置向量为
Xu=
[q1(tf)q2(tf)q3(tf)q4(tf)q5(tf)q6(tf)]
目标位置为
Xc=[q1q2q3q4q5q6]
Q为单位矩阵,则φ(tf)可改写为
φ(tf)=[Xu(tf)-Xc]TQ[Xu(tf)-Xc]
(9)
φTRφ为机械臂防撞过程中的能量代价,g(t)为防撞代价,定义为
(10)
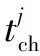
(11)
联立上述各式,机械臂自主防撞最优控制模型如下:
(12)
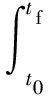
通过求解该非线性优化模型,可以得到机械臂规避障碍物成功到达目标位置的最优驱动力矩τ(i)。但是,对于六自由度机械臂复杂的非线性模型来讲,庞大的计算量难以保证避障过程中的时效性。为此,需要对模型进行离散处理,分步求得每一步的最优控制结果。
4 基于NMPC机械臂防撞控制算法
4.1 线性化处理
采用常用的泰勒公式展开法进行输入输出线性化处理[12-13],通过该方法提高计算效率。在模型的线性化处理过程中引入滚动优化策略,实时优化机械臂的空间状态模型,保证线性化模型正确的同时增强了系统的鲁棒性。
对机械臂的状态变量进行定义:
则机械臂连续状态空间方程为
(13)
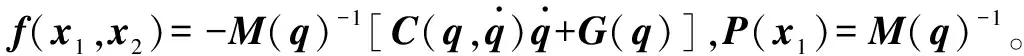
通过利用泰勒公式展开得到离散化系统模型如下:
(14)
其中:
C=[I6O6×6]
x(0)=[x1x2]T,x(i)表示机械臂在第i个采样时刻的预测输出,x1、x2分别表示位置和速度。
4.2 控制约束
在以式(14)为系统预测模型的基础上提出了一种新的轨迹跟踪控制器的设计方法,通过这种方法可以减小机械臂预测输出和实际输出之间的偏差,当偏差到达最小时为最优控制率。对最优控制率评价的性能指标如下:
(15)
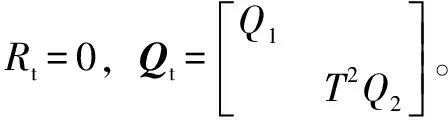
τ=Kxref+Fx(t)+D
(16)
其中:x(t)=[x1x2]为当前时刻系统状态。
D=-M(x1)f(x1,x2)
4.3 轨迹约束
机械臂沿着预定轨迹运动过程中,如果遇到障碍物,应当使得机械臂能够自主制定新的轨迹,绕开障碍物,然后重新快速回到预定轨迹上来。在满足控制约束的前提下,机械臂轨迹约束控制器设计如下:
(17)
(18)
(19)
τmin≤Kxopt(1)+Fxs+D≤τmax
(20)
τmin≤Kxopt(i+1)+Fxopt(i)+D≤τmax
(21)
其中:J=(X-Xd)TQ(X-Xd)T+ΔUTRΔUT;xs为机械臂系统在当前时刻的状态;τold记录上一时刻输出力矩。
通过式(16)可以计算得到K、F、D的值,代入上述各式当中,保证机械臂在预测时域内预测输出满足各个力矩约束条件。同时在计算得到机械臂的最优控制增量后,可以计算出机械臂下一时刻的期望轨迹xopt(1)。由于机械臂各关节转动存在范围约束,记为qmax和qmin,则期望轨迹应满足:
qmin≤xopt1(i)≤qmaxi=1,…,N
4.4 机械臂动机决策
机械臂在避障过程当中,对算法的时效性要求较高。由于六自由度机械臂系统复杂,对搜索空间进行剪切可以帮助快速找到最优避障策略,减少计算量。文中定义5种防撞机动策略,U、D、L、R、C,分别为机械臂以最大转动速率向上、下、左、右转动以及呆在原地5种方式。
上述5种策略构成了机械臂的可选机动策略集合E={U,D,L,R,C},并且每一控制量:
对于每层预测时域都有5条分支数,当预测时域为N时,分支数为5N。随着预测时域增大,计算量也不断增加,需要对动机决策树进行减枝进而减少计算量。
机械臂在避障过程中逐渐向结束点靠近,在每一层预测时域中,代价函数J应逐渐减小,在k时刻应满足以下关系:
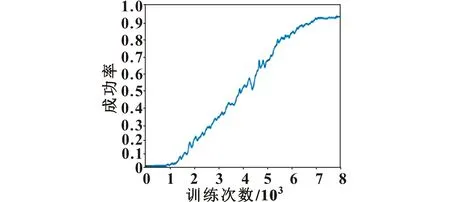
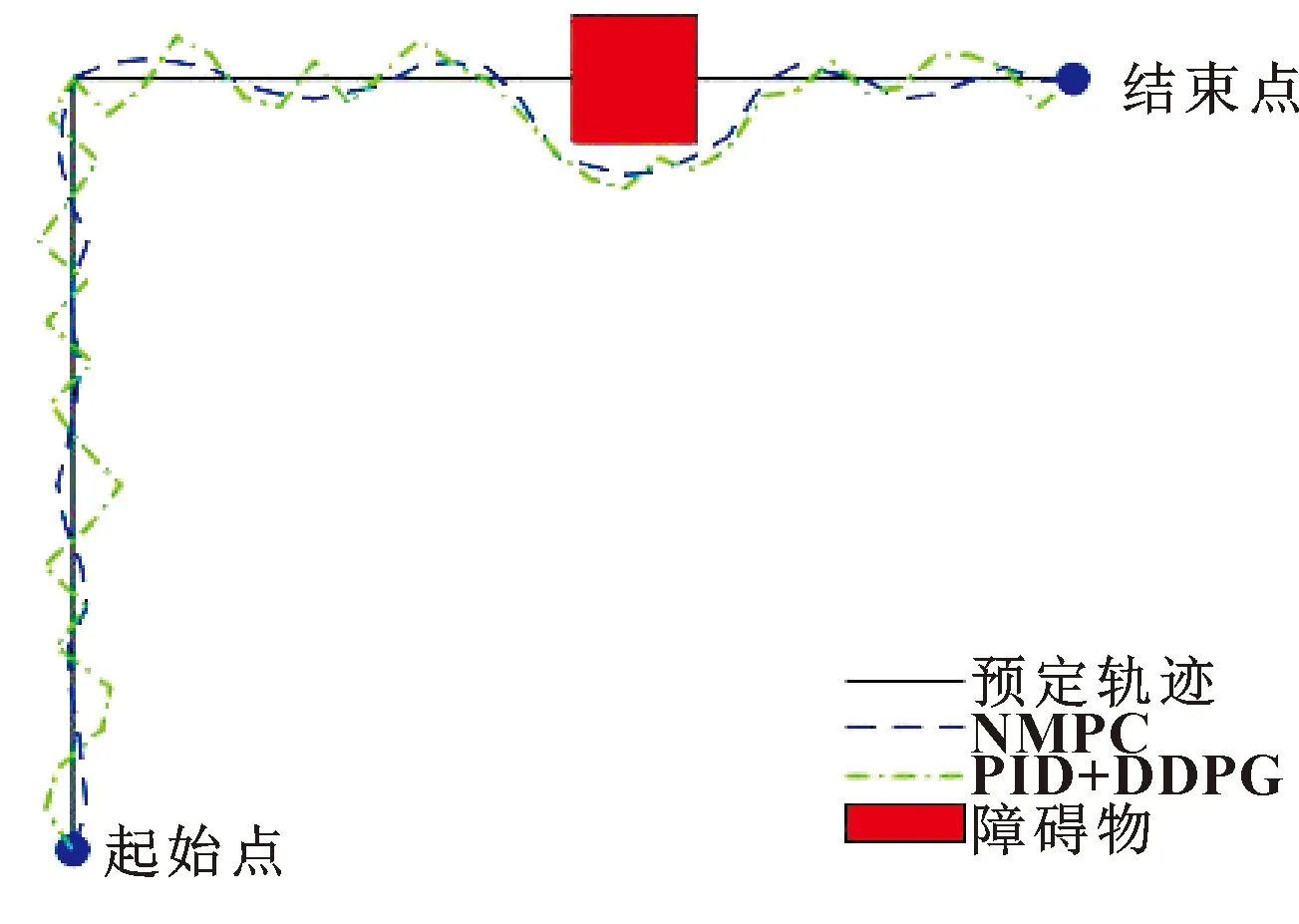
Jk(τ) (22) 式中:φ(x(k|k))为当前位置x(k|k)的终端代价。 令U*(k)为机械臂在k时刻计算得到的最优控制序列,则在k+1时刻控制序列为 (23) 综上所述,建立基于NMPC的六自由度机械臂避障轨迹规划算法,如下所示: 第一步,设定圆柱包络法中圆柱半径为dm,对预测时域、采样周期、各个加权参数进行初始化设置,同时确立5种动机策略的对应值。 最后,令k=k+1,返回步骤1,循环执行。 通过MATLAB Robotics Toolbox(version 10.1)工具箱来对机械臂避障算法进行仿真验证,同时与PID和强化学习组成的控制避障算法的效果进行对比。其中强化学习选用较为先进的DDPG算法[14]进行实验,该算法具有训练速度快、准确率高的特点。 采用PUMU560机械臂作为控制对象,该机械臂的相关参数信息可以参考文献[15]。通过MATLAB Robotics Toolbox(version 10.1)搭建模型,如图2所示。 图2 MATLAB中PUMU560机械臂模型 在空间中指定起始点和结束点,同时给出预定轨迹,将机械臂末端当作成一个点,可以观测到在二维平面中机械臂在误差允许的范围内,沿着预定轨迹运动,如图3所示。可以明显看出:机械臂末端在NMPC算法下运动更准确,误差较小,效果更好。 图3 机械臂未遇到障碍物运行轨迹 通过观测机械臂在约束条件下转动位置、角速度、角加速度3个物理量来判断机械臂在避障过程中的稳定性。在实验运动过程中,第二关节转动幅度最大,因此对其转动角度、角速度、角加速度进行分析,具体变化如图4所示。 图4 机械臂转动过程中第二关节角位置、角速度、角加速度图像 从图4可以看出随着运动的进行,机械臂在两种控制算法下都可以到达指定位置,但是相对于图(b)中的PID控制,图(a)中在NMPC算法控制下,机械臂运动过程连续平滑,角速度、角加速度没有出现跳点,关节、运动部件运行更加平稳。因此通过与PID算法对比可以发现,机械臂在响应速度,控制精度以及抗扰动等方面,NMPC算法的控制效果更好。 在避障过程中,强化学习DDPG算法需要提前进行训练,其训练次数与成功率的关系如图5所示。可以看出:当训练次数达到7 000次时,避障成功率在90%以上,随后再增加训练次数,成功率不再明显增加,一直趋近平稳。选用训练7 000次后的DDPG算法进行避障实验。 图5 DDPG算法下机械臂避障成功率 在预定轨迹中加入障碍物,机械臂在两种算法下都可以提前对障碍物进行规避,然后重新回到预定轨迹,到达结束点,如图6所示。 图6 机械臂进行避障运动轨迹 随后再反复多次进行实验,发现机械臂在强化学习算法下会偶尔出现避障失败的情况,然而NMPC算法却能保证机械臂每次都能成功避开障碍物,到达结束点。通过对比可以发现,NMPC算法不但省去了训练过程,同时在避障的成功率上更有保证。 通过对NMPC算法进行改进,将其应用在六自由度机械臂的轨迹规划当中进而达到空间避障的效果。通过采用圆柱包络法对机械臂周围存在的障碍物进行碰撞检测,同时为了减少计算量,将复杂的机械臂系统进行了线性化处理。在机械臂动力学模型中加入控制约束和轨迹约束,保证了运动精度与系统稳定性。在机械臂避障过程中加入动机决策,减少了搜索范围,提高了避障的时效性。通过MATLAB仿真显示,机械臂实际轨迹与预定轨迹近似一致,当遇到障碍物时,可以避开障碍物然后重新回到预定轨迹,到达结束点。同时与PID+DDPG算法进行对比,结果表明NMPC控制效果更好,而且机械臂动态避障的成功率更高。但是NMPC算法的计算量较大,在未来的研究中会对该算法进行进一步优化。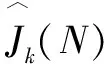
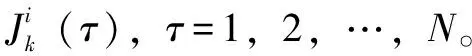
5 仿真实验分析
5.1 搭建仿真环境
5.2 仿真结果分析
6 结论

