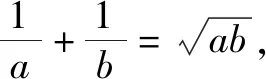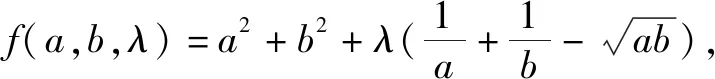一题多解探思路 追本溯源挖题根

浙江省绍兴市越州中学 屠丰庆

吉林省北华大学数学与统计学院 屠蕊林

数学解题不能仅满足于一道题的答案，而应通过探索思考.去追求更优、更快捷的解题方法.“一题多解”就是从不同角度、按不同思路、用不同方法给出同一道题的解答.

但同时，著名数学家陈景润先生在谈起数学解题时，曾说过“题有千变，贵在有根”[1].以题根方式展开教学，抓住解题思维入口，才能帮助学生理解问题本质，总结归纳解题过程，以不变应万变.笔者以2021年浙江数学高考17题为例，在一题多解的基础上，追本溯源，挖掘此类考题的题根，给出解决问题的捷径，以期对学生快速解题有所帮助.

1 一题多解，探析思路

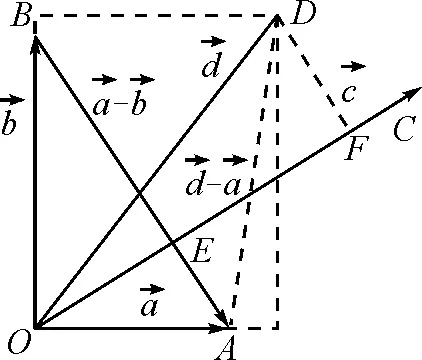
图1

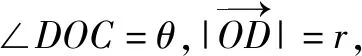
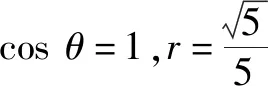
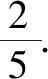
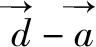
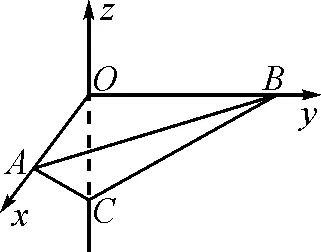
图2

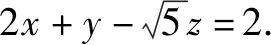
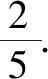
点评：思路4揭示了转换后问题的几何意义，将代数下的条件和目标转化为平面方程和空间距离，使得问题更直观[3].最后类比初中三角形中用面积法求高的方法，利用体积相等求得结果，也不难被一般的高中生接受.

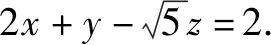
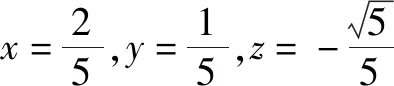
点评：利用偏导求极值(最值)的方法，有较深的高等数学背景，大学教材中称之为“拉格朗日乘数法”.此方法在解决条件极值时，在本质上观点“高屋建瓴”，在范围上“普遍适用”，在过程上计算“可程序化”.面对技巧性较高的题，读者不妨用此法一试，往往会有“柳暗花明又一村”之感.

2 追本溯源，挖掘题根

为便于理解，以二元变量为例，具体介绍拉格朗日乘数法涵义的初等理解和解题过程.

问题在约束条件h(x,y)=0下，求z=g(x,y)的最值.

(1)函数f(x,y,λ)=g(x,y)+λh(x,y)的涵义解释.由约束条件h(x,y)=0，可知f(x,y,λ)=g(x,y)+λh(x,y)=g(x,y)与线性规划类似，不妨称之为目标函数，其中λ可以理解为目标z=g(x,y)在约束条件h(x,y)=0下可自由伸缩的空间，不妨称之为调节系数.问题就转化为：通过不断调节λ，使得f(x,y,λ)=g(x,y)=z取到极(最)值.

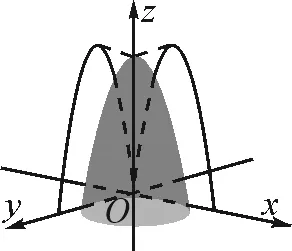
图3

(2)关于“偏导”，可以这么理解：对于目标函数f(x,y,λ)=g(x,y)+λh(x,y)，问题在几何上就是求空间坐标系中曲面的最高(低)点相应的函数值，如图3所示.求目标函数关于x，y的最值，可以分步实施，先将y看成常数，求关于x的极值，再将x看成常数，求关于y的极值.某种意义上，可以理解为将曲面分别向xOz，yOz坐标平面作正投影，曲面最高(低)点对应投影曲线上的最高(低)点，此处取得极值，因而两个偏导都应该等于零.

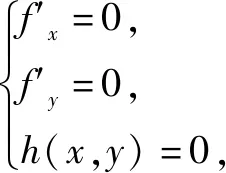
3 举一反三，速解考题

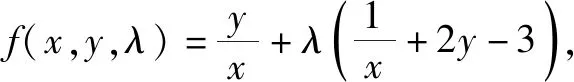
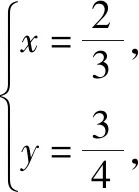
例3(2020江苏高考，题12)已知x,y∈R，5x2y2+y4=1，则x2+y2的最小值是.

解析:令f(x,y,λ)=x2+y2+λ(5x2y2+y4-1)，分别关于x，y求偏导得到方程组

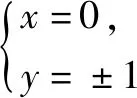
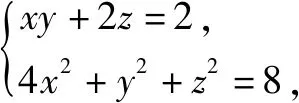
解析:令f(x,y,z,λ,μ)=xyz+λ(xy+2z-2)+μ(4x2+y2+z2-8),分别关于x，y,z求偏导得到方程组

经消元检验，可知