同构法在解析几何中的应用举例*

福建省莆田第一中学 林 敏

在解析几何的相关问题的解决过程中，我们经常会遇到多个形式类似、变量不同的方程，如果只关注单一方程的求解，运算将会变得较为冗长而复杂，这时我们不妨采用同构的思想，将形式相同的方程统一起来，从整体上分析他们所体现的规律，再根据其规律寻找运算结果，化繁为简，获得较为简洁的代数结果，对应更为直接的几何规律.

当今的教育改革之下，教育的目标直指素养的形成，需学生明确重要的基础知识，理解最简洁核心的数学原理，形成最切实有效的数学思想.这就需要教育者引导学生去发现数学的内在驱动力，透过现象探求本质，学会思考和分析.

1 利用同构解决圆锥曲线的切线的相关问题

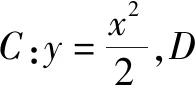
分析：题目中给出的条件为过D作C的两条切线，解决问题的一条思维路径是设出过点D的直线方程，利用直线和抛物线相切的位置关系，得到A，B两个点坐标的表示，然后获得直线AB的方程，这样就能够根据方程的形式得出所过定点的坐标.但是直接表示出来还是较为复杂的，所以应当注意变量之间的关系，利用同构形式巧妙解决问题.第二条思维路径是从切点入手，表示出该点处的切线的方程，两条切线都过同一个点D，则点D的坐标适合两条直线的方程，利用解与方程关系的转化获取直线AB的方程，进而得到定点坐标.

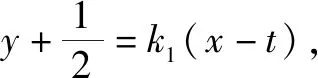
解析1侧重使用切线的斜率进行运算，找出斜率满足的方程，“设而不求”，从同构的角度，获得了两斜率满足的关系式，表示出目标直线的方程，进而得到直线所过的定点坐标.该题中由于此抛物线可看作函数的图象，所以可借助于函数求导来解决相关切线的问题，再利用同构即可解决问题．

解析2也可以从切点入手，先利用导数得到曲线在点A和B处的切线方程，然后将点D代入两切线方程之中，得到上面的两个式子，再利用方程与解的关系转换为直线AB的方程形式.利用这种同构的想法，可以快速得到曲线的切割线方程，解法简洁明了．

规律总结：根据上面同构的想法，可以总结出圆锥曲线的切割线的统一结论，它们都是数学中形式对称而优美的式子，比如对于抛物线y2=2px(p>0)，过点(x0,y0)作它的两条切线，切点所在直线的方程即为y0y=px+px0，可以看作把点的坐标融入抛物线的标准方程从而得到切割线的方程，给人以美的感受.当然，对于椭圆和双曲线，也有对应的结论，这里就不再赘述了．

熟练应用：

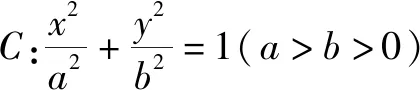
(Ⅰ)求椭圆C的标准方程；

(Ⅱ)若动点P(x0,y0)为椭圆外一点，且过点P的椭圆C的两条切线相互垂直，求点P的轨迹方程．

分析：本题也涉及到圆锥曲线的切线问题，且需由切线垂直推导动点P的轨迹方程，解题思路和上题类似，先探寻切线斜率满足的关系式，再根据垂直关系获得动点坐标满足的方程．

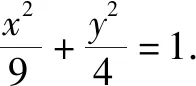
(Ⅱ)①先考虑特殊位置，即两切线一条斜率为0，另一条斜率不存在时，P的坐标为(±3,±2).

②一般情形下，切线斜率都存在，设过点P(x0,y0)的直线方程为y-y0=k(x-x0)，与椭圆方程联立消y，得(9k2+4)x2+18(y0-kx0)kx+9(y0-kx0)2-36=0.

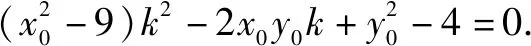
综上可知，动点P的轨迹方程为x2+y2=13．

2 利用同构解决圆锥曲线的内接三角形相关问题

例2(2021全国甲卷理第20题)抛物线C的顶点为坐标原点O，焦点在x轴上，直线l:x=1交C于P，Q两点，且OP⊥OQ．已知点M(2,0)，且⊙M与l相切．

(Ⅰ)求C，⊙M的方程；

(Ⅱ)设A1，A2，A3是C上的三个点，直线A1A2，A1A3均与⊙M相切．判断直线A2A3与⊙M的位置关系，并说明理由．

分析：本题中涉及到抛物线内接三角形共内切圆的证明，由于在抛物线上取了三个点，所以涉及到的变量比较多，此时一定要抓住主变量和从变量，利用地位平等的变量满足关系的同构形式去解决问题．

解析：(Ⅰ)抛物线C的方程为y2=x；⊙M的方程为(x-2)2+y2=1.

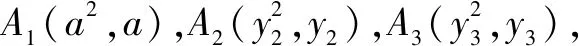
在本题的解决过程中，抓住坐标与直线方程的关系，注重运算过程中出现的同构形式，充分利用同构，将解与方程进行一定的转化利用，最终比较简洁地处理了问题，又能够给人以对称整齐的感受，可谓数学的精妙所在.所以，在学习的过程中一定要注意观察，总结规律，不可一味地陷入盲目的复杂运算中无法自拔，一定要多从思维的深刻性上下功夫，才能达到学精的目的．

熟练应用：

图1

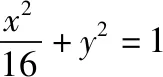
(Ⅰ)求圆G的半径r；

(Ⅱ)过点M(0,1)作圆G的两条切线交椭圆于E，F两点，证明：直线EF与圆G相切．

分析：与例2类似，圆固定，点动，证明相切的位置关系，但是情境由抛物线变为椭圆之后，运算上会稍复杂，可以尝试完成该题．

3 利用同构解决圆锥曲线有关参数的问题

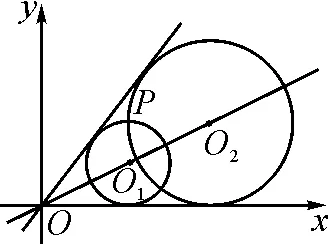
图2

例3如图2所示，在平面直角坐标系xOy中，圆O1、圆O2都与直线l:y=kx及x轴正半轴相切，若两圆的半径之积为2，两圆的一个交点为P(2,2)，求直线l的方程.

分析：题中给出两个圆的半径之积，参考韦达定理，考虑半径之和，则需构造两半径满足的方程，即找出r1与r2的某种统一之处，体现图形的对称性与方程形式上的统一．

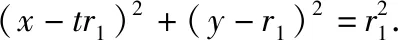
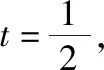
反思：两圆交于同一定点，且结构相似，圆的方程是二次结构，将定点坐标分别代入两圆的方程，统一起来即得同一方程的两根即为两个变量，也就是这其中蕴含着两个变量间完整的关系.若作差得到两圆公共弦所在的直线方程，则破坏了圆方程的结构，将定点坐标代入直线方程也只是得到一个孤立的式子，不能全面反映所需信息，导致此题无法继续求解，而利用同构式则可柳暗花明.

同构的思想是培养数学核心素养的一种参考和媒介，学生对同构的认知与应用反应出学生能否用数学的眼光去观察世界，能否用数学的方法去解决遇到的问题，是素养的体现.当然本文只是同构法在一个方面的呈现，更多同构的应用还有待挖掘.