数学教学中渗透数学思想的几点体会

新疆昌吉州育林中学 成东平

中学数学中的数学思想有公理化的思想，符号化的思想，等等.一般认为，在中学数学教学中，应使学生学会和熟悉的数学思想有:化归与转化的思想，函数与方程的思想，分类讨论思想，数形结合的思想.在中学阶段进行数学思想教学，有两条基本途径，即第一条是逐步渗透，第二条是强化训练.下面重点谈一谈笔者在渗透数学思想方面的一些体会.

1 充分挖掘数学思想，在教学中进行渗透

理论教学与解题教学是中学数学教学的两条主线，数学思想的教学应贯穿于这两条主线之中[1].由于学生对数学思想从了解到认识，从理解到掌握应用，需经历较长的时间，而且解题教学更侧重于数学思想的应用，因此我们必须把数学知识的教学过程作为渗透数学思想的主渠道，充分挖掘教材中基础知识部分蕴含的数学思想，尽可能创造较多的机会展现数学思想，以便学生在掌握知识的同时，逐步感知、理解数学思想的真谛.

例如，立体几何中多面体与旋转体直观图的画法，其实是借助于平面图形来刻画空间图形，通过“展开图”将柱体、锥体、台体的侧面置于某平面，把空间曲面的面积转化为平面图形的面积来计算……这些看似平淡的内容，无不体现着转化思想——空间问题平面化，教学中若因其简单而忽视，就会失去渗透数学思想的良机.

2 精心设计教学过程，使数学思想渗透其中

渗透，即依附其上，隐含其中.渗透是指教者有心，学者无意的方式，是一个根据教学内容，反复、逐步进行的过程.渗透数学思想不是简单地给学生灌输一些名词，数学思想的渗透应自然贯穿于教学过程之中，让学生在获取知识、掌握方法的过程中自然地受到数学思想的熏陶，达到一定火候后经老师点拨逐渐形成关于数学的基本观点——数学思想[2].因此,教师应精心设计教学过程，充分暴露知识的发生、发展过程和解题探索过程中的思维轨迹，并引导学生积极参与这一过程，让学生在参与中亲身感知数学思想.

例如关于“祖暅原理”的教学，笔者设计了如下的教学过程.首先问学生以前学过哪些几何体体积的计算公式，接着提出问题:“现有一块形状不规则的小石块，你如何才能测得其体积?”当学生通过探究，得出“将小石块投入盛水的量筒里，观察水面升高了多少，计算出升高部分水的体积”的解决方法后，又提出问题:“这一解决问题的过程中蕴含了一种很重要的数学思想，你能说出它是什么吗?”有的学生说阿基米德定律，有的学生说体积相等原理……虽答不到点子上，但大多有一种比较朴素的认识，在此基础上老师适时点拨：将不规则小石块的体积求解问题，转化为圆柱体积的问题，此即化归思想.之后，又拿出一把扑克牌，将其叠堆成长方体形状再扭曲变形成斜平行六面体，让学生思考变形前后体积是否相等，提出祖暅原理，不仅使化归思想贯穿于探索问题的思维过程之中，而且使学生明白了祖暅原理的作用，为其后体积公式的推导留下伏笔.

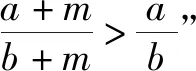
3 揭示数学方法内涵，深化对数学思想的理解

数学思想源于数学知识和数学方法，在教学中揭示数学方法的内涵，既可以使学生对运用数学思想处理问题的具体操作方式得到更多的了解，也可以让学生从思想的高度认识数学方法，深化其对数学思想的理解.

4 有计划、有步骤地实施渗透

要渗透数学思想，必须深入分析教材，逐一析出各部分内容中蕴含的数学思想，并根据学生的实际知识层次、认识水平制订出一个切实可行的计划，何时、何处渗透何种思想，确定渗透的侧重点，充分挖掘教材潜力，反复多次进行渗透，使学生在一系列的潜移默化中逐步领悟数学思想.

例如，在“复数”的教学中，有着渗透化归思想的良好条件.因此，在此单元的教学中，笔者将化归与转化思想的渗透作为数学思想教学的侧重点，在具体教学方式上，除在复数的概念、复数的表示形式、复数的运算等内容中逐步渗透化归思想外，还利用一题多解突出对学生进行化归意识的培养.比如课本中有这样一道题：“已知z1,z2∈C,z1z2=0，求证z1,z2中至少有一个是0.”引导学生从下面几种思路去解答.

思路1：设复数的代数式.设z1=a1+b1i，z2=a2+b2i(a1,b1,a2,b2∈R).

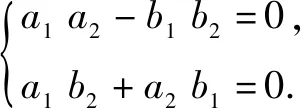
思路2：取模法.由z1z2=0，得|z1||z2|=0.

所以z1，z2至少有一个为0.

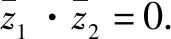
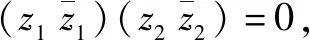
故z1，z2中至少有一个为0.

通过这三种解法的归纳，学生不难发现其相同的思想实质——复数问题实数化，而无论是“代数形式”“取模法”，还是“共轭法”都是化归的手段.一题多解使学生对化归思想有了较为充分的认识.

渗透，是数学思想教学的初级阶段，当学生已初步形成数学思想时，就应当提供条件让其在数学活动的实践中进一步去领会、去掌握[3].比如，学生在解题时总是将分式问题整式化、无理问题有理化、多元问题一元化、复数问题实数化、空间问题平面化……，在这一系列具体实践中，学生一旦悟出未知化已知、复杂化简单的规律其实就已初步具备了化归与转化的思想.从这个意义上讲，渗透与应用是数学思想教学的两条基本途径，关于如何在应用中强化学生对数学思想的认识，作为数学思想教学的另一侧重点，在这里笔者不作叙述.