基于R-Vine Copula函数的极端降水联合分布模型及风险识别

曾文颖，徐明庆，宋松柏，吴昊昊

(1.西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100； 2.西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌 712100； 3.西北农林科技大学经济管理学院，陕西 杨凌 712100)

全球气候变暖加速水文循环，引起降水、蒸发、对流层水汽、径流等要素发生变化[1]，导致洪水、干旱和热带风暴等极端水文事件频发和加剧[2-3]。由于极端降水突发性强、破坏性大，对社会安全及自然环境造成严重影响[4]，尤其对人口密集的城市，暴雨、大雪和冰雹等极端降水天气影响更大，如2021年河南特大暴雨事件作为强降水致灾的典型，对人民生命和财产造成了巨大损失。在气象监测中有效识别致灾性极端降水，对雨洪管理、工程设防标准、灾情预警预报等具有重要意义[5]。

风险事件发生的概率常用数理统计法和水文频率法计算。Smith等[6-7]通过描述连续空间内极值事件的相关性，发现Max-stable模型可以很好地揭示水文气象极值事件的空间结构与特征；陈星任等[8]采用Pearson相关分析和双侧t检验，分析了1961—2018年中国持续极端降水事件的发生频次、持续日数、总降水量以及极值的变化规律，探讨了环流因素对这些变化的影响，发现中国持续极端降水事件的频率、强度及其对总降水的贡献率均呈现出增大的趋势；郑江禹等[9]从降水量级、降水频率及发生时间等方面系统分析了珠江流域年、雨季及旱季3个时间尺度上的极端降水特征，探讨了极端降水变化特征的机理；刘曾美等[10]采用定性分析法和概率风险分析法，分析了中珠联围暴雨与承泄区磨刀门水道的上游西江马口站的洪水遭遇规律；王辉等[11]对昆明市极端降水事件时空演变特征、严重程度及城市效应进行了定量分析，发现昆明市极端降水严重程度以及城市化对其影响效应将不断加剧。极端降水作为水文极值事件，内部属性要素互相关联[12]，计算极端降水多因子联合概率分布，刻画指标间存在的不同尾部相关性，深入分析相关性规律，有助于提高灾害综合危险性评估准确度。

早期水文的多变量分析主要采用多变量正态分布、对数正态分布、Gumbel分布等方法[13]，这些传统边缘分布分析方法通常基于变量线性相关的假设，而实际水文变量可能服从正态或偏态分布，准确构建非线性与非正态的多变量联合分布是当前研究的热点和难点[14]。Copula函数可以提供可靠的多变量边缘分布连接方式，被de Michele等[15]引入降水相关研究，而后Zellou等[16]基于双变量Joe Copula模型对降水和潮位的遭遇风险及城市危险性进行了分析。但当考虑更多指标及其相关性结构时，Copula函数的参数求解随建模维度增加变得更加复杂，缺乏灵活性和通用性。

为解决高维Copula函数的求解问题，Bedford等[17]引入Vine图形化思想，通过构建多元条件相依结构，利用Pair Copula函数将多元联合分布分解，从而建立Vine Copula模型。常见的C-Vine适合描述有主导变量的相关结构，D-Vine适合描述有临近关系的结构，均需要对变量之间的相关性作严格假设[18]，遍历性弱[19]。如何建立适合于高维随机变量的Vine Copula函数来评估极端降水因子之间的联合分布情况并进行风险分析，找到敏感因子及其对极端降水事件的联合响应，还需要进一步研究。

本文选用灵活且条件独立要求弱化的R-Vine Copula函数[20]构建极端降水联合分布模型进行风险分析，识别致灾性敏感因子，并以河南省4个气象站的实测数据进行模型验证和对比分析，以期对极端降水事件的风险管控提供参考。

1 模型构建

1.1 边缘分布函数

在进行极端降水指标边缘分布拟合时，为消除评价指标之间的量纲差异，需对数据进行归一化处理[21]。选取常用的伽马分布(Gamma)、正态分布(Normal)、韦伯分布(Weibull)、广义极值分布(generalized extreme value，GEV)和对数逻辑分布(log-logistic，LL)5种传统分布函数[22-23]，以极大似然法(MLE)估计参数，通过拟合优度检验，选出描述极端降水指标分布规律最优分布线型，建立边缘分布。

1.2 R-Vine Copula函数

Copula函数作为边缘分布函数与多维联合分布函数之间的纽带，是描述变量间相依性的一种有效工具[24]。假设u=FX(x)和v=FY(y)分别为连续随机变量X和Y的累计概率分布函数，由Sklar定理知，随机变量X和Y的Copula联合分布函数为[25]

P(X≤x,Y≤y)=C(FX(x),FY(y);θ)=

C(u,v;θ)

(1)

式中θ为衡量边缘分布之间相关性的Copula参数。

常见的Copula函数类型有Gaussian、Student-t、Clayton、Frank、Gumbel 和Joe等[26]。不同类型Copula函数适用于拟合不同尾部分布特性的序列，其中Gaussian Copula函数尾部渐近独立，具备零尾部相关性；Student-tCopula函数具备较厚尾部特性，对变量间尾部相关关系较为敏感；Joe Copula函数具有明显的下尾相关性；Frank Copula函数适合刻画具有对称尾部相关性的变量；Gumbel Copula函数对变量分布的上尾部变化比较敏感，能够捕捉到上尾相关的变化；Clayton Copula函数对变量分布的下尾部变化比较敏感，能够捕捉到下尾相关的变化。

综合不同Copula函数的特点，结合图论和条件函数，建立由节点、树和边组成且具备复杂多因子联合分析能力的R-Vine Copula模型，其中每个节点代表一个变量yi，节点间的连线称为边，代表由所连接2个节点组成的Pair Copula函数，后续每一棵树的节点都来自其前一棵树的边[27]，则n维R-Vine Copula函数的密度函数为[28]

(2)

式中：cje,ke|De为边e对应的Pair Copula密度函数；yDe为由条件集De决定的条件向量；yje、yke分别为节点je和ke处的变量；F(yje|yDe)、F(yke|yDe)为条件分布函数；n为节点数；e为任意边；Ei为边的集合；je、ke分别为边e的两个节点；De为je和ke间的连接条件集。

当维数较小时可以遍历搜索所有Vine结构，但随着维数的升高，Vine结构呈指数增长，求解难度大、可操作性不强[29]。为此，结合TSP(traveling salesperson problem)[30]算法，调用R语言中的TSP包，以每级树赤池信息准则(AIC)之和最小为依据，优选每个节点处的Copula函数类型并计算参数值。

1.3 基于R-Vine Copula函数的极端降水联合分布模型

基于R-Vine Copula函数的极端降水联合分布模型(以下简称“R-Vine Copula模型”)构建及风险识别的主要步骤为：①分别建立各极端降水指标的边缘分布函数，根据KS检验、CvM检验和均方根误差进行边缘分布函数优选，计算原始样本点处的函数值；②将所选指标两两组合成二维数组，以Gaussian Copula、Student-tCopula和Frank Copula，以及Clayton Copula、Gumbel Copula和Joe Copula的0°、90°、180°、270°旋转式(记Clayton Copula的0°旋转式为Clayton0°)，共15种Copula函数共同构建一级树；③以AIC加和值最小为定量评价指标，通过TSP算法和极大似然法选取一级树的最优Copula函数并计算其参数；④二级及以上的拓扑结构将受到前一级的制约，即上一级树的一个边对应于下一级树的一个节点，重复建立一级树，直至选出二级树的最优Pair Copula类型及其参数；⑤重复上述过程，生成所有树的拓扑结构，完成R-Vine Copula模型的构建；⑥以原始数据均值作为基准值，分别按照不同概率分布(0.1、0.3、0.5、0.7、0.9)，改变其中一个极端降水因子的值，计算联合概率密度值，进行风险识别。

2 模型验证和对比分析

2.1 研究区域与数据来源

河南省年平均降水量为600～1 200 mm，淮河以南为1 000～1 200 mm，黄淮之间为700～900 mm，豫北地区为600～700 mm，年降水量区域分布不均，具有从东南向西北减少的趋势。温带大陆性季风气候的不稳定性，造成年际降水量差别明显，主要表现为极值比大、变差系数较大以及年际丰枯变化频繁等。选取河南省郑州、新乡、驻马店和南阳4个气象站实测数据对模型进行验证和对比分析。根据中国气象数据网的中国地面气候资料日值数据集，搜集4个站点1958—2017年日降水量数据，计算国际通用的4个极端降水指标(大于1 mm年降水总量PT、年降水强度PS(总降水量与降水日数比值)、最大1 d降水量R1和连续5 d最大降水量R5)，绘制各气象站点PT、R1和R5序列如图1所示。1958—2017年郑州站年平均降水量为626.65 mm，最高可达1 028.2 mm；新乡站在2016年出现日降水量达414 mm的特大降水；驻马店站年平均降水量为948.78 mm，最高可达1 780.3 mm，1975年和1982年最高日降水量大于400 mm，降水量充沛；南阳站年平均降水量为769.07 mm，最高可达1 434.5 mm。总体来看，年降水量在空间分布上由东南向西北逐渐减少，且南部暴雨发生概率高于北部。

(a) 郑州站

2.2 边缘分布优选

以水文中常用的Gamma、Normal、Weibull、GEV和LL 5种不同类型分布函数，对归一化处理后的极端降水指标进行经验分布和理论分布拟合，采用极大似然法估计参数，通过均方根误差(RMSE)和KS检验进行边缘分布优选。在优选边缘分布时，以假设检验的概率P>0.05、两个分布间最大距离D<0.16为临界值，判断分布是否可行。以P值接近1、D和RMSE最小为优选标准，综合考虑3个指标选出不同气象站不同指标的最优分布函数，结果如表1所示。由表1可见，除郑州站和驻马店站的PT和PS以及南阳站的R1指标外，其余均服从GEV分布；4个气象站R1和R5指标中有87.5%服从GEV分布。由于GEV分布从原数据极值中抽样，而非依赖原数据概率分布特征，对具有极值的气象数据边缘分布拟合较为合理。

表1 极端降水指标边缘分布函数优选Table 1 Optimization of edge distribution function of extreme precipitation indices

2.3 联合分布的建立

由优选的边缘分布，计算样本点的函数值，代入R-Vine Copula模型中，求解各个连接点处的最优Copula函数类型及其参数，通过AIC值、KS检验和CvM检验与C-Vine Copula模型(基于C-Vine Copula函数构建的极端降水联合分布模型)进行对比，结果如表2所示。R-Vine Copula和C-Vine Copula模型的KS检验P值均大于0.89，CvM检验的P值都接近1，能较好地拟合4个变量之间的联合分布，模型具有合理性。对比两种模型的优劣发现，对于郑州站和驻马店站，R-Vine Copula模型的KS检验更优，南阳站R-Vine Copula模型无论KS检验还是AIC值均优于C-Vine Copula模型。整体而言R-Vine Copula模型拟合效果更佳，充分描述了不同变量之间的尾部特征，且无须对数据相依性结构做出预先假设，具有更高的灵活性。

将求解的R-Vine Copula模型各节点Pair Copula函数类型和参数列于表3，以南阳站为例，建立的一级树中，PT和PS、PT和R1选用Gaussian Copula连接，变量之间渐近独立，呈现零尾部相关；R1和R5之间具有上尾相关特性，R1的增减直接影响到R5，在一级树的基础上，利用最大生成树原理，继续生成二级树，其中“R1,PS;PT”和“R5,PT;R1”之间主要为对称尾部相关，通过Frank Copula函数建立三级树。根据计算结果绘制R-Vine结构示意图如图2所示。

对R-Vine Copula模型进行检验，随机生成100组数据，计算PT、PS、R1、R5两两之间的Kendall和Spearman相关系数，以新乡站和驻马店站为例，绘制箱体图如图3和图4所示。新乡站模拟产生的PT-PS、PT-R1、PS-R1、R1-R5的Kendall相关系数的箱图中线与原序列接近，其他因子间的Spearman相关系数也分布在箱体的上下四分位数之间。而驻马店站除PS-R1在箱体上下误差线之间，其他指标均落在箱体的上下四分位数之间。对图3进行分析可以发现，无论是新乡站还是驻马店站，PT-PS和R1-R5之间具有较大的相关性，可以认为年降水量与降水强度、最大1d降水量与最大5 d降水量的概率分布密切相关，在发生气象灾害时，会出现联合响应。总体而言，R-Vine Copula模型模拟生成的样本较好地保持了原序列的Kendall相关系数和Spearman相关系数，拟合结果贴近实测值，因此所构建的模型可用于分析研究区极端降水指标的联合概率分布情况。

表2 R-Vine Copula和C-Vine Copula模型检验结果Table 2 Test results of R-Vine Copula and C-Vine Copula model

表3 R-Vine Copula模型各节点函数选择和参数估计Table 3 Function selection and parameter estimation at each node of R-Vine Copula model

图2 南阳站R-Vine结构及参数示意图Fig.2 Schematic diagram of R-Vine structure and parameters at Nanyang station

2.4 风险识别分析

为分析极端降水指标PT、PS、R1、R5对极端降水事件联合风险的影响，以原始序列的均值作为基准值，采用R-Vine Copula模型计算不同概率分布(0.1、0.3、0.5、0.7、0.9)对应指标值，结果见表4。

在各因子处于同一概率分布时，其对应联合概率密度值越大，说明该因子对联合分布变化率的影响越大，即联合风险对其越敏感[26]。通过改变关键风险因子的值，用R-Vine Copula模型计算联合概率密度的具体方法为：4个极端降水因子中，以其中之一作为关键风险因子，另3个因子为非关键风险因子，关键风险因子取概率分布为0.1、0.3、0.5、0.7和0.9时的统计值，非关键风险因子取实测序列的均值来计算联合概率密度，结果如图5所示。对于郑州站，当R5取概率分布0.3、R1取0.5时，对应的联合概率密度值较大，认为郑州站的极端降水多因子联合概率密度主要受到R1和R5的影响，其对联合分布变化率的影响最大。对于新乡站和南阳站，PS的概率分布取0.1时，对应的联合概率密度值最大，概率分布从0.1变化到0.9的过程中，PS从最敏感因子变为敏感性最弱的因子，因此在工程施工安全设计及极端降水灾害防范过程中，概率分布为0.1～0.3的PS值应重点考虑。对于驻马店站，各因子对联合分布产生影响主要集中在概率分布为0.1～0.3之间，其中PS的概率分布取0.3时，对联合分布变化率影响最大。

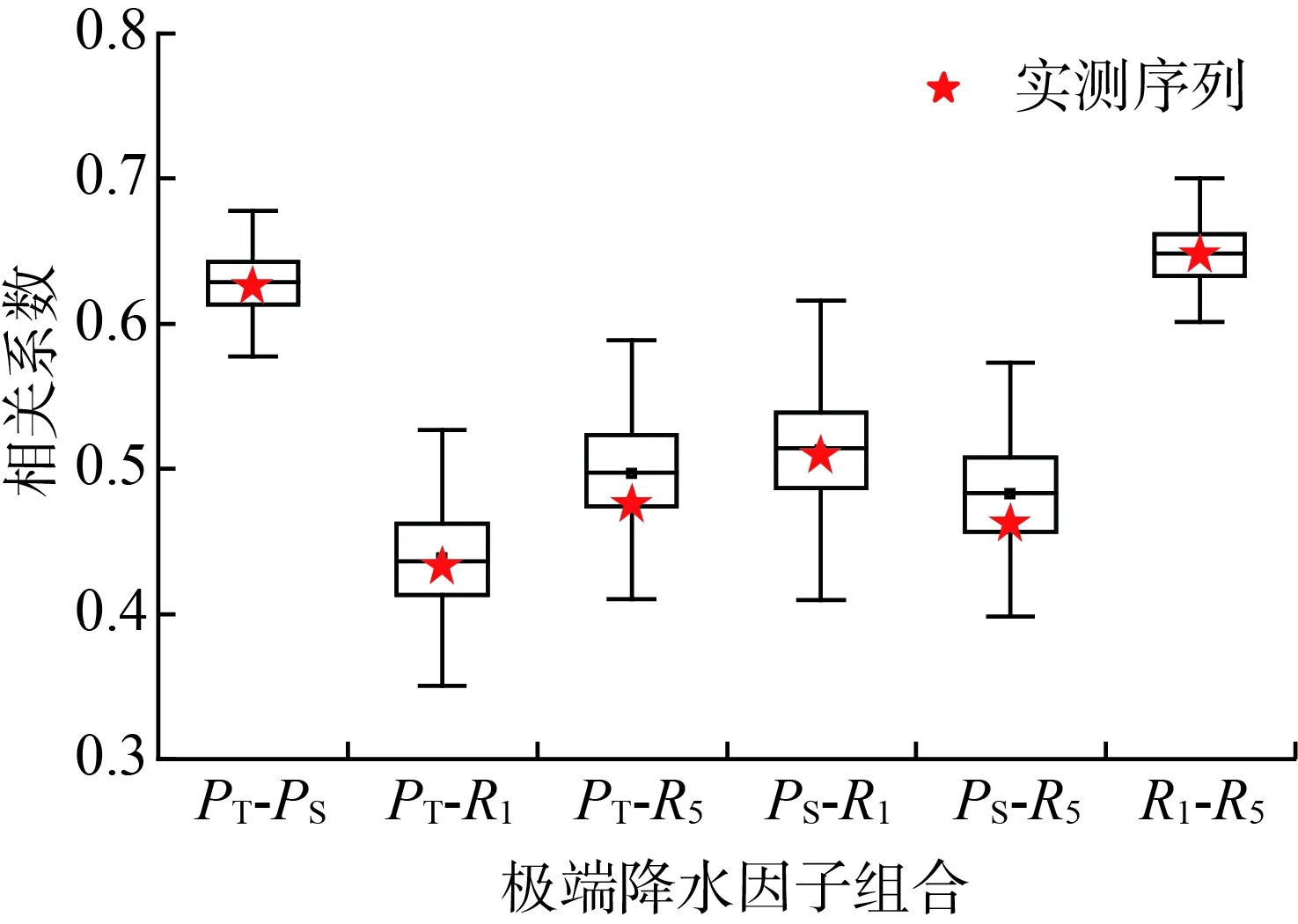
(a) Kendall相关系数

(a) Kendall相关系数

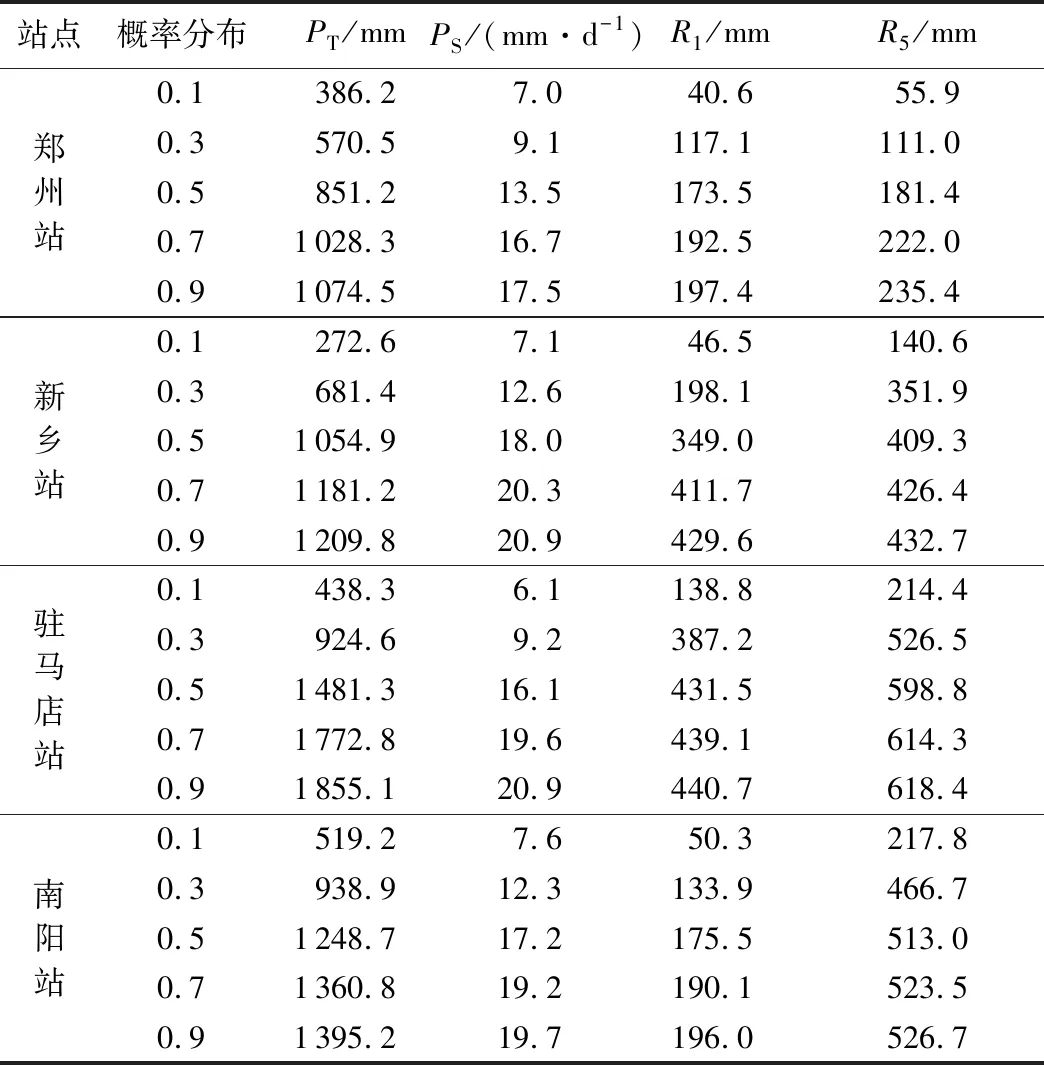
表4 不同概率分布的极端降水指标值Table 4 Extreme precipitation indices with different probability distributions

根据风险识别结果，得出对郑州站联合概率密度影响最大的因子为R1和R5，新乡站、驻马店站和南阳站则是PT和PS。图6是其他指标为50%概率分布时，联合概率密度对敏感因子的联合响应分布图，可见联合概率密度随敏感因子的概率分布值增大而增大，在敏感因子概率分布值为0.4～0.6附近达到最大，后又随敏感因子的概率分布值增大而减小，两个敏感因子对联合概率密度的影响呈现正相关关系。

3 结 语

本文构建了基于R-Vine Copula函数的极端降水联合分布模型，该模型无须对数据的相关性结构做出预先假设，具有更高的灵活性。河南省极端降水联合分布模拟对比结果表明，该模型可以描述变量之间不同的尾部特征，较好地保持了原序列的Kendall和Spearman相关系数等统计特征，可用于分析极端降水指标的联合概率分布。应用该模型识别了河南省极端降水风险，结果表明：年降水总量PT与年降水强度PS、最大1 d降水量R1与最大5 d降水量R5概率分布呈现密切相关关系；郑州站的极端降水多因子联合概率密度主要受R5和R1影响；新乡站和南阳站的PS随概率分布增大由最敏感因子降为最不敏感因子；驻马店站各因子对联合分布产生影响主要集中在概率分布为0.1～0.3时，且PS的概率分布取0.3时影响最大。

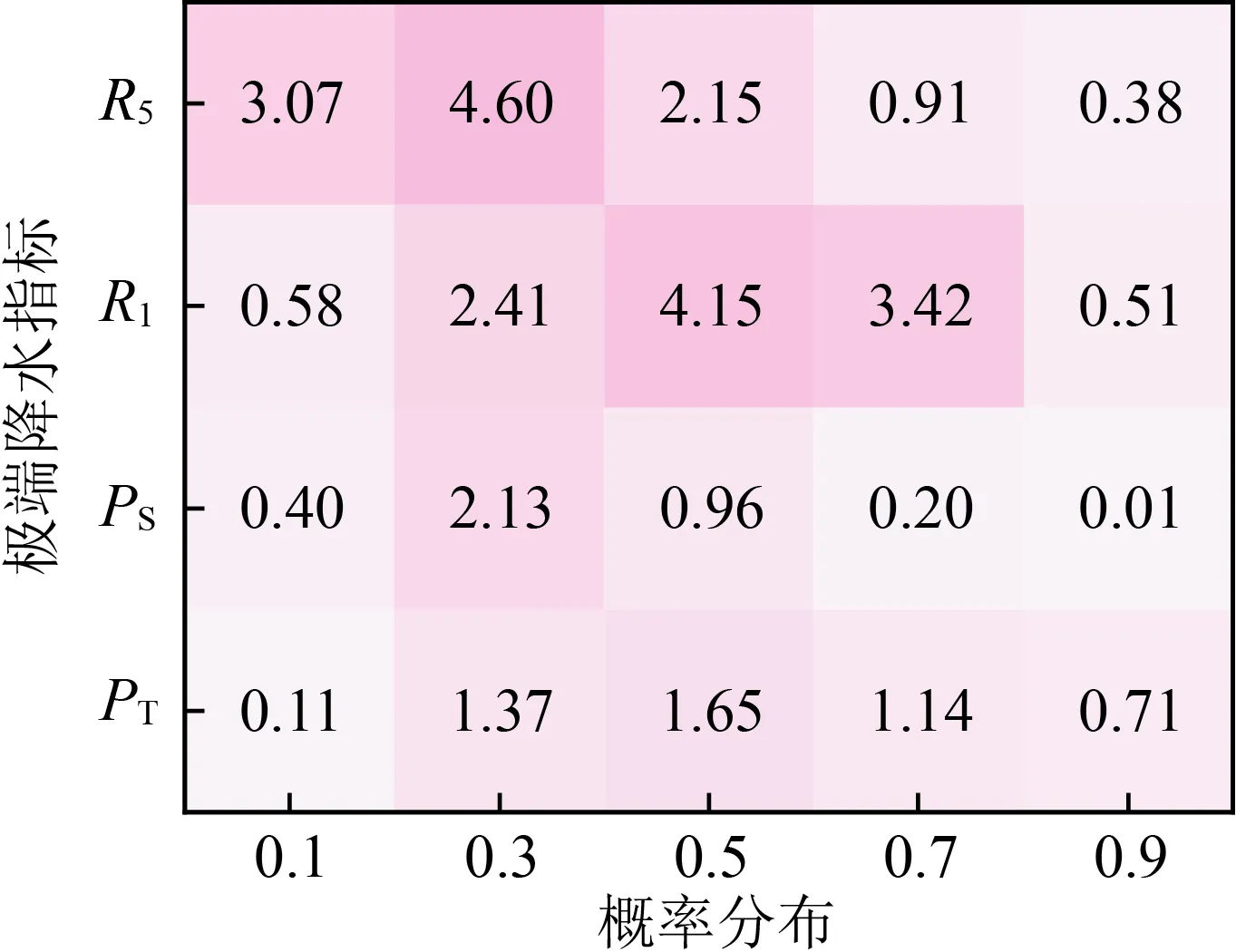
(a) 郑州站

(a) 郑州站