灰绿耦合雨洪系统多目标优化建模与应用

2022-11-22 00:22李江云胡子欣

水资源保护 2022年6期

李江云，李瑶，胡子欣

(武汉大学土木建筑工程学院，湖北武汉 430072)

城市内涝频发和雨水径流引发的面源污染带来了一系列的水安全和水环境问题，灰色和绿色基础设施是解决前述问题的有效手段[1-2]。灰色调蓄设施排水效率较高，在保障极端降雨事件安全性方面具有重要作用，而绿色LID设施在径流污染控制、减少径流量、雨水资源综合利用等方面效果良好，二者有机结合有助于增强雨水系统的可靠性[3-4]。

灰色和绿色基础设施投资成本大，雨洪模拟系统复杂，控制参数量大面广，商业软件对参数调控的灵活性难以把握，计算结果的可解释性不强。因此，基于大数据经验研究灰绿耦合措施雨洪模型的优化算法，全面掌控方案迭代过程，并对最终结果进行综合评估，具有重要价值。前人研究主要集中在灰色和绿色基础设施布设位置、规模及组合等方面[5-8]，对二者耦合方式也进行了有益的探索[9-10]，但在排水系统建模基础上进行灰绿基础设施优化配置，并通过综合评价确定最优方案的研究较少[11-12]。本文以中山市某开发区为例，综合考虑经济性、区域径流控制能力和内涝风险性，量化评估灰色调蓄设施和绿色LID设施经济效益变化规律[13]，研究灰色调蓄设施和绿色LID设施规模优化方法，并对最终方案进行综合评估。

1 灰绿耦合雨洪模型的建立

1.1 研究区用地类型

中山市某开发区占地面积59.36 km2，地势西南高、东北低，地势平坦开阔，河网交织，排水体制为分流制。根据遥感卫星图像对用地类型进行划分(图1)。该区严重内涝点多发生在地势低洼区及排水管网未覆盖或者设计标准偏低的区域，假设雨水管网系统一定，可优化调控的灰色调蓄设施为调蓄池位置及容积，绿色LID设施特指常用LID措施。

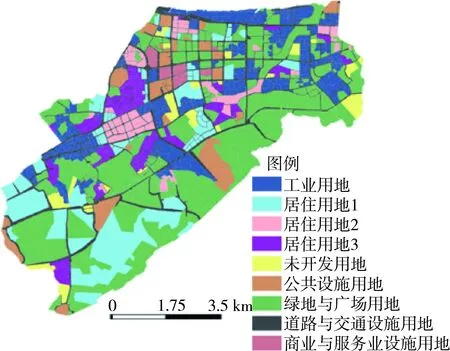
图1 研究区用地类型Fig.1 Land use type of study area

1.2 现状条件建模及模型率定

根据区域现状雨水管网设计图、用地类型图、DEM高程数据等资料及地勘校正，采用SWMM建模，研究区概化图见图2。概化模型包括1 706个检查井节点、466个排水口节点、1 701根雨水管网，雨水就近排入河涌，采用泰森多边形法划分子汇水区，进一步与用地类型以及规划汇水区图层叠加，明确各子汇水区排水节点。

采用中山市暴雨强度公式(式(1))，设计暴雨雨型采用芝加哥雨型，雨峰系数0.35。根据典型降雨条件分析需求，利用该地区现状条件下，年径流控制率为80%对应降雨(P≈0.06 a设计降雨)、P=3 a设计降雨及P=20 a设计降雨分别反映小雨、中雨、大雨3种典型的降雨边界条件建模，并由此构建SWMM模型。

图2 研究区概化示意图Fig.2 Schematic map of study area

(1)

式中：i为暴雨强度；P为重现期；t为降雨历时。

采用综合径流系数法[14]率定模型中不可测参数，结合地勘内涝位置综合评估参数设置合理性。该区域属建筑较密集区域，综合径流系数范围为 0.5～0.7[15]；根据实测数据，将P=1 a设计暴雨作为率定工况，在2 h设计暴雨条件下，模拟径流系数取0.69；下渗模型选择Horton模型，最大入渗速率为45 mm/h，最小入渗速率为2.5 mm/h，衰减系数为4 h-1；透水与不透水区域洼地蓄水量分别为5 mm、3 mm，粗糙系数n分别为0.015、0.25；管道粗糙系数为0.015；西南区地面坡度设为5%，其余设为8‰；子汇水区宽度为面积开方[16]。图3为模拟与实测内涝点对比，可见实测内涝点共计11个，模拟内涝区域共计13处，模拟及实测内涝点分布基本吻合，可认为模型参数设置合理。

图3 模拟及实测内涝点对比Fig.3 Comparison of simulated and measured waterlogging points

1.3 灰色调蓄设施及绿色LID设施初选

研究区暴雨频繁，下垫面地下水位高，黏土渗透性差，灰绿基础设施应以调蓄错峰缓排作用为主，并在现状模型基础上添加。灰色调蓄设施的形式主要包括但不限于调蓄池，还可以是多功能的深隧或行洪通道等，模型计算的目的是得到调蓄类设施的位置和容积，布设时应综合考虑内涝点位置可行性及空间合理性等因素。结合现状内涝情况分析，共布设11处调蓄池(图4)。与之配合的绿色LID设施主要根据用地类型及建设可行性确定，不同用地类型的LID组合初选结果及其最大布设比例见表1。

图4 灰色调蓄池布设分布Fig.4 Layout of storage ponds

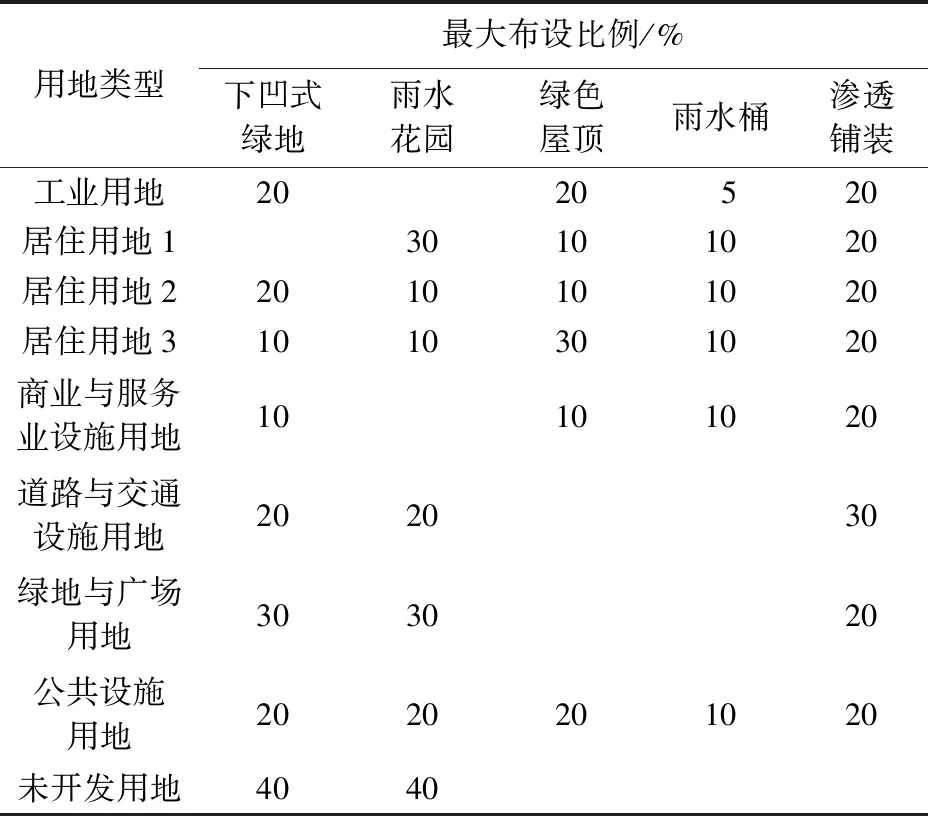
表1 不同用地类型的绿色LID设施及最大布设比例Table 1 Combination scheme and maximum layout proportion of green LID facilities of different land types

2 多目标优化模型

在前述现状雨洪模型及灰绿基础设施初选结果基础上构建多目标优化模型。灰色调蓄设施和绿色LID设施的规模为非线性优化问题，维数高，易于陷入局部点，本文采用基于二元锦标赛法和精英选择策略的NSGA-II算法，其计算效率高、搜索范围广[17]。根据开发区规模，设置种群规模为60，最大进化代数为100，交叉概率为0.9，变异概率为0.1。采用C++编写优化算法，通过调用SWMM动态链接库实现自动迭代。以灰绿基础设施总成本、径流系数和节点总溢流量为目标函数，以调蓄池容积和LID设施面积为决策变量，以布设规模范围作为约束条件，不同内涝风险等级对应不同惩罚因子构建罚函数，由此构建多目标优化模型。

2.1 目标函数

a.成本目标。总成本E作为灰绿基础设施目标函数F1，E为绿色LID设施成本EG和灰色调蓄设施成本EY之和。采用单位面积成本法估算绿色LID设施成本：

(2)

式中：Cij为第i个子汇水区第j种绿色LID设施的单价，元/m2；Aij为第i个子汇水区第j种绿色LID设施的布设面积，m2；Nm为第i个子汇水区应用的绿色LID设施种类数量；NL为研究区域子汇水区总数量。LID设施单价参考《海绵城市建设指南》并结合当地经济发展水平及工程实践确定，雨水花园、下凹式绿地、绿色屋顶、渗透铺装、雨水桶单价分别为450元/m2、85元/m2、300元/m2、320元/m2、100元/m2[5]。灰色调蓄池成本参考文献[18]估算：

(3)

式中：NS为研究区域布设的调蓄设施总数量；Vi为第i个调蓄设施的容积，m3。

b.径流控制目标。将径流总量R与降雨总量RI的比值，即径流系数φ，作为径流控制目标F2。

c.内涝控制目标。积水点溢流总量与渗透及调蓄设施、管网转输及泵闸排放、地下水位或河流水位等多因素相关，反映内涝程度，因此将其作为内涝风险目标函数F3：

(4)

式中：Q为节点溢流总量，m3；Qi为第i个节点的溢流量，m3；NJ为研究区节点总数量。

2.2 决策变量

在确定灰色调蓄设施布设位置、绿色LID设施适建比例的基础上对二者规模进行优化。灰色调蓄设施决策变量为各个调蓄池容积Vi；绿色LID设施决策变量为各个子汇水区LID布设面积Aij。

2.3 约束条件

为保证决策变量范围设置的合理性，加快优化过程的收敛，分别对灰色调蓄设施和绿色LID设施规模添加如下约束：

a.绿色LID设施约束条件：

(5)

式中：Ai为第i个子汇水区面积，m2；Aijmin为第i个子汇水区第j种绿色LID设施最小布设面积，m2；PCTij为第i个子汇水区的第j种绿色LID设施最大布设比例。

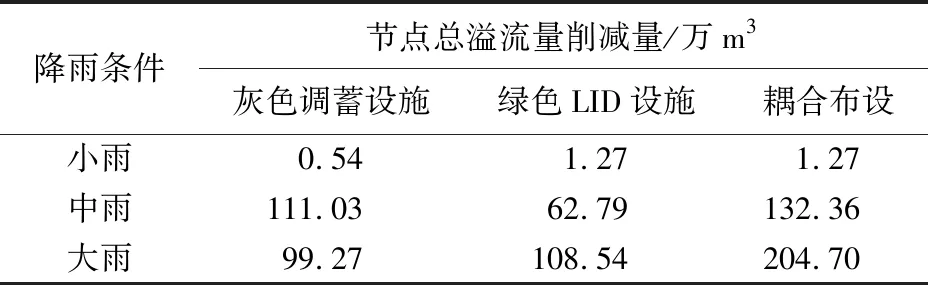
b.灰色调蓄设施约束条件：在现状模型中，将最大降雨重现期降雨作为输入条件，根据模拟所得各调蓄池最大容积确定调蓄池容积上限，即0

2.4 罚函数

为限制高风险个体的出现，以人员密度区分地区重要性，结合积水时间和深度划分内涝风险等级。人员密集及稀疏区域内涝风险等级划分标准见表2[19]。内涝风险等级D与惩罚因子M设置关系如下：D=0、M=1为无风险，D=1、M=1.2为低风险，D=2、M=1.5为中风险，D=3、M=2为高风险。内涝风险等级越高，惩罚因子越大，对应目标函数越大，从而可降低该个体进入下一代的概率。

表2 内涝风险等级划分标准Table 2 Classification standard of waterlogging risk grade

综上，多目标优化模型可表示为

(7)

3 结果与分析

基于多目标优化模型，降雨边界条件采用80%年径流总量控制率对应降雨(P≈0.06 a)、P=3 a、P=20 a的24 h设计暴雨分别反映小雨、中雨、大雨3种典型降雨，首先研究灰色调蓄设施及绿色LID设施效能与经济效益的相关性，其次对二者规模进行多目标优化，最后综合评价迭代过程，并选择最具经济效益的灰绿耦合设施实施方案。

3.1 灰绿基础设施经济效益分析

a.绿色LID设施经济效益分析。各子汇水区中不同绿色LID设施以步长Sij递增至最大布设面积，同时计算相应规模所产生的效益，步长公式为

(8)

式中：Aijmax为第i个子汇水区第j种绿色LID设施最大布设面积，m2；n为Aij由Aijmin增长至Aijmax的次数，本文取100。

小雨、中雨、大雨3种典型降雨条件下，绿色LID设施成本EG与节点总溢流量Q、径流系数φ关系如图5所示。可见，3种降雨条件下，EG-Q曲线最大切线斜率分别为0.008 4、0.85和1.5，EG-φ曲线最大切线斜率分别为0.002 2、0.003 0和0.003 2，均近似为直线，可据此估算投资成本产生效益或者根据规划设计目标估算投资成本。根据曲线最大切线斜率可计算单位成本绿色LID设施产生降雨重现期提升的边际效益。

b.灰色调蓄设施经济效益分析。与绿色LID设施类似，在现状雨洪模型的基础上添加灰色调蓄设施，每个调蓄池容积以步长1 000 m3从0开始增长至50万m3，并计算相应效益。3种降雨条件下，调蓄设施容积V与成本EY、节点总溢流量Q关系如图6所示。可见，V与EY接近线性关系，因此V-Q曲线趋势可反映EY-Q曲线趋势。V-Q曲线存在明显的拐点，拐点后规模/成本的增加并未产生额外效益，即降低节点中溢流量的边际效益趋0。因此设计方案中调蓄池总容积应小于拐点对应容积VT。

(a) 小雨

3种降雨条件下拐点处的容积VT、成本EYT、V-Q曲线拐点前最大切线斜率k1以及V-EY曲线拐点前最大切线斜率k2见表3，k1和k2代表了拐点前单位容积灰色调蓄设施所削减内涝水量和成本。根据拐点相关参数可评估调蓄池规模合理性，k1和k2均随重现期增加而增加，与绿色LID设施相比，相同降雨条件下，灰色调蓄设施单位成本节点总溢流量削减量远大于绿色LID设施。综合绿色LID设施经济效益分析结果，若需提升区域径流控制能力，绿色LID设施是必要的，但灰色调蓄设施更为经济，可根据灰色调蓄设施和绿色LID设施特点辅助设计方案决策。

表3 各降雨条件下曲线拐点处参数Table 3 Parameters at inflection point under different rainfall conditions

3.2 多目标优化结果

在前述建立的多目标优化模型基础上，对3种典型降雨条件下绿色LID设施和灰色调蓄设施规模同时进行优化。在预设的种群规模及最大进化代数下，各目标函数均可稳定收敛，说明NSGA-Ⅱ算法适用于灰绿基础设施规模多目标优化问题，表4列出了各目标函数收敛值及其与初代相比优化幅度。

不同降雨条件下达到稳定收敛时，灰绿基础设施单独布设的节点总溢流量削减量以及耦合布设节点总溢流量削减量对比见表5，可以发现，灰色调蓄设施和绿色LID设施单独布设产生效果小于耦合布设产生效果，灰绿设施耦合效果并非单独布设效果叠加，因此应将灰绿基础设施纳入同一模型模拟评估。

表4 不同降雨条件各目标函数收敛值Table 4 Convergence value of each objective function under different rainfall conditions

表5 不同降雨条件下布设灰绿基础设施节点总溢流量削减量Table 5 Reduction of total node overflow of gray-green infrastructure under different rainfall conditions

不同降雨条件下典型种群个体分布如图7所示，其中小雨条件下，所有节点无积水，节点总溢流量为0。由于种群个体变化，相较于初代，总成本、径流系数和节点总溢流量均呈现降低趋势，说明经过优化，降低成本的同时效益也得到提升，主要通过调整灰绿基础设施成本占比实现。图8为不同降雨条件下灰绿基础设施成本随遗传代数变化，可见小雨条件下，节点无积水，灰色调蓄设施成本由4.29亿元降至0.33亿元；中、大雨条件下，绿色LID设施成本呈现下降趋势，原因在于其径流和内涝控制效果下降，经济效益降低。小雨、中雨、大雨条件下，灰色调蓄设施成本收敛值分别为0.30亿元、2.8亿元、3.05亿元，灰色调蓄设施成本占比分别为1.6%、4.0%、4.5%，即降雨重现期越大，灰色调蓄设施成本占比越大，说明调蓄设施是解决内涝问题的有效手段。

3.3 优化方案集的综合评价优选

根据多目标优化可得到典型降雨条件下的优化方案集，进而对该解集中的方案进行综合评价，以获取最优实施方案。本文以灰绿基础设施总成本、径流系数和节点总溢流量为评价指标，优化解集个体数为60，采用客观赋权法中的熵权法进行赋权，由于评价指标数及个体数均较少，为充分利用原始信息，进一步采用TOPSIS法对各方案进行综合评价。

以第100代种群作为评价群体，3种降雨条件下，各指标权重及综合评价所得最优个体目标函数值见表6。可见，降雨由小至大，最大权重指标分别为径流系数、灰绿基础设施总成本以及节点总溢流量，根据权重分析结果，实际工程中，若以控制出现频次较多的小降雨工况为主要目标，建议更多采用绿色LID设施，而若以保障极端降雨安全性为目标，则建议结合灰色调蓄设施。此外，建议在中雨条件下对灰绿耦合排水系统进行优化，避免降雨过小或过大时，某种措施失效从而导致优化结果偏离实际，或者应当综合考虑多种降雨工况进行方案优选。最终优化方案取得效能为：小雨条件下，径流系数降低0.32，节点总溢流量减少1.27万m3；中雨条件下，径流系数降低0.23，节点总溢流量减少123.21万m3；大雨条件下，径流系数降低0.25，节点总溢流量减少209.923万m3，说明灰绿基础设施对于防洪排涝具有重要意义。