一种基于Jeffrey散度的鲁棒图像分割方法
单晓英,任迎春
(嘉兴学院:a.平湖师范学院;b.数据科学学院,浙江嘉兴 314000)
图像分割是计算机视觉领域的一个重要研究方向,其目的是将图像中感兴趣的部分准确地分割出来,为后续的图像分析提供依据.由于成像设备不完善和外界干扰,真实图像中经常出现灰度不均现象.灰度不均的图像,其待分割区域的灰度存在重叠范围,给图像分割带来挑战.
近年来,人们提出了很多图像分割方法,其中主动轮廓模型(Active Contour Models,简称ACMs)根据最小化能量泛函得到的偏微分方程来指导曲线的演化,可以获得高精度的闭合分割曲线,该类方法一直受到国内外学者的广泛关注.[1-3]ACMs可以分为基于边界的分割模型[4-5]和基于区域的分割模型.[6-9]前者利用图像梯度信息构造边界停止函数推动曲线演化并最终得到目标区域的轮廓线,代表性算法有测地线模型(Geodesic Active Contour,简称GAC)[10]、距离正则化水平集演化模型(Distance Regularized Level Set Evolution,简称DRLSE)[11]等.因为充分利用了目标区域内外的梯度信息,基于边界信息的主动轮廓模型对于边界清晰的图像分割质量较好,但在分割弱边界图像时质量较差.后者利用区域的灰度统计信息指导曲线向目标轮廓逼近,在分割弱边界或灰度不均图像时可以取得较好的效果.例如,局部图像拟合模型(Local Image Fitting,简称LIF)根据局部区域在演化曲线的内外高斯加权平均灰度函数可拟合图像灰度.[12]采用K-均值理论并最小化输入图像和每个像素点附近的局部聚类中心之间的差异,可得到一种局部灰度聚类模型(Local Intensity Clustering,简称LIC).[13]在LIC模型基础上,用一组给定的光滑正交基函数的线性组合估计偏置场,可得到局部不均灰度聚类模型(Local Inhomogeneous Intensity Clustering,简称LINC),进一步提高了模型的分割精度.[14]通过构造局部拟合图像及其平方拟合图像的混合区域能量泛函(Hybrid Region Image Fitting Energy Functional,简称HRIF),使灰度不均图像分割和偏置场校正可以同时进行.[15]上述基于区域的分割模型能有效分割灰度不均图像,但对演化曲线的初始位置和形状较敏感.另外,许多现有主动轮廓模型利用欧氏距离定义其外部能量约束项并通过该约束项度量分割图像与原始图像之间的差异,最终根据类内方差最小准则分割图像.如果图像存在灰度突变或噪声,会导致该区域灰度值方差变大,方差的不稳定会造成计算距离值的不稳定,从而导致分割结果的不稳定.Jeffrey散度是对称的KL散度,受方差不稳定性影响较小,[16-17]在模式识别和计算机视觉中被广泛应用.[18-20]
针对以上问题,本文提出一种新的图像分割方法.首先,根据Jeffrey散度构建图像拟合项以提升算法的灰度不均分割能力;其次,整合灰度拟合项及长度正则项、符号距离函数惩罚项得到总能量泛函,并通过最小化能量泛函同时实现偏置场修正和图像分割.为提高关于初始位置的鲁棒性和分割效率,本文提出一种新的偏置场初始化方法,在一些医学图像、合成图像和自然图像上的实验表明,与现有ACMs算法相比,本文所提模型不仅对初始轮廓具有较好的鲁棒性,而且还具有更高的分割精度和分割效率.
1 相关工作
1.1 LIC模型
为实现灰度不均图像分割,局部灰度聚类模型LIC将图像建模为
u(x) =B(x)J(x)+N(x)
(1)
其中J(x)是真实图像,B(x)为变化平缓的偏置场,N是加性噪声.在每个像素y的局部区域Oy内应用K-means聚类算法,[21]可以得到LIC模型的局部能量泛函:

(2)

(3)
给出,在两相分割即只将图像分为背景和目标两个不相交区域情形下,式(3)可改写为:
(4)
其中ν和μ为正的常值系数,Mi(φ)为Ωi的隶属函数且有M1(φ)=H(φ)和M2(φ)=1-H(φ),H(x)为Heaviside函数,[22]L(φ)为符号距离函数惩罚项,R(φ)为长度正则项函数.偏置场B(x)和演化曲线内外区域的灰度均值c1、c2可由
(5)
(6)
(7)
求出.由于建模时融入了偏置场和灰度信息,LIC具有同时进行图像分割和偏置场校正的能力.然而,该模型对初始化轮廓位置非常敏感,容易陷入局部最优.
1.2 LINC模型
在LIC模型基础上提出的局部不均灰度聚类模型LINC,其能量泛函为:
(8)
其中g(y)为15个四阶正交勒让德多项式函数,wT为相应多项式函数的系数.LINC模型具有一定的处理灰度不均图片的能力,但其处理强灰度不均图片的能力较差,而且关于演化曲线的初始位置较敏感.
1.3 HRIF模型
为解决分割灰度不均图像时遇到的边界泄漏和分割不充分问题,文献[15]提出了一种基于混合区域图像拟合模型HRIF,其能量函数为:
(9)
其中I(x)表示原始图像,IEFI(x)表示原始图像的拟合图像,ISFI(x)表示原始图像平方I2(x)的拟合图像,P(φ)和L(φ)分别为长度正则项和符号距离函数惩罚项,μ和ν为对应权重.
HRIF模型在分割灰度不均图像时还可以进行偏置场修正,一定程度上解决了弱边界泄露问题,但该算法对初始轮廓曲线的鲁棒性较差.
2 引入Jeffrey散度的鲁棒图像分割方法
2.1 基于Jeffrey散度的相似性度量
在度量图像相似性时,传统的方法是基于欧氏距离或Kullback-Leibler(KL)散度定义外部能量约束项并通过最小化原图像与分割得到的图像的类内方差寻求最优划分.如果遇到图像局部灰度变化强烈或存在噪声,会造成该区域灰度值方差变大,而方差在主动轮廓模型能量泛函构建时具有重要地位,方差的不稳定会影响图像分割的质量.Jeffrey散度是KL散度的改进版本,数值稳定性较好,在图像检索、图像配准和图像分割领域中被广泛应用.[19,23-24]
假定S=[s1,s2,…,sn]和V=[v1,v2,…,vn]为两个向量(或矩阵),n为相应的维度,基于Jeffrey散度的距离计算公式如下:
(10)
当S和V对应维度的数值越接近时,其差异性就越小;当它们各维度上的数值完全相等时,其距离为0;另外,Jeffrey散度本身具有对称的性质,可以直接作为距离使用.
2.2 基于Jeffrey散度的图像灰度拟合项
如文献[22-24]所述,当图像存在严重灰度不均现象时,利用欧氏距离计算演化曲线内外区域像素灰度的差异可能导致错误的分割结果.基于此,本文引入Jeffrey散度来衡量分割前后两图像区域间的灰度差异,图像拟合项定义如下:
EJIFT(φ,B,c1,c2)=
(11)
其中c1和c2分别是曲线演化过程中图像在inside(T)和outside(T)的灰度均值.
基于Jeffrey散度的图像拟合项可以提高模型处理灰度不均图像的能力,同时还可以进行偏置场修正.
2.3 总能量泛函

E(φ,B,c1,c2)=λEJIFT(φ,B,c1,c2)+μR(φ)+νL(φ)=
μR(φ)+νL(φ)
(12)
其中,λ、ν和μ为正的常值系数.
根据变分原理和最速下降法,可以得到式(12)的演化方程为
(13)
其中∇为梯度算子,div(·)为散度算子.
2.4 偏置场初始化策略
由于图像灰度变化趋势与偏置场变化趋势是一致的.在能量泛函最小化过程中,偏置场估计和图像分割相辅相成、互相影响.合适的偏置场初始化方法可以提升模型的分割精度和分割效率.因此,将偏置场初始化为:
(14)
其中Ωx为以x为中心、r为半径的局部圆形区域,n为Ωx中像素点的个数,m为给定图像u(x)的均值.由式(1)、式(14),可得:
(15)
一般来说,目标边界位于图像灰度变化较剧烈的区域.校正后的图像J0在目标边界附近的灰度会大于或小于m,而其他区域的灰度约等于m.因此,新的偏置场初始化方法可以确保偏置场的变化趋势与整体图像灰度的变化趋势是一致的.
综上,本文所提分割模型的实施步骤如下:
步骤1:初始化水平集函数φ;
步骤2:根据式(14)初始化偏置场B;
步骤3:根据式(6)、式(7)分别计算c1和c2;
步骤4:根据式(13)更新水平集φ;
步骤5:根据式(5)计算B;
步骤6:判断φ是否收敛,若不收敛则返回步骤3.
3 实验及结果讨论
本文的实验环境为Intel(R) Core(TM) i7-8565U,CPU@1.80GHz,RAM 16.00GB,Windows10操作系统,实现算法的工具为MATLAB 2011b.除另有说明外,在所有实验中均使用以下参数:高斯函数的标准差σ=3,ε=1,Δt=0.1,ν=1,λ=100,μ=0.002×255×255以及局部圆形区域Ωx的半径r设置为20.
3.1 灰度不均图像分割实验
图1展示了本文所提模型的分割过程.两幅图像呈现了明显的灰度不均.实验结果表明,本文所提模型能够快速且准确地定位到目标边界,具有很高的演化效率.

注:第1列为原始图像及白色初始化轮廓,第2列为经过1次迭代后的分割结果,第3列为本文模型的最终分割结果
图2分别展示了原始图像、本文所提模型的偏置场初始值、分割结果以及偏置场的最终估计值.从图2的结果可以看出,本文最终估计出的偏置场和偏置场的初始值与原始图像的整体灰度变化趋势相似,这与前文中关于偏置场的分析是一致的.图2的分割结果进一步证明了本文所设计的偏置场初始化方法的合理性和有效性.

注:从左至右图像分别为原始图像、初始化偏置场、分割结果和模型最终计算出的偏置场
3.2 初始轮廓鲁棒性实验
图3给出了本文模型对两幅灰度不均图像在不同初始轮廓下的分割结果.

注:黑色曲线表示初始化轮廓,白色曲线表示相应分割结果
图4给出了本文所提模型对两幅噪声图像在不同初始化轮廓下的分割结果.

注:第一行和第三行的白色曲线表示初始化轮廓,第二行和第四行的白色曲线表示相应分割结果
从图3和图4的实验结果可以看出,在各种不同初始化曲线下,本文模型均能成功分割出目标.这是因为本文模型融合了偏置场校正和图像分割,使两者相辅相成,确保图像灰度变化趋势与偏置场变化趋势的一致性.另外,由于本文所提的偏置场初始化方法模型(14)对各像素的局部邻域做了均值化处理,这在一定程度上消除了噪声带来的影响.
图3和图4的实验结果表明,无论是灰度不均图像还是噪声图像,本文模型对初始化曲线均具有较好的鲁棒性.
3.3 噪声图像分割实验
图5为本文所提模型在不同程度噪声污染情况下的3幅自然图像上的分割结果.从图5的分割结果可以看出,本文所提模型可以分割一定程度的噪声污染图像.

注:第1列为原始图像,第2列至第5列依次为添加speckle噪声(均值为0,方差为0.005)、speckle噪声(均值为0,方差为0.03)、Gaussian噪声(均值为0,方差为0.005)、Gaussian噪声(均值为0,方差为0.03)的分割结果
3.4 分割效率及分割精度比较
本节将从分割效率和分割精度两个方面展示本文所提模型的优越性能.分割效率包括完成分割的迭代次数和计算时间,分割精度包括骰子系数(Dice Similarity Coefficient,简称DSC)和Jaccard相似度(Jaccard Similarity,简称JS)两个常用评估指标,定义如下:
(16)
其中,B为参考的分割标准,A为测试模型的分割结果,N(·)表示某一区域的像素数目,∪和∩表示两区域的并或交算子.DSC和JS值在0到1之间,它们的数值越接近1,表明算法的分割质量越高.
图6为本文所提模型与LIC、LINC和 HRIF分别在两幅灰度不均合成图像(A和B)、两幅医学图像(C和D)和两幅自然图像(E和F)上的分割结果.
从图6可以看出,对于第1行和第2行的灰度不均图像,本文模型和 HRIF均能分割出理想结果,而LINC和LIC提取目标边界的能力不足,尤其是LINC在给出的两幅灰度不均图像均分割失败.对于第3行和第4行的血管图像,本文所提模型和LINC分割质量比LIC和 HRIF的分割质量要高.对于第5行和第6行的自然图像,本文所提模型分割结果优于LIC、 HRIF和LINC模型.
从图6的分割结果可知,本文所提模型在针对灰度不均图像、医学图像及自然图像时均具有较好的分割性能,这是因为本文模型利用Jeffrey散度构建图像灰度拟合项,相比其他三种模型,具有更强的目标边界提取能力.
表1和表2分别列出了4种模型分割6幅图像时的迭代次数和分割时间,用加粗显示的数据是用时最短的迭代次数和分割时间,用斜体加粗显示的数据是用时最长的迭代次数和时间.从表1和表2的实验结果可以看出,本文所提模型迭代次数最少,执行分割的时间也最短.这是因为本文模型设计的偏置场初始化方法更加有效,可以加速算法的收敛过程.
表3和表4分别列出了4种模型分割6幅图像时的JS值和DSC值,最大的JS值和DSC值用加粗字体标出,最小的JS值和DSC值用斜体加粗标出,可以看出,本文模型在JS值和DSC值两个分割指标上均取得了最大值,这与图6的分割结果相一致.
总之,本文模型不仅具备较好的图像分割能力,具有较高的分割效率.

注:图像A和图像B为合成图像,图像C和图像D为医学图像,图像E和图像F为自然图像.从左到右:第1列为原始图像,第2列至第5列依次为本文模型、LIC模型、LINC模型和 HRIF模型的分割结果
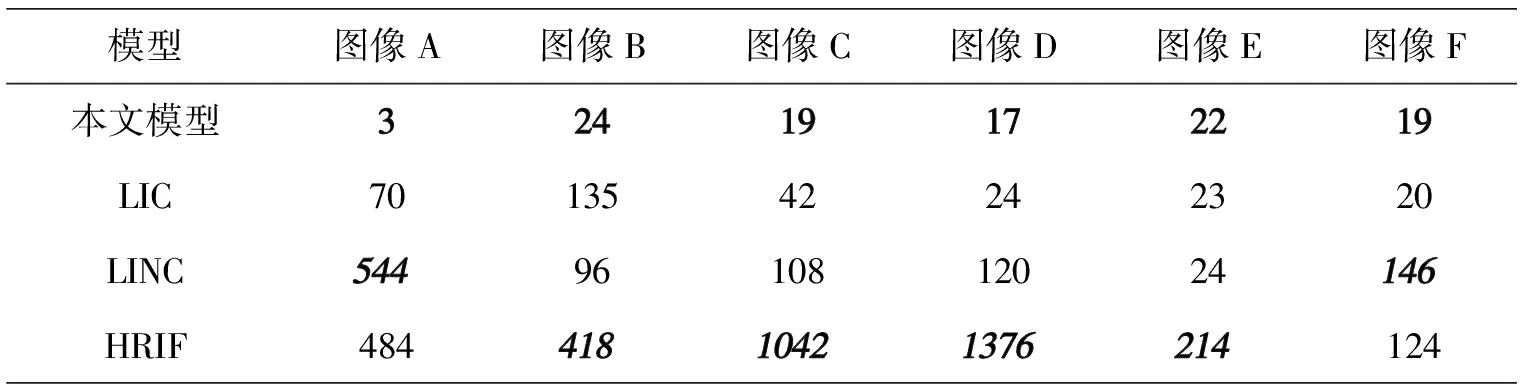
表1 本文模型与LIC、LINC和 HRIF在分割图6的6幅图像之迭代次数比较
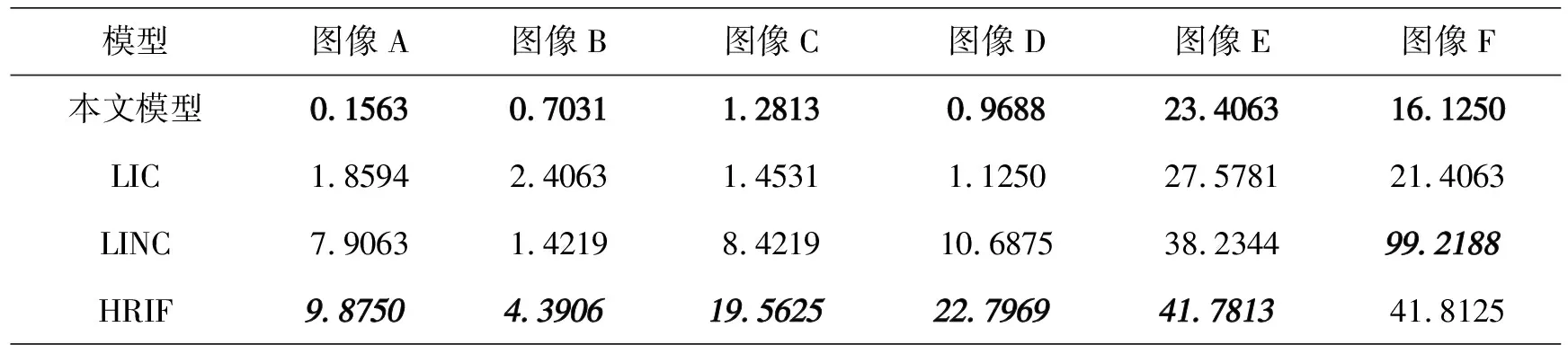
表2 本文模型与LIC、LINC和 HRIF在分割图6的6幅图像时之时间比较 s

表3 本文模型与LIC、LINC和 HRIF分割图6的6幅图像之JS系数比较

表4 本文模型与LIC、LINC和 HRIF分割图6的6幅图像之DSC系数比较
4 结论
针对现有基于区域的主动轮廓模型分割灰度不均图像时初始位置鲁棒性较差的问题,本文提出一种基于Jeffrey散度相似性度量的图像分割算法,建立了基于Jeffrey散度的灰度拟合项,整合了长度正则项、符号距离函数惩罚项和灰度拟合项构建总能量泛函,并通过最小化能量泛函实现了偏置场修正和灰度不均图像分割,引入了一种新的偏置场初始化方法以提高算法的分割效率和初始轮廓曲线的鲁棒性.实验结果表明,本文模型不仅对初始轮廓曲线具有较好的鲁棒性,而且具有更高的分割精度和分割效率.

