一类交错扩散型Lotka-Volterra竞争系统的全局稳定性

汪建俏

(浙江师范大学 数学与计算机科学学院,浙江金华321004)

在过去的几十年里,反应扩散方程被频繁地作为基本模型解决与空间生态和进化相关的问题，其中最重要的例子是两物种的Lotka-Volterra竞争-扩散系统.[1-8]近来，资源空间分布不均匀所带来的空间异质现象对两物种的Lotka-Volterra竞争-扩散系统产生了较大的影响,当平流项被纳入这些经典的Lotka-Volterra竞争-扩散系统时,所产生的反应-扩散-平流系统的全局动力学还远远没有被完全理解,因此，这一系列问题引起了许多生物学者和数学学者的关注.

1 相关研究与假设

本文聚焦在非均匀环境中的Lotka-Volterra反应-扩散-平流系统下的两个物种扩散的动力学行为:

(1)

首先，做如下假设：

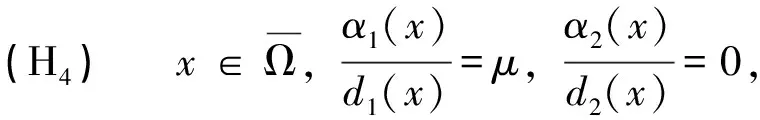
其中∇是梯度算子.u、v分别代表两物种在位置为x、时间为t的情况下的种群密度,mi(x)∈C2(Ω)表示非均匀资源的密度,∇m表示考虑沿资源梯度迁移的定向运动.∇·(∇)是求div(∇)，即意味着具有扩散现象.非负函数aij(x)∈C2(Ω)是两物种在位置为x处的强度.这里的扩散系数d1(x)、d2(x)和平流率α1(x)、α2(x)分别代表的是物种u、v在位置x处的随机扩散率和平流速率.扩散系数、平流系数、资源函数和竞争率都是空间异质的.集合Ω⊂N代表的是封闭环境同时有光滑的边界条件∂Ω.为边界∂Ω上的单位外法向量.齐次无通量边界条件表明,该系统是自包含的,且跨越边界的总体通量为0.其中，在生物学上，假设(H2)、(H3)、(H4)意味着两物种的平流率和扩散率之比是一个常数.

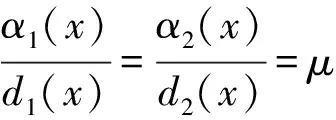
最近,文献[11]研究了空间扩散和资源空间变异对种群持久性和排斥性的综合影响,提出了扩散的Lotka-Volterra竞争模型

(2)

文献[11]在di、mi和aij是空间非齐次的情况下,用一种新的李雅普诺夫函数方法证明了模型(2)中非常数正平衡解的全局稳定性.

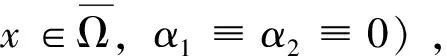
在上述工作的基础上,在第2节中,我们给出了一些预备知识.在第3节中,我们首先给出了一个标量空间异质扩散Logistic模型的非常数平衡解的全局稳定性(见定理1),其次分别考虑在条件(H1)、(H2)和条件 (H1)、(H3)下,系统(1)的正平衡解的全局稳定性(见定理2和定理3).

2 预备知识

首先，回顾一个关于二阶抛物方程一致估计的结果：

(3)

(h3) 对于特定的σ1<σ2,f∈L∞(Ω×[0,∞)×[σ1,σ2])且存在C(σ1,σ2)>0，使得

|f(x,t,u)-f(x,t,v)|≤C(σ1,σ2)|u-v|,∀(x,t)∈Ω×[0,+∞),u,v∈[σ1,σ2],

事实上，公式(3)的正有界解存在性可以通过文献[12]中的方法得到，对于公式(3)的全局定义的解u(x,t)，可以得到全局有界性的结果，这一点可以通过文献[13-14]中方法推导出来.

引理1令u(x,t)是系统(3)的一个解并且对于特定的σ1、σ2∈,σ10使得

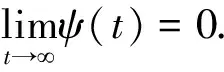
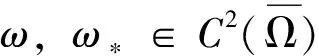
回顾标量演化方程如下：

(4)

(5)

的唯一正解，其中α>0.θd,α,m,a的存在和唯一性可以由文献[1]推导出来.

3 主要结果和证明

考虑式(4)的非恒定稳态的全局稳定性，也就是式(5)的解θd,α,m,a.

(6)

再利用李雅普诺夫函数，可以得到关于式(4)的解θd,α,m,a的全局稳定性.

证明由文献[1]可知方程(4)的解的存在唯一性，通过引理1可知，存在一个常数C>0，使得

(7)

为了简便，定义θd,α,m,a=θ.定义函数F:[0,∞)→如下:

(8)

那么，对于t≥0,F(t)≥0.F(t)再对t求导，结合方程(6)有:

(9)

结合引理3，简化J1和J2如下：

(10)

(11)

将式(10)、式(11)代入式(9)，得到

(12)

利用式(7)，在[1,∞)上对于某些C>0，有|φ′(t)|≤C.通过引理2，有

(13)

(14)

故

(15)

定理证毕.

注1：此定理的平流率和扩散率之比的负号表示该物种沿着与资源梯度迁移相反的方向运动.证明了拥有其能力的物种的解的全局稳定性.

(16)

根据文献[1,16-17]和极大值原理，式(16)是一个单调系统，系统(16)有唯一的共存解.

定理2 若假设(H1)和(H2)成立，则式(16)有一个正稳态解(u*(x),v*(x))且存在常数θ1>0,θ2>0使得

(17)

进一步假设

(18)

证明：利用引理2和引理3的结果进行证明.

假设式(18)成立.定义一个函数V：[0,∞)→，

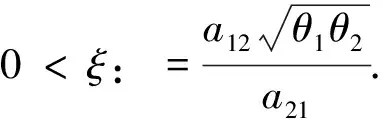
由式(16)，有如下结果

类似地，也能得到

那么，再由引理3，得到：

(19)

注意到式(17)和(18)，这意味着

(a12u*eμm+ηm+a21v*eμm+ηmξ)2-4ξu*v*a11a22e2μme2ηm<0.

由此可知，可选择合适的ε(0<ε≤1)使得

(a12u*eμm+ηm+a21v*ξeμm+ηm)2-4ξu*v*e2μme2ηm(a11-ε)(a22-ε)<0.

上式结合式(19)，可得到

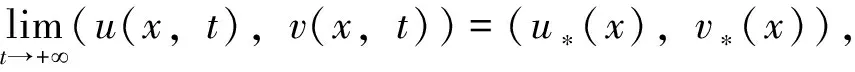
注2：定理2用了新的李雅普诺夫函数，证明了在一定的条件下，当平流率和扩散率之比都是正常数的时候，两个竞争物种的平衡解的全局稳定性.

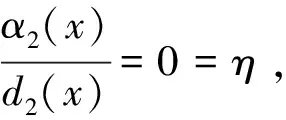
(20)

根据文献[1,16-17]和极大值原理，式(20)是一个单调系统，系统(20)有唯一的共存解.

其中(u,v)是式(20)的解，且式(20)在任意初始条件下有(u(x,0),v(x,0))满足u0(x),v0(x)≥0且u0(x),v0(x)≢0.

证明：与定理2的证明类似.定义函数W:[0,∞)→如下：

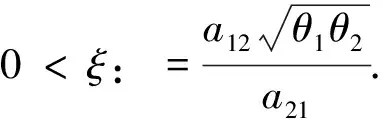
结合式(20)和引理3，有：

注意到式(17)和式(18)，则意味着

(a12u*eμm-ηm+ξa21v*eμm-ηm)2-4ξu*v*a11a22e2μme-2ηm<0.

由此可知，可选择合适的ε(0<ε≤1)，使得

(a12u*eμm-ηm+ξa21v*ξeμm-ηm)2-4ξu*v*e2μme-2ηm(a11-ε)(a22-ε)<0.

上式结合式(19)，可以得到

证毕.

注4定理3用了新的李雅普诺夫函数，证明了在一定的条件下，当平流率和扩散率之比一个为正常数、另一个为负常数(其中负号代表该物种有逃离有利于它的竞争者的环境的能力)的时候，两个竞争物种的平衡解的全局稳定性.

4 结语

在文献[10]中，两个竞争物种的平流率和扩散率之比是相同的常数，物种v没有逃离的能力，从而得到物种共存且平衡解的全局稳定性的结论.而本文与文献[10]的不同之处在于：当两个物种都生活在异质环境中，都有沿资源梯度迁移的速率，平流率和扩散率之比是不同的常数，其中物种u有沿着有利于自身的环境移动的能力，而物种v有逃离有利于它的竞争者的环境的能力.但在一定的条件下，物种u不能消灭物种v，物种v也不能消灭物种u，从而两者共存且得到了平衡解的全局稳定性的结果.