SIR疫苗免疫模型稳定性分析
王晶囡,甘畅鲲,夏晓峰,王宏宇,吴兴豪
(哈尔滨理工大学 1.理学院,2.电气与电子工程学院,黑龙江 哈尔滨 150080)
0 引言
传染病是由某些病原体通过人或动物之间接触相互传播的一类疾病,如触接传播流行性感冒、垂直传播的艾滋病和虫霉传播的疟疾等。(1)参见唐三一、肖燕妮:《生物数学》,北京:科学出版社,2019年,第89—100页。有些传染病,如新型冠状病毒肺炎(novel coronavirus pneumonia, NCP) 简称新冠肺炎,具有近距离传染力强、人群普遍易感、聚集性发病现象。(2)参见陈恩富:《疫苗时代新型冠状病毒肺炎疫情防控策略》,《预防医学》 2021年第3期。人们根据疾病的发生和传播机理,用数学工具建立反应传染病特点的数学模型,通过对模型的动力学分析和数值模拟,揭示和预测疾病的发展规律,找到疾病流行的关键因素,从而来制定阻断传染病的有效措施。(3)参见马知恩、周义仓:《传染病动力学的数学建模与研究》,北京:科学出版社,2004年。早在1927年,科迈克(Kermack)与麦肯德里克(McKendrick)将总人口分为易感者、感染者和恢复者三类,建立了经典的SIR模型,刻画了感染者康复后可以产生终身免疫力的一类传染病。(4)参见Kermack WO, Mckendrick A G:“A Contribution to the Mathematical Theory of Epidemics, ” Proceedings of the Royal Society of London. Series A, Containing papers of a Mathematical and Physical Character, vol. 115, no 772 (Aug1927).随着科研的发展,人们对SIR模型进行了改进,将传染期间的出生和死亡考虑到SIR模型当中,如当传染病的染病时间较长时,在模型中增加了常数出生项、常值输入项、死亡项和治疗项等,并研究了分支等动力学问题。(5)参见Wang Jinling, Liu Shengqiang: “Qualitative and bifurcation analysis using an SIR model with a saturated treatment function,” Mathematical and Computer Modelling, Vol.55, no3-4 (Feb.2012).对SIR模型的研究,已取得了丰硕的研究成果,如当传染病暴发时,及时接种疫苗、进行传媒宣传和隔离等措施是最好阻断传染病发展的方式,为有效地控制病情的传播提供了理论支持,因而现代传染病的动力学研究也成为应用数学热门方向之一。(6)参见Manuel De Ia Sen, Asier I: “On a Sir Epidemic Model for the COVID-19 Pandemic and the Logistic Equation, ” Discrete Dynamics in Nature and Society, vol.2020 (Dec.2020).
本文将以传播动力学SIR模型为基础,建立SIR疫苗免疫染病动力学模型。通过分析SIR疫苗免疫模型平衡点的稳定性,找到判断传染病是否可以流行传播的阈值,即模型的基本再生数,从而分析和预测疫苗免疫接种的比率和接触率的大小对传染病防控的影响。(7)参见高旭、王晶囡:《含有免疫作用的SIR传染病模型的动力学性质分析》,《高师理科学科》2018年第2期。
1 SIR疫苗免疫模型及平衡点的存在性
将疫苗免疫引入到典型的SIR传染病模型当中,具体形式如下:
(1)
其中S(t),I(t),R(t)分别表示易感者,感染者和移出者的数量,ν(≥μ)为易感者的出生率,μ表示自然死亡率,β表示病毒的传染率,a表示疫苗接种率;γ表示治愈率,Ω={(S,I,R)︳S,I,R≥0,S+I+R≤M}为模型(1)的正不变集。
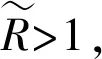
(2)
(3)
证明:平衡点处满足的方程如下:
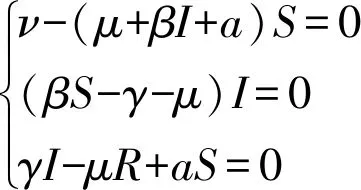
(4)
下面分I=0和I≠0这两种情况讨论。当I=0时,由方程(4)的第一个方程可得
(5)
再将I=0时与式(5)代入,可得
即得出无病平衡点P0(S0,0,R0)的具体表达为
当I≠0时,由方程(4)中的第二个式子可得
(6)
由方程(4)中的第一个式子可得
(7)
将式(6)和式(7)代入方程(4)中的第三个式子可得
2 平衡点的局部稳定性
证明:模型(1)在无病平衡点P0(S0,0,R0)的线性化系统的雅克比矩阵为
因而可得特征方程为
(8)
由(3)可知:

则平衡点P0处的特征方程的3个特征根均为负特征根,故P0为局部渐近稳定的。
模型(1)在平衡点P*(S*,I*,R*)的线性化系统的雅克比矩阵为
因而可得特征方程为
(9)
由(9)可知
(10)
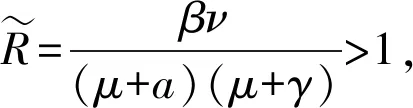
3 平衡点的全局稳定性
证明由于总人口数满足S(t)+I(t)+R(t)=N(t),将模型(1)中的三个方程相加得到
(10)
将方程(10)和模型(1)的前两个方程组成如下模型
(11)
下面应用李雅普诺夫函数方法证明模型(11)平衡点的全局渐近稳定性,再由模型(11)与模型(1)平衡点稳定性的等价性可推知模型(1)无病平衡点P0(S0,0,R0)与地方病平衡点P*(S*,I*,R*)的全局渐近稳定性。

两边沿着方程(11)对时间求导可得
由ν-μN0,经化简可得
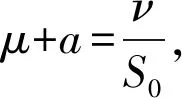
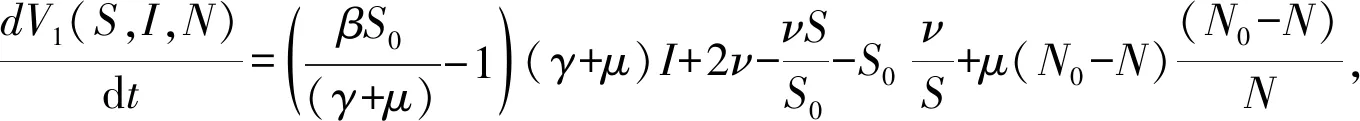
(12)


两边沿着方程(11)对时间求导可得
由βS*-γ+μ0和ν=μN*,经化简可得
再由(μ+a)S*=ν-βI*S*,经化简可得
再由βI*S*=I*(γ+μ),经化简可得
经化简可得
(13)

3 模型仿真分析
为验证定理1和定理2的理论结果,假设系数满足如下数值
ν=0.060,γ=0.00816,μ=0.000408。
(6)
根据定理1得到基本再生数随接种率和接触率的变化规律。如图1所示。

图1 接种率-接触率-基本再生数的关系式
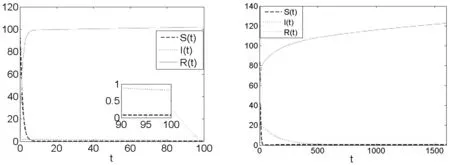
图2 当β=0.0048,γ=0.00816时,模型(1)的波形图
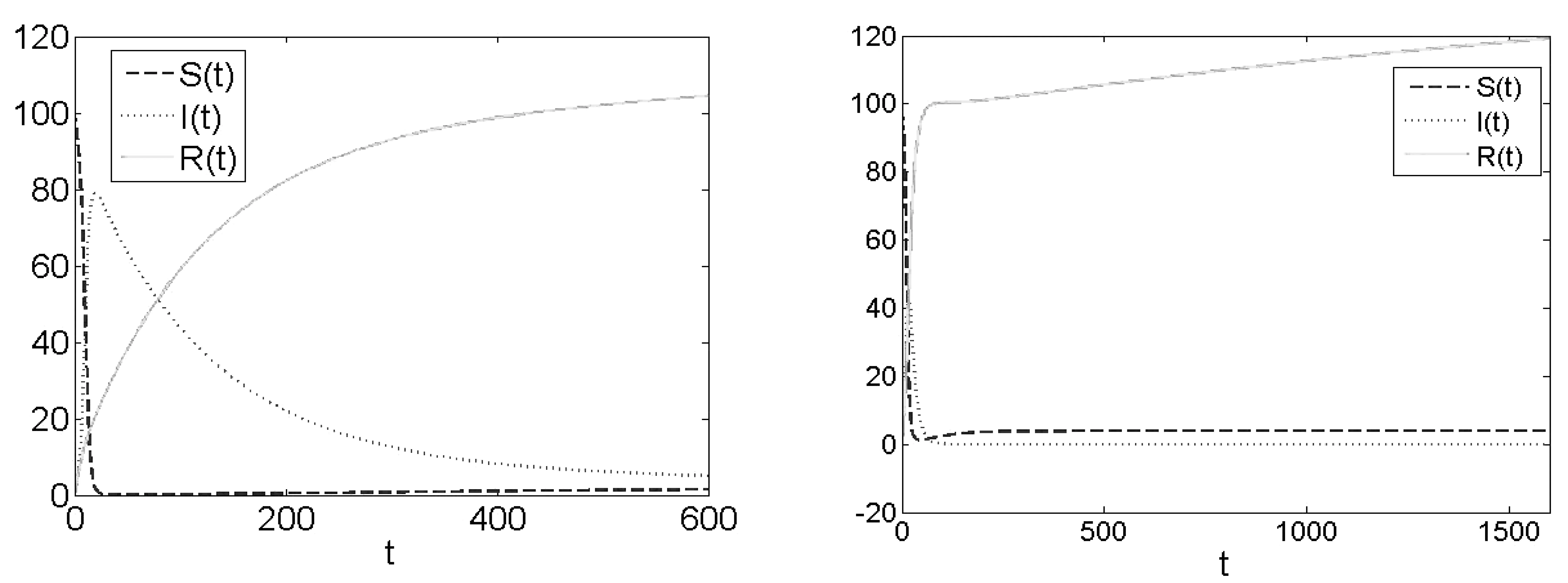
图3 当β=0.0048,a=0.015时,模型(1)的波形图
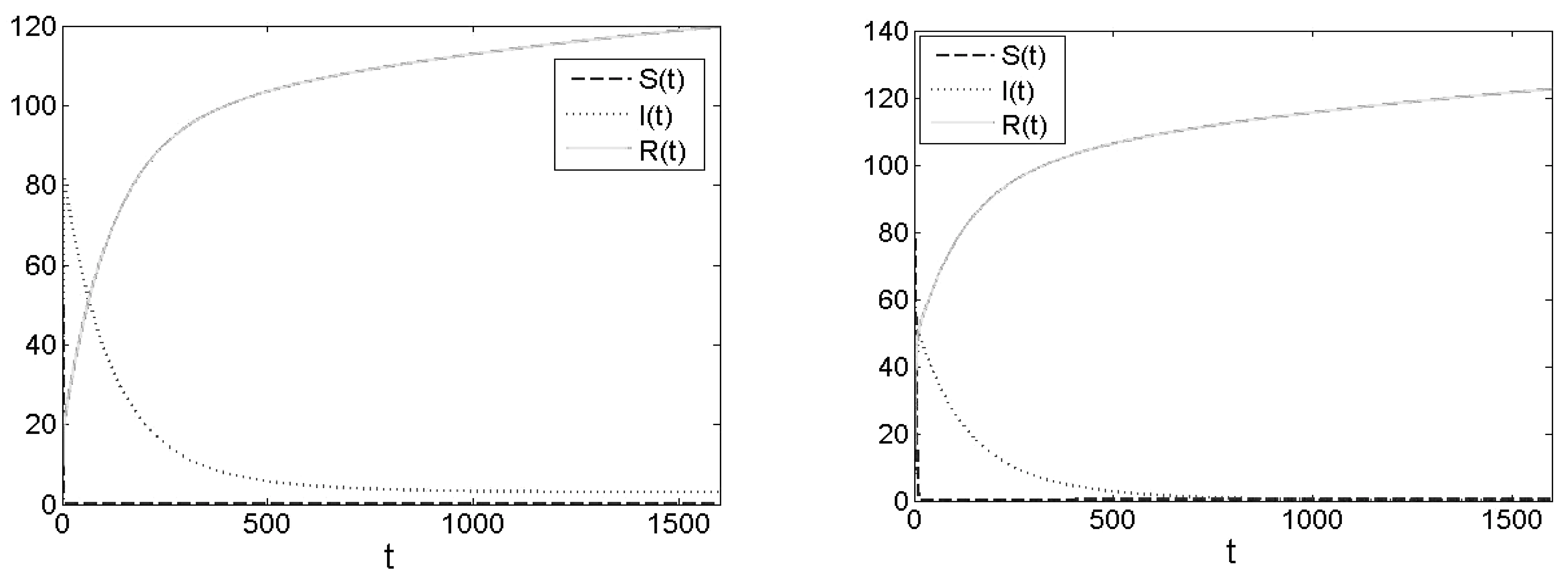
图4 当a=0.12,γ=0.00816时,模型(1)的波形图
4 结论
从理论推导结果与数值仿真结果可知,建立的SIR疫苗免疫模型,能基本预测传染病接种疫苗比率与传染病传播趋势之间的关系。因此,当有新冠疫情等传染病爆发时,研制并接种有效疫苗是非常必要的。同时也说明,建立免疫屏障的重要性。另外,还可以提高治愈率,提高医疗水平来增大治愈率,从而控制新冠疫情等传染病的传播。为了优化疫情防控,在增加接种率的同时,减少接触,降低接触率同样也很重要,是降低传染病传播风险的又一途径,所以疫情期间适当限制车辆出行,限制进出大超市人数,限制集体活动的举办,都是为了尽快控制疫情的发展,从而尽早恢复居民群众正常生产生活秩序,作为市民在各种传染疫情爆发时,应积极配合,疫情防控才能早日取得成效。

