双脉冲发动机Ⅰ脉冲工作过程中EPDM隔层烧蚀特性①

卞云龙，李映坤，李海阳，申志彬，吴国夫

(1.国防科技大学 空天科学学院，长沙 410073；2.中国航天科工集团有限公司六院四十一所，呼和浩特 010010；3.南京理工大学 机械工程学院，南京 210094)

0 引言

传统固体火箭发动机在能量管理和推力可控方面缺乏灵活性。因此，提出了一种双脉冲固体火箭发动机[1](简称双脉冲发动机)的概念。该发动机采用脉冲隔离装置将燃烧室分隔成两个部分，并共用一个喷管，可以进行两次点火。脉冲隔离装置作为双脉冲发动机核心部件之一，主要有非金属隔塞式、陶瓷舱盖式、金属膜片式、软质隔层式等多种类型，其中软质隔层式隔离装置具有装药密度大、结构简单、质量轻等特点[2]，一般由三元乙丙(EDPM)橡胶材料制成，该材料具有绝热性能好、热分解温度高、热分解吸热量大、密度低等优点。目前，已有多个国家将软质隔层式双脉冲发动机作为其导弹武器的动力系统，如美国标准-3导弹的第三级动力装置。

针对软质隔层式双脉冲固体火箭发动机，国内外学者相继展开了大量研究。国外STADLER等[3-4]设计了轴径混合隔层式双脉冲发动机，测得了两级脉冲工作时的压力、推力随时间变化曲线，并将其作为导弹的动力装置展开了两次飞行实验。KIM等[5]进行了脉冲点火时间间隔分别为2 s和60 s的隔层式双脉冲发动机地面静止实验，测得了Ⅰ脉冲工作过程中隔层内侧表面温度。国内曹熙炜[6]和王硕[7]等开展了含预制缺陷的软质隔层实验研究，通过数值仿真分析了隔层的破裂过程和应力分布及其影响因素；刘洪超等[8]采用ABAQUS有限元仿真软件分析了Ⅰ脉冲发动机工作过程中Ⅱ脉冲端燃药柱与隔层的变形情况，并通过快速增压冷气实验进行验证；王春光等[9-10]采用扩展有限元XFEM技术研究了脉冲隔离装置轴向隔层的破裂过程，提出了脉冲发动机中隔层传热炭化模型[11]。刘亚冰等[12]等发现，Ⅰ脉冲燃烧室燃气漩涡区位置的绝热层烧蚀较为严重；孙娜等[13]则指出，Ⅰ脉冲燃烧室内气流再附着点附近刚好为绝热层烧蚀较为剧烈的部位；陈雄等[14]基于耦合传热方法研究了隔层通道孔径对Ⅰ脉冲燃烧室热防护层的影响；惠博等[15]开展了Ⅰ脉冲绝热材料的二次烧蚀特性实验研究。杨春庆等[16]采用双向流固耦合仿真研究了轴向隔层式双脉冲发动机Ⅱ脉冲点火过程，分析了隔层的变形胀大特性以及燃气在发动机内的传播特性。付鹏等[17]采用显示动力学方法数值模拟了Ⅱ脉冲发动机工作中轴径混合式隔层反向打开过程。范兴贵等[18-20]建立了描述EPDM软隔层在有限变形下的率相关粘超弹本构模型。王坚[21]和李映坤[22]等采用双向流固耦合仿真研究了轴径混合双脉冲发动机Ⅱ脉冲点火过程中燃气流动过程和隔层变形胀大过程。然而，Ⅰ脉冲工作过程中软质隔层需经历较长时间高温燃气流的烧蚀作用，如果隔层厚度不足、质量不佳或强度不够，会导致二脉冲药柱和隔层系统结构完整性破坏，或者二脉冲药柱提前引燃，发动机燃烧室压强迅速攀升，导致发动机解体；相反，若隔层结构设计冗余，增加整个发动机的消极质量，严重影响发动机的工作性能。目前，尚未有双脉冲发动机隔层热环境和传热烧蚀仿真和实验研究的公开报道。

本文开展了双脉冲发动机Ⅰ脉冲工作中热环境仿真研究，建立了Ⅰ脉冲燃烧室两相流动仿真模型，分析了隔层工作过程的热载荷环境特性。在此基础上，提出了隔层烧蚀过程计算方法，开展隔层热解烧蚀过程仿真研究，获得隔层烧蚀量和内部温度的变化历程。最后进行Ⅰ脉冲发动机工作条件下的隔层烧蚀试验，对烧蚀仿真结果进行了验证，可为双脉冲发动机脉冲隔离装置隔层的研制提供理论基础与试验数据。

1 双脉冲发动机燃烧室热环境计算

1.1 物理模型与数值计算方法

双脉冲发动机Ⅰ脉冲工作过程中热环境仿真研究的基本假设包括：气相满足理想气体状态方程，不考虑气相化学反应；忽略颗粒相的燃烧、破碎、蒸发过程以及气固两相间能量的交换；不考虑固体推进剂燃面的退移，假设燃气流动为准稳态。燃气流动通过定常可压缩Navier-Stokes控制方程组来描述，湍流模型选择 SST两方程湍流模型，采用随机轨道模型追踪颗粒相的运动轨迹。本文利用FLUENT求解器进行稳态计算，空间离散采用AUSM和MUSCL格式。

轴径混合隔层式双脉冲发动机Ⅰ脉冲工作过程热环境计算物理模型与边界如图 1所示。图1中，Ⅰ脉冲药柱与Ⅱ脉冲隔层表面之间存在人工脱粘缝，该缝隙宽度为1.5 mm。为减小计算量，考虑结构的对称性，整个计算模型取1/9，计算域网格单元总数约为1 400 000，近壁面和隔层表面处网格进行局部加密处理，壁面第一层网格单元高度为1×10-5m，以确保近壁面处y+≤1.0。

(a)Physical model

1.2 气固两相边界条件设置

计算模型边界如图 1所示，Ⅰ脉冲药柱加质表面采用质量流率入口边界条件，燃气垂直于药柱表面注入燃烧室，质量流率为3.4 kg/s，燃气温度为3 500 K，加质表面流入颗粒为Al2O3，质量流率为气相的10%，颗粒粒径设置为70 μm[23]。计算模型喷管出口设置为压力出口边界，出口压强和温度分别设置为101 325 Pa和300 K。喷管出口处颗粒相设置为逃逸，即当颗粒抵达喷管出口随即停止对该颗粒的追踪计算。隔层外表面、燃烧室壁面、喷管壁面均设置为无滑移壁面边界条件。

1.3 燃烧室内热环境计算结果分析

双脉冲发动机Ⅰ脉冲工作时燃烧室内的温度分布和流线图如图 2所示。由图2可见，由于此时Ⅰ脉冲发动机处于稳定工作阶段，高温燃气充满整个发动机燃烧室，温度分布均匀；从流线图中可以发现，隔层与Ⅰ脉冲药柱前端形成了一个涡流区域，此处的强迫对流换热高于隔层的其他部位。双脉冲发动机Ⅰ脉冲工作时燃烧室内的颗粒运动轨迹如图 3所示。由图3可见，Ⅰ脉冲工作时，颗粒从药柱表面喷出流入Ⅰ脉冲燃烧室，随着燃气流动向下游运动，未进入燃烧室头部，部分颗粒在隔层轴向和径向过渡段停留时间较长。

(a)Temperature contour

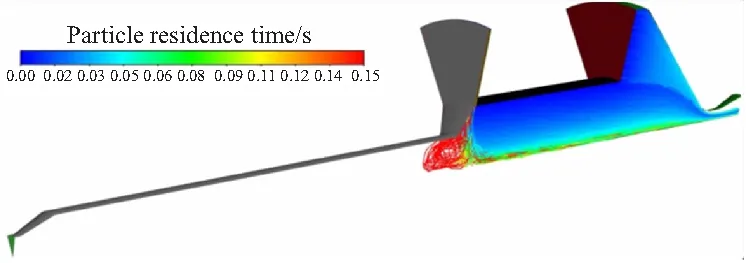
图3 燃烧室内颗粒运动轨迹图

图4所示为隔层表面的热流密度分布。可以看出，隔层前后根部位置处的热流密度均较小，Ⅰ脉冲工作时沿着隔层轴向表面热流密度逐渐升高，中部往后至隔层轴向与径向的过渡段，隔层表面的热流密度快速上升达到最大值，表面热流密度维持在5.0 MW/m2左右。随后，隔层表面热流密度沿着径向开始降低，最小值位于隔层根部。

图4 隔层表面热流密度分布

2 隔层烧蚀控制方程与计算方法

本文EPDM隔层材料的热防护模型采用热解层模型，即随着隔层表面的持续加热，隔层将出现分层，包括炭化层、热解层和原始层，如图 5所示。在Ⅰ脉冲燃烧室热流作用下，隔层表面逐渐升温，同时热量以热传导的形式向隔层内部传递，当温度达到材料热解温度后，隔层原始材料开始热解，热解产生的气体透过炭化层向外扩散，当温度达到炭化温度后，材料热解结束，同时形成了可渗透疏松多孔的炭化层结构。

图5 EPDM隔层烧蚀模型

2.1 隔层热传导控制方程

假设EPDM隔层材料的热导率为各向同性，基于傅里叶定律建立的隔层材料三维非稳态热传导控制方程为

(1)

式中U=ρcpT，其中ρ、cp、λ分别为隔层材料密度、比定压热容和热导率；Qtot为材料单位时间、单位体积内的总热量。

(2)

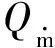
(3)

式中Hgas为热解气体显焓；ε为材料表面发射率；σ为斯忒藩·玻尔兹曼常数；Tref为外界环境参考温度；Hvir为绝热材料的热解潜热。

此外，本文热解气体、比热容和热导率的变热物性模型和EPDM材料相关参数见文献[24]。

2.2 热化学烧蚀模型

隔层烧蚀过程中表面发生热化学反应，隔层表面的碳原子作为反应物与燃气中的CO2和H2O气体反应，该过程消耗碳的质量流率为

(4)

(5)

式中pC,H2O和pC,CO2分别为H2O和CO2的分压;Aw为壁面的面积;kC,H2O、EC,H2O和kC,CO2、EC,CO2为化学反应动力学参数，其数值如表1所示。

表1 热化学反应的动力学参数

通过计算隔层第一层网格单元内反应消耗碳的质量获得隔层表面的退移量dr，即

(6)

式中Vi为隔层表面第一层网格的体积；Li为该网格的边长；ρi为该网格的密度。

2.3 数值计算方法

上述隔层材料热解过程中能量扩散控制方程的求解主要是对扩散项进行离散，本文基于格心型结构网格有限体积法，通过空间二阶精度的中心差分格式，对控制方程中扩散项的温度偏导数采用Jacobian变化进行计算，时间推进采用三阶三步TVD型Runge-Kutta显式方法。此外，当隔层计算区域网格烧蚀退移时，计算区域网格会发生变形。因此，采用局部拉格朗日插值多项式插值方法对变形后网格的物理量进行插值。

3 隔层热解烧蚀过程计算结果分析

3.1 隔层计算模型

采用上述烧蚀计算模型，对Ⅰ脉冲工作热环境下EPDM隔层的热解烧蚀过程进行了研究。三维轴径混合隔层结构计算网格如图 6所示，隔层最大厚度为11 mm，隔层内部削弱槽宽度为2 mm，深度为1 mm，Ⅰ脉冲工作时间13 s，整个计算域采用结构网格，网格数量约为500 000。隔层靠近Ⅰ脉冲燃烧室外侧的为热流密度边界，贴近Ⅱ脉冲药柱和两个端面均设置为绝热壁，计算域初始温度为294 K。

图6 隔层结构传热烧蚀计算网格

3.2 隔层烧蚀计算结果分析

图 7为5 s时刻的隔层内部密度、热导率、温度分布。由于本文采用变热物性模型，因此隔层内部密度和热导率在不同位置处数值不同，这与采用常值的计算结果不同。在隔层轴向和径向的拐角处温度较高，此处隔层两侧均承受热载荷。此外，由于削弱槽深度较浅，未对温度的分布产生影响。

(a)Temperature contour

图8给出了Ⅰ脉冲工作过程中隔层过渡段局部切面上的温度变化过程。可见，在Ⅰ脉冲工作过程中燃烧室高温热流的作用下，随着时间的推移，隔层结构表面的温度从1 s时刻的1000 K逐渐升高到3500 K，与燃烧室的燃气温度相同。同时，随着隔层不断热解和炭化，热化学反应逐渐消耗隔层表面的炭化层，导致炭化层厚度逐渐减小。

(a)1 s (b)4 s

图9所示为隔层不同位置处温度随时间的变化历程，d为隔层深度位置，外表面d=0。由图9可见，不同位置处隔层的温度变化趋势差异较大，隔层外表面温度急剧增加后缓慢上升，隔层内部温度均缓慢增加，而隔层内表面靠近Ⅱ脉冲药柱处的温度未上升，表明隔层具有较好的绝热作用。图10所示为监测点隔层烧蚀量随时间的变化历程，监测点位置见图6。由图10可见，Ⅰ脉冲工作初期5 s内隔层烧蚀量缓慢增加，烧蚀速率仅为0.06 mm/s。但是，随着热流的持续作用，隔层的烧蚀量线性急剧增加，5 s至Ⅰ脉冲工作结束内的烧蚀速率达到了0.22 mm/s。

图9 隔层不同位置处温度的变化历程

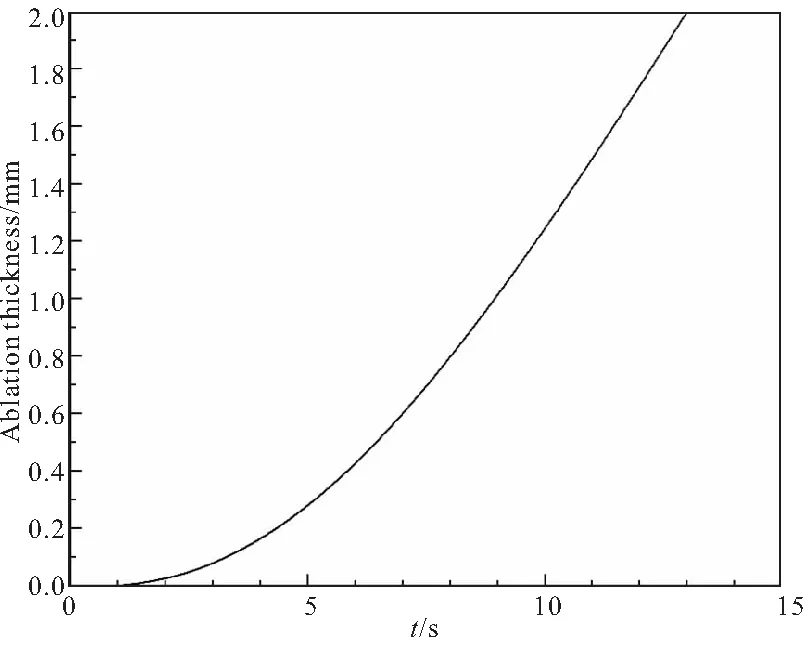
图10 隔层烧蚀量随时间的变化

4 隔层烧蚀结果的试验验证

为对双脉冲固体火箭发动机Ⅰ脉冲工作过程中隔层的烧蚀情况进行验证，设计双脉冲发动机隔层烧蚀模拟实验装置，隔层结构如图11所示。实验发动机结构与Ⅰ脉冲药柱燃烧温度、压力和质量流率与1.2节仿真边界条件一致。如图1所示，双脉冲发动机主要结构包括软质隔层、Ⅰ脉冲药柱、Ⅱ脉冲药柱、燃烧室壳体和喷管组件等，隔层右侧为Ⅰ脉冲药柱，左侧为Ⅱ脉冲药柱，隔层总厚度为11 mm。

图11 实验双脉冲发动机隔层结构

Ⅰ脉冲工作结束后隔层残骸解剖如图 12所示，隔层烧蚀情况测点分布见图 13。通过对解剖前后隔层进行测量，获得G1～G5隔层烧蚀数据，未发现隔层存在结构破坏现象，G1测点靠近筒段根部，最大烧蚀量为1.01 mm，最大烧蚀率为0.08 mm/s；G2测点在径向隔层中部位置，该位置最大烧蚀量为2.81 mm，最大烧蚀率为0.23 mm/s；G3测点在径向隔层靠近轴向隔层位置，该位置最大烧蚀量为2.64 mm，最大烧蚀率为0.21 mm/s；G4和G5测点几乎无烧蚀。进一步分析可知，隔层G2与G3测点烧蚀量较大，该位置位于隔层轴向与径向的过渡段。

图12 Ⅰ脉冲工作结束后隔层残骸解剖结果

图13 隔层烧蚀情况测量位置

根据上述双脉冲发动机隔层烧蚀模拟试验，Ⅰ脉冲工作13 s后，发现隔层烧蚀最严重的区域为轴向和径向的过渡段，最大烧蚀量为2.9 mm。为进一步重点详细分析该区域的传热烧蚀特性，并与试验结果进行对比，图 14给出了Ⅰ脉冲工作13 s后隔层的烧蚀区域与隔层传热烧蚀关键参数分布。可见，本文采用的变热物性模型准确获得了密度和比热容的非均匀分布，清楚地展示了炭化层、热解层、原始层三层结构。同时，试验测得隔层环向削弱槽附近烧蚀厚度为2.21 mm，计算得到的烧蚀厚度为2.0 mm，误差为9.5%，表明本文隔层烧蚀计算模型具有足够的精度。

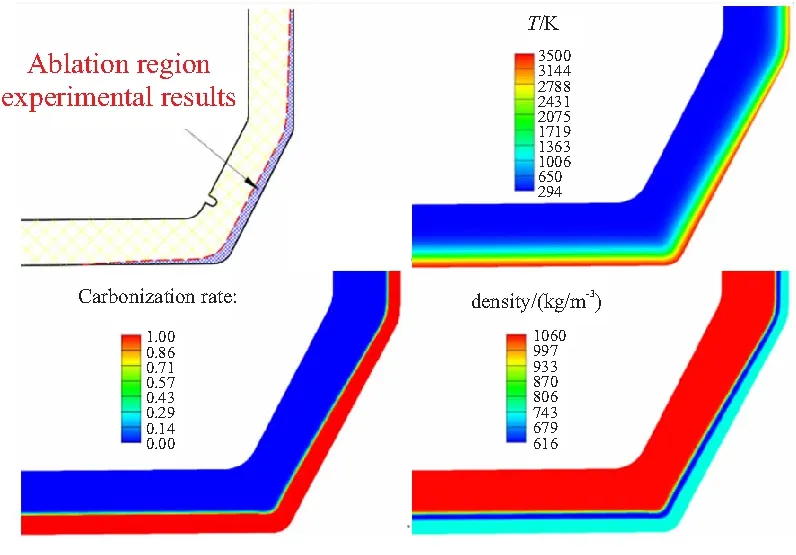
图14 Ⅰ脉冲工作13 s后实验结果和仿真云图

5 结论

(1)Ⅰ脉冲发动机工作过程中热流密度沿着隔层轴向逐渐升高，在轴向与径向的过渡段处达到最大值，隔层前后根部位置处的热流密度最小。

(2)Ⅰ脉冲工作初期隔，层外表面温度急剧增加，烧蚀量缓慢增加，随着热流的持续作用，隔层内部温度上升速率变缓，而隔层烧蚀量急剧增加。

(3)通过数值模拟发现，隔层轴向与径向的过渡段烧蚀较严重，与试验结果较吻合较好，表明了本文隔层烧蚀计算模型的准确性。