基于气流粉碎法的超细高氯酸铵粉碎工艺参数优化①

卢 翰，白鑫林，徐志刚，邱 磊，袁 潇

(1.中国科学院大学，北京 100049；2.中国科学院沈阳自动化研究所，沈阳 110016；3.中国科学院机器人与智能制造创新研究院，沈阳 110169；4.上海航天化工应用研究所，湖州 313002)

0 引言

固体推进剂满足能量高、成本低、推力大等优点，从而广泛地应用于武器装备以及火箭动力材料[1]。氧化剂作为固体推进剂中的重要组成部分为反应提供保障，而氧化剂材料种类繁多，常用的氧化剂材料有高氯酸铵(AP)、高氯酸锂、高氯酸钾、硝酸铵(AN)、二硝酰胺铵(ADN)、硝仿肼(HNF)等[2]。其中，在目前国际上最常使用的氧化剂的主要成分为AP，其在常温条件下物理性质十分稳定[3]，考虑到其强氧化性可能对温度的变化较为敏感，而事实上AP的温感情况为：在200～300 ℃发生低温分解，350～400 ℃发生高温分解，大于400 ℃快速燃烧甚至发生爆炸；根据真空安定性实验证明，其在150 ℃时也很安定[4]。而在固体推进剂中应用的氧化剂颗粒应满足一定的粒径要求，以确保在反应过程中得以充分进行。在颗粒粉碎领域有许多方法可以达到AP的粉碎要求[5]，如气流粉碎、机械粉碎法、化学粉碎法、超临界流体法等多种方法，但从环保、粉碎能耗以及粉碎质量等角度来看气流粉碎是最高效、清洁、成本低且质量高的方法。流化床气流粉碎技术广泛应用于化工、冶金、矿业、军工等领域的物料粉碎，其粉碎精度最高可达到0.1 μm，在生产超细粉体等领域发挥着重要的作用[6-7]。因此，本文采用流化床气流粉碎法对发动机氧化剂进行粉碎。

目前，对于超细粉碎技术的研究主要是进行单一因素的实验和分析，通常采用的方法也只是通过控制变量法或是简单的正交实验对工艺参数进行优化选择，但这些方法也只能选择出单一变量的最优求解区间而非最优解。NSGA-Ⅱ算法是使用精英策略的快速多目标优化非支配排序遗传算法，其寻优过程降低了计算的复杂度，可获取最优的Pareto前沿，且收敛速度更快[8-9]。

本文提出响应面法与NSGA-Ⅱ算法对氧化剂AP粉碎工艺参数进行优化。设计了单因素工艺实验，建立了多目标回归模型，分析了任意两因素构成的交互项对目标的影响，通过NSGA-Ⅱ算法高效搜索获取了全局最优参数集。

1 单因素实验

1.1 材料与设备

AP，粒径为60～80目，大连高佳化工有限公司。

QLD350氧化剂自动粉碎系统，上海细创粉体装备有限公司。

1.2 单因素实验及结果

流化床气流粉碎机的粉碎机理是通过喷射气流，将颗粒进行加速，通过颗粒间的相互碰撞实现破碎。因此，气流参数对粉碎效果有重要影响[10]。但对单因素实验而言，因为选择的是同种同型号的Laval喷嘴，故忽略气流入射速度的影响。

影响粉碎粒径分布于粉碎效率的因素有物理参数和工艺参数，本文主要研究的是工艺参数对于粉碎粒径分布和效率的影响。因此，不将氧化剂自身的物理性质考虑在内，并根据实际粉碎过程中涉及到的工艺参数进行单因素实验。

在单因素实验中，对粉碎腔压力、粉碎物重量和分级轮转速分别进行单因素实验，并以粉碎后颗粒粒径为响应值，考察各因素对响应值的影响，其实验参数如表1所示。粉碎压力、粉碎腔物料质量、分级轮转速的单因素实验结果如图1～图3所示。

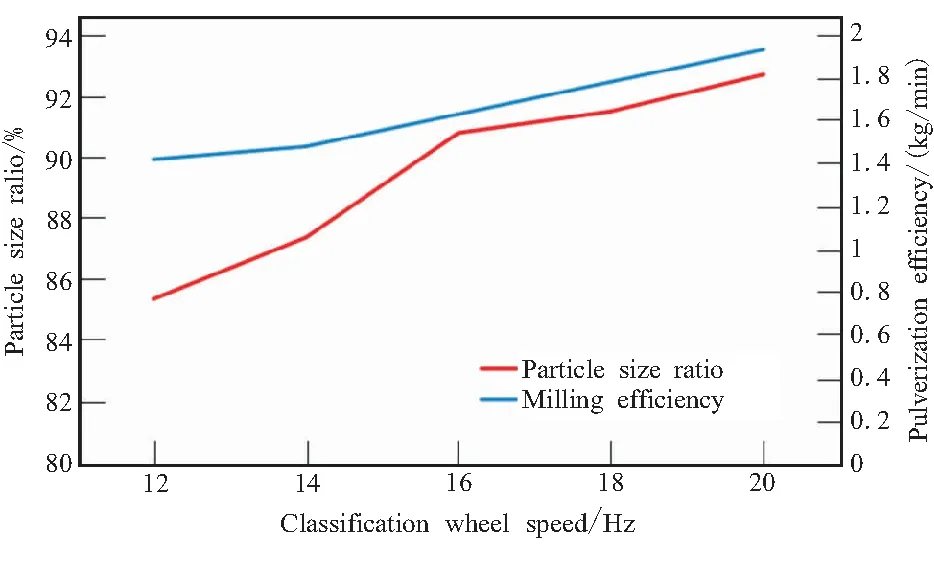
图3 分级轮转速单因素实验图

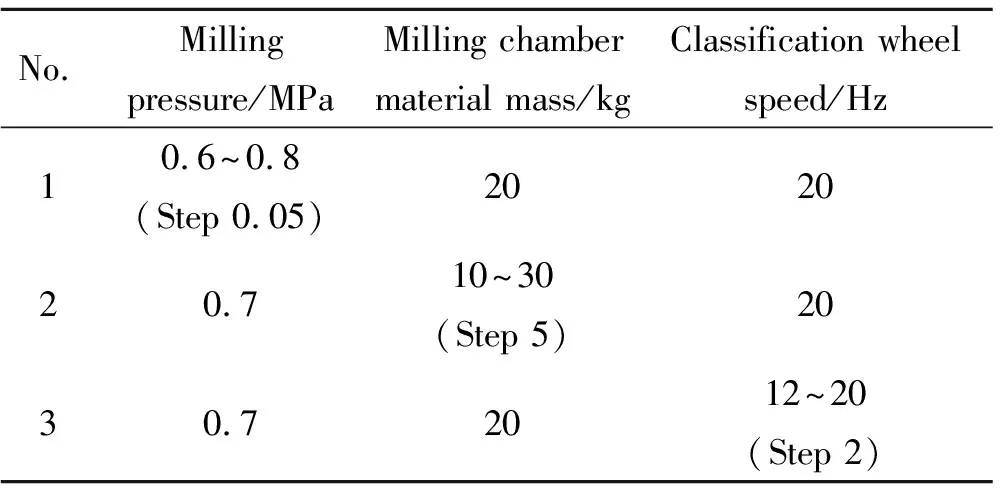
表1 单因素实验参数

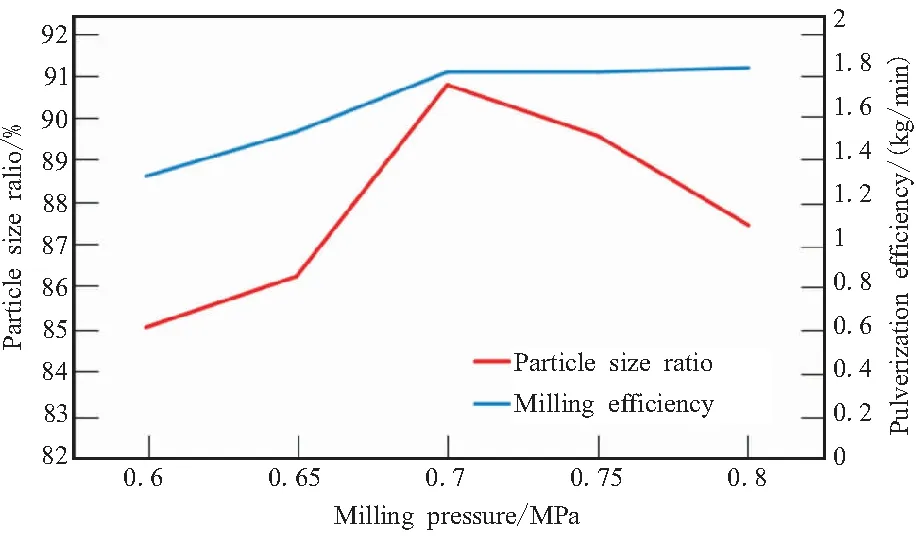
图1 粉碎压力单因素实验图

由图1可知，当压力大于0.7 MPa后，粒径占比明显下降，且粉碎效率也在0.7 MPa后基本保持稳定。因为粉碎压力的增大造成了细颗粒的团聚与粘结，使得细颗粒无法在分级轮处离开粉碎室，从而再次进入到粉碎室的循环中[11]。因此，在响应面实验中选择以0.7 MPa为中间水平。

由图2可知，随着粉碎腔物料重量的增大粒径占比与粉碎效率均有所增长，但粒径占比在20 kg后速率明显放缓。其原因在于：过高的物料质量提高了粉碎腔的滞留量，虽然提高了细颗粒的产生，但是也减小了粒子间的距离，使得颗粒运动速度下降，随之碰撞的频率和碰撞概率也受到限制[12]。根据设备实际的粉碎物料能力，同时为了获取较高的目标，选择25 kg为响应面实验中粉碎腔物料质量的中间水平。

由图3可知，分级轮转速对氧化剂粒径比率的影响与粉碎腔物料质量单因素实验曲线的趋势基本一致，在16 Hz处粒径占比出现拐点，而粉碎效率整体呈稳步上升趋势。该现象源于当分级轮转速过高导致在叶片附近形成团簇，团簇的粒子不能通过分级轮而进入再循环中，从而细颗粒被分级出的量有所下降，粒径占比增长受到制约[13]。由于粒径占比存在转折变化，因此选择转折附近的分级轮转速作为响应面实验的中间水平，并覆盖分级轮转速变化，选择10、15、20 Hz作为分级轮转速三个水平实验参数。

2 基于响应面法的工艺实验设计与分析

2.1 响应面实验设计

通过对不同工艺参数下粉碎结果进行取样，选取20 kg粉碎后的AP颗粒进行粒径分布的测量，图4所示为三组响应面水平对应的粒径分布情况，根据粉碎要求的粒径分布范围，选择了粒径中值位于5～10 μm的三组作为响应面实验的三组水平，并且选择了其中粒径分布最窄即粒径集中分布的一组作为响应面实验的中间水平。

图4 三组响应面水平对应的粒径分布

根据实际粉碎作业的要求选择粉碎腔压力(X1)、粉碎物质量(X2)和分级轮转速(X3)为自变量，以粉碎后颗粒粒径分布在5～10 μm内颗粒的占比(Y1)与粉碎效率(Y2)为响应变量，进行三因素三水平的响应面分析实验，建立粒径分布关于各影响因素的数学模型Y1(X1，X2，X3)和Y2(X1，X2，X3)。响应面实验中各因素水平参数如表2所示。响应面实验设计与结果如表3所示。

表2 响应面实验因素水平

表3 响应面实验设计与结果

2.2 多目标回归与方差分析

对Y1(X1，X2，X3)和Y2(X1，X2，X3)进行多因素回归分析，得到：

Y2(X1，X2，X3)=-380.3+280.93X1+28.22X2+

3.09X3+0.38X1X2+2.45X1X3-

(1)

Y2(X1，X2，X3)=-26.61+32.68X1+1.22X2-

0.02X3+0.16X1X2-

0.04X1X3+0.003X2X3-

(2)

对回归方程进行解析，可得到粒径分布占比和粉碎效率响应面多元回归模型方差，其结果分别如表4和表5所示。其中，粒径分布占比与粉碎效率的决定系数分别为0.892 7和0.956 9，证明了回归方程具有较高的可信度。

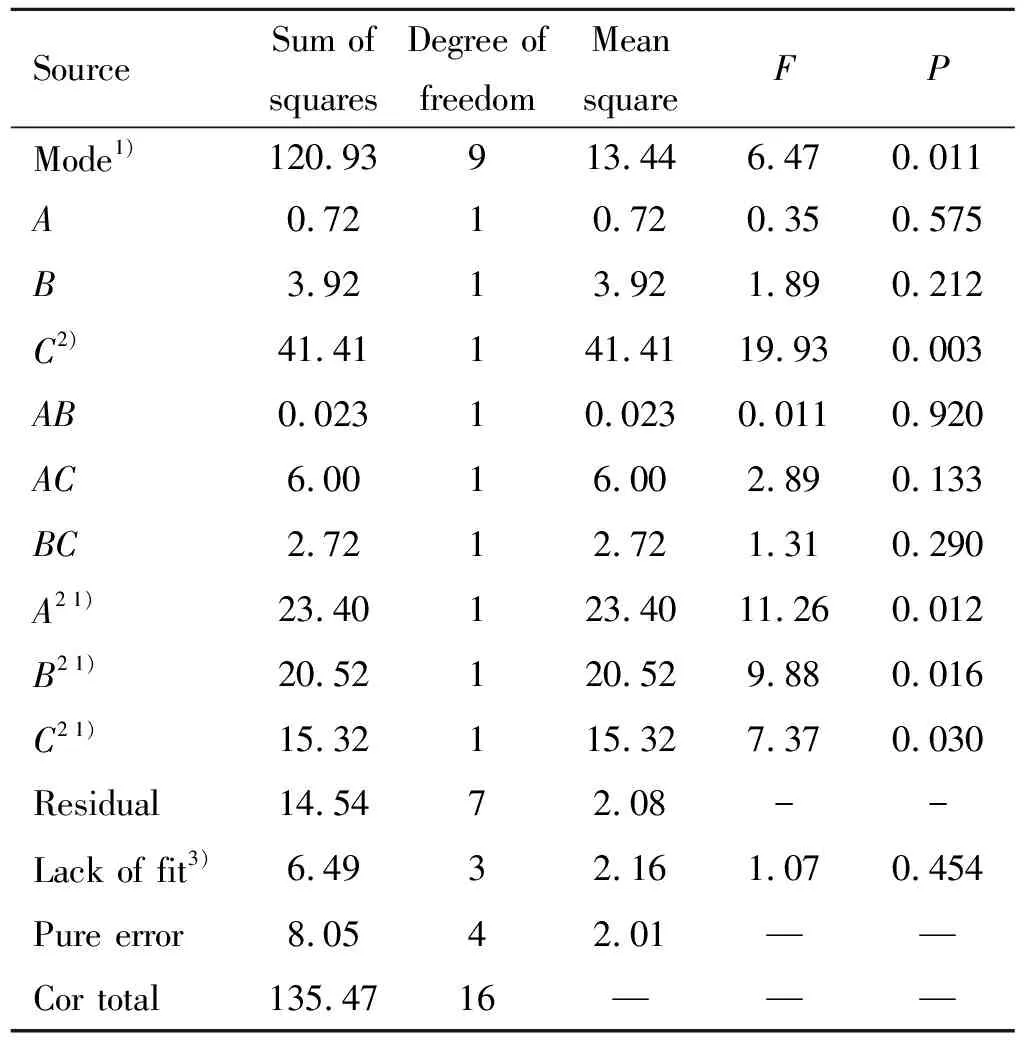
表4 粒径分布占比响应面多元回归模型方差分析结果

表5 粉碎效率响应面多元回归模型方差分析结果

由表中数据可知，对粒径分布占比和粉碎效率影响的主次顺序为分级轮转速(C)>粉碎腔压力(A)>粉碎物质量(B)，模型显著，失拟值不显著，表示该模型较为合理拟合度较高实验误差小。

对于粉碎腔压力(A)的增大则会使颗粒间的接触变得频繁，从而会造成细小颗粒的团聚，在一定范围内会由于接触频率的增大而使得粒径分布中值减小，但随着团聚现象的加剧，会造成粉碎的不充分，因此对于A和含有A的交互项不显著；但对于粉碎效率则由于二次粉碎使得颗粒粒径更细，因此A对粉碎效率的影响显著。

而粉碎物质量(B)对于粒径分布的影响，则是当颗粒总量增多，在一定范围内颗粒间的接触频率增大，但当物料重量过大，颗粒间距离缩小，使得颗粒碰撞破碎的效果减弱，并且颗粒大量集中在下部的粉碎区，由此粉碎效果也会下降，因此对于B和含有B的交互项不显著；对于粉碎物质量的增大也会使最终产生的粉碎产物增多，从而B对粉碎效率的影响显著。

2.3 响应面交互作用分析

结合对于粒径占比与粉碎效率的要求，获取响应面实验交互作用，分别如图5～图7所示。图中各曲面均为凸曲面，因此交互作用较为明显。

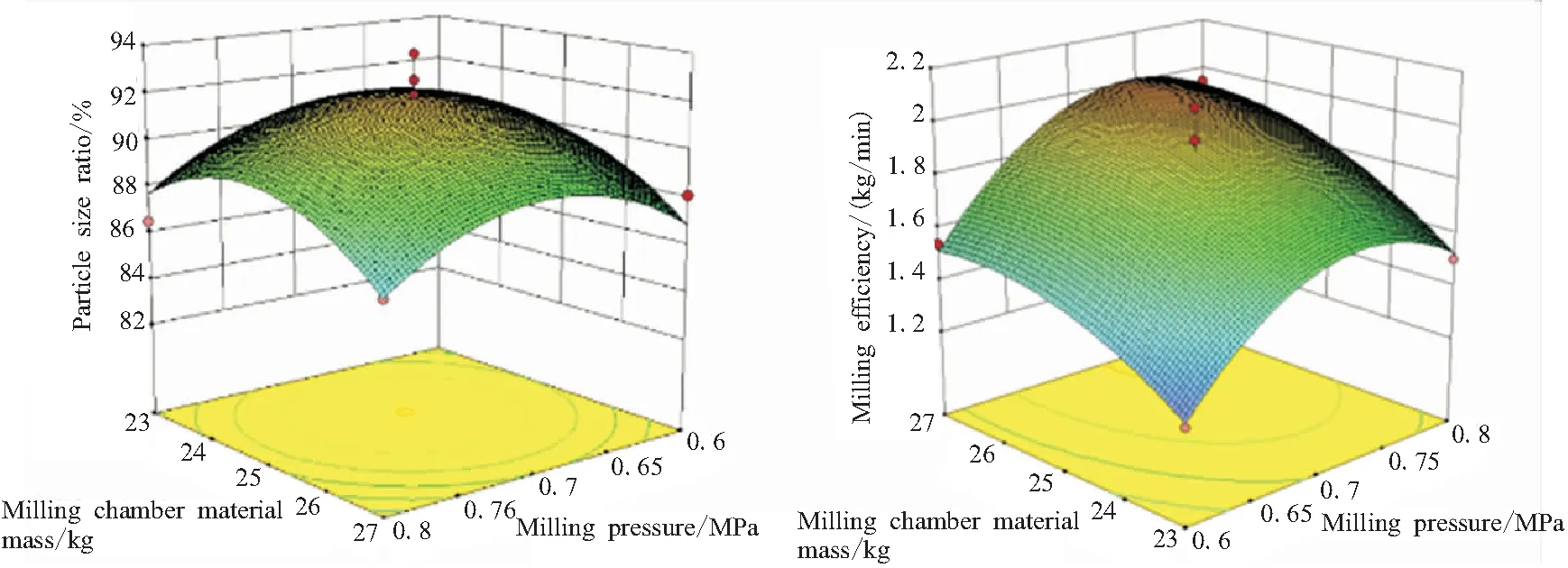
(a)Particle size ratio (b)Milling efficiency

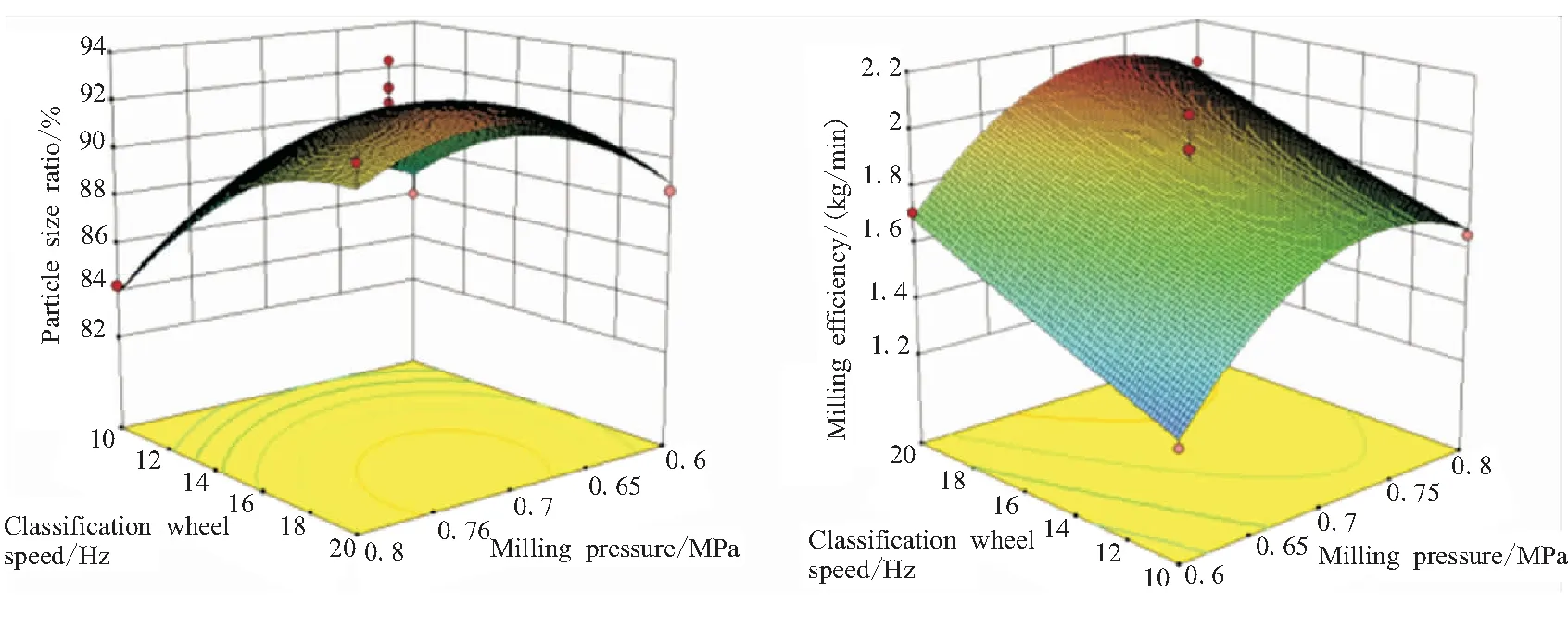
(a)Particle size ratio (b)Milling efficiency

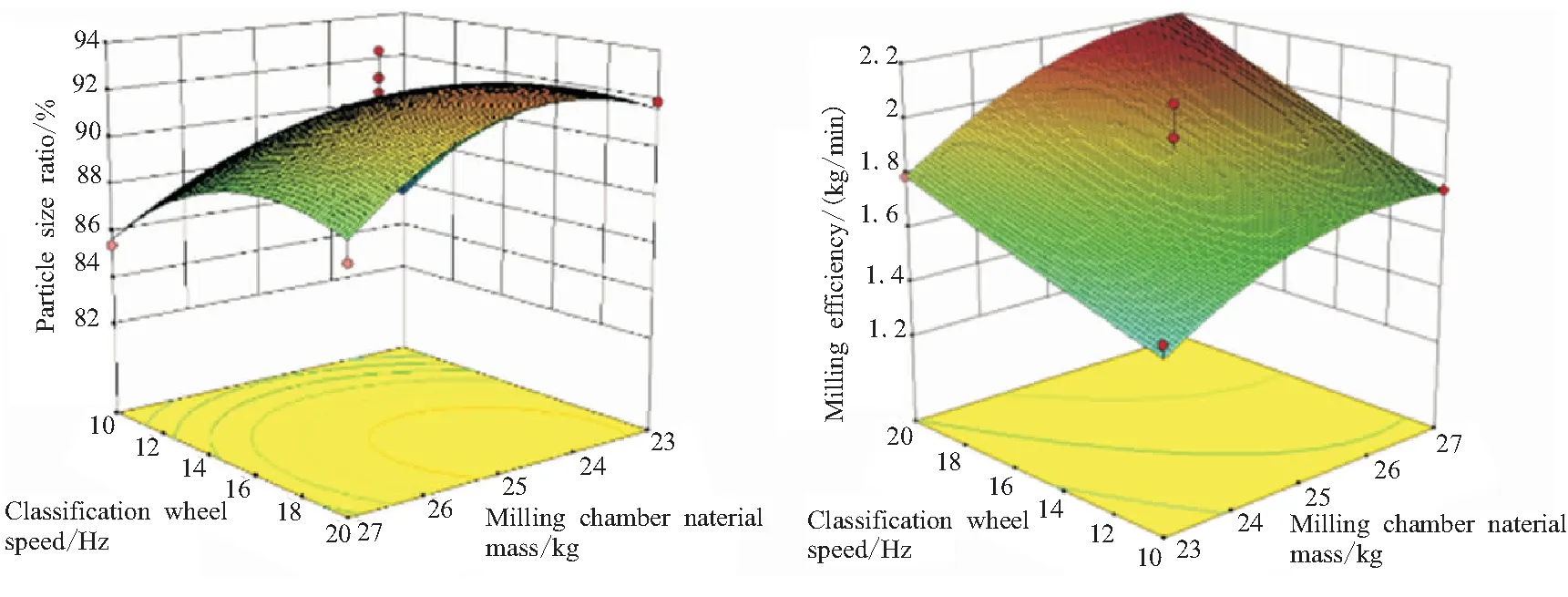
(a)Particle size ratio (b)Milling efficiency

对粉碎腔压力与粉碎物质量的交互，粒径分布呈现中间隆起，其对应等高线的最高点为两因素最适范围的交汇处。而粉碎效率则是受两因素的共同影响由低到高变化，当超过两因素最适范围后，粉碎效率也随之下降。对粉碎腔压力与分级轮转速的交互，粒径分布响应面以及粉碎效率响应面和其对应的等高线均呈现向分级轮转速增大一侧和粉碎腔压力最适范围处集中的现象，这是由于分级轮转速的增大促进了细颗粒的排出从而使得粒径分布与粉碎效率在分级轮转速最大时达到较高水平。对粉碎物质量与分级轮转速的交互，粒径分布响应面以及粉碎效率响应面和其对应的等高线均呈现向分级轮转速增大一侧集中的现象，但对于粒径分布则是在粉碎腔物料质量最适范围处，而粉碎效率则是在粉碎腔物料质量最大时达到最高水平，这是因为虽然物料质量过大使得粉碎效果变差，但同样时间产生细颗粒的量也随之增大，从而会在一定程度上提高粉碎效率。这也与上文的分析相符合。

3 NSGA-Ⅱ算法优化工艺参数

3.1 NSGA-Ⅱ优化流程

图8所示为NSGA-Ⅱ优化流程，当设置好种群情况以及迭代的参数后，即可进行NSGA-Ⅱ算法优化。首先快速非支配排序，再通过计算解i的被支配个数ni以及由i支配的一组解集Si，依次对种群内所有个体进行划分，将同一支配等级的个体放入集合Fi中，直到种群中个体的等级被完全划分[13]。

之后，进行拥挤度计算以及比较拥挤算子，某一个体的拥挤距离是指由该个体两侧个体构成的矩形的平均边长，如图9所指示，位于首尾两端个体的拥挤距离为无穷大。

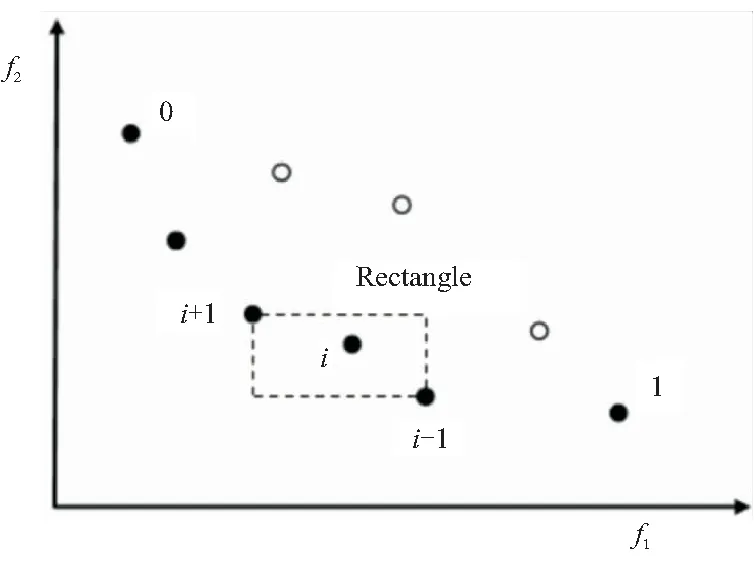
图9 拥挤距离计算方法示意图

其余个体的拥挤距离计算方法为

(3)

拥挤比较算子式是基于每个解的Pareto等级以及拥挤距离定义的，对于每个个体i都具有它自身的非支配等级irank以及拥挤距离idistance，通过irankjdistance)确定一个偏序关系i≥j。若支配等级不同则选择支配等级低的个体，若支配等级相同则选择拥挤距离大的个体。

而对遗传环节中的选择部分使用二元锦标赛选择方法(BTS)，二元锦标赛选择方法(BTS)是指从父代中随机选择2个个体，比较两者的适应度，选择适应度比较大的个体参与交叉与变异，另一个淘汰。

交叉部分选择二进制交叉算子(SBX)，二进制交叉(SBX)是模拟二进制字符串的单点交叉，两个父代x1和x2经过交叉后产生两个子代y1和y2，并且父代中的信息得以保留到下一代中。x1(i)和x2(i)为对应个体的i段基因，选取0到1间的随机数μ，计算交叉系数α，其值为

(4)

式中η为分布因子，且分布因子越大，子代继承父代的基因越多。

交叉后的子代片段分别为

y1(i)=0.5[(1+α)x1(i)+(1-α)x2(i)]

y2(i)=0.5[(1-α)x1(i)+(1+α)x2(i)]

(5)

变异部分则选择单点变异算子，单点变异是根据随机生成的数据对基因中的某个点位进行改变，并且变异的概率受到预设的变异系数所影响。

设置决策变量为：X1粉碎腔压力、X2粉碎物质量和X3分级轮转速。边界条件分别为0.6≤X1≤0.9；23≤X2≤27；10≤X3≤20。种群规模为50，最大迭代次数为200，目标分别为Y1与Y2。

3.2 NSGA-Ⅱ优化解集

利用MATLAB软件实现NSGA-Ⅱ的优化过程，获得图10所示的Pareto前沿面。

由图10所示的前沿面显示，在粉碎效率较高的部分(1区)粒径占比极低，而在粒径占比较优的部分(3区)粉碎效率衰减的极快。为了兼顾粉碎效率与粒径占比，并且同时考虑决策变量的取值区间，故应该在粉碎效率与粒径占比均处于较高水平的2区寻找最优解，但同时考虑到粒径对于颗粒粉碎的直接衡量指标，因此可以在取值时适当放宽对于粉碎效率的要求，所以对于2区与3区交界的个别解也在选择范围内。

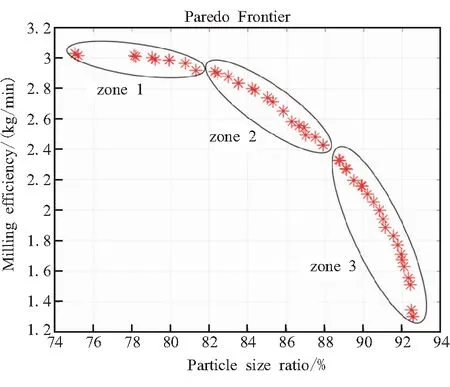
图10 Pareto前沿面

根据上述要求条件，获取多目标优化的Pareto解集，如表6所示。

表6 多目标优化获取的Pareto解集

3.3 NSGA-Ⅱ算法优化结果分析

氧化剂粉碎工艺参数多目标优化获取的Pareto解集提取出的最优条件为粉碎压力0.74 MPa，粉碎腔物料重量25.10 kg，分级轮转速14.90 Hz。该情况下获得的粒径分布为91.16%，粉碎效率为1.90 kg/min。考虑到实际的参数调节范围，对工艺参数进行取整，则粉碎压力为0.70 MPa，粉碎腔物料重量为25.00 kg，分级轮转速为15.00 Hz。

根据实际的样机实验反馈的数据显示，使用NSGA-Ⅱ算法优化的工艺参数：粉碎压力为0.70 MPa，粉碎腔物料重量为25.00 kg，分级轮转速为15.00 Hz，进行样机实验得到的粒径分布为90.70%，粉碎效率为1.95 kg/min。由样机实验结果与NSGA-Ⅱ算法计算结果对比可知，粒径分布相似度99.50%，粉碎效率相似度97.44%，并且其计算工艺参数与实验工艺参数匹配度在94.60%以上，验证了优化模型的准确性和计算方法对氧化剂粉碎工艺参数优化的有效性。

4 结论

(1)通过对氧化剂AP粉碎工艺参数进行采集与分析，以单因素实验为基础，通过响应面分析选取了较为适宜的数值域，建立了有效的响应面模型，为氧化剂多目标优化提供了有效的数据基础。

(2)通过NSGA-Ⅱ算法对响应面法获得工艺实验数据进行多目标寻优，获取了Pareto前沿解集，使用优化的计算工艺参数进行样机实验。结果表明，实验工艺参数得到的粒径分布相似度99.50%，粉碎效率相似度97.44%，工艺参数匹配度在94.60%以上，验证了所提出方法的有效性。

所提出的方法可适应氧化剂粉碎过程更复杂的工艺参数优化，在一定程度上减少了实验成本，为氧化剂粉碎工艺参数的优化提供了新的思路。