多孔U-10Zr金属燃料热学及力学性能的有限元计算①

赵瑞瑞，贾寅峰，刘卓扬，齐永良，张旭东，邓俊楷*，李国庆

(1.中核北方核燃料元件有限公司 中核新型材料研究与应用开发重点实验室，包头 014035；2.西安航天复合材料研究所，西安 710025；3.西安交通大学 金属材料强度国家重点实验室，西安 710049；4.西安交通大学 网络信息中心，西安 710049；5.西安卫星测控中心，西安 710079)

0 引言

金属燃料由于具有中子经济性好、裂变核素密度高、热导率高、易于后处理等优点，因而是先进轻水堆和钠冷快堆等堆型的重要新型燃料材料。国内外针对压水堆用金属燃料开展了诸多研究，包括U-Zr合金、U-Zr-Hx合金、U-Mo合金等。其中U-Zr金属燃料的应用成为行波堆、钠冷快堆燃料的重点方向[1-3]。

在反应堆中，核燃料元件处于苛刻的工作环境之中，在堆内运行过程中产生复杂的辐照-热力耦合行为。燃耗初期，核燃料产生裂变热，导致燃料元件内部出现比较大的温度变化，从而产生热应力；随着燃耗的发展，燃料元件内产生固体和气体裂变产物，它们的体积大于裂变之前的物质的体积，燃料元件的体积随着燃耗发展而增大，称为辐照肿胀。核燃料的辐照肿胀导致燃料芯块与包壳相互作用，引起包壳管的径向变形和横向拉伸，造成包壳管破损，严重威胁反应堆的安全运行[4]。针对这一问题，目前提出一种新的思路，设计多孔金属燃料，在金属燃料芯块内部预置一定数量、分布的孔隙，降低金属燃料芯块本身有效密度，贮存裂变气体，为燃料体积膨胀预留空间。然而，所设计的多孔金属材料必须满足一定的传热和力学性能的要求，才能在实际的反应堆中获得应用[5]。目前，研究人员已制备了多孔 U-10Zr金属燃料芯体，通过调整烧结温度与烧结时间，可获得不同孔隙率[6]。但目前对多孔U-10Zr合金热学及力学性能与孔隙率之间关系缺少系统研究。

有限元模拟方法是揭示材料结构-性能关系的有效方法[7-10]。因此，本研究工作针对U-10Zr金属燃料，利用有限元模拟方法建立不同孔隙率的代表性体积单元模型，开展热学及力学性能的模拟计算，阐明多孔U-10Zr金属燃料中孔隙率对其热学性能和力学性能的影响规律。结果表明，通过控制U-10Zr合金孔隙率可有效调控其热学及力学性能，使其有望在新型反应堆金属燃料中取得应用。

1 多孔U-10Zr合金有限元模型

首先，根据多孔U-10Zr材料微结构特征，建立起多孔相的几何结构模型。多孔相为六棱柱形貌，通过Python程序控制多孔相在基体中的取向及分布具有随机性，并允许孔洞相互穿透交叉进而形成更加复杂的多孔形貌。随后，构建立方体有限元模型作为多孔U-10Zr材料的代表性体积单元。基于图1(a)中的多孔U-10Zr合金的微结构照片[11]，利用上述方法与技术构建了具有周期性几何特征的多孔U-10Zr材料有限元模型，如图1(b)所示。

(a)Microstructure[11] (b)Finite element model

同时，为研究孔隙率对多孔U-10Zr材料热学及力学性能的影响，构建了孔隙率为5%～30%的6种多孔U-10Zr金属燃料有限元模型(图2)。模拟所构建的有限元模型中孔隙平均尺寸为1 mm，代表性体积单元长宽高均为5 mm。经测试，该模型规模能满足计算结果收敛性要求。同时，对所有模型均划分了精细网格，且网格数量随着孔隙率增加而增加，当孔隙率为30%时，网格数量约为135 000，能够保障计算结果准确性[12]。

图2 不同孔隙率的多孔U-10Zr材料有限元模型

2 计算方法与参数

2.1 多孔U-10Zr金属燃料热导率计算

热导率是燃料设计和反应堆分析的重要物理参数。因此，对多孔U-10Zr金属燃料的热导率进行研究至关重要。模拟用了稳态热传导方法，对有限元模型上、下两侧分别施加0 K和100 K的温度边界条件来形成温度梯度，网格类型为四面体四节点的线形传热单元(DC3D4)。利用傅立叶公式推导热流密度计算公式为

λ=-qT/(dT/dr)

(1)

式中λ为材料的热导率，W/(m·K)；T为沿着热传导方向的温差，K；q为热流密度，J/(m2·s)；dT/dt为温度梯度，K/m。

在对多孔U-10Zr合金进行了稳态热传导分析之后，利用 Python程序对稳态热分析结果进行后处理。首先，通过体积均分方法统计了所有单元的热流密度平均值；随后，对温度梯度进行计算；最后，通过式(1)得到多孔U-10Zr合金的热导率。

对于块体U-10Zr材料，其热导率符合式(2)[13]：

λ=3.26631×10-6T2+2.24774×10-2T+9.62036

(2)

由式(2)可以确定U-10Zr材料在300、600 K时的热导率分别为16.658、24.283 W/(m·K)。模拟中，孔隙的热导率为0。

2.2 多孔U-10Zr金属燃料热膨胀性能计算

材料受热而产生变形同样是合金燃料设计和反应堆分析的重要考量。因此，利用有限元模拟实现对材料热膨胀性能的模拟计算具有重要的意义。在对多孔U-10Zr合金的热膨胀系数进行计算时，施加周期性边界条件。设置了模型在初始时整体温度为0 K，随后整体升温至300 K。经计算后，测量模型随温度变化而产生的尺寸变化，从而计算其热膨胀系数。周期性边界条件[14-15]可写为

(3)

计算热膨胀系数公式[16]如式(4)所示：

(4)

式中 ΔL为在ΔT温度范围内模型尺寸变化；L0为模型初始尺寸。

模拟中，U-10Zr合金300 K时的热膨胀系数为1.261×10-5K-1。通过有限元计算，利用Python程序通过体积均分法统计模型所有单元上的位移变量，最后通过式(4)得到多孔U-10Zr金属燃料的热膨胀系数。

2.3 多孔U-10Zr金属燃料力学行为计算

对于多孔U-10Zr材料的力学行为，有限元模拟时，对模型施加周期性边界条件及适当压缩载荷。模拟中，网格类型为C3D4。通过有限元计算，利用Python程序通过体积均分方法获得多孔U-10Zr材料应力-应变力学响应[17-18]。模拟中块体U-10Zr金属燃料的弹性模量为17.12 GPa，泊松比0.31，屈服强度约为801 MPa，断裂应力为1115.552 MPa。依据相关实验数据，获得了相关的有限元塑性参数，如表1所示。

表1 U-10Zr材料的有限元模拟塑性参数

3 结果与讨论

3.1 孔隙率对多孔U-10Zr金属燃料热导率影响

图3为有限元模拟得到的多孔U-10Zr金属燃料在300、600 K时的热导率随孔隙率变化规律。

图3 不同孔隙率U-10Zr材料在300、600 K时的热导率

可以看到，计算的块体(0%)U-10Zr金属燃料热导率与预设值一致，证明了模拟方法的准确性。高温下多孔U-10Zr材料始终展现出更优的导热性能，同时热导率随孔隙率增加而线性下降。300 K时，当多孔U-10Zr材料孔隙率增加至30%时，其热导率由块体时的16.66 W/(m·K)下降至8.8 W/(m·K)。而在600 K下，当多孔U-10Zr材料孔隙率增加至30%时，其热导率由块体时的24.28 W/(m·K)下降至12.83 W/(m·K)，降幅更加显著。

根据最小热阻力原理，热传导过程中热流会优先流向热阻最小的通道。因此，由不同孔隙率的U-10Zr多孔材料热流密度云图(图4)可以看到，当热流经过，热流主要流向热阻小的相，即热导率高的相，热流汇聚，热流密度增加。而在孔洞处，热导率为0，因此无热流通过。孔洞缺陷的存在，改变了热流密度在复合材料中的分布。对比300 K(图4(a))与600 K(图4(b))下热流密度分布云图可以看到，由于U-10Zr材料600 K下的热导率显著高于300 K时，因此多孔结构中的热流密度整体也显然更高。

(a)300 K (b)600 K

3.2 孔隙率对多孔U-10Zr金属燃料热膨胀性能的影响

孔隙率对多孔U-10Zr热膨胀系数的影响如图5所示；不同孔隙率的多孔U-10Zr热膨胀应力云图如图6所示。

图5 孔隙率对多孔U-10Zr热膨胀系数的影响

图6 不同孔隙率的多孔U-10Zr热膨胀应力云图

由图5可见，计算的块体(0%)U-10Zr金属燃料热膨胀系数与预设值一致，证明了模拟方法的准确性。U-10Zr材料的热膨胀系数随孔隙率的增大而显著下降。孔隙率增加至30%时，其热膨胀系数由块体时的1.261×10-5K-1下降至0.883×10-5K-1，有利于其抗热震性。

由图6可以看到，由于U-10Zr合金的热膨胀系数仅为1.261×10-5K-1，仅受热而产生的内应力较小。但随着孔隙率的增加，多孔U-10Zr合金内部应力逐步增加，局部出现明显的应力集中。这主要是由于孔隙率增加导致的结构缺陷所引起的，但整体上，内应力均处于较低数值。

3.3 孔隙率对U-10Zr金属燃料力学行为的影响

基于块体U-10Zr材料的压缩应力-应变曲线，模拟了块体U-10Zr材料的压缩过程的力学响应，结果如图7所示。可以看到，在块体U-10Zr材料压缩弹性变形阶段以及随着载荷增加产生屈服后的塑性变形阶段，有限元模拟结果与实验结果均吻合较好，证明了模拟方法的有效性。

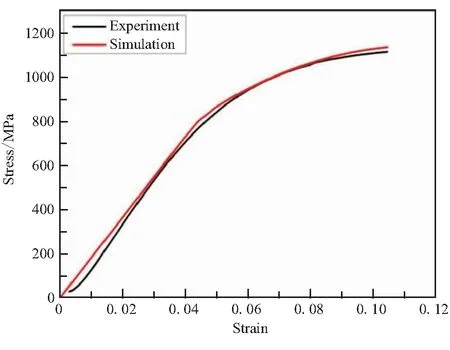
图7 块体U-10Zr的压缩应力-应变曲线

基于不同孔隙率的多孔U-10Zr材料模型与块体U-10Zr的材料参数进行压缩实验的有限元模拟，得到不同孔隙率U-10Zr金属燃料压缩力学响应如图8所示。可以看到，孔隙的存在对U-10Zr材料力学性能有较大影响，多孔U-10Zr材料的弹性模量、屈服强度和断裂强度随孔隙率的增大而减小。当孔隙率达到30%时，U-10Zr材料的弹性模量由块体时的17 120 MPa下降至7780 MPa，屈服强度由801 MPa下降至304 MPa，而断裂强度由1116 MPa下降至327 MPa。统计结果如表2所示。孔隙率增加使材料性能下降的直接原因为缺陷导致局部应力集中，从而使材料微结构过早发生失效[19]。

表2 U-10Zr不同孔隙率的多孔U-10Zr材料力学性能

图8 不同孔隙率的多孔U-10Zr材料的应力-应变曲线

对比不同孔隙率U-10Zr金属燃料在其应力-应变曲线上发生宏观塑性变形时的应力状态可见(图9)，在低孔隙率时(5%、10%)，发生屈服时多孔U-10Zr材料内部有较多区域(黑色)应力超过屈服点，发生了塑性变形。随着孔隙率增加，多孔U-10Zr宏观屈服所对应的多孔材料内部应力分布越发不均匀，应力集中越发明显，屈服区域越来越集中，塑性变形甚至集中在非常狭小的区域，而这些区域可认为是裂纹萌发和失效产生的区域。孔隙率增加导致愈发严重的应力集中，有待进一步从孔洞形貌、分布等的优化方面进行研究。

由图8还注意到，孔隙的存在也使得多孔U-10Zr应力应变曲线在屈服及之后的塑性阶段力学响应更加平滑。如图10(a)所示，选取了20%孔隙率U-10Zr材料应力-应变曲线上a、b、c、d四个点处的等效塑性应变(PEEQ)(图10(b))。a、b、c、d点处的宏观应变分别为0.041、0.048、0.056、0.064。

(a)Stress-strain curve

通过对比可以看到，多孔U-10Zr材料中发生不均匀变形，在多孔U-10Zr材料宏观上屈服之前，材料内部已经有区域发生塑性变形(宏观应变0.041，a点)。随着应变持续增加，发生塑性变形区域增加且程度累积，部分区域发生严重的塑性变形，从而导致多孔U-10Zr材料最终损伤失效。

4 结论

(1)孔洞缺陷的存在，改变了U-10Zr金属燃料中热流密度分布，随着孔隙率增加，U-10Zr金属燃料的热导率下降。当孔隙率达到30%时，多孔U-10Zr合金的热导率降幅约为47%。

(2)孔洞缺陷的存在，使得U-10Zr金属燃料中存在应力集中，U-10Zr金属燃料的力学性能随着孔隙率增加而下降。当孔隙率达到30%时，其弹性模量、屈服强度与断裂强度分别下降至7.78 GPa、303.95 MPa、326.55 MPa。

(3)孔隙率增加使U-10Zr金属燃料热膨胀系数降低。孔隙率为30%的多孔U-10Zr合金的热膨胀系数仅为0.883×10-5K-1。因此，其结构内部由热膨胀导致的应力集中整体较小。