输油管道池火灾事故后果不确定性分析

徐婧源 ，陈敬东，王乾儒，陈华燕

1.中国石油西南油气田分公司集输工程技术研究所，四川 成都 610041

2.油气藏地质及开发工程国家重点实验室·西南石油大学，四川 成都 610500

3.电子科技大学信息与通信工程学院，四川 成都 611730

4.四川大学建筑与环境学院，四川 成都 610065

引言

池火是导致输油管道发生火灾爆炸事故、进而引发次生灾害的主要原因之一，科学准确地评估池火灾的危害区域对应急预案制定及救援工作开展具有现实指导意义。然而，受大气环境、油品介质和泄漏量等事故变量和气象变量的影响，池火灾发生及其事故后果存在极大的不确定性[1-6]，充分考虑各变量的不确定性，才能避免事故后果分析的片面性，从而为管理决策提供可靠依据。

目前，有关池火灾事故后果的分析通常采用控制变量法对预先设定好的灾害场景进行伤害范围计算。孙东亮等[7]预设风速范围为0.57～2.00 m/s，分析了直径在0.57～2.00 m 的航空燃料池火的燃烧速率。邝辰[8]假设环境风水平作用，研究了0.25、0.35 和0.45 m 等5 种油池边长和0、0.50 和0.96 m/s等11 种风速条件下，池火燃烧速率和辐射热流密度演变规律。刘彦麟[9]分析了风速取值1.50、3.00 和5.00 m/s，泄漏孔径5、25 和100 mm 时，SL 机场机坪管道池火灾热辐射影响区域变化情况。郑昕[10]利用CFD 软件分别分析了围堰直径35 m 时风速对LNG 池火火焰的影响规律以及风速9.60 m/s 时围堰直径对LNG 池火火焰的影响规律。朱建华等[11]以苯池火为研究对象，计算了液池半径20 m、环境温度15°C、风速4.00 m/s 条件下，苯池火热辐射伤害范围。谢顶杉等[12-13]采用单因素分析法分别研究了风速、围堰尺寸等因素对热辐射距离的影响规律。

可见，现有研究由于没有考虑到池火灾事故的突发性和随机性，导致事故后果分析难以准确全面，为此，本文针对输油管道选取液池直径、燃烧速率和风速3 个对池火热辐射通量影响较大的因素为不确定性参数，建立了输油管道池火灾事故不确定性分析模型，以某输油管道为例确定各不确定性参数的取值范围并采用拉丁超立方抽样法获取30 000个随机组合样本，利用蒙特卡洛法[14-19]分析池火热辐射通量分布特征，得到距事故点不同位置处池火灾致死率的统计规律。

1 输油管道池火灾不确定性分析模型

池火灾的数学模型主要包括场模型和半经验模型两类，场模型比半经验模型具有更高的置信度，但是场模型的缺点在于需要专业人员并且工作量大，不适宜现场工程技术人员使用。半经验模型是基于火灾实验数据而得到的经验公式，采用无因次关系式描述火灾特征，具有模型相对简单、使用方便并且预测结果合理等优点，更多地使用在工程风险评价中[20-21]。选用Mudan 模型计算池火灾热辐射强度，该模型将火焰看作圆柱形，是目前应用最广的池火计算模型[22-23]。

半经验模型中的池火辐射通量的计算分为以下3 个部分[23-25]：（1）计算池火形状（高度）；（2）计算表面辐射率；（3）计算热辐射通量。

1.1 池火高度

（1）风速等级

式中：--u*风速等级，无因次；

uw--风速，m/s；

uc--特征风速，m/s；

g --重力加速度，g=9.8 m/s2；

m′′--静止空气中物质的燃烧速率，kg（/m2·s），该值大小与物质种类和液池直径有关，计算方法参见文献[25]；

D--液池直径，m；

ρair--气体密度，kg/m3。

（2）火焰的平均高度

式中：L--火焰的平均高度，m。

1.2 表面辐射率

假定能量由圆柱形火焰侧面和顶部向周围均匀辐射，计算火焰表面的热通量

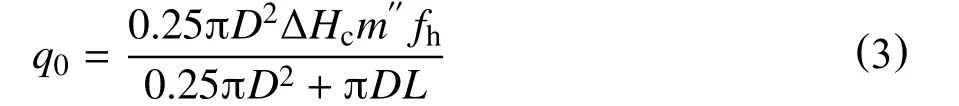
式中：q0--火焰表面的热通量，kW/m2；

ΔHc--燃烧热，kJ/kg；

fh--热辐射系数，kW（/m·K）。

1.3 热辐射通量

（1）目标接收到的热通量

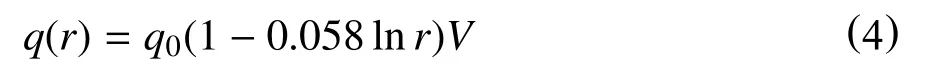
式中：

q(r)--目标接收到的热通量，kW/m2；

r--目标到泄漏中心的水平距离，m；

V—视角系数，无因次。

（2）计算视角系数

视角系数V的大小取决于目标到火焰垂直轴的距离与火焰半径之比s和火焰高度与直径之比h

式中：s— 目标到火焰垂直轴的距离与火焰半径的比值，无因次；

h—火焰高度与直径之比，无因次；

A，B，a，b，J，K，VH，VV— 为描述方便而引入的中间变量。

2 输油管道池火灾事故不确定性分析

2.1 场景描述

以某输油管道为例，利用蒙特卡洛法计算管道池火灾热辐射通量分布特征，分析与事故点不同距离处池火灾致死率统计规律。该管道全长31 km，管径406.4 mm，设计压力4.0 MPa；管道途经地区年平均风速2.50 m/s，年均气温23°C。

Mudan 模型中热辐射通量计算与液池直径、燃烧速率和风速紧密相关，因此，输油管道池火灾后果分析选取液池直径、燃烧速率和风速为不确定性参数，各参数的随机分布特征结合工程实例由对应的概率密度函数给出[23，26-27]

式中：Normal—正态函数。

各不确定性参数累计概率分布见图1。

图1 池火灾事故不确定性参数累计概率分布Fig.1 Cumulative probability distribution of uncertain parameters of pool fire accident

2.2 参数敏感性分析

池火模型中液池直径、燃烧速率和风速3 个参数相互关联，共同影响输油管道热辐射通量，因此，对3 个参数进行参数敏感度整体分析，考察3 个参数在指定范围内同时变化时对热辐射通量的影响程度。参数取值如表1 所示。

表1 参数敏感度分析中各参数取值范围Tab.1 Value range of each parameter in sensitivity analysis

2.2.1 拉丁超立方抽样

采用拉丁超立方抽样法，分别在3 个不确定性参数的取值区间对应的三维空间中随机抽取300、1 000 和2 000 个样本，3 个不确定性参数的样本分布如图2～图4 所示。

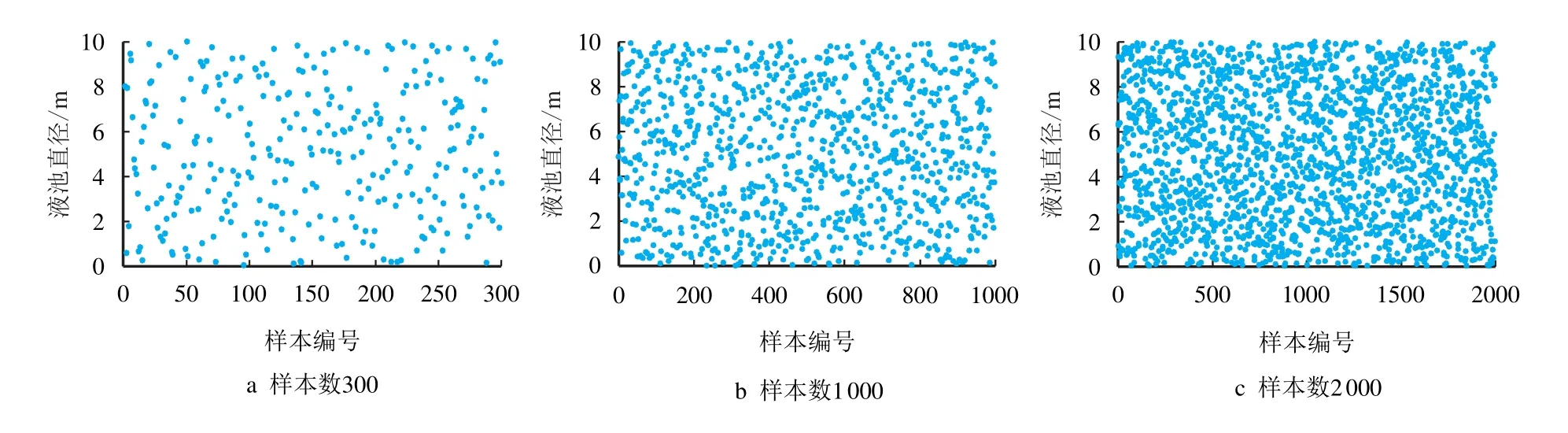
图2 池火灾事故不确定性参数液池直径样本分布Fig.2 Sample distribution of pool diameter for uncertain parameters of pool fire

图3 池火灾事故不确定性参数燃烧速率样本分布Fig.3 Sample distribution of combustion rate of uncertain parameters of pool fire

图4 池火灾事故不确定性参数风速样本分布Fig.4 Wind speed sample distribution of pool fire accident uncertainty parameter

2.2.2 不确定性参数秩相关系数计算与分析

采用Spearman 秩相关系数分析法计算3 个不确定性参数同时变化时，各不确定性参数对目标函数池火热辐射强度的影响程度[26-27]，如表2 所示。

从表2 可以看出，样本数为300 得到的3 个不确定参数Spearman 秩相关系数排序规律与样本量为1 000 和2 000 时的计算结果相同，可得出以下结论：

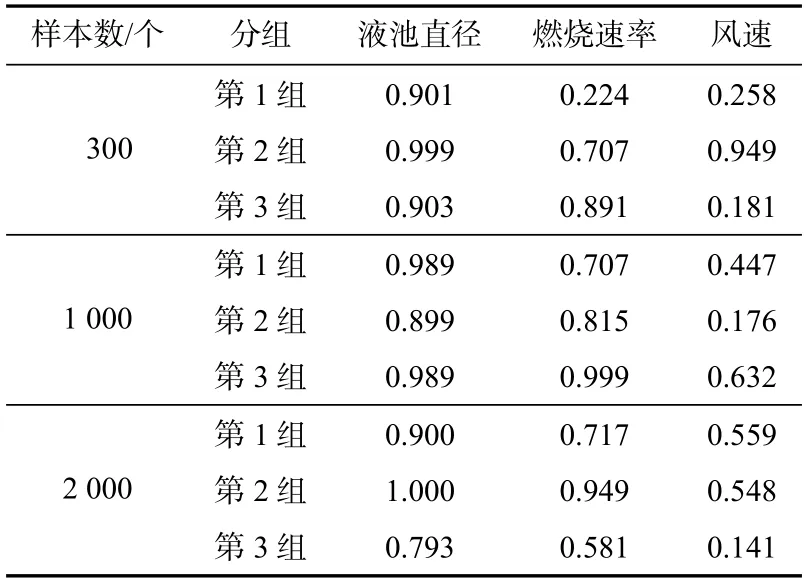
表2 Spearman 秩相关系数分析Tab.2 Spearman rank correlation coefficient analysis

（1）输油管道池火灾后果分析中3 个不确定性参数对热辐射强度的影响程度排序为：液池直径对池火热辐射通量的影响程度最大，其次是燃烧速率，风速对池火热辐射通量的影响相对较小。

（2）在不确定性参数概率分布和取值区间不变的情况下，样本量大于300 的计算结果能够满足后续池火灾事故后果的统计分析需求。

2.3 蒙特卡洛模拟及结果分析

2.3.1 池火灾热辐射通量分布

采用拉丁超立方抽样法对液池直径、风速和燃烧速率按其概率分布随机抽样30 组样本集，每组样本集由1 000 个组合样本组成，将样本数据代入池火模型进行30 000 次蒙特卡洛模拟，得到距事故点30 个不同位置处池火灾热辐射通量分布特征，这里取具有代表性的位置来分析热辐射通量的分布情况：距事故点10、15、20 和25 m 处池火灾热辐射通量分布情况如图5 所示。由图5 所得的热辐射通量分布可见，热辐射通量整体上随事故点距离的增大而减小。

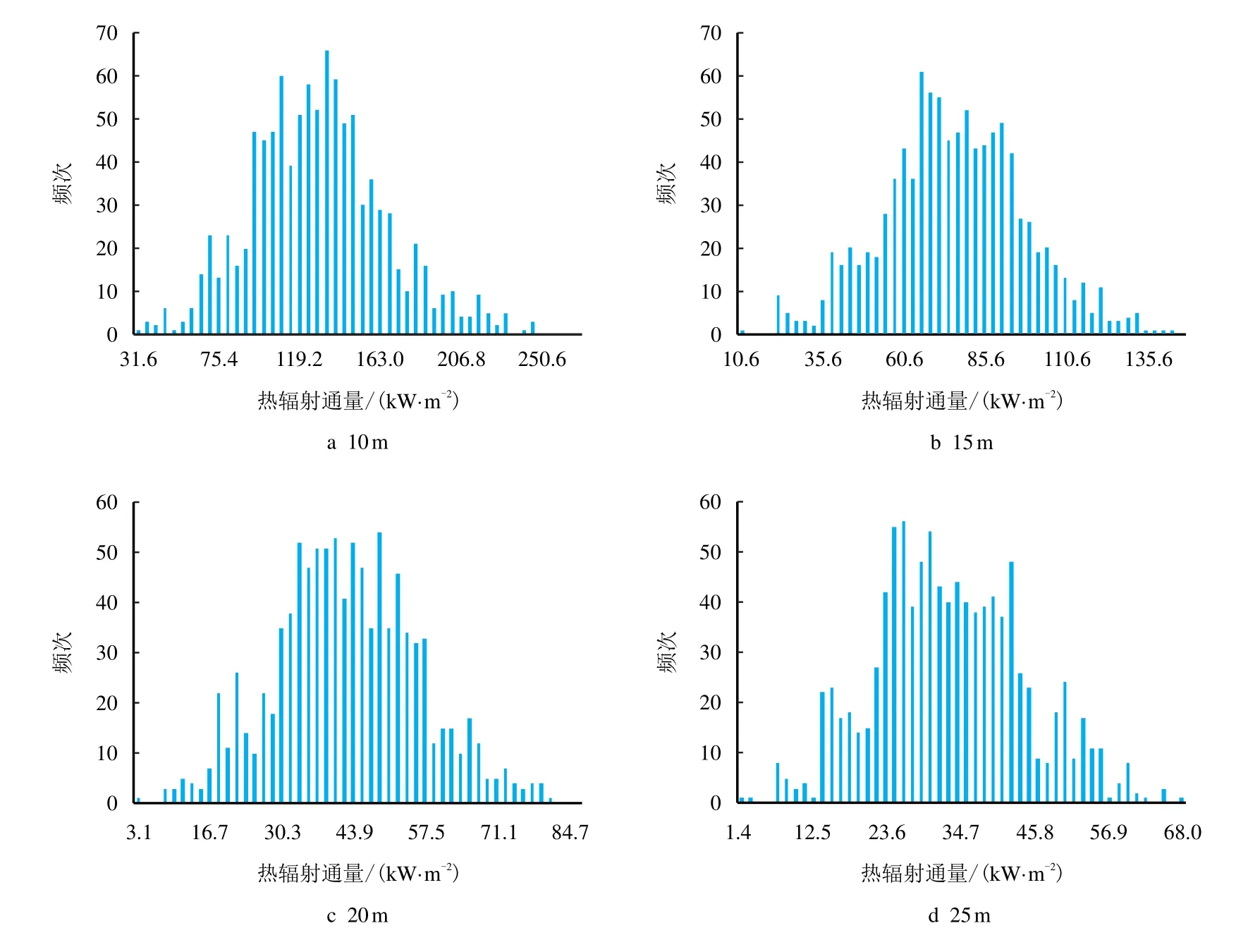
图5 距事故点不同位置处池火灾热辐射通量分布特征Fig.5 Distribution characteristics of heat radiation flux from pool fire at different locations from the accident point

2.3.2 池火灾事故后果分析

计算热辐射通量均值和致死率随事故点距离的变化规律见图6。其中，死亡的热辐射强度阈值的判断标准为35 kW/m2。

图6 热辐射通量均值及致死率与事故点距离的变化规律Fig.6 Variation of the mean heat radiation flux and fatality rate with the distance from the accident point

由图6 可见，随着事故点距离的增大，热辐射通量均值和致死率逐渐减小。实例中，致死范围对应的与事故点距离的变化范围为12～33 m；当距离小于12 m 时，致死率为100%；当距离大于33 m 时，致死率为0；致死率为50%时，距离为23 m。

3 结论

（1）采用拉丁超立方抽样法对液池直径、风速和燃烧速率3 个不确定性参数按其概率分布随机抽样30 组样本集进行蒙特卡洛模拟，结果表明，热辐射通量均值随距离的增大而减小。

（2）致死率分布统计学规律分析表明，致死率随距离的增大而减小，根据致死率概率分布确定的与事故点距离值可为管道周边风险区域等级划分提供依据。