力矩输出能力最优化混合执行机构操纵律设计

倪瑞，华冰，张宏，吴云华，陈志明

南京航空航天大学 航天学院，南京 211000

1 引言

航天器的敏捷机动控制与姿态动态跟踪控制，都需要执行机构输出大力矩以及具有较高的精确度[1]。执行机构有控制力矩陀螺[2-3]，飞轮[4]，磁力矩[5]等，单类的执行机构各有其局限性，传统的推力器精度低，CMG具有奇异问题[6]，RW具有饱和问题[7]等。因此，对于航天器的敏捷姿态控制，一般选用混合执行机构[8]，其中，CMG输出力矩线性度高，能够成倍的放大力矩而且响应迅速，但会有奇异的问题，RW虽然提供力矩较小，但控制精度高，可以和CMG协同使用，利用CMG对RW进行卸载，并利用RW使CMG逃离几何奇异。所以CMG和RW的混合执行机构由于其精度高、输出力矩大成为较好的选择[9]。

2013年，耿云海等提出了一种形式简洁的混合执行机构力矩分配算法[10]，避免了CMG奇异，避免了RW饱和和过零的问题，提高了精度。2015年，王焕杰等在CMG的基础上设计了RW的操纵律进行闭环修正，可以实现CMG在非奇异的状态下减小外界干扰等不利影响实现对大角度姿态机动的控制[11]。2017年，Yunhua Wu等提出了CMG和RW的新的性能指标，使用具有可行的零运动矢量梯度方法，使混合执行器系统达到可行状态，但并没有实现混合执行机构的性能最优化[12]。2019年，Yunhua Wu等提出了基于合作博弈的混合执行机构操纵律[13]，实现CMG角速度和RW角加速度的最小化，使得CMG和RW协同使用，并且使得能耗较小，但没有精确的衡量力矩输出的能力，2019年，张智飞等提出了CMG 系统零运动混合执行机构力矩分配方法[14]，采用高斯伪谱法进行了最优力矩分配，不仅避免了CMG奇异，而且缩短了敏捷卫星快速机动的时间。2020年，张科备等创新性的提出在构型上进行变化，使系统增加自由度[15]。以上方法或侧重于逃离奇异，而引入较大的力矩误差，或侧重于降低能耗，没有考虑在逃离奇异的前提下，力矩输出能力的最优化。

本文从几何角度出发，根据期望力矩与系统输出力矩的几何关系进行分析，使得期望力矩与输出力矩夹角最小。给出了力矩输出能力最优的CMG框架角速度和RW角加速度计算方法，设计了力矩输出能力最优化的混合执行机构操纵律，引入参数，使得CMG框架角和RW角加速度与期望力矩下的CMG框架角和RW角加速度的误差以及输出力矩误差的混合二次型最小，在避免CMG奇异和RW饱和的前提下，实现力矩输出能力强，精度高，可更好的完成航天器敏捷机动控制等任务。

2 混合执行机构的配置

2.1 金字塔构型的CMG和RW混合执行机构

混合执行机构采用金字塔构型，使用4个CMG和3个RW构成。4个CMG框架轴分别垂直于正四棱锥的4个侧面，与塔顶轴夹角均为β，初始角动量均沿正四棱锥的底边以逆时针顺序排列。3个RW正交分布。如图1所示。

图1 金字塔构型CMG和RW系统[16]Fig.1 Pyramidal CMG and RW system

CMG的框架角集合α=[α1,α2,α3,α4]T，倾角为β，CMG角动量hCMG为：

hCMG=

(1)

式中：c(β)≡cos (β) ,s(β)≡sin (β),s(αi)≡sin (αi),c(αi)≡cos (αi)，式(1)导数为：

式中：JCMG为CMG的雅克比矩阵；h0是标称角动量。

量的导数为：

混合执行机构的角动量导数为：

2.2 CMG奇异与RW饱和

CMG系统陷入奇异状态是指当CMG系统处于特定的框架角时，各个CMG输出的力矩共面，此时的CMG系统无法输出正交于该平面的力矩，该平面的法向量为奇异矢量，对应的 CMG 框架角为奇异框架角[17]。从数学推导的方面看，当CMG陷入奇异时，雅克比矩阵JCMG列向量不共面且互相平行，即不满秩：

采用CMG奇异度量函数SCMG来衡量CMG接近奇异的情况，SCMG越大，CMGs越远离奇异，当SCMG为0时，CMGs陷入奇异：

RW产生的力矩与加速度成比例，即RW的动量矩在某个方向上不断增大，直到飞轮转速达到极限值，这就意味着RW会陷入饱和，从而失去控制航天器姿态的能力，RW需要由其他辅助设备(例如推进器、磁力矩器等)进行卸载去饱和[18]。

类似于CMG的奇异度量函数，采用RW饱和指标SRW来衡量RW饱和情况，当SRW=1时，RW陷入饱和：

式中：Ωmax为饱和值。

CMG与RW互相耦合，当CMG奇异时，RW输出扭矩，使得混合执行机构逃离奇异。当CMG 奇异时，虽然rank(JCMG)=2，但混合执行机构：

所以，混合执行机构可以弥补单CMG作为执行机构容易陷入奇异的情况。

为体现力矩输出的精度，定义了力矩输出能力的性能指标[19]：

式中：θi为第i个CMG输出力矩τdi与期望力矩Tc之间的夹角，S越大输出能力越强，S=0表示无法输出期望力矩。

3 力矩输出最优化原理

根据期望力矩矢量及CMG力矩输出的几何关系，来使得输出力矩与期望力矩之间的夹角最小，实现力矩输出能力最优。所以，本文从几何角度出发，合理分配各个CMG的框架角，设计了力矩输出最优化原理，使得力矩输出能力最强，最优化框架角速度的设定如图2所示[19]。

图2 最优化框架角速度的设定[19]Fig.2 Setting of optimal frame angular velocity

sgn(〈hi×hdi,hi〉)

为使得输出能力最优，经过一个控制周期Δt之后，当前框架角应与期望的框架角重合，则期望的框架角速度为：

则各个CMG的期望框架角速度为：

由于RW可以提供各个方向的力矩，为使得CMG和RW互相耦合，则使得RW的期望的角加速度如下：

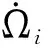
使得CMG和RW协同使用，RW的角速度受到CMG的控制，当CMG出现奇异情况时候，RW起作用，给予小力矩使得CMG更容易逃离奇异状态，使整个系统迅速逃离奇异，能继续执行任务[12]。

4 执行机构的操纵律设计

基于力矩输出能力最优化的混合执行机构操纵律在精准的输出期望力矩的同时保证力矩输出能力最大。本文给出力矩期望最优的CMG框架角与RW角加速度，引入混合最小二次型，使得CMG框架角和RW角加速度与期望力矩下的CMG框架角和RW角加速度的误差以及输出力矩误差的混合二次型最小，即保证角速度误差与力矩输出误差同时最小，引入了参数，使得操纵律一直存在力矩误差，并通过减小参数，一定程度上降低在奇异面产生的力矩误差。

其中，混合最小二次型L[19]：

(2)

其中L取最小值且矩阵A，B取为单位对称矩阵。

(3)

取B=E3，A=λE7。其中Ei(i=3,7)为单位矩阵，λ为减小力矩误差的参数，代入(3)得到：

(4)

根据Woodbury公式，变换(4)为[10]：

式中：λ=λ0exp(μSCMG)。

5 力矩误差与奇异性分析

5.1 力矩误差分析

得到矩阵为：

式中：B=E3，A=λE7。

混合执行机构的期望力矩为：

输出力矩误差为：

式中：A+DTBD=λE7+DTD由于λ≠0，所以不可逆，则输出力矩误差不为0，使得操纵律总是存在一定的力矩误差。降低λ的取值，减小力矩误差。取λ=λ0exp(μSCMG)，当在CMG奇异点附近，SCMG→0,det(DTD)→0,λ迅速减小，ΔT→0。 同时，λ≠0将使得操纵律总是存在一定的力矩误差，降低λ的取值，减小力矩误差。

对于λ=λ0exp(μSCMG)，取当SCMG=0.04时，针对λ0的值进行讨论，如图3为误差参数对三轴力矩误差的绝对值和的影响，当λ0减小，即为λ的减小，可以显著减小系统的力矩误差和，但是，当λ0小于1×10-3后，减小效果不显著。

图3 参数λ对力矩误差和影响Fig.3 Effect of parameter λ on sum of torque error

如表1为，考虑λ0对框架角速度误差和的影响。

表1 参数λ0对框架角速度误差影响

可见，框架角误差越大，框架角速度误差和越大，而λ0→0，框架角速度误差和变化越大，即系统对框架角的误差的处理能力越来越差。

所以针对上述情况，取λ0=0.000 1，在减小力矩误差的同时误差处理能力也较好。

5.2 CMG奇异性分析

对基于力矩输出能力最优化的混合执行机构操纵律中CMG奇异逃离进行证明，并分析混合执行机构与单CMG系统的不同。证明基于力矩输出能力最优化的混合执行机构操纵律逃离CMG的奇异效果更好。

(5)

代入(5)可得：

可得：

CMG奇异情况可以分为以下三种情况：

Case1：雅可比矩阵第一行为0，c(α1,k)=s(α2,k)=c(α3,k)=s(α4,k)=0,

Case2：雅可比矩阵第二行为0，s(α1,k)=c(α2,k)=s(α3,k)=c(α4,k)=0,

Case3：雅可比矩阵第三行为0，c(α1,k)=c(α2,k)=c(α3,k)=c(α4,k)=0,

当没有RW时，

(6)

令B=

代入(6)得：

则可得：

(7)

6 仿真结果与分析

6.1 混合执行机构仿真参数设置

在本节中，对基于力矩输出能力最优化的混合执行机构操纵律进行仿真分析，混合执行机构的参数设定如表2所示。

表2 混合执行机构参数

本节考虑4个方案，如表3所示。其中方案1和2采用混合执行机构的最优化操纵律，但分别采用不同的期望力矩作为对比，分别为低动态性的期望力矩以及高动态性的期望力矩。方案3是当混合执行机构一开始便陷入奇异的极限状态，基于力矩输出能力最优化的混合执行机构操纵律逃离奇异的能力。方案4为基于合作博弈的混合执行机构操纵律[4]，考虑与方案3同样的极限状态下，逃离奇异情况，作为与方案3的对比方案。

表3 仿真方案设计

6.2 仿真分析

图4 方案1仿真结果Fig.4 Simulation results of scenario 1

图5 方案2仿真结果Fig.5 Simulation results of scenario 2

如图6，为系统初始框架角双曲线奇异情况，可见，图6(a)，CMG奇异性指标在0s为0，即初始奇异，但随着时间流逝，立刻逃离奇异，且不会再陷入奇异状态，RW饱和指标未达到1，即RW不饱和，同时(c)可见，力矩误差较小，输出力矩接近于期望力矩，(d)可见，混合执行机构力矩输出能力较强。

图6 方案3仿真结果Fig.6 Simulation results of scenario 3

续图6Fig.6 Continued

如图7，为基于合作博弈的混合执行机构操纵律下系统初始框架角双曲线奇异情况，图7(a)，CMG奇异性指标在0 s为0，即初始奇异，但随着时间流逝，立刻逃离奇异，图7(b)RW饱和指标未达到1，即RW不饱和，图7(c)可见，力矩误差较小，与图6类似，但从图6(d)和图7(d)对比可以看出合作博弈的混合执行机构操纵律的S较小，所以针对力矩输出能力而言，合作博弈的混合执行机构操纵律力矩输出能力较差。

图7 方案4仿真结果Fig.7 Simulation results of scenario 4

根据表4，得到以下结论：

1)对于混合执行机构，当初始CMG不奇异时，由于期望力矩会导致CMG接近奇异状态，基于力矩输出能力最优化的混合执行机构操纵律使得系统很快逃离奇异，且输出力矩误差较小，力矩输出能力强；

2)对于混合执行机构，当初始CMG陷入奇异时，对于这种极限状态，例如双曲线奇异，基于力矩输出能力最优化的混合执行机构操纵律可使系统迅速逃离奇异，并在下次接近奇异的时候使系统远离奇异，且输出力矩误差较小，力矩输出能力强；

表4 仿真效果分析

3)与现有的逃离奇异效果较好的，基于合作博弈的混合执行机构操纵律的输出能力进行对比，可见，力矩输出能力最优化混合执行机构操纵律的力矩输出能力较强。

7 结论

本文采用CMG和RW的混合执行机构，设计了基于力矩输出能力最优化混合执行机构操纵律，引入了λ参数，使得操纵律一直存在力矩误差，通过对λ参数对力矩误差和的影响和λ参数对框架角的误差的处理能力的影响，选取了最优情况下的λ参数，使之在一定程度上降低系统奇异面上产生的力矩误差。证明了基于力矩输出能力最优化的混合执行机构操纵律中CMG奇异逃离较好，并分析了基于力矩输出能力最优化混合执行机构操纵律比基于合作博弈的混合执行机构操纵律输出力矩能力更强。经过仿真验证，基于力矩输出能力最优化的混合执行机构操纵律的CMG逃离奇异能力较好，并且RW不会陷入饱和，只会引入很小的力矩误差，力矩输出误差小，并且力矩输出能力强。适用于航天器的高动态敏捷机动或者姿态动态跟踪控制等任务。