星间相位干涉仪测角系统设计及精度分析
朱粮伟,李明成,王春晖,金仲和
浙江大学 航空航天学院,杭州 310027
1 引言
微小卫星编队飞行、多星协同作业可以实现传统单颗大卫星无法实现的功能。比如,能够在同一时刻对同一目标实现多维度探测,能够提供大孔径和长测量基线,对通信、导航、遥感、电子侦察、精确定位、大气人文和地球物理观测等诸多领域具有非常重要的意义。高精度星间相对状态测量技术是多星协同作业的关键技术之一,其中包括测距、测角、测速技术,是卫星编队执行更加精细的太空任务的重要基础。
传统的星间相对测量方法有激光测量[1]、红外测量[2]、可见光视觉测量[3]、GPS相对测量[4]等,但各自存在测量波束窄、易受空间辐射和强光影响、依赖近地轨道的GPS信号等缺点,而本文使用的无线电测量法不依赖于外界信号和轨道高度。本文的研究重点是星间相对角度测量系统,早期的无线电测角系统主要有幅度比较式测角[5]、多普勒测角[6]、到达时间差测角等。近年来,空间谱估计[7]和干涉仪技术是无线电测角的研究重点。干涉仪测角技术又分为相关干涉仪[8]和相位干涉仪,本文使用的相位干涉仪方法具有测角速度快、计算复杂度低的优势。
基于目前的研究现状和浙江大学微小卫星研究中心某卫星研制任务的需求,将相位干涉仪技术应用于微小卫星星间测量系统,提出的系统在非相干伪码测距的基础上,利用测距系统的已有数据,使用相位干涉法结合载波相位测量值实现星间角度的测量。
本文的系统设计和精度分析有较强的通用性,对于有类似结构的卫星扩频接收机可以采用此方案扩展通道实现角度测量,且噪声源的传递过程基本相同,所以对于星间测距系统、卫星通信接收机等的功能扩展和精度分析有借鉴意义。
2 系统设计
在类GPS接收机的硬件基础上提出了一种星间相位干涉仪测角系统,系统结构如图1所示。

图1 星间相位干涉仪测角系统结构Fig.1 Structure of inter-satellite phase interferometer angle measurement system
图1中的系统结构包含三条相同的接收机通道,单个通道的设计采用已经较为成熟的超外差式接收机结构,天线接收到的信号经过馈线传输到射频前端进行放大和滤波,下混频获得的中频信号通过ADC采样后送入FPGA中的基带信号处理单元进行处理。单个通道的基带信号处理算法是已经有较多应用的非相干扩频测量法,使用载波跟踪环路(Costas环)获得多普勒频移和载波相位测量值,使用伪码的延迟锁定环路(delay lock loop,DLL)获得码相位和伪距测量值[9]。测角系统在单通道测距系统的基础上增加了两条通道,可以利用通道已有信息,在不增加额外硬件开销的情况下,通过相位干涉法比相后得到星间相对角度(方位角、俯仰角)。此方法利用信号到达各通道天线的距离不同而产生相位差异,根据几何关系计算出信号的来波方向。星间相对状态解算单元通过主测量通道的伪码相位解算出星间相对距离,通过主测量通道与其他两路测量通道载波相位测量值比相得到星间角度。
这种星间测角系统结构简单,且与测距系统融合,数据处理方式简单,不需要完成复杂的后处理和估计运算,所以测量值实时性好,且可以得到高精度的测量值。
在图1中的每条接收通道上,在不同信号处理环节中都会受到各种噪声的影响,如热噪声、本振系统相位噪声等。如果噪声过大,就会影响测量系统的信号质量,进而造成测量值的恶化,因此对不同种类噪声理论建模与分析具有重要的意义。
3 噪声模型及其传递函数
3.1 单通道噪声源分析
在噪声模型分析中,一般都认为噪声以加性噪声的方式造成信号的信噪比恶化,从而影响测量精度。首先给出载波信号信噪比SNR的定义[10]:
(1)
式中:C为载波功率;N0为噪声功率谱密度;BL为接收机带宽。
则载波相位测量值误差σφ与信噪比SNR有以下关系式
(2)
单通道接收机系统主要的噪声源有以下几种。
1)热噪声。常温下热噪声功率谱密度为-174 dBm/Hz[11]。假设输入信号功率大小为S,系统噪声系数为Nr,则进入载波跟踪环路的噪声功率谱密度(dBc/Hz)为
Stemp(f)=-174-S+Nr
(3)
对于热噪声而言,由式(3)可知,可以通过减小接收机带宽来有效降低热噪声产生的误差。
2)本振系统相位噪声。测量系统的本振系统由晶体振荡器和锁相环构成,晶体振荡器作为系统的参考频率源,锁相环用于输出系统所需的载波信号。相位噪声的功率和距离载波的频偏成反比,详细模型较为复杂,本文使用1/f噪声来近似写为[12]
(4)
式中:fref为参考频率;Nref为在参考频率点的相位噪声功率大小。
3)量化噪声。ADC是接收通道中的关键器件之一,ADC的量化噪声和孔径抖动是影响信号测量精度的重要因素[13]。其中量化噪声的功率谱密度为
(5)
式中:fs为抽样频率;σe2为量化噪声总功率,一般表示为
(6)
式中:Δ=2-N,N为ADC位数。
以dBc/Hz为单位的量化噪声功率谱密度可以改写为
(7)

4)孔径抖动噪声。ADC在采样保持的过程中存在开关时间的不确定性和采样时钟的相位噪声,这会引起孔径抖动,其噪声功率谱密度为[14]
(8)
式中:f为信号频率;tjitter为孔径抖动时间。
除此以外,整个测量系统中还存在多径噪声、电源噪声和其他器件自身噪声[15],但对测角系统精度影响较小,本文中不再考虑。
3.2 多通道噪声传递分析
测角系统中的各类噪声经过系统环路的传递,最终会成为DLL环与Costas环输出信号的噪声,所以噪声对测量结果的恶化不仅与噪声功率水平有关,还与其经过系统的传递函数有关。此系统本质上是对相位差进行测量,因此在传递过程中不考虑幅度的影响,只对相位的时域和频域进行分析。测量系统的噪声传递关系如图2所示(以其中两条通道比相为例)。
图中各个符号表示的含义是:IF为发射端中频信号,SLO1(f)为发射端的本振相位噪声;τ1与τ2分别为发射天线到接收通道1与接收通道2各自天线的传播延时;Stemp1(f)和Stemp2(f)为两条通道各自的热噪声;τ3与τ4为通道1与通道2下混频前的路径延时;SLO2(f)为接收端的本振相位噪声;Squanti1(f)和Squanti2(f)分别为通道1与通道2的量化噪声;Sjitter1(f)和Sjitter2(f)分别为通道1与通道2的孔径抖动噪声;τ5与τ6为通道1与通道2混频后到环路前的路径延时;φ1和φ2为通道1与通道2的载波相位测量值。

图2 系统噪声源分布和传递关系Fig.2 The distribution and transfer relationship of noise sources in this system
从图2的噪声传递关系中,可以得到各个噪声源到比相器输出结果的传递函数如表1所示。

表1 噪声源对应的传递函数
上表中:Δτ=(τ1+τ3+τ5)-(τ2+τ4+τ6),为两个通道信号传播路径总延时差;τtol=τ1+τ2+τ3+τ4+τ5+τ6,为两个通道信号的传播延时总和;H(f)为载波环的系统传递函数,可以表示为[16]
(9)
式中:K1与K2为环路设计参数,α一般考虑为1。实际上,Costas环是在FPGA内部实现的数字环路,当环路更新速率足够快时,数字环路的性能等价于模拟环路,所以可用模拟环路的方法来分析。Costas环路具有低通特性,可以滤除高频信号成分和噪声。K1和K2的设计一般根据环路的等效噪声带宽2BL和阻尼系数ζ来计算,它们之间的关系为[16]
(10)
(11)
工程中,2BL的选取根据系统动态特性来确定,ζ的取值范围在0.5~2之间。本系统中,ζ取1,2BL取3 kHz。
另外,根据表1中的传递函数,本振相位噪声的传递函数除了与Costas环路的传递函数有关,还与通道间的路径延时差有关。下面分段分析图2中传输路径上的延时大小和两通道间的延时差大小,同时对系统采用的平衡通道一致性的方法进行介绍。
τ1和τ2表示发射端到通道1和通道2的空间传输延时,当星间最大相对距离为30 km时,该传输延时不大于10 ms。令Δτ1=|τ1-τ2|,有
(12)
式中:D为两个通道接收天线基线长度;θ为两星相对角度;c为光速。本系统中天线基线长度D=1 m,两星相对角度范围为±60°,可得Δτ1≤2.9 ns。
τ3和τ4表示发射端到接收天线、混频器前的传输延时,经过的器件主要有天线、天线馈线、滤波器、低噪放和各器件之间的传输线,该路径中各器件对信号的群延时均为纳秒级,通过仪器可以测得τ3和τ4大约为150 ns。令Δτ2=|τ3-τ4|,主要由不同天线相位中心的不一致性引起,相位中心偏差一般为几个毫米[17]。本系统使用同型号同批次的天线,这将造成两通道间0.02~0.08 ns的延时差,路径中的其他器件的不一致性较好,所以一般可以认为Δτ2≤1 ns。
τ5和τ6表示混频器到ADC的传输延时,经过的器件主要有混频器、中频滤波器、中频放大器和各器件之间的传输线。在本系统中,该段路径由集成单芯片LMS7002实现,具有较小的传播延时,τ5和τ6大约为50 ns。令Δτ3=|τ5-τ6|,单芯片内部集成了两个接收通道,两通道具有完全相同的设计,一致性良好,所以一般可以认为Δτ3≤1 ns。
根据各段路径的延时,可以得到发射端和接收端的本振相位噪声功率谱传输函数,分别记为|G(f)|2和|W(f)|2,如图3、图4所示。

图3 发射端本振相位噪声功率谱传输函数Fig.3 Power spectrum transfer function of the local oscillator phase noise at the transmitter

图4 接收端本振相位噪声功率谱传输函数Fig.4 Power spectrum transfer function of the phase noise of the local oscillator at the receiver
图3显示了系统对于发射端本振相位噪声有优于90 dB的抑制作用,而且该抑制作用随着信号在两通道之间的传播延时差的减小而增强。由于Δτ3较小,所以图4中系统对于接收端本振相位噪声有优于105 dB的抑制作用。
可见,将通道间延时差尽可能降低是多通道比相测角系统必须重视的问题。考虑到这种延时差主要由器件的不一致性引起,包括天线、放大器、滤波器、混频器以及电阻、电容和电感等,实际系统设计时做了大量的一致性设计。
使用相同器件和PCB布局在接收机单板上集成了两个测量模块,单个模块包括两个测量通道,共四个通道经过两两比相得到两个角度值。单个测量模块的两个通道信号使用同一片FPGA进行处理,这两个通道连接到单芯片LMS7002内部的两个接收通道进行一致性优越的混频、滤波和模数转换,比相时将会大大消除系统噪声。并且两个测量模块的FPGA使用同一个频率源,可以消除大部分相位噪声。
4 仿真计算
4.1 噪声功率的仿真计算
通过上一节对各个噪声源模型及其传递函数的分析,可以计算噪声经过系统传递后的功率大小,从而分析影响测角精度的主要和次要的噪声源。
当系统输入信号功率为-80 dBm且接收机噪声系数为4 dB时,热噪声功率谱密度为-90 dBc/Hz,通过链路的传递,比相器输出端的噪声功率谱密度为
Ntemp=Stemp1+10log10|H(f)|2+
Stemp2+10log10|-H(f)|2=
-87+10log10|H(f)|2
(13)
本振系统的相位噪声在频偏为10 kHz处的大小为-92 dBc/Hz,首先计算发送端的本振相位噪声传递到比相器输出端的噪声功率谱密度为
NLO1=SLO1+10log10·
|2H(f)sin (πfΔτ)e-jπfτtol|2=
|2H(f)sin(πfΔτ)e-jπfτtol|2
(14)
同样,接收端的相位噪声传递到比相器输出端的噪声功率为
NLO2=SLO2+10log10·
|2H(f)sin[πf(τ5-τ6)]e-jπf(τ5+τ6)|2=
10log10|2H(f)sin[πf(τ5-τ6)]e-jπf(τ5+τ6)|2
(15)
本系统中使用的ADC为10位,采样带宽为20 MHz,计算得到量化噪声功率谱密度为-135 dBc/Hz,传递到比相器输出端的噪声功率为
Nquanti=-135+10log10|H(f)|2-135+
10log10|-H(f)|2=-132+10log10|H(f)|2
(16)
系统中的中频频率为10 MHz,孔径抖动时间约为3.56 ps,可以计算出孔径抖动噪声功率谱密度为-146 dBc/Hz,传递到比相器输出端的噪声功率为
Njitter=-146+10log10|H(f)|2-146+
10log10|-H(f)|2=-143+10log10|H(f)|2
(17)
至此,可得各噪声经过传递后的功率谱密度如图5所示,其中横坐标f表示频率点,纵坐标S(f)表示功率水平。
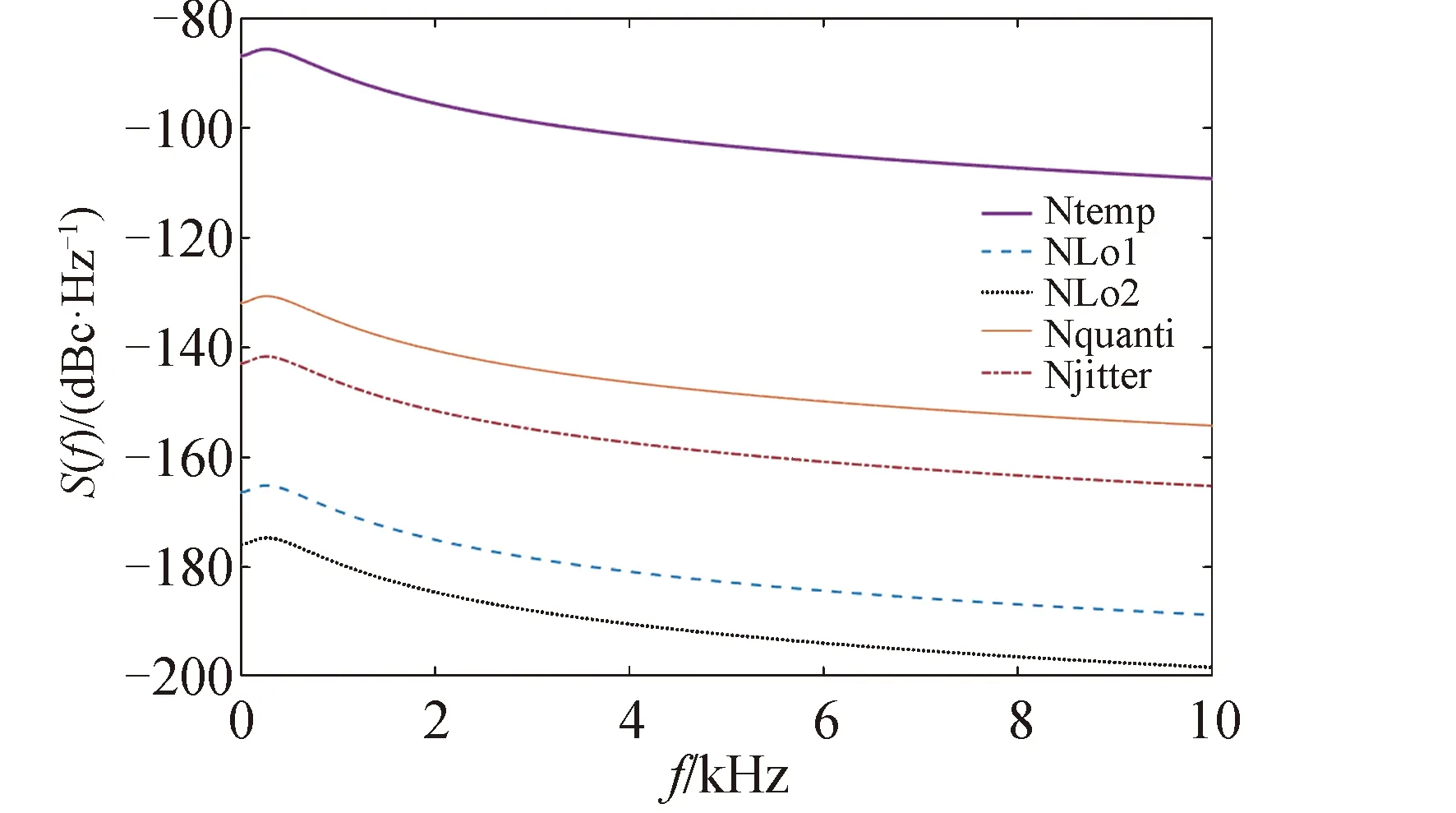
图5 噪声源经过传递后的功率谱密度曲线Fig.5 The power spectral density curve of the noise source after transmission
系统中影响最大的噪声源为热噪声,功率水平在-90 dBc/Hz左右,其次是量化噪声和孔径抖动噪声,功率水平都在-140 dBc/Hz左右,本振相位噪声在测角系统中被抑制到-160 dBc/Hz以下,不再是主要的噪声源。
4.2 角度测量误差的仿真计算
利用测角系统的比相器输出端噪声功率计算相位差Δφ的误差为
(18)
式中:L(f)是以dBc/Hz为单位的噪声功率谱密度;BL为接收机带宽。相位差Δφ和待测角度的转换公式为
(19)
式中:θ为系统测量角度;λ为载波信号波长。
需要注意的是,在利用式(19)将载波相位差转换为角度时,必须保证进行比相的载波相位值已经被正确地解模糊。本系统使用一种利用伪距来确定模糊度的简单方法,伪距ρ与载波相位φ有如下关系
ρ=λ(φ-Nc)
(20)
式中:Nc为整周模糊度。为了使Nc的估计值误差小于1周,系统的伪距测量误差需要小于载波波长。
式(20)的解模糊过程对伪距测量精度提出了要求,单通道伪距解算的关键是利用接收机码跟踪环路提取码相位,本系统使用的DLL环路已有较多研究。因为载波相位测量值比伪距测量值要精确、平滑得多,所以使用了载波相位平滑伪距的方法,将两种测量值加权整合得到一种相对平滑、误差更小的伪距,以达到进一步提高精度的作用[18]。
在现有的扩频技术发展水平下,本系统选择码速率为10.23 M码片/s、码长1 023的伪随机码,测量信号选用S波段,载波波长0.133 m,在星间动态性不大的场景下,可以达到厘米级的距离测量精度[19],可以满足利用伪码解算载波整周模糊度的要求。
在接收机信号输入功率较强(以-80 dBm为例)、环路参数和通道一致性如3.2节所设计并且载波相位测量值被正确解模糊的前提下,可以计算各噪声源引起的测角误差的量级大小如表2所示。

表2 各噪声引起的测角误差量级
可以认为系统中各误差项相互独立,综合考虑各误差项得到系统角度测量误差为
1.14×10-4
(21)
另外,再次分析通道间不平衡性导致的测量偏差,引起此偏差的原因主要是天线相位中心偏差、射频连接线缆的不同弯曲程度等。这将造成传播延时不完全相同,也就是Δτ2+Δτ3≠0,图6中给出了通道间延时差与测角误差的关系,其中横坐标t表示延时差,纵坐标Δθ表示角度测量误差。可见纳秒量级的通道间延时差会对角度测量结果产生巨大的影响,0.5 ns的延时差会使测量角度偏差约10°。当延时偏差超过2.6 ns时,带来的测量结果偏差将超过系统的角度测量范围±60°,产生系统错误。但是,通道间延时偏差属于稳态误差,可以通过系统校准消除其对测量结果的影响[20]。

图6 通道间延时差与测角误差的关系曲线Fig.6 The relationship curve between the delay difference among channels and the angle measurement error
5 试验验证
如图7所示,星间角度测量系统至少由两颗卫星组成,一颗为主星,为状态解算方,主星上的一个单机由一路发射链路和两路接收链路组成,另一颗为从星,使用一路发射链路和一路接收链路。实验平台中主星发射端经过可调衰减器和射频线缆接入从星接收端,从星发射端经过可调衰减器接入一个3 dB功分器分为两路后再接入主星接收端的两个接收通道。每条发射链路的硬件组成主要包括射频滤波器、低噪声放大器和功率放大器,每条接收链路的硬件组成主要包括射频滤波器和低噪声放大器。其中集成单芯片LMS7002集成了信号放大、滤波、混频、增益控制和ADC/DAC等功能,系统使用Xilinx Spartan6 FPGA完成基带数字信号处理部分,通过串口向PC输出两条接收通道上的载波相位测量值,即可完成相对角度测量。
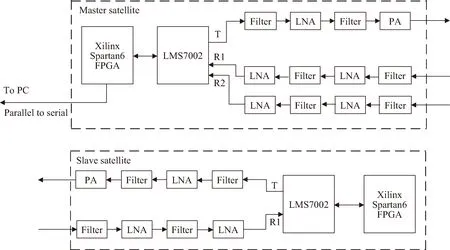
图7 系统硬件链路组成Fig.7 Block diagram of the hardware system
由于不同的输入信噪比将会影响最后的测量精度,在测试时用可调衰减器改变输入信号功率,使输入主星接收端的信号功率从-110 dBm开始增加至-50 dBm,每个功率下连续测试30 min,每阶段增加10 dB功率。在PC端计算得到7种输入功率下的测角值,将其中180 s的连续角度测量值表示在图8中。

图8 不同输入功率下,180 s内的连续角度测量值Fig.8 Continuous angle measurement value for 180 s under different input power
计算每种输入功率下测得的角度测量值的标准差,并且用式(21)计算得到该输入功率下综合考虑各误差项后的系统角度测量误差理论值,结果如图9所示,其中横坐标P表示输入信号功率,纵坐标Δθ表示角度测量误差。需要说明的是,本系统在试验中使用一段时间内的测量值标准差表示测量精度,实际的真实测量值可以通过角度测量零值标定试验来确定,在研究系统测量精度的试验中不予考虑。

图9 不同输入功率下系统角度测量误差理论值与实测值变化Fig.9 Theoretical value and actual measured value of angle measurement error under different input power
当信号输入功率从-110 dBm增加到-70 dBm时,角度测量精度随之增加,试验得到的测角精度变化趋势与图9中理论精度变化趋势相同,当输入功率为-80 dBm时,根据试验数据得到测角精度为1.4×10-3度,前文已经计算出此输入功率下的理论测量精度为1.14×10-4度,理论测角精度高于实测值。这是因为系统中存在多种噪声,且理论分析得出热噪声是最主要的噪声,热噪声造成的测角误差随载噪比的增加而减小,但是在实际测试系统中也会存在尚未考虑到的噪声源,导致实测值与理论值有一定的偏差。另外,当输入功率增加到-70 dBm后,如果再进一步增大输入功率,测角精度不再明显增加。这主要是因为误差来源中只有一部分是由热噪声引起的,测角精度也会受到如本振相位噪声、ADC量化误差、电源工频干扰等其他噪声源的影响,导致测量误差不完全跟随输入信噪比变化。
根据本系统的噪声特性,热噪声是主要的噪声源,所以减小接收机噪声带宽可以有效减小噪声水平,提高测量精度。另外,测量通道间不一致性导致的延时差对角度测量精度有很大影响,可以通过添加校准信号源来标定路径上的延时差,通过标定不同通道天线、不同来波方向的天线相位中心偏差,从而消除这种系统误差。
6 结论
本文提出了一种高精度的星间相位干涉仪测角系统,系统在已有较多应用的单通道伪码测距系统的基础上增加两条通道,利用已有的测量值,可以得到高精度的星间角度,后续数据处理后可实现星间相对定位。本文对该测角系统信号传输链路上的噪声模型及其传递函数进行了推导,仿真计算了不同噪声的噪声水平和对测角精度的影响量级。结果表明系统对本振相位噪声有90 dB以上的抑制作用,热噪声是角度测量的最大噪声源。通过实际测试,得到了角度测量精度随输入信号功率的变化关系,当信号输入功率从低水平增加时,测角精度随之增加,当输入功率增加到一定程度后,测角精度不再明显增加。试验数据表明,系统角度测量精度在强信号下可达1.4×10-3度。
根据研究成果,可以为类似的卫星扩频接收机在不改动过多方案的情况下实现星间测角功能提供参考,为搭建的这类测量系统的精度分析提供可通用的噪声传递函数,对其进行方便的理论分析。
本文明确了限制星间测角系统精度的主要因素,对后续系统优化和扩大应用范围起到了指导作用。进一步的研究工作将是针对提出的噪声源进行优化,对通道间不一致性这一系统差进行校准也是实际系统中的重要问题。

