天基星空背景观测覆盖范围计算方法研究
孙杨雨茜,乔栋,张晨,朱政帆,温昶煊,*
1. 北京理工大学 宇航学院,北京 100081 2. 中国科学院 空间应用工程与技术中心,北京 100094 3. 航天东方红卫星有限公司,北京 100094
1 引言
近年来,人类持续的太空活动导致空间碎片数量急剧攀升,空间环境日趋复杂。针对空间碎片这类大规模微小目标,传统地基观测由于受到大气环境干扰和探测目标尺寸限制任务所需成本较高。相对地基观测,天基观测不受大气影响,在监测暗弱目标时具有独特的优势,可作为传统地基观测的有效补充。
遥感卫星的观测覆盖问题包括两类:①对地观测覆盖问题,也称之为“地球背景观测”(Below-The-Horizon,BTH);②对空间目标的观测覆盖问题。由于地球的热背景干扰会使卫星对空间目标的探测失效,因此第二类问题也被称为“星空背景观测”(above-the-horizon,ATH)问题。
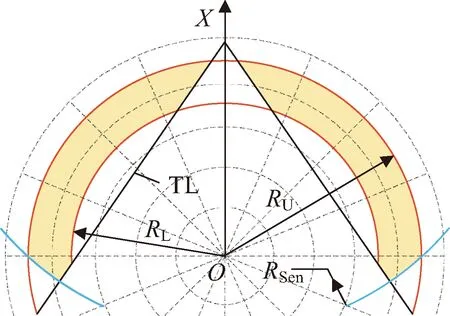
需要注意的是区分BTH和ATH的边界(horizon)并不是真正的地球几何形状边界,而是基于大气影响考虑的一个地球同心球面(tangent height shell,THS)[1],如图1所示。BTH和ATH问题可以通过一个切线高度圆锥(tangent height cone,THC)来界定,该圆锥由无数条从卫星出发与THS相切的切线(tangent line,TL)构成。为更好地说明两类覆盖情况关系,图1给出了由TL划分的ATH与BTH区域示意,TL以上为ATH区域,TL以下为BTH区域。当前,以全球连续覆盖[2-7]或特定目标区域覆盖[8-12]的星座设计为代表的BTH问题研究已经较为完善,而针对ATH问题的研究较少,尤其是复杂约束下的覆盖问题仍待解决,有必要开展更为深入的研究。
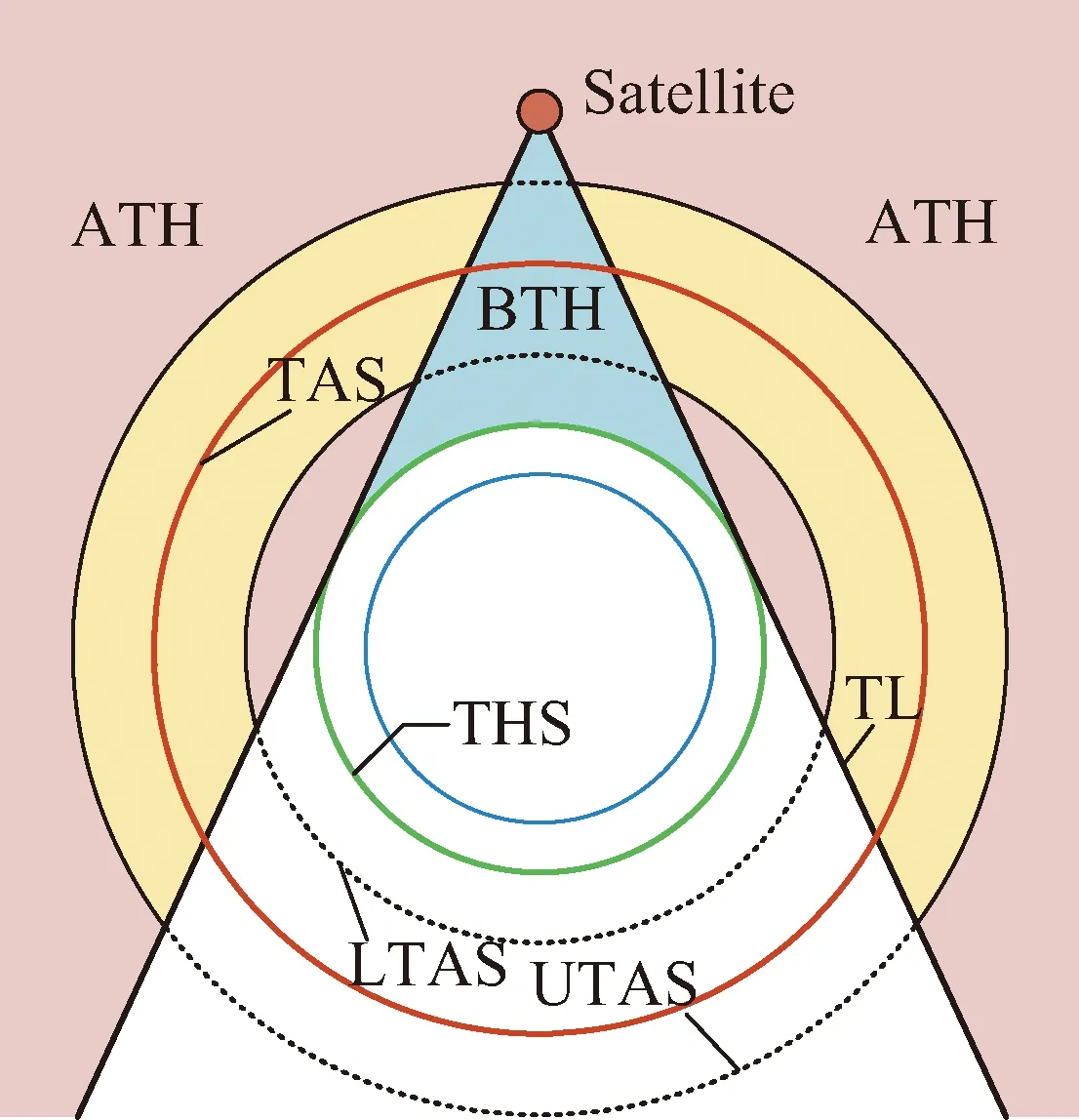
图1 ATH与BTH覆盖示意Fig.1 Diagram of ATH and BTH coverage
ATH问题可分为如下几类不同的覆盖情况。
单高度面覆盖:研究对象为图1中红色实线所示目标球面(target altitude shell,TAS),研究内容具体分为一维覆盖弧角和二维空间覆盖球面两类。
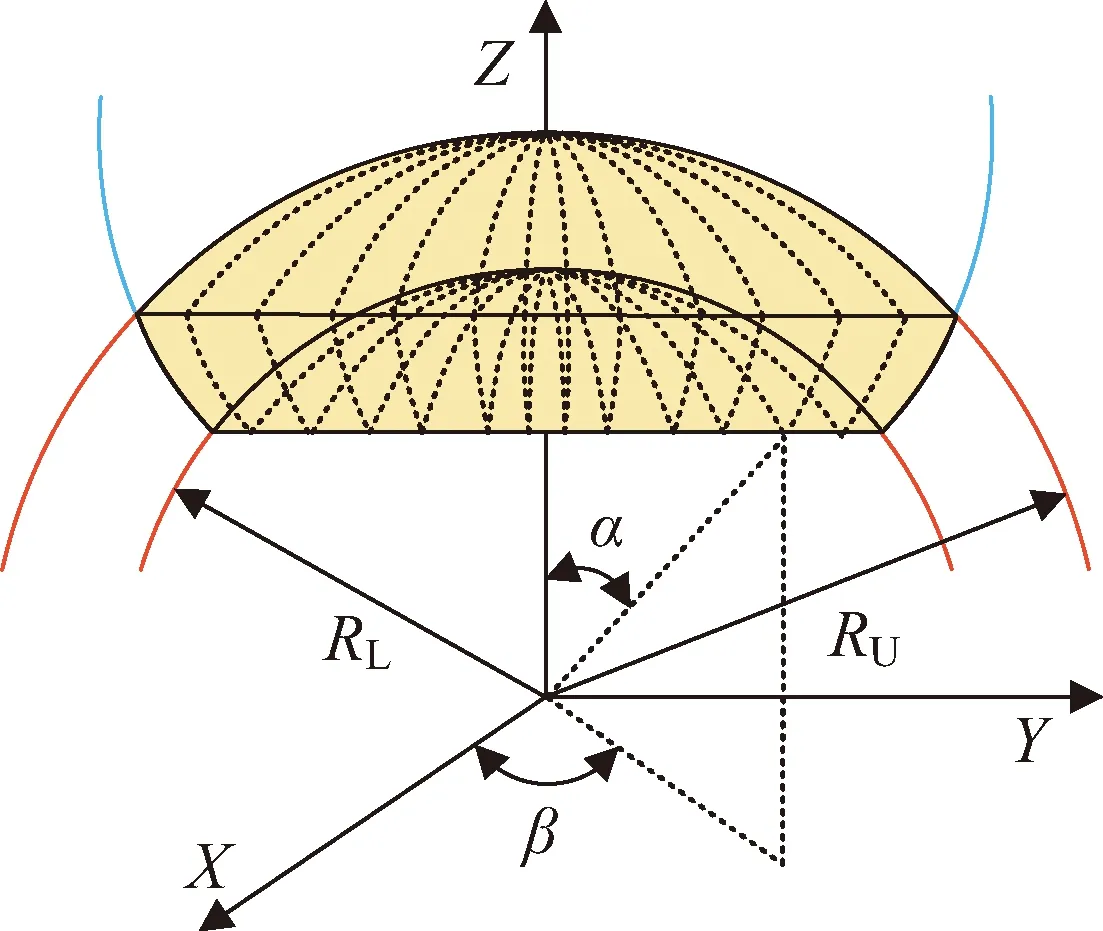
双高度段覆盖:研究由目标高度下限(lower TAS,LTAS)和目标高度上限(upper TAS,UTAS)决定的三维目标球层,如图1中黄色区域所示。研究内容具体分为二维平面覆盖面积和三维空间覆盖体积两类。
此外,根据是否考虑传感器有效范围约束,ATH问题又可划分为“无限传感器范围”和“有限传感器范围”两类。
早期ATH研究主要考虑无限传感器范围的情况。文献[13-14]研究了空间ATH覆盖问题。但在对地指向大视场角或位于高轨道的无限传感器设定下,极限覆盖情况一定出现在LTAS处。因此该阶段研究实际只针对LTAS单高度面展开,并等效于三维空间覆盖情况。之后,文献[15]在自身研究的基础上降低轨道高度使卫星处于双高度段目标之间并进行了星座设计。但该研究仅针对平面覆盖情况展开设计,同时未考虑传感器有效距离,没有对于覆盖类型进行全面的讨论。
近年来,有限传感器范围的ATH问题得到了更多关注。文献[16]通过计算UTAS,LTAS,传感器范围和TL的14个交点,共给出了18种不同的双高度段平面覆盖情况及对应的覆盖面积函数。同时,利用该方法对给定目标双高度段和传感器范围情况下使得覆盖面积最大化的最优卫星轨道高度进行了计算。然而,该研究只能用于平面内的ATH问题,由于二维平面覆盖最优性并不能直接映射到三维空间的最优覆盖性,故文献[16]所给出的平面覆盖面积的求解方法不能用于三维空间覆盖体积的计算。而随后采用切片思想建立的由不同平面叠加而成的三维体积计算方法在计算效率和误差方面均存在不足[17],因此也没有针对空间覆盖的最优卫星高度进行研究。现有文献尚无专门针对双高度段ATH的三维覆盖体积的精确计算这一复杂问题的专门研究。
针对上述问题,本文提出了一种基于分段积分函数的ATH双高度段平面覆盖面积和空间覆盖体积的求解方法。该方法的基本思路如下:首先,根据遥感卫星观测轨道高度与目标球面高度的相对位置关系和传感器范围是否涉及地球遮挡区域,将单高度面覆盖问题分为四种情况进行分析,得到单高度面覆盖地心角计算公式;然后,将覆盖地心角作为被积函数,扩展到双高度段极坐标和球坐标下平面和空间的分段解析积分函数;最后,结合实际双高度段ATH问题不同组合情况,并给出其具体计算公式。通过将由积分得到的平面覆盖面积与文献[17]中的解析方法进行比较,证明了本文方法的有效性。
2 双高度段ATH覆盖的积分函数
设卫星观测轨道半径为RSat,目标高度上限为RUtas,目标高度下限为RLtas,地球同心球面半径为RThs,传感器范围为RSen。实际应用中,上面各项参数为已知参数。为了求解[RLtas,RUtas区间的平面区域和空间体积覆盖,首先需分析卫星对单个TAS的覆盖情况。
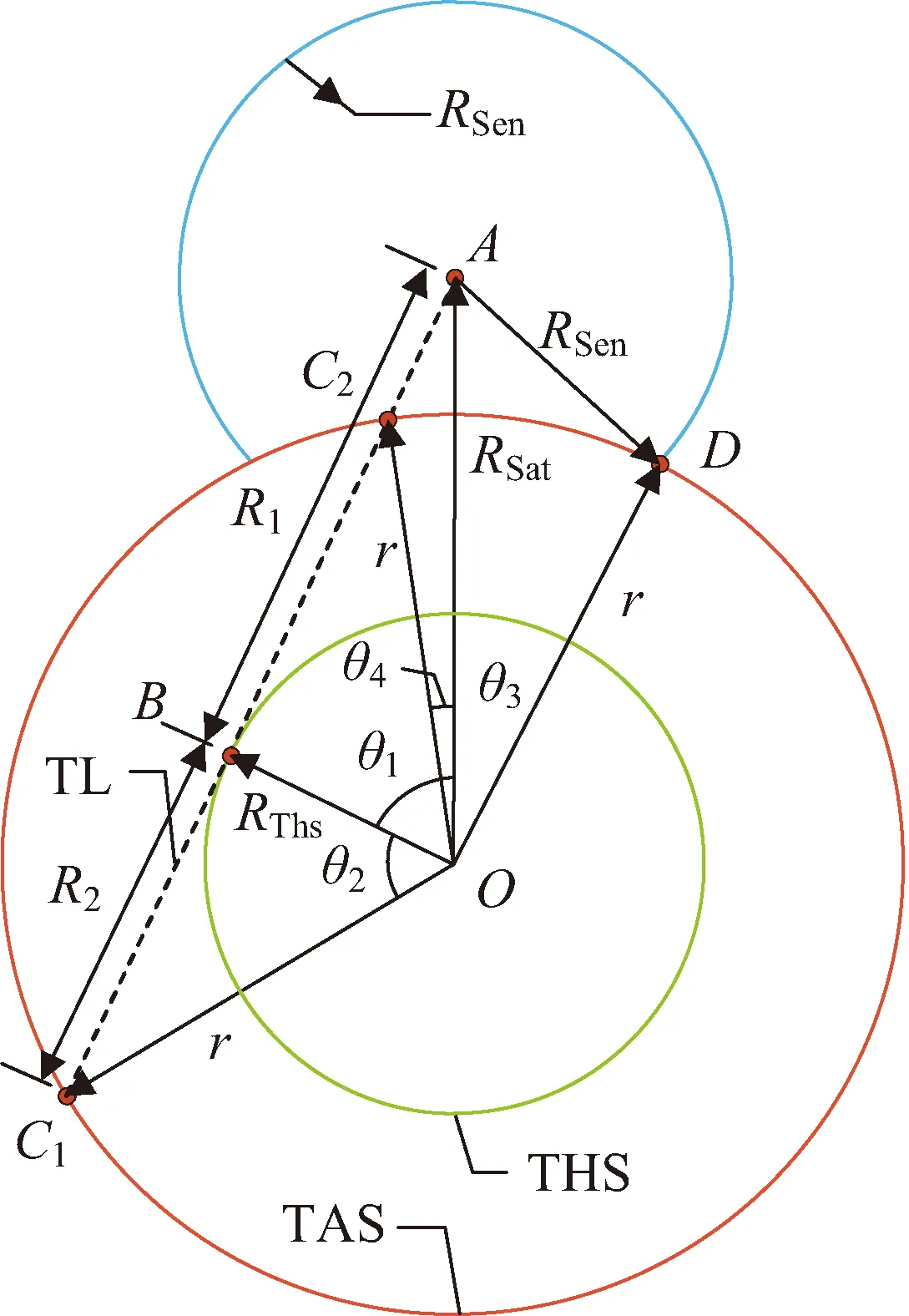
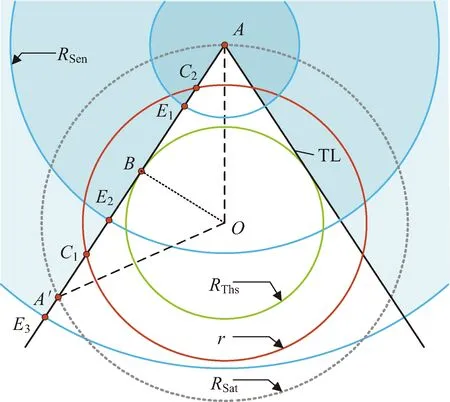
设TAS的半径为r,根据RSat和r的相对高度位置关系,存在的两种情况:①RSat≤r,卫星轨道不高于TAS,单高度球面覆盖区域不考虑THS影响;②r 针对RSat≤r的单高度球面ATH覆盖问题(见图2),定义4个位置点:卫星所在位置A,TL与THS切点B,由A点出发的切线TL与TAS交点C以及传感器最大范围与TAS交点D。 图2 单高度球面ATH平面覆盖(RSat≤r)Fig.2 ATH coverage of TAS(RSat≤r) 通过4个位置点定义辅助变量:卫星位置A与切点B的距离R1和对应地心角θ1;TL与TAS交点C与切点B的距离R2和对应地心角θ2;卫星位置A与传感器和TAS交点D对应地心角θ3。这里的交点和切点均关于地心与卫星连线OA对称,本文只取其中一点结合覆盖的对称性进行计算。 由于RThs、RSat和r三者相对位置关系固定,分析由RSen取值不同造成的影响。已知TL与THS相切,通过图2中几何关系可以得到 由三角形余弦定理,地心夹角θ3为 由于地球遮挡的影响,RSen>R1+R2后传感器范围的增长对于覆盖区域没有影响,也即传感器范围达到了THS视线遮挡的有效增长上限。因此,ATH覆盖区域对应地心角θ分情况1和2来讨论,表示为 (1) 式中:情况1中单高度面的覆盖地心角θ的端点C由传感器范围决定;情况2中单高度面的覆盖地心角θ的端点C由切线TL决定。 通过式(1)可以得到计算目标面半径r≥RSat时给定区间[RL,RU中任意单高度面的覆盖地心角θ。为了得到该区间的平面覆盖面积,在极坐标系下将其扩展到二维平面(如图3所示,由内到外依次为A(2)和A(1)情况)。极径r即为目标球面半径,极角α根据对应覆盖地心角θ选取,此时的平面覆盖面积表示为 (2) 图3 [RL,RU]区间ATH平面覆盖(RSat≤r)Fig.3 Planar ATH coverage of the dual-altitude band defined by [RL,RU](RSat≤r) 结合式(1)(2)可以得到情况1和情况2的平面覆盖面积A(n),表示为 式中:RL1、RU1为情况1的目标高度上下限;RL2、RU2为情况2的目标高度上下限。 针对给定区间[RL,RU,在球坐标系下将平面覆盖扩展到三维空间覆盖,如图4所示(情况1)。 图4 [RL,RU]区间ATH空间覆盖(RSat≤r)Fig.4 Spatial ATH coverage of the dual-altitude band defined by [RL,RU](RThs 计算点到原点的距离r即为目标球面半径,天顶角α取为对应覆盖地心角θ的一半。考虑到全向天线假设,单高度面覆盖区域扩展到三维空间后由球冠构成,即方向角β取为[0,2π]。此时的空间体积覆盖表示为 (3) 结合式(1)(3)可以得到情况1和情况2的空间覆盖体积V(n) r θ4=θ1-θ2 图5 单高度面ATH平面覆盖(r 同样,考虑由RSen取值不同造成的影响,分为情况3和4来讨论,得到覆盖地心角为 (4) 式中:情况3中单高度面的覆盖地心角θ的端点C2和D分别由切线TL和传感器范围决定;情况4中单高度面的覆盖地心角θ的端点C1和C2均由切线TL决定。 在极坐标系中考虑r (5) 图6 [RL,RU]区间ATH平面覆盖(r 结合式(4)(5)可以得到对应情况3和4下的平面覆盖面积A(n) 式中:RL3、RU3为情况3的目标高度上下限;RL4、RU4为情况4的目标高度上下限。 只存在单个情况时, RLn=RLTAS且RUn=RUTAS 当两者同时存在时, RL4=RLTAS,RU3=RUTAS,RU4=RL3= 单高度面覆盖区域扩展到三维空间后同样需要减去BTH覆盖区域。针对r V=∭dxdydz= (6) 图7 [RL,RU]区间ATH空间覆盖(RThs 结合式(4)(6)可以得到对应情况下的空间覆盖体积V(n) 以上讨论了4类不同情况下单高度面的覆盖地心角θ,并在此基础上推导了以目标高度半径r为变量的平面和空间覆盖区域的分段解析积分函数,实际的双高度段ATH覆盖问题则由这4类情况组合构成。下面将针对不同组合情况进行讨论。 为了方便讨论,先针对RThs、RSen和RSat决定的传感器覆盖区域类型进行分析并确定其构成,再考虑目标高度段[RLtas,RUtas]与传感器覆盖区域的位置关系。 定义两个新的位置点:①传感器范围与TL交点E和②A点关于OB的对称点A′。图8展示了不同传感器范围下E点的分布情况,Ei,i∈{1,2,3}。同时根据上文讨论的4种覆盖情况的切换点以及传感器范围设定4个高度辅助变量: 1)a=max{RSat-RSen,RThs},为传感器覆盖高度下限; 2)b1=RSat,为传感器中心点即卫星轨道高度; 图8 传感器覆盖区域类型Fig.8 Coverage regions of different sensor ranges 4)c=RSat+RSen,为传感器覆盖高度上限。 根据RThs、RSen和RSat与切线TL的几何位置关系,E点存在3种情况: E点位于A点与B点之间,如图8中E1点所示。 由于C1和C2关于OB对称,A和A′关于OB对称。后续讨论中仅说明其中一点位置,另一点由对称关系得出。目标覆盖区域类型取决于C2点与E点关系。 在给定RLtas和RUtas高度限制后,此时所有可能的双高度段的覆盖区域由情况1和3两部分组成,具体判断RLtas、RUtas与b2、b1、c数值大小之后,可得到该类传感器覆盖区域情况下3种双高度段的覆盖情况,详见表1。 E点位于A′点与B点之间,如图8中E2点所示。 对考虑RLtas和RUtas高度限制的双高度段覆盖由情况1,3和4三部分组合构成,具体判断RLtas、RUtas与a、b2、b1、c数值大小之后,可得到该类传感器覆盖区域情况下6种双高度段的覆盖情况,详见表1。 E点位于AA′延长线上,如图8中E3点所示。 此时所有可能的双高度段的覆盖区域由情况1,2和4三部分组成,与情况2的区别在于b1与b2的数值关系,即[b1,b2]段的覆盖类型。具体判断RLtas、RUtas与a、b2、b1、c数值大小之后,可得到该类传感器覆盖区域情况下6种双高度段的覆盖情况详见表1。 表1 不同约束参数下双高度段覆盖情况 综上,共得到15种可能的双高度段覆盖情况以及其对应的10类平面和空间覆盖区域计算公式,几何构型如图9所示。因此对于任意目标区域的覆盖问题均可通过本节的积分方法进行求取,进而可对传感器范围和卫星轨道高度进行组合优化设计。 图9 对应编号情况的几何构型Fig.9 Geometric configuration of the corresponding cases 本算例在给定任务目标的前提下,设定不同的传感器范围和卫星轨道高度,对于表1中的15种参数取值对应的10类积分情况进行具体说明分析,任务参数如表2所示。为避免地球表面地形和大气折射等影响,将切面半径RThs设为6 418 km。 表2 仿真算例参数 同时,以平面覆盖为例验证本文计算方法的正确性。采用文献[17]中的解析图形法将覆盖区域拆分为三角形、圆弓形并根据交点坐标对各覆盖情况进行计算,得到解析图形法与本文积分给出的平面覆盖面积如表3所示。 表3 解析与积分平面覆盖面积之差 由表3可以看出本文所提方法与参考方法之间的相对误差量级为10-15,验证了方法的精度和可靠性。 在确定计算方法的正确性后,进一步对不同卫星轨道半径RSat的平面覆盖面积AD与空间覆盖体积VD进行计算。当RSen=5 000 km时,考虑RSat在可行域[6 578,7 378] km上变化,由表1可知: 1)当RSat∈[6 578,6 708] km时,覆盖类型由情况2构成; 2)当RSat∈(6 708,6 848.94] km时,覆盖类型由情况4、2构成; 3)当RSat∈(6 848.94,6 887.72] km时,覆盖类型由情况4、2、1构成; 4)当RSat∈(6 887.72,6 928) km时,覆盖类型由情况4、3、1构成; 5)当RSat∈[6 928,7 105.41] km时,覆盖类型由情况4、3构成; 6)当RSat∈[7 105.41,7 378] km时,覆盖类型由情况3构成。 计算结果如图10所示,蓝色虚线为不同轨道高度的平面覆盖面积,黄色圆圈标注为最大平面覆盖面积;红色实线为不同轨道高度的空间覆盖体积,绿色方块标注为最大平面覆盖面积。 图10 平面覆盖最优性与空间覆盖最优性Fig.10 Optimality of planar and spatial coverage 从图10可以得出,最大平面覆盖面积ADmax=2.050 8×106km2,在RSat=6 885 km处取得。而最大空间覆盖体积VDmax=1.637 0×1 010 km3,在RSat=7 026 km处取得。由此可见,相同参数下,平面与空间最优观测轨道高度并不相同。 考虑平面和空间不同最优观测轨道高度的星座连续覆盖问题。M颗卫星对应的星座覆盖体积满足 M·VD=VCov1X+VCov2X+…+VCovNX 式中:VD为单颗卫星的空间覆盖体积;VCovNX为星座的N重目标覆盖体积。则基于单颗卫星空间覆盖体积最大化设定的星座在覆盖率上达到最优,而相同卫星数目的不同星座构型设计能够具体分配任务所需的VCovNX。 现设定一个构型码为6/2/0倾角为60°的Walker星座,考虑星座卫星轨道高度取为RSat1=6 885 km和RSat2=7 026 km的情况,分别对应上一节中平面与空间最优观测轨道高度,对于式(7)进行验证。 同样,本算例研究在该Walker星座构型下对于RLtas=6 708 km,RUtas=6 928 km双高度目标段的一重覆盖率和二重覆盖率。采用卫星轨道预报给出这两种星座在30 min内覆盖率的连续变化,较为全面地对比实际任务应用中平面与空间最优覆盖差异。评估结果如图11所示。 图11 基于平面与空间最优观测轨道高度星座的空间覆盖率对比Fig.11 Coverage comparison between constellations deployed on planar and spatial optimal altitudes 图11中蓝色虚线为RSat1=6 885 km情况下的空间一重及二重覆盖率,红色实线为RSat2=7 026 km情况下覆盖率,可以看出两者覆盖率呈周期性变化,且RSat2的实时一重覆盖率始终大于RSat1。在平面最优观测轨道高度时平均一重覆盖率为59.20%,平均二重覆盖率为8.74%;在空间最优观测轨道高度时平均一重覆盖率为62.46%,平均二重覆盖率为8.92%。进一步说明平面覆盖最优性与空间覆盖最优性的差异,在实际的星座覆盖设计中应采用空间最优观测轨道高度使覆盖效率最大化。 针对遥感卫星空间背景观测的覆盖问题,本文推导了由单高度面一维覆盖地心角扩展到双高度段二维平面覆盖面积以及三维空间覆盖体积的分段解析积分函数,并讨论了实际双高度段存在的15种约束参数情况和对应的10类计算公式。与现有研究相比,本文简化了讨论分类并将问题由单高度面圆环覆盖和双高度段平面覆盖进一步推广到双高度段空间覆盖,增加了其实际应用价值。 研究发现,对相同的传感器和目标区域,满足平面覆盖最优性与空间覆盖最优性的观测卫星轨道不在同一高度。基于空间覆盖最优的轨道高度设计的星座能够在覆盖率上达到最优,从实际应用来看则是更长的观测时间和更多的观测目标。因此,本文给出的空间覆盖计算方法及其对应的最优观测卫星轨道高度对构建最优覆盖星座具有重要意义。2.1 RSat≤r时ATH覆盖的积分函数
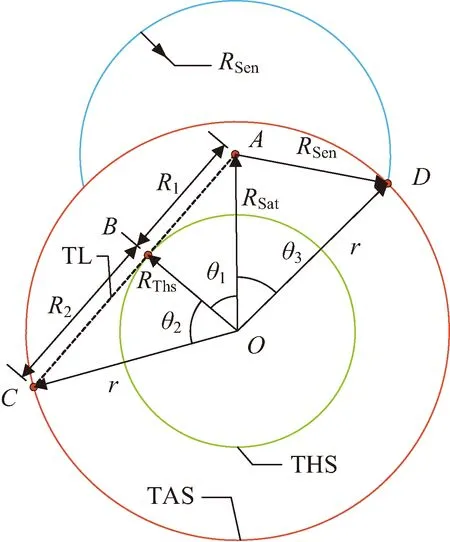
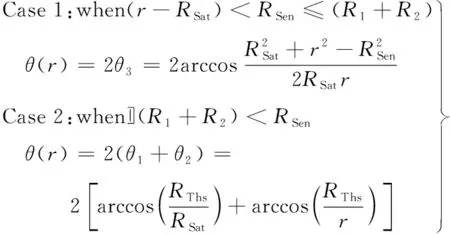
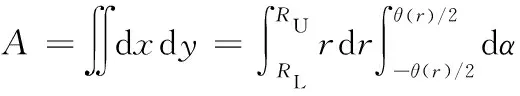

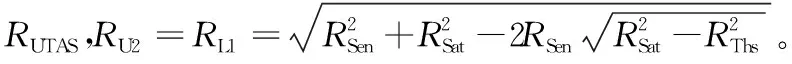
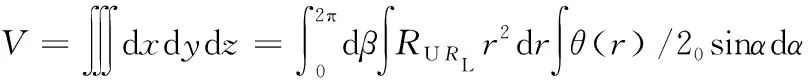
2.2 r
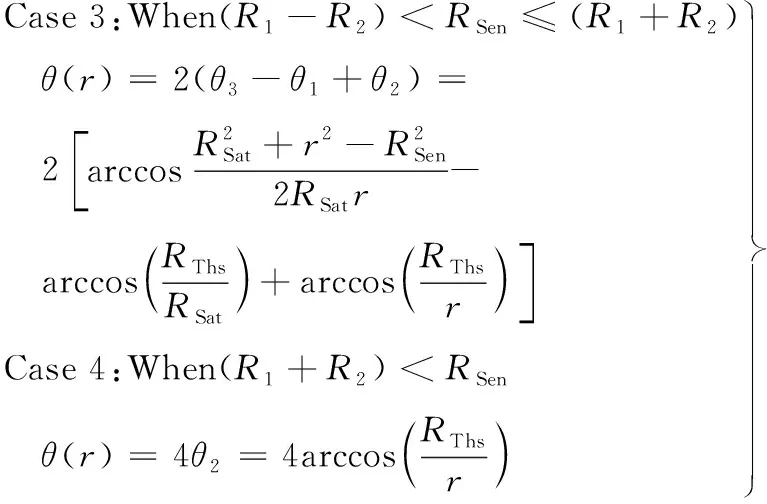

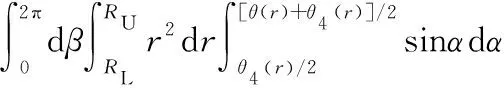
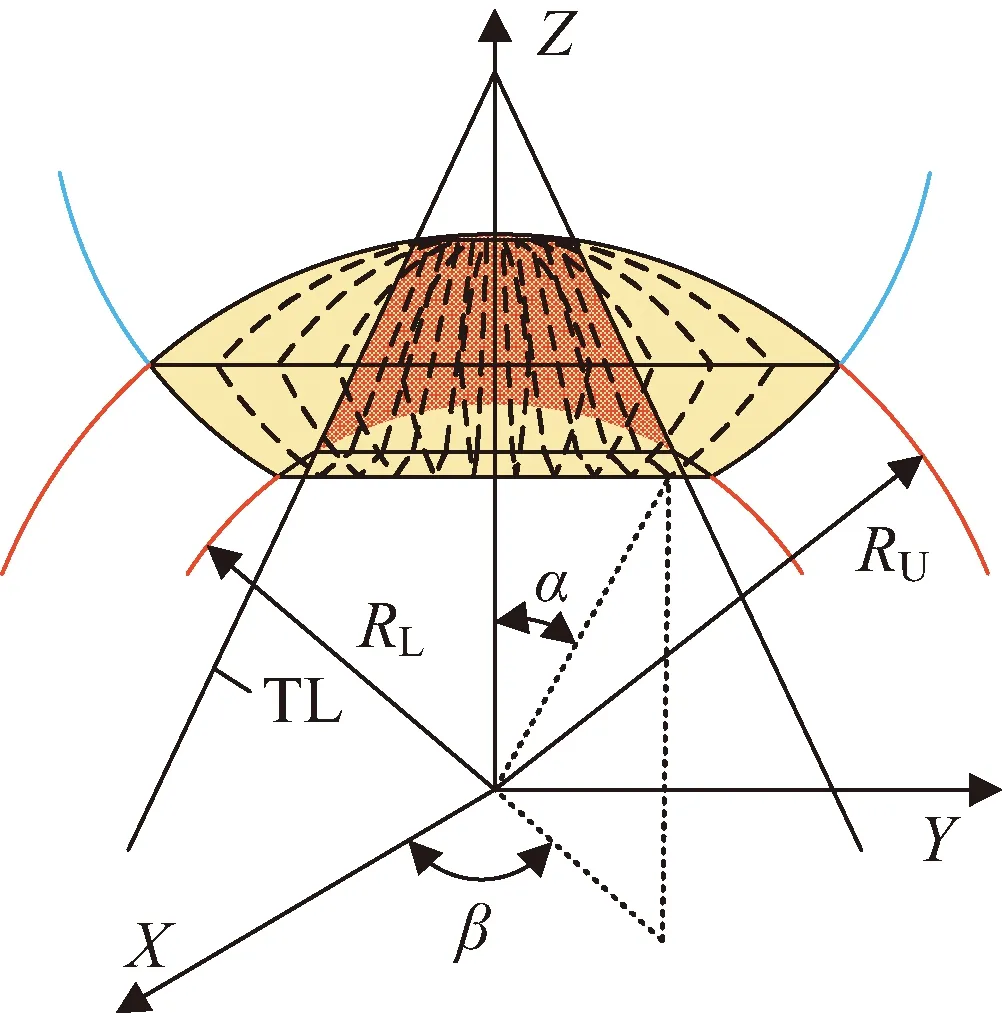
3 双高度段ATH体积覆盖计算

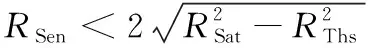
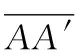
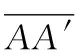
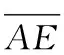
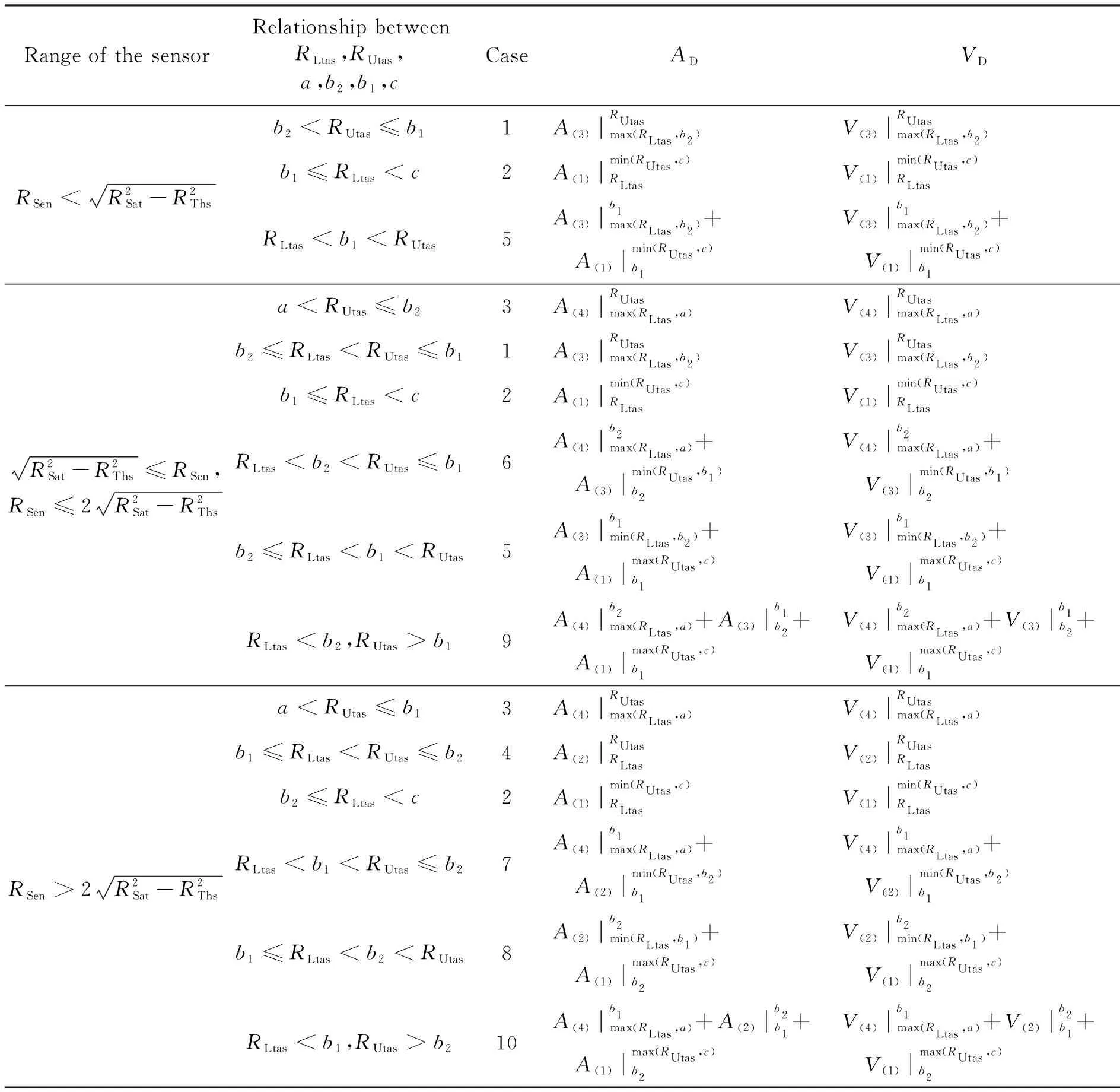
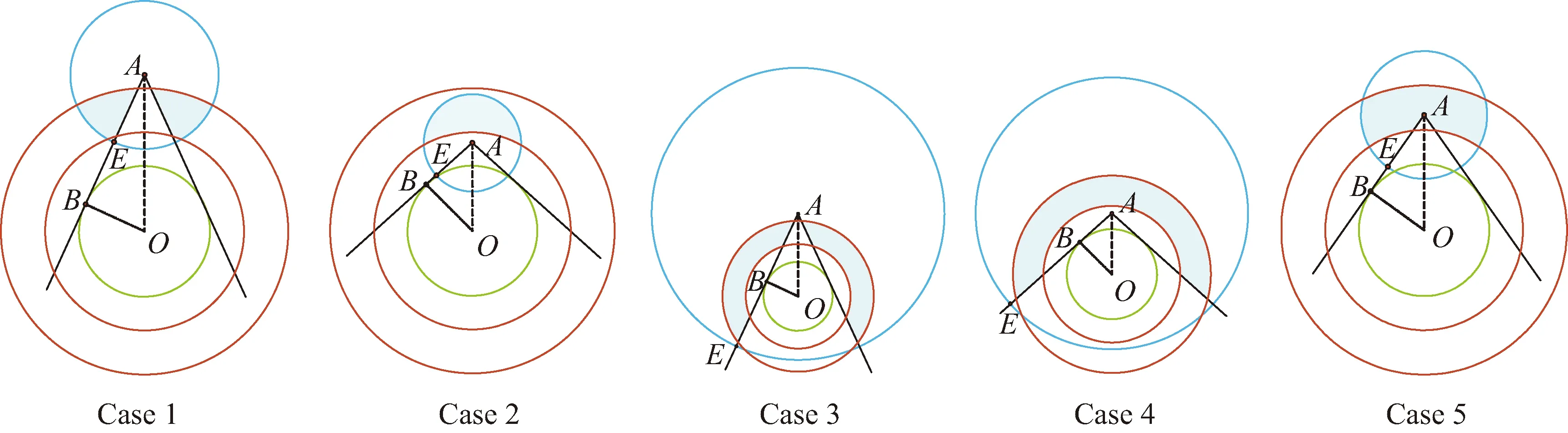
4 仿真算例
4.1 精度验证和最优观测轨道高度

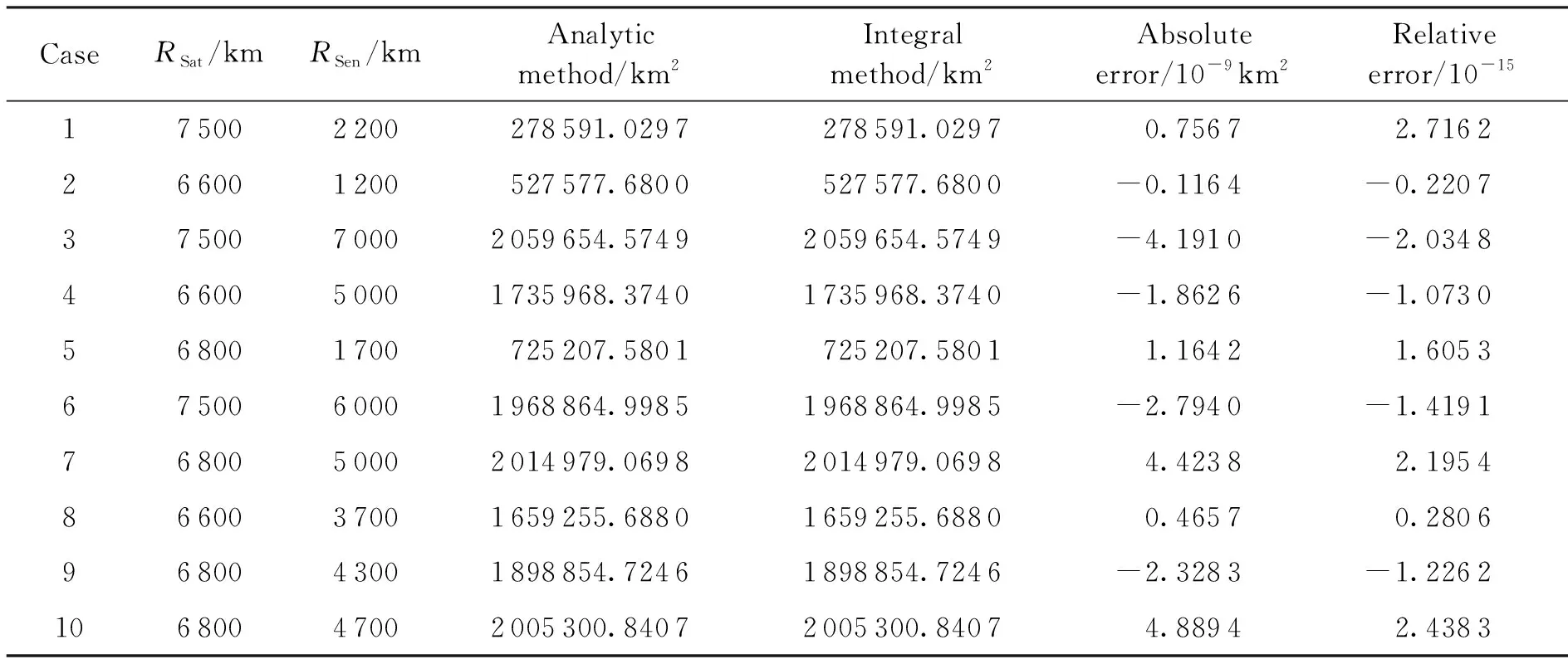

4.2 基于最优观测轨道高度的星座覆盖率

5 结论

