高空横梁弯折实验的材料力学原理分析

李 波 李晓飞

（滨州学院建筑工程学院，山东 滨州 256600）

0 引言

在人们运用材料进行建筑、工业生产的过程中，需要对材料的实际承受能力和内部变化进行研究，这就催生了材料力学。运用材料力学知识可以分析材料的强度、刚度和稳定性。材料力学还用于构件设计，使材料在相同的强度下可以减少材料用量，优化结构设计，以达到降低成本、减轻重量等目的。由此可知，材料力学在生活中的应用十分广泛。进行结构设计时，各种构件都需要满足它的强度、刚度和稳定性要求才能够安全、正常的工作，所以从力学尤其是材料力学的角度对常见构件以及生活中的结构受力现象进行分析尤为重要。在央视一热门知识类竞赛节目中，高空横梁弯折实验展示出相同截面积不同截面形式的悬臂横梁具有不同抗弯性能。本文从该实验现象背后的材料力学原理出发对其进行定量的解释和分析，以期为读者从力学角度理解该实验现象提供参考。

1 研究问题的提出与基本概念介绍

1.1 研究问题的提出

2018年9月29日中央电视台《加油向未来》第三季播放的一期节目中，其中一个题目以演示实验的形式出题：在高为4m 处有三根材料相同但截面形式不同的悬臂横梁，截面形式分别为等边三角形、工字形和正方形，依次编号为A杆、B杆和C杆，如图1（a）所示；3根横梁可伸出最大长度都是4m，且3 根横梁截面积相等均为114cm2，每根横梁自由端均坐一位实验人员并附加配重使其刚好达到120kg，横梁以适当的速度匀速伸长，让参赛者选择哪根杆可被推得最远。部分参赛者从三角形稳定性原理角度考虑选择A 杆，少数参赛者从正方形最规则这一直观认识出发选择C 杆，大部分参赛者选择了B 杆工字形截面，但是更多的是从生活经验的角度观察到工字形截面在梁中较常见。最终验证结果如图1（b）～（d）所示，当杆件伸长到120cm 处时，等边三角形的A杆断裂；当杆件继续伸长到大约160cm处时，正方形的C 杆断裂；工字形的B 杆伸长到350cm处才断裂。

图1 高空横梁弯折实验图（节目视频截图）

1.2 基本概念介绍

悬臂梁是指梁的一端为不产生轴向、垂直位移和转动的固定支座，另一端为自由端，在工程力学受力分析中，这是一种比较典型的简化模型，常见悬臂梁简化模型如图2 所示。在实际工程分析中，大部分工程受力部件都可以简化为悬臂梁[1-2]。悬臂横梁断裂的力学本质是其在端部所受最大应力超过横截面的弯曲许用应力σmax≤[σ]，最大应力计算公式如式（1）所示。

图2 悬臂梁简化图

式中：M——端部截面处弯矩，对于悬臂梁来说，即为端部集中力乘以伸出长度（力臂）；

Iz——横截面对中性轴z的惯性矩；

ymax——横截面上离中性轴最远处点的纵坐标。

惯性矩又叫截面二次轴距，惯性矩是一个物理量，通常被用作描述一个物体抵抗弯曲的能力（惯性矩示意图如图3）。惯性矩的国际单位为m4，截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩。以图3 为例，面积元素dA与其至y轴或x轴距离平方的乘积x2dA或y2dA，分别称为该面积元素对y轴或x轴的惯性矩。而以下两积分：

图3 惯性矩示意图

则分别定义整个截面对y轴或x轴的惯性矩，该积分应遍及整个截面的面积A。

2 数值计算过程与结果分析

2.1 数值计算过程

计算的等边三角形、工字形和正方形截面尺寸如图4 所示。等边三角形对于中性轴z0的惯性矩计算如下：取任意单位面积为b(y)dy。b(y)计算如式（3）所示：

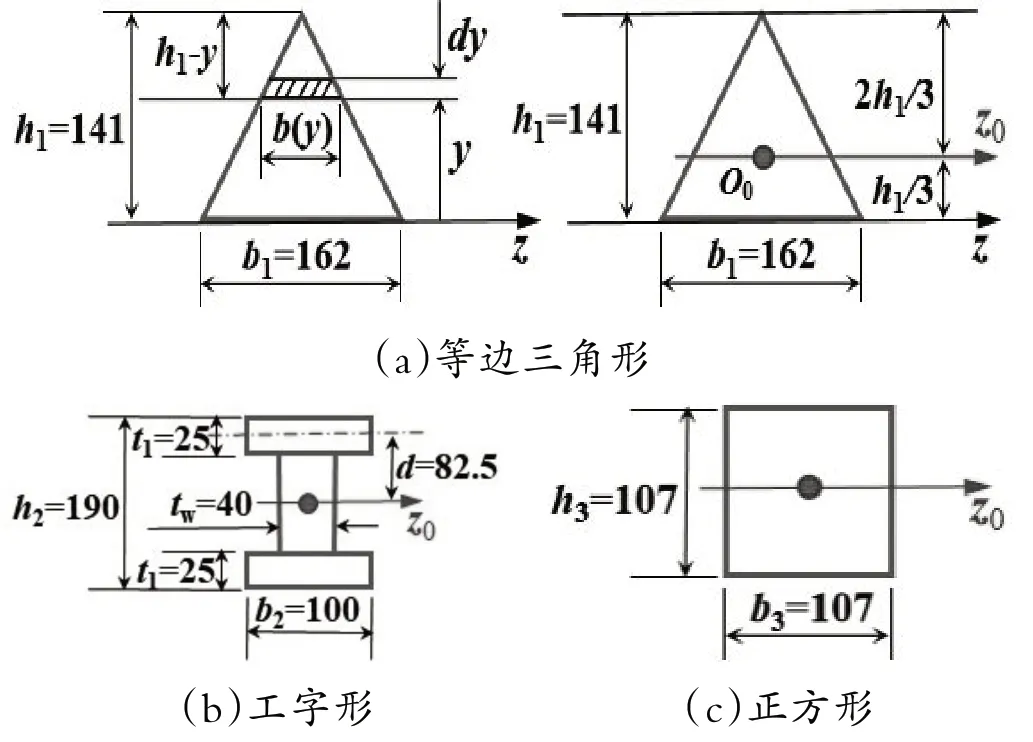
图4 不同截面形式与截面尺寸（单位：mm）

单位面积b(y)dy关于z轴的惯性矩计算如式（4）所示：

利用平行移轴公式得到该等边三角形关于中性轴z0的惯性矩计算如式（5）和式（6）所示：

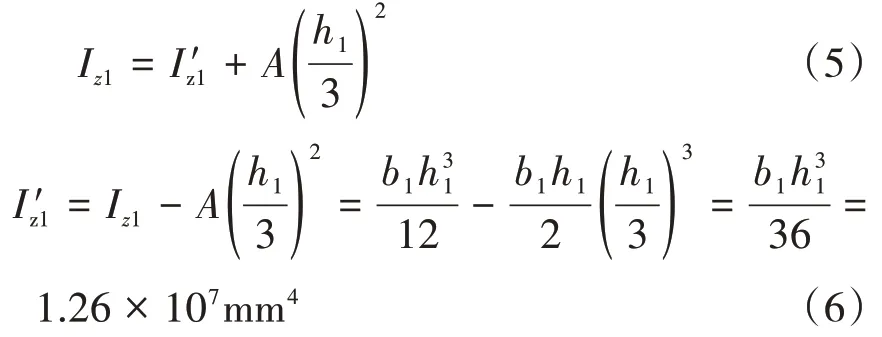
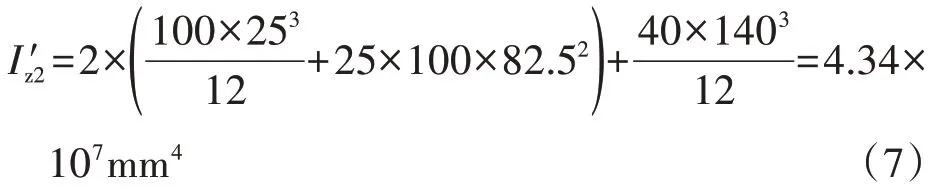
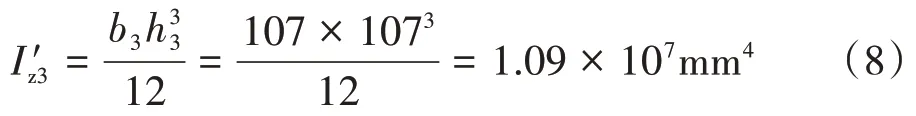
通过查阅资料可知实验所用横梁胶合材料极限抗拉强度为9MPa，且为脆性材料，可近似等于弯曲许用应力。假设断裂时，A 杆、B 杆和C 杆伸出长度分别是l1、l2和l3，端部实验人员通过配重控制恒为120kg，则可认为作用一集中力F=mg=1176N。横梁断裂时危险截面处最大拉应力达到弯曲许用应力，即σmax=[σ]，结合式（1）得到：

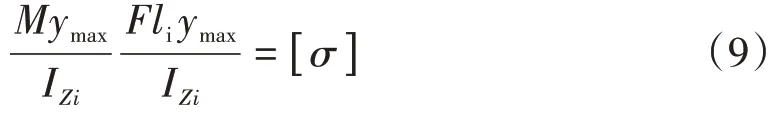
则断裂时伸出长度l1为：

带入数据得：

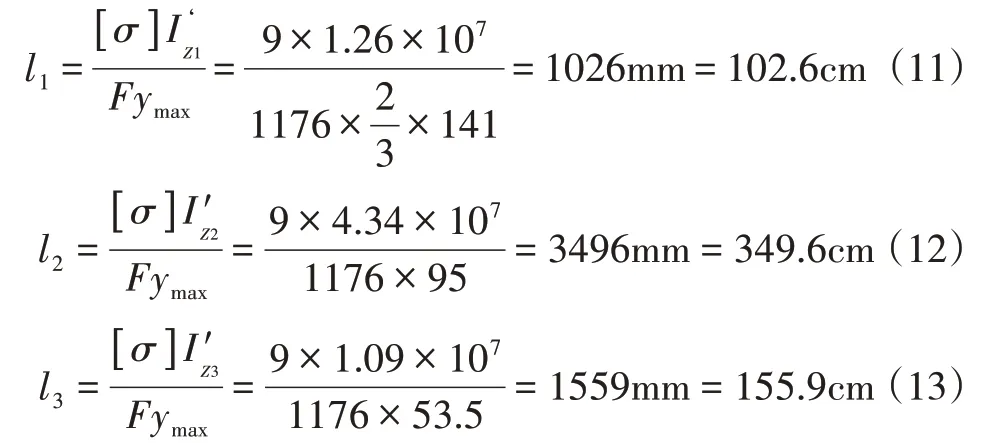
2.2 计算结果分析

由上述分析结果可知：工字形截面由于惯性矩最大，抗弯性能最好，可伸出长度l2达到349.6cm，与实际情况完全一样；等边三角形横梁最大伸出长度l1等于102.6cm，与实际断裂长度误差为14.5%；正方形截面横梁最大伸出长度l1等于155.9cm，与实际断裂长度误差为2.6%，由于杆件制作误差和人为因素等原因，计算值和实际值最大偏差不超过15%可认为在合理范围内。结果表明：惯性矩是影响构件抗弯刚度的重要因素，惯性矩越大，抗弯性能越好。同时，构件抗弯刚度还与截面形状有关，本实验对象中，等边三角形截面惯性矩虽然大于正方形，但是由于其绕中性轴为非对称结构，受拉边缘到中性轴的距离是受压边缘的2 倍，所以求得的端部受到的最大应力要大于正方形截面，所以最终伸出长度要小于正方形截面横梁。

3 结束语

材料力学通过对强度、刚度和稳定性问题的研究和分析，帮助研究人员建立起工程构件的安全性和有效性的概念，促进研究人员掌握工程构件设计的力学原理。本文以央视一热门的知识竞赛类节目为背景，基于材料力学中的弯曲理论相关知识对实验结果进行了力学原理分析与解释，并将计算值和实际结果进行了对比，结果表明理论值和实际值相符。本文为读者从力学本质出发理解不同截面尺寸抗弯性能的差异提供参考。