基于APF的AGV局部路径规划改进算法研究
丁承君,阎欣怡,2,冯玉伯,2,贾丽臻
1.河北工业大学 机械工程学院,天津 300130
2.天津通信广播集团有限公司 智慧云网事业部,天津 300143
3.中国民航大学 航空工程学院,天津 300300
AGV(automated guided vehicle)即“自动导引车”,一般来说能通过磁传感器、激光雷达等扫描周边环境生成地图,依靠地图生成路径,之后通过控制器沿规定的路径行驶,是一种高效、安全、可靠、具有柔性的移动机器人[1]。路径规划在AGV的研究领域中占有很大比重,在实际工程应用中除了在先验信息已知的建筑平面图基础上可以进行全局路径规划外,对于局部未知的障碍物又分为静态不可移动障碍物和动态可移动障碍物两种,如何在复杂的环境中规划出一条最优路径是当前AGV路径规划领域的重要问题之一。
尽管局部路径规划的环境十分复杂,但是在国内外学者大量研究的基础上也出现了一些的方法来解决这个问题。陈秋莲等[2]通过神经网络模型对障碍物进行碰撞检测,在原有粒子群算法的基础上通过调整惯性权重的方法改进,使算法可以快速规划出路径,此外将三次样条曲线平滑路径应用于静态和动态的障碍物环境。王洪斌等[3]为实现移动机器人在动态复杂环境中局部动态避障,提出将改进动态窗口算法与全局路径规划信息相结合的在线路径规划法,采用预瞄偏差角追踪法成功捕捉移动目标点,成功提高了路径规划效率。Liu等[4]提出一种改进人工势场法,当无人机遇到较大的障碍物无法前进或者当传感器受到环境因素的干扰而短暂失效时,通过扩大障碍物范围和动态改变距离,改变斥力函数使算法有效让无人机安全飞行。
人工势场法(artificial potential field,APF)是由Khatib提出的一种适用于局部路径规划的方法,可以规划出一条较为平滑的曲线避开障碍物,具有便于理解等优点,但与此同时也带来许多问题。Azmi等[5]提出了当目标被具有特定特征的障碍物阻挡时,APF方法有时会遇到无限循环问题。他们采用地图扩充的方法来重新规划,当无限循环的情况发生时,地图被转换并开始搜索可行驶路径,但是没考虑到因障碍物离目标点过近不可达问题。Wang等[6]提出了一种改进的人工势场法局部路径规划,为了使USV(unmanned surface vehicle)能够到达静态目标并跟踪动态目标,在重力场中引入了USV与目标之间的相对速度和相对加速度,但是没有考虑到算法的局限性。Ma等[7]在斥力场模型中,引入了相对位置和相对速度等影响因素,降低了目标附近障碍物的斥力势场强度,解决了目标附近障碍物不可接近的问题。引入随机扰动势能的调节机制,解决了在局部极小点难以移动的问题。然而对局部路径规划中动态障碍物的避障问题并没有给出解决方案。
在此基础上本文提出了APF改进算法,使用人工势场法并在位置势场的基础上加上了速度势场,可使AGV动态避开不同速度的移动障碍物。针对APF算法的局限性,采用粒子群算法与之结合优化算法,解决避障效果不良的问题。之所以选用粒子群算法来优化APF算法是因为AGV在局部路径规划时,所要求的时间较短,所以要选择一种收敛速度较快的算法解决在AGV避障过程中遇到的问题,而与人工势场法结合的粒子群算法和同类仿生学算法相比(见表1)具有搜索效率高、稳定性高、路径规划速度快的优势,与其他收敛速度较快的算法相比,易于改进和提高收敛效率。提高收敛效率方面,引入可调整惯性权重因子、学习因子,可以快速规划出最短路径。

表1 优化算法优缺点对比Table 1 Comparison of advantages and disadvantages of optimization algorithms
1 算法起始条件
AGV与障碍物之间的距离计算。在路径规划过程中,障碍物的形状为各不相同的不规则多边形,为了便于分析,用外接圆代替障碍物的形状,并且从安全角度[8]考虑将障碍物膨胀化处理,如图1所示。

图1 膨胀的障碍物示意图Fig.1 Schematic diagram of expanding obstacle
将膨胀后的障碍物半径设为r,障碍物的影响边距为d0,则障碍物的影响半径为ρ0=r+d0。同时AGV也用外接圆表示,其半径为ra。当d<ra+ρ0时,AGV开始进行局部路径规划。
2 人工势场法
人工势场(APF)引入了物理学中势的概念,分为引力场和斥力场[9]。与目标点之间存在引力,与障碍物之间存在斥力,两种力共同作用在AGV上,使其能安全避开障碍物。
引力场:

式中,ε是引力尺度因子;ρ(q,qgoal)表示物体当前位置与目标点的距离。
在力学中,引力场产生的引力为引力场对距离的导数:

同样的,斥力场公式:

式中,η是斥力尺度因子;ρ(q,qobs)代表物体和障碍物之间的距离;ρ0代表每个障碍物的影响半径。物体与障碍物之间的距离大小决定了斥力大小。
同理,斥力公式如下:

引力和斥力相加可得作用在AGV上的合力:

合力的方向为AGV移动的方向。
3 改进人工势场法
3.1 引入速度势场
因为障碍物在移动过程中有不同的速度,不能只用障碍物与AGV之间的距离来判断引力场和斥力场的大小,所以在原有力场的基础上引入速度势场。其斥力势场变为:

斥力变为:

式中,η1为速度斥力的尺度因子;θ为AGV指向障碍物方向与AGV运动方向的夹角,当夹角为钝角时障碍物并不影响AGV通行。用选择的目标点计算引力场及引力,其计算公式不变,在此基础上求得作用在AGV上的合力。
3.2 结合改进粒子群算法
当动态障碍物静止在路径中央,即AGV、障碍物、目标点共线时,有可能陷入局部最小值使AGV原地静止或者来回移动的情况。在障碍物运动的情况下斥力一直发生改变,不存在引力与斥力一直相等的情况,而在静态的情况下,可能会遇到引力和斥力几乎相等并一直保持,即两者达到平衡状态,不能规划出路径。当障碍物离终点过近时,也可能因为设置斥力过大,引力过小,绕过终点向无限远处移动的情况。这里计算合力和引力的夹角,当夹角快要接近180°时,即证明AGV不能到达终点。在这两种情况下使用改进粒子群算法,以小车当前位置为路径的起点,目标点为终点进行局部路径规划。
因为障碍物用圆形代替,在上述改进的基础上用插值法将一系列的位置点通过多项式拟合的方法使路径变为曲线。考虑到运算速度的问题,应选用插值公式较为简单,同时又能保证曲线光滑性的插值函数。因此相比于生成曲线更为光滑但是运算速度较慢的五次样条插值,选择三次样条曲线插值更为合适,并且三次样条曲线插值[10]引用广泛,更容易理解。
3.2.1 粒子群算法
由Kennedy和Eberhart提出的粒子群算法受到觅食的鸟的启发,每只正在觅食的鸟代表粒子群的一个粒子,这个粒子可看作在问题模型中的每一个可行解[11]。这些粒子可随迭代次数的递增不断调整自己的速度和位置[12]。在二维图中,每个粒子i在k次迭代的速度和位置分别按照下列公式进行更新:

式中,vki是粒子i在第k次迭代的速度;w是惯性权重因子,较大的惯性权重有较强的全局搜索能力,较小的惯性权重则在局部搜索方面有优势;c1、c2是学习因子,两者分别表示向自己学习能力和向群体学习能力的大小;pk-1i、pk-1g是粒子i经k-1次迭代后的个体最优解和所有粒子i经k-1次迭代后的历史最优解;rand()为[0,1]范围内的随机数;xki为粒子i在第k次迭代的位置。由式(9)可以看出,当前粒子通过上一次计算的速度、当前位置与粒子的历史最优位置、群体所有粒子的历史最优位置的距离计算更新速度,并以此速度代入式(10)不断更新位置。当达到约束条件时迭代停止。这里引入适应度函数公式如下所示:

式中,n代表粒子总数;pi代表第i个历史最优粒子的位置。
因此,适应度函数值是相邻两个历史最优粒子之间的距离和,代表了路径总长度,当适应度函数值收敛到最小且不再变化时,即路径最短则停止迭代。
3.2.2 调整惯性权重
在AGV局部路径规划时需要的时间越短越好,而当用粒子群算法规划路线时需要多次迭代收敛到最小值,因此本文在原有算法基础上引入了可调整的惯性权重因子提高算法收敛能力和运算效率。
通过文献研究发现,可通过减小惯性权重的方法提高算法的全局收敛能力,并且PSO的惯性权值为凹函数策略,优于线性函数策略,线性策略优于凸函数策略,而在凹函数中递减的指数曲线函数性能最优[13]。由此可以采取调整惯性权重的方法提高算法的收敛能力,进而提高算法的运行效率。

式中,i为当前迭代次数;K为最大迭代次数;wmax、wmin为最大、最小惯性权重,惯性权重随迭代次数的递增而不断减小。此公式原型为y=ax(0<a<1)在大于0的区间内呈指数曲线趋势递减。
3.2.3 调整学习因子
同理调整学习因子。标准粒子群算法中学习因子c1、c2取值相同,粒子在整个过程中自我认知能力和群体学习能力相同。文献[14]在此基础上证明在算法前期,粒子需要较强的自我认知能力,增加种群的多样性;到了算法后期,粒子需要较强的群体学习能力,快速收敛到最优解。
反映到c1、c2上如式(13)和(14)所示,算法前期c1>c2,算法后期c1<c2,c1呈线性递增趋势,而c2呈线性递减趋势。

然而适应度函数值的收敛曲线并不是呈线性递减而是呈指数函数趋势递减的,导致学习因子数值相等的点并不应该出现在迭代次数的中点。因此本文提出以前后两次迭代全局最优值之差的大小作为判断依据,设置学习因子的相对大小值。其伪代码如下:
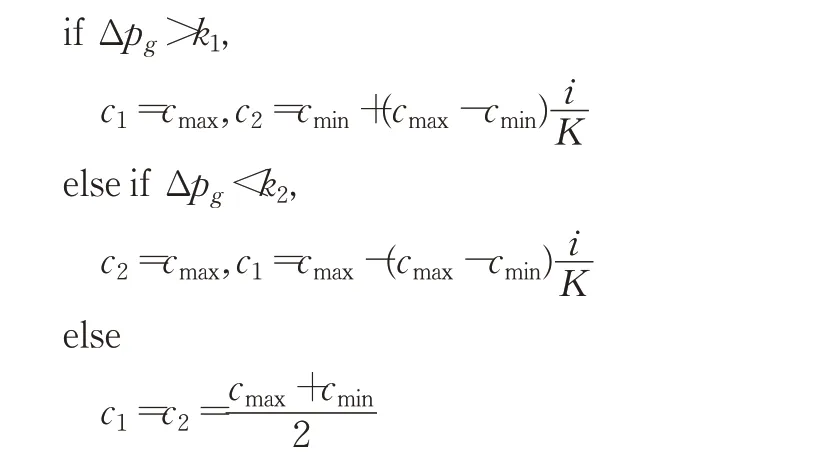
其中,Δpg为前后两次迭代全局最优值之差;k1、k2为差值常数;[cmin,cmax]为学习因子,变化范围一般为0~4。
3.3 三次样条曲线插值
设置每段三次样条曲线插值函数为S(x)=ax3+bx2+cx+d∈C(x0,xn),生成路径点为(x0,y0),(x1,y1),…,(xn,yn)。一共n+1个点,分为n个区间,每个区间上都有一个三次样条插值函数。
通过样条插值的条件来求解插值函数系数。
(1)在每个路径点处三次样条插值函数的估计值等于给定函数值。

(2)三次样条插值函数在路径点的一阶微分、二阶微分连续。

(3)使用非扭结边界条件[15],即在两个端点处的三阶导与这两端点的邻近点的三阶导相等。
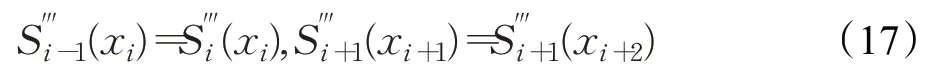
根据所列条件代入矩阵方程,计算每个样条插值函数的系数,得到三次样条曲线。
3.4 改进算法流程
算法流程如图2所示,具体步骤如下:
步骤1判断是否进入障碍物影响半径范围,进入障碍物影响范围开始局部路径规划。
步骤2改进人工势场法初始化参数,设置小车当前位置为起点,目标点为终点。设置最大迭代次数、斥力尺度因子、引力尺度因子、速度斥力的尺度因子等。改进粒子群参数初始化,设置最大迭代次数、最大最小惯性权重因子、学习因子、两次最优差值系数、种群大小等。
步骤3 AGV进入动态障碍物影响半径范围内,通过式(2)计算引力,式(6)计算斥力,式(8)计算合力。
步骤4在当前位置的基础上,加上小车速度乘以合力在x轴方向上的夹角乘以时间间隔为预测到下一时刻的位置,计算出的速度位置在下一次迭代时按公式计算引力、斥力和合力,循环往复直到达到最大迭代次数停止。
步骤4当F(q)=0(合力为0)或者cosβ<η(合力与小车和终点连线的夹角小于一定角度)时,陷入局部最小值,跳出循环。设置小车当前位置为起点,目标点为终点,运行改进粒子群算法。
步骤5按照式(12)计算惯性权重,以前后两次最优值之差作为判断依据,当差值大于设定值k1时c1=cmax,c2按式(14)计算。当差值小于设定值k2时c2=cmax,c1按式(13)计算。当差值在两个设定值之间,c1=c2。
步骤6将步骤5求得参数代入式(9),通过式(9)用上一次的粒子速度计算这一次迭代的粒子速度,再通过式(10)计算这一次迭代的粒子位置。按式(11)计算当前适应度的值,即路径长度。
步骤7当适应度的值较小时更新为个体最优,再与全局最优相比较,优于全局最优,则更新为全局最优。最后三次样条插值使路径更平滑。
步骤8输出局部路径。

图2算法流程图Fig.2 Algorithm flow chart
4 仿真验证及分析
4.1 动态环境下验证
在动态环境下仿真验证,如图3(a)所示,设置两个圆形障碍物分别沿x轴、y轴匀速运动,设置AGV起点(0,0)位于地图左上角,终点(10,10)位于地图右下角,步长为0.2 m,AGV的位置用红色小点表示。动态避障过程如图3(a)、(b)、(c)、(d)所示,分别是迭代次数为40、50、60、70的时候AGV走过的路径。由此可以看出AGV在靠近障碍物时可及时改变路径,避免碰撞的产生。

图3 动态避障过程Fig.3 Dynamic obstacle avoidance process
第一次实验设置AGV的速度v=0.5 m/s,第二次实验设置AGV的速度v=1 m/s。如图4所示,在同一中间时刻,相比于慢速下,在AGV速度更快时改进算法计算出AGV受障碍物的斥力明显增大,规划出的路径离障碍物较远。图5为不同速度下规划出的完整路径。原有的APF算法不受障碍物速度的影响,只会因障碍物的位置不同规划出不同路径。改进后的APF-PSO算法,可根据不同速度的障碍物调整AGV到障碍物的距离大小,验证了引入速度势场改进算法使AGV动态避障的有效性。

图4 迭代50次时不同速度路径对比Fig.4 Comparison of different velocity paths in 50 iterations

图5 算法终止时不同速度路径对比Fig.5 Comparison of different velocity paths at end of algorithm
4.2 静态环境下验证
4.2.1 APF-PSO算法路径规划
在静态环境下,原有的APF算法很容易受到自身局限性的影响,在达到最大迭代次数之前不能使AGV到达目标点。如图6所示,AGV当遇到局部静态障碍物距离目标点较近的时候,因斥力过大向无限远处移动而无法到达目标点的情况。图7为当障碍物的斥力与终点处的合力为0时,算法陷入局部最小值无法到达目标点的情况。在上述两种情况出现时,在原有算法的基础上引入收敛效率较高的粒子群算法可以克服原有算法的局限性,规划出局部路径。图8为面对两种情况使用APF-PSO算法规划出的路径,解决了AGV不能合理避障的问题。证明了引入改进粒子群算法的APF-PSO算法的有效性。
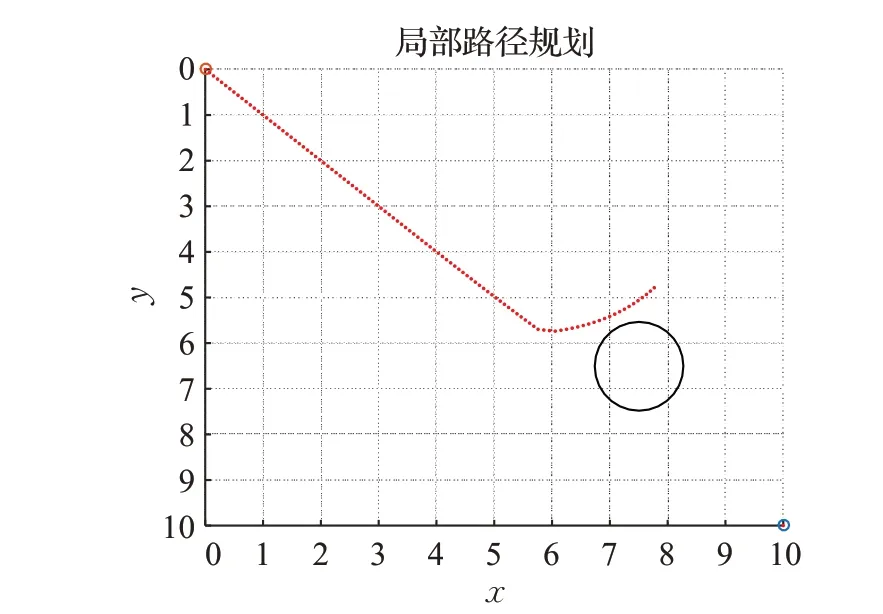
图6 传统APF算法斥力过大Fig.6 Repulsive force of traditional APF algorithm is too large
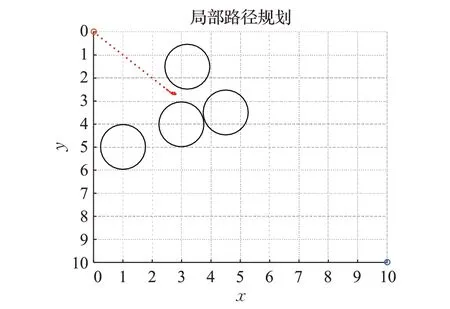
图7 传统APF算法陷入局部最小值Fig.7 Traditional APF algorithm falls into local minimum

图8 APF-PSO算法规划路径Fig.8 APF-PSO algorithm path planning
4.2.2 改进粒子群算法收敛效率验证
因为算法应用于局部路径规划,所以起点与终点的距离较短。在算法规划出路径长度差别不大的条件下主要追求算法运行效率,给予AGV充分的反应时间避开障碍物。
实验中初始化变量参数如表2所示。仿真结果如图9所示,图9(a)、(b)、(c)为蚁群算法、PSO算法、改进PSO算法在静态障碍物环境下迭代到50次时搜索到的最短路径。迭代次数相同的情况下3条路径对比,本文算法搜索出的路径最为平滑,蚁群算法和原始粒子群算法搜索出的路径还未变成平滑的曲线,未搜索到最短路径。图9(d)为3种算法收敛迭代曲线对比,图中蚁群算法在第41次迭代基本收敛,原始PSO算法第15次迭代基本收敛,本文算法在第5次迭代基本收敛,收敛速度最快,得到的路径最短。算法具体性能参数如表3所示,对比看出本文算法收敛效率最高,局部路径规划效果更佳。

图9 仿真结果Fig.9 Simulation results

表2 算法初始化参数Table 2 Algorithm initialization parameters

表3 算法性能对比Table 3 Comparison of algorithm performance
5 结束语
本文研究了一种人工势场法(APF)与粒子群算法(PSO)相融合的改进算法,针对原有APF算法应用于局部路径规划的局限性,通过引入速度势场使AGV可以动态避障。与其他算法对比,选择粒子群算法与人工势场法相融合,可以在传统人工势场法因特殊障碍物陷入局部最小值,或者障碍物距离目标点过近、斥力过大导致算法失效时,跳出算法的局限性;另外,通过调整惯性权重因子和学习因子,缩短算法运行时间,使其适用于局部路径规划。仿真结果表明,改进后的算法具有动态避障能力,解决原有算法在应用中可能导致AGV不可达的问题。

