新型承重围护保温一体化墙体抗震性能试验研究

周学军,王兴博,刘哲,2,王振,李泉,咸国栋

（1. 山东建筑大学 土木工程学院，济南 250101；2. 山东萌山钢结构工程有限公司，山东 济宁 272000）

面对日益紧张的能源问题，建筑节能受到更多重视。使用适当的保温材料可以合理、有效地利用能源，达到改善环境、节能减排、可持续发展的目的。近年来，发泡水泥作为一种耐久、耐候、耐老化性突出，防火性能优异的保温材料，越来越多地被用作建筑外保温材料[1-4]。

近年来，学者们对墙体与钢框架协同工作性能进行了相关研究。李国强等[5-6]对外挂和内嵌ALC墙板的钢框架结构进行了试验研究，认为内嵌墙板对整体刚度和承载力的贡献比外挂墙板更大，并给出了相关设计建议。曹万林等[7]、贾穗子等[8]对装配式轻型钢管混凝土框架—复合墙进行了试验研究，对比研究了结构的承载力、刚度、延性、滞回特性和耗能，分析了轻型钢管混凝土框架与复合墙共同工作的机理，提出了计算结构水平承载力的实用方法。侯和涛等[9-10]对带节能复合墙板的钢框架进行了低周反复荷载试验，强调连接件可靠度的重要性，并提出了该结构抗震设计的相关取值建议。王静峰等[11]、王波等[12]对节能复合墙板钢框架结构和填充墙钢框架结构进行了低周反复荷载试验，提出墙板连接方式和墙板厚度对结构抗震性能影响显著，认为摇摆连接件耗能性能良好，值得推广。Sun等[13]对半刚接钢框架内填带竖缝的RC墙结构进行了试验研究，分析了结构的承载力、刚度、滞回特性、延性和耗能能力，给出了钢框架和填充墙的设计建议。田稳苓等[14-15]对泡沫混凝土轻钢龙骨复合墙板进行了试验研究，提出了保温和承重双控理念，可根据墙厚和抗剪承载力要求选取不同的泡沫混凝土密度，得到了墙体抗剪承载力的实用计算方法。Xu等[16]对高强泡沫混凝土冷弯型钢复合墙体进行了试验研究，发现高强泡沫混凝土能够显著提高墙体承载力。Dall’Asta等[17]对钢框架—钢筋混凝土填充墙进行了有限元分析与试验研究，提出了一种创新的SRCW系统和相应的延性设计方法。Brodskya等[18]对砌体填充墙与钢框架之间接触的作用进行了试验研究，重点研究了填充墙和周围钢框架之间的接触区和接触压力。

然而，目前对钢框架与墙体协同工作性能的研究大多集中于钢框架与填充墙的研究，对于内部为支撑钢框架、填充发泡水泥、外部设置双向钢筋网并浇注砂浆层的承重围护保温一体化墙体鲜有研究。为实现钢结构装配式住宅墙体承重围护保温一体化的目标，提出一种带暗支撑的承重围护保温一体化墙体（以下简称一体化墙体），该墙体适用于夏热冬冷地区民用建筑。该结构将竖向承重和抗侧力承载构件与围护墙合为一体，兼具承重和保温的双重能力。这种新型一体化墙体在钢框架两侧绑扎钢筋网，浇注发泡水泥，外抹水泥砂浆保护层；为了防裂，在抹灰时粘贴耐碱玻纤网格布，起到保温、隔热、防锈、防火的作用。该结构体系既能承受竖向荷载，也可承担水平荷载。为推动该一体化墙体的应用，对6榀单层单跨一体化墙体进行低周反复加载试验，研究试件的水平承载力、抗侧刚度、滞回特性等。

1 试验

1.1 试验材料

试验设计了6榀单层单跨一体化墙体试件，墙体为钢框架浇筑发泡水泥而成，内部均设有双层双向钢筋网，外部为砂浆层作保护层，部分墙体内设置钢管暗支撑。试验参数为：有无墙体、有无钢管暗支撑、墙体高宽比。试件设计参数如表1所示。由于高宽比大于1的试件按受压设计时支撑截面过大，因此，将QB-4、QB-5、QB-6按受拉截面设计，采用交叉型支撑。试件的内部支撑形式如图1所示。

图1 试件内部构造Fig. 1 Internal structure of specimen

一体化墙体的制作流程为：1）制作热轧H型钢梁、钢管柱、钢管支撑；2）制作节点部件并将其焊接到钢框架相应位置，通过焊接方式连接梁、柱、支撑；3）制作双面双向钢筋网，并与钢框架点焊连接；4）浇筑发泡水泥墙体；5）粘贴耐碱玻纤网格布，墙面抹灰。

钢框架由热轧H型钢梁、钢管柱及钢管支撑通过节点板焊接而成，节点板为厚10 mm的钢板，并且在梁和柱连接处、梁和支撑连接处焊接加劲肋。H型钢梁的尺寸为100 mm×100 mm×6 mm×8 mm，钢柱和支撑为无缝方钢管，截面尺寸为100 mm×100 mm×4 mm，支撑截面边长为50 mm，厚度为4 mm；墙体采用密度为500 kg/m³的发泡水泥浇筑而成，两侧各铺设一层双向钢筋网，钢筋直径为2.8 mm，间距50 mm，且均粘贴耐碱玻纤网格布，外抹15 mm厚水泥砂浆。为降低试件滑移的不利影响，在试件下部设置刚性地梁。试件柱脚与刚性地梁通过12个M20高强螺栓连接，刚性地梁与地面通过地锚螺栓连接。试件几何尺寸及连接构造见图2。

图2 试件几何尺寸及构造Fig. 2 Geometric dimensions and structures of specimen

1.2 材料性能

试件所用钢材牌号均为Q235，发泡水泥密度为500 kg/m³。依据《泡沫混凝土》（JG/T 266—2011）规定，制作6块规格为100 mm×100 mm×100 mm的立方体试块，测得发泡水泥的抗压强度为2.0 MPa。依据国家标准《钢及钢产品力学性能试验取样位置及试样制备》（GB/T 2975—2018）、《金属材料室温拉伸试验方法》（GB/T 228—2002）的有关规定，每种钢材制作一组试样，进行材性试验。实测试件所用钢材的力学性能见表2。

表2 钢材力学性能Table 2 Mechanical properties of steel

1.3 加载装置及方案

试验采用低周反复加载，水平荷载采用100 t MTS作动器施加，作动器一端固定于反力墙，另一端采用高强螺栓通过加载端头与试件相连。试验加载装置与数据采集布置如图3所示。其中，水平位移和水平力均由MTS作动器采集；在墙体侧面与地梁布置位移计，以消除滑移影响；在钢支撑中部、梁中部布置应变片采集应变数据；裂缝宽度采用裂缝深度测试仪观察。

图3 加载装置Fig. 3 Test setup

试验加载过程依据《建筑抗震试验规程》（JGJ/T 101—2015），并充分考虑试验室现有仪器的相关性能，采用变幅值位移控制加载的方式，加载速率为0.5 mm/s。在试件达到屈服位移Δy前，分别按照0.25Δy、0.5Δy、0.75Δy进行加载，每级循环两周；加载至屈服位移Δy后，分别按照Δy、1.5Δy、2Δy、3Δy、4Δy、5Δy……进行加载，其中，Δy、1.5Δy、2Δy每级循环3周，3Δy、4Δy、5Δy……每级循环两周，如图4所示。在每级循环加载中，首先对试件推向加载，然后卸载，再对试件拉向加载，最后卸载。每次达到推、拉方向控制位移值后，持荷3 min。当试件发生较大变形失去承载力时，停止试验。

图4 加载制度Fig. 4 Loading system

试验前，按《建筑抗震设计规范》（GB5011—2010）中高层钢结构小震下层间位移角1/250的规定，使用SAP2000软件对各试件内钢框架进行静力弹塑性分析，结果见图5。将各钢框架荷载—位移角曲线的第一个拐点作为屈服位移的参考点，计算结果如下：QB-1～QB-3为3.0 mm；QB-4为3.7 mm；QB-5为7.0 mm；QB-6为7.0 mm。考虑到需确保在各墙体位移角1/400时有一个加载级，以便观察试验现象，最终确定各试件的Δy分别为：QB-1～QB-4为4.0 mm；QB-5和QB-6为7.0 mm。

图5 钢框架分析结果Fig. 5 Analysis results of steel frame

2 试验现象及破坏模式

试验过程中发现，QB-1在加载至19.5 mm之前，无明显现象；加载至19.5 mm时，两个支撑出现屈曲；加载至35 mm时，支撑下端与连接板的接触部位被拉断。QB-1（纯支撑钢框架）破坏模式表现为支撑屈曲破坏，支撑被拉断，最终破坏特征如图6（a）所示。

QB-2内部无钢管暗支撑，加载至2 mm时，墙体开始出现裂缝，裂缝宽度为0.2 mm；而后裂缝逐渐变多变密；加载至16 mm时，墙体开始出现较长的水平裂缝；加载至26 mm时，墙体承载力下降至峰值承载力的58.6%，试验结束。QB-2的破坏模式表现为墙体出现多条水平通长裂缝，属于剪切破坏，最终破坏特征如图6（b）所示。

加载至3.25 mm（位移角为1/400）时，QB-3无明显现象；加载至6 mm时，墙体中部开始出现斜裂缝，裂缝宽度为0.2 mm；加载至20 mm时，墙体角部出现了宽度和深度均比较大的裂缝；加载至32 mm时，墙体内传出比较大的响声，支撑被拉断，试验结束。QB-4破坏模式与QB-3比较接近，表现为先墙体破坏，后钢框架破坏的模式。高宽比较小时，墙体以剪切破坏为主，中心首先出现斜裂缝，进而裂缝发展，数量、长度均有增加，如图6（c）所示；随着控制位移的增大，由于支座处分布应力较大，墙体角部首先出现宽度较大的裂缝并发展，如图6（d）所示；在角部裂缝出现后，墙体板面裂缝不再发展，最终墙体角部发泡水泥压溃，内部钢框架的钢管支撑被拉断。

加载至10.75 mm（位移角为1/400）时，QB-6无明显现象；加载至14 mm时，墙体角部开始出现裂缝，裂缝宽度为0.2 mm；加载至21 mm时，墙体板面边缘开始出现水平裂缝；加载至77 mm时，墙体角部发泡水泥压溃，承载力降低到峰值的50%左右，试件破坏严重，试验结束。QB-5破坏现象与试件QB-6比较接近，表现为先墙体破坏，后钢框架破坏的破坏模式。墙体高宽比较大时，以弯曲破坏为主，角部、板面下部边缘处首先出现水平裂缝，如图6（e）所示；此后，随着控制位移的增大，角部裂缝和水平裂缝不断发展，最终试件角部发泡水泥压溃，如图6（f）所示。

总体而言，在加载过程中，位移角为1/400时，除QB-2（内部无钢支撑，仅作为研究对照，工程中应用墙板均有钢支撑）已产生宽度大于0.2 mm的裂缝外，其余试件（内部有钢支撑）无裂缝产生；随着各试件角部分布应力变大，角部发泡水泥破坏比较严重；在角部开裂后，发泡水泥墙板逐步退出工作，板面裂缝发展趋势放缓，直到角部发泡水泥压溃后，发泡水泥墙板基本退出工作，板面裂缝不再发展，水平荷载主要由钢框架承担。加载终止后，QB-3、QB-4板面中部在试验过程中产生的斜裂缝闭合，仅试件角部的发泡水泥压溃，如图6（g）所示。QB-5、QB-6底部梁端出现明显裂缝，如图6（h）所示，这是由于墙板角部支座处受到较大弯矩造成的。各试件试验后最终损伤照片见图7。

图6 试件试验现象Fig. 6 Test phenomenon of specimens

图7 各试件试验后照片Fig. 7 Photos of each specimen after test

3 试验结果及其分析

3.1 滞回曲线

图8为各试件实测水平荷载—位移(F-Δ)滞回曲线。可以看出：对于纯钢框架试件QB-1，其滞回曲线与其他一体化墙体有明显不同，曲线比较饱满，加载后期出现荷载突变是由于钢管支撑拉断，引起钢框架内力重分布造成的；对于QB-2，因其内部无钢管暗支撑，耗能能力较差，承载力较低，从滞回曲线整体形状来看，有一定的捏拢产生；对于QB-3、QB-4，滞回曲线的斜率先随位移的增大而增大，之后，在到达加载制度确定的位移前，曲线出现极值点，随后斜率随位移的增大而减小；在多次加载后，试件滞回曲线变得饱满，曲线介于典型钢框架试件的“梭形”和典型混凝土剪力墙试件的“Z形”之间，且更接近“Z形”，没有明显的捏拢现象，表现出一体化墙体特有的形状；每一次加载过程中，正负方向曲线峰值点连线的割线斜率均有减小；比较同级同向加载曲线，后一次加载时，曲线的斜率有明显的减小；对于QB-5、QB-6，滞回曲线变化特征与QB-3、QB-4基本一致，区别在于QB-5、QB-6的滞回曲线介于典型钢框架试件的“梭形”和典型混凝土剪力墙试件的“Z形”之间，但更接近“梭形”，这是由于QB-5、QB-6的高宽比较大，试件产生了更大的弯曲变形，耗能增加，滞回环因此不断张开造成的。

图8 试件的滞回曲线Fig. 8 Hysteretic loops of specimens

试验加载初期，墙体开裂不明显，得到的滞回环面积极小，十分狭窄，荷载—位移曲线基本呈线性变化，且几乎没有残余变形产生，试件仍处于弹性工作状态，没有能量的耗散，发泡水泥与钢框架协同变形，挤压钢框架，对钢框架起到支撑作用，此时为弹性工作阶段。加载中期，随着加载位移的增大，墙体裂缝不断增多且发展，发泡水泥逐渐退出工作，内部钢支撑开始屈服，整体结构的塑性变形开始增加，荷载—位移曲线不再呈现弹性状态时的线性，滞回环开始张开并逐渐向x轴倾斜，并且面积不断增大，耗能增大，试件整体进入弹塑性工作阶段；此时滞回曲线较为饱满，没有明显的捏缩变形，表现出良好的耗能能力；在此阶段，卸载至零时存在残余变形，说明试件的抗侧刚度有所退化。加载后期，随着加载位移的增大，试件的水平承载力和抗侧刚度不断降低，滞回环的割线斜率进一步减小，呈狭长的梭形，但仍无明显的捏缩变形。

3.2 强度退化

为定量反映试件在相同加载位移时不同加载循环的强度退化情况，定义强度退化系数λi[19]为

式中：Fi j为第j级加载时第i次循环峰值点的荷载值；Fi-1j为第j级加载时第i-1次循环峰值点的荷载值。

图9给出了6个试件的推向、拉向强度退化曲线。从图9（a）可以看出，QB-1、QB-3各加载级强度退化不显著，整个加载过程强度退化系数均大于0.90；QB-2强度退化明显，因其内部无钢支撑，泡沫混凝土墙板开裂对强度退化影响显著，在位移角达到0.5%以后，强度退化显著。从图9（b）可以看出，QB-4～QB-6强度退化曲线的变化趋势较为一致，加载初期强度退化不明显，在位移角为1.0%时，推向加载的强度退化比较显著而拉向加载的强度退化不显著；在位移角大于1.5%时，推向、拉向的强度退化显著。

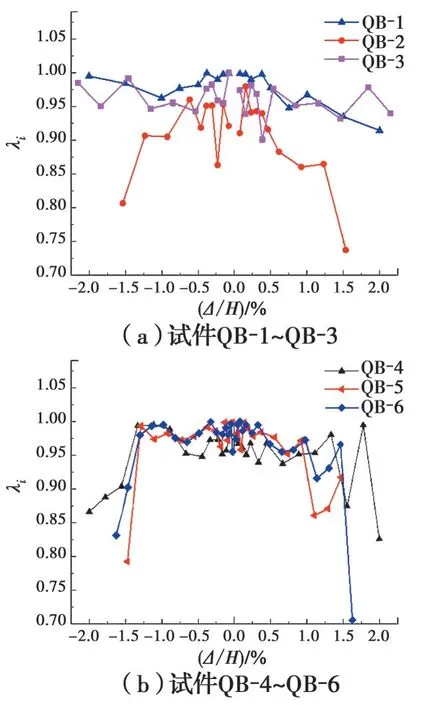
图9 强度退化曲线Fig. 9 Curves of strength degradation

3.3 骨架曲线

图10为试件的水平荷载—位移角骨架曲线。可以看出，各个试件骨架曲线变化趋势大体一致，骨架曲线在正、负加载方向具有良好的对称性。各试件骨架曲线均呈“倒S”形，说明试件受力过程可以分为3个阶段：1）弹性阶段：加载初期，发泡水泥与钢框架作为整体，共同承担水平荷载，荷载—位移曲线表现为线性比例增加。2）弹塑性阶段：弹性阶段过后，墙体板面逐渐出现斜裂缝，发泡水泥承担的水平荷载逐渐减小，曲线均出现非线性段，斜率减小，水平荷载增幅减缓，说明骨架曲线开始进入第2阶段。在这个过程中，钢框架、钢筋网与发泡水泥之间的黏结力起着维持整体共同工作的作用。随着发泡水泥承担水平荷载的减小，钢框架逐渐承担更多的水平荷载，钢管暗支撑首先进入塑性；随着墙体裂缝的增加、钢框架塑性变形增大，骨架曲线上升缓慢。3）破坏退化阶段：加载后期，试件角部的发泡水泥破坏加剧，退出工作，大部分水平荷载由钢框架承担，钢框架整体进入塑性，曲线先平缓接近平直线，后因破坏加剧导致试件水平荷载降低。

图10 试件骨架曲线比较Fig. 10 Comparison of skeleton curves of specimens

对比QB-1和QB-3的骨架曲线可以看出，QB-3极限荷载是QB-1的1.76倍，说明与纯支撑钢框架相比，一体化墙体水平承载力提高显著；对比QB-2与QB-3的骨架曲线可以看出，QB-3极限荷载是QB-2的2.18倍，说明钢管暗支撑显著提高了一体化墙体的水平承载力；QB-3极限荷载对应的位移是QB-2的1.59倍，说明钢管暗支撑对一体化墙体的塑性发展有显著的提高作用；由QB-3～QB-6的骨架曲线可以看出，QB-3极限荷载是QB-4的1.66倍、QB-5的4.03倍、QB-6的3.92倍，说明随着高宽比的增大，一体化墙体的极限荷载逐渐减小，且在高宽比大于3.8时趋于稳定。

试件屈服点计算采用通用屈服弯矩法[20]，极限位移ud取加载过程中试件破坏前一次循环的最大位移，对应的破坏荷载为Fd。各试件骨架曲线的特征点荷载及对应位移见表3。

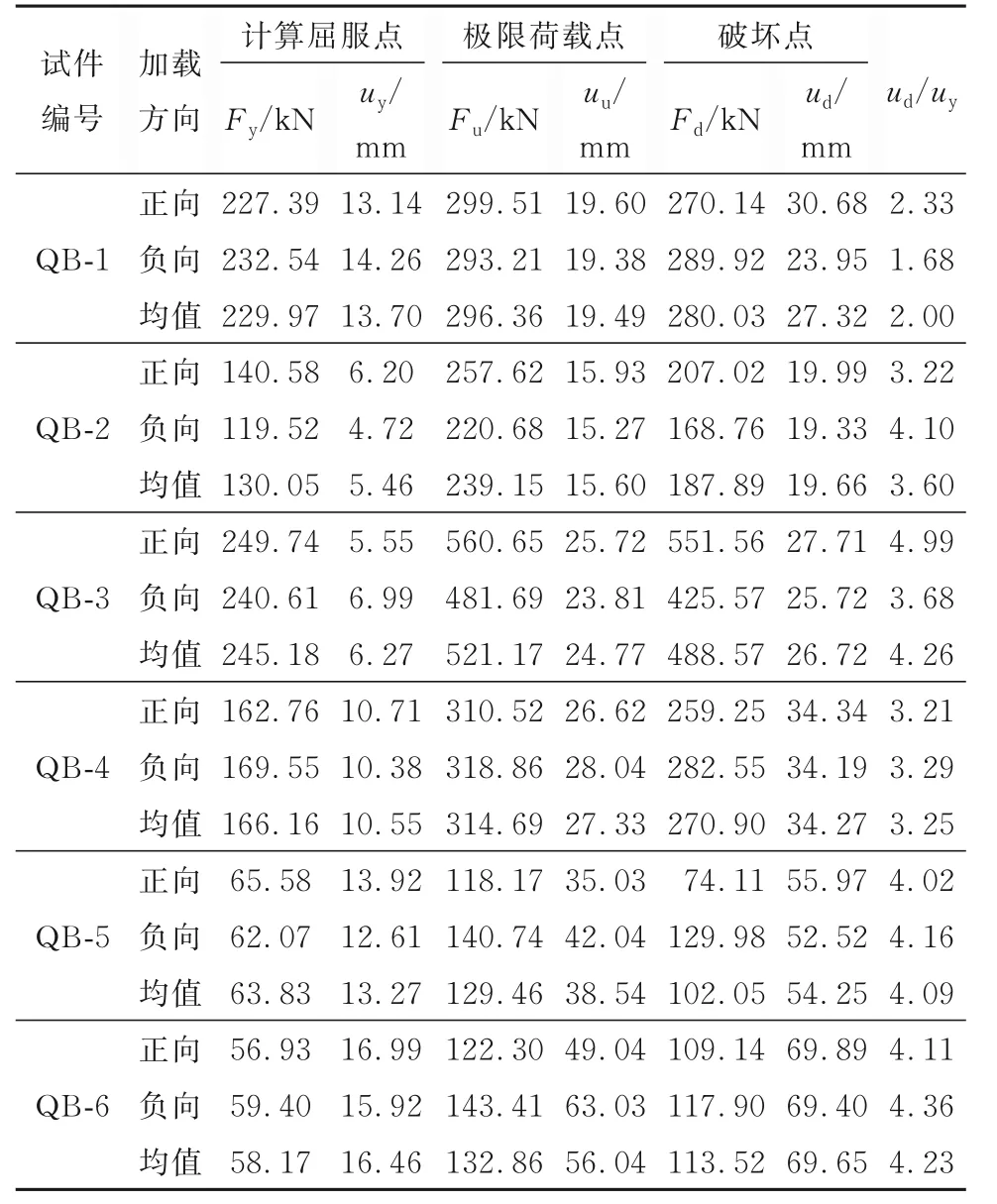
表3 试件骨架曲线特征点实测值Table 3 Measured values of characteristic points on skeleton curves

3.4 刚度退化

试件的刚度采用割线刚度Ki[19]表示，其中i为循环级数。实测各试件的初始状态、极限荷载点对应的抗侧刚度见表4。为便于分析，以试件初始刚度K1为基准点，将刚度做无量纲化处理，得到刚度比Ki/K1。实测试件的刚度比—位移角关系曲线见图11。QB-3的初始割线刚度是QB-1的2.10倍、QB-2的1.46倍，表明浇筑发泡水泥、内部设置钢管暗支撑均可以显著提高一体化墙体的抗侧刚度；QB-3的 初 始 割 线 刚 度 是QB-4的2.53倍、QB-5的10.08倍、QB-6的14.07倍，表明高宽比对一体化墙体抗侧刚度有显著影响，且墙体抗侧刚度随高宽比的增大而减小。QB-3在极限荷载点处仍有较大的割线刚度，表明QB-3到达极限荷载时仍有较好的抵抗变形的能力，安全性较好。

表4 特征点下的试件割线刚度KiTable 4 Secant stiffness Ki of specimens regarding characteristic point

图11 刚度退化曲线Fig. 11 Curves of stiffness degradation

由图11（a）可知，QB-3刚度退化速度介于纯支撑钢框架的QB-1和无钢管暗支撑的QB-2之间，并且刚度退化速度明显比QB-2慢，主要是QB-3内部钢管暗支撑显著提高了发泡水泥与钢框架的协同工作能力。由图11（b）可知：在位移角小于1/300时，曲线斜率随墙体高宽比的增大而减小，表明墙体刚度退化速率随墙体高宽比的增大而减小，主要是墙体破坏特征由剪切破坏为主逐步向弯曲破坏为主转变的缘故；在墙体高宽比为1时，实测QB-3刚度退化曲线仅出现一个下凸形状，而在墙体高宽比大于1.8时，实测QB-4～QB-6刚度退化曲线先出现下凸形状，后出现上凸形状，并且随着高宽比的增大，曲线下凸到上凸的变化越明显，表明试件刚度退化速度有“快—慢—快”三段的变化特点，并且墙体高宽比越大，“快—慢—快”三段变化特点越明显。这是因为发泡水泥受压释放孔隙体积，刚度退化出现“快”的特点；随后发泡水泥逐渐压实，刚度退化出现“慢”的特点；最后发泡水泥逐渐压溃，刚度退化再次出现“快”的特点。

3.5 变形能力及耗能

试验采用等效黏滞阻尼系数he反映试件的耗能能力[19]。实测所得各试件在极限荷载点的等效黏滞阻尼系数he和累积耗能值Et见表5，试件的等效黏滞阻尼系数he随位移角的变化规律见图12。

表5 试件在极限荷载时的耗能值Table 5 Energy dissipation values of specimens at ultimate load

QB-1极限荷载点的累积耗能值为QB-3的72%，这是因为发泡水泥与钢框架共同受力耗能，并且发泡水泥与钢材之间存在摩擦耗能，增大了结构总耗能，所以一体化墙体耗能能力显著大于纯支撑钢框架试件。QB-2极限荷载点的累积耗能值为QB-3的37%，这是因为一体化墙体内部设置的钢管暗支撑受力耗能，并且增大了发泡水泥与钢材之间的接触面积，增大了结构总耗能，所以一体化墙体内部设置钢管暗支撑能够显著提高结构耗能能力。QB-4～QB-6的等效黏滞阻尼系数he值分别为QB-3的95%、75%、74%，表明试件等效黏滞阻尼系数随试件高宽比的增大而减小。QB-4～QB-6极限荷载点的累积耗能值分别是QB-3的62%、33%、32%，表明试件极限荷载点的累积耗能值随试件高宽比的增大而减小。

由表5和图12（a）可以看出：在位移角为0.5%～1.5%时，QB-2等效黏滞阻尼系数he与QB-1基本一致，主要是QB-2内部无钢管暗支撑，在发泡水泥逐步退出工作后承载力主要由钢框架承担所致；在位移角为0～0.5%时，QB-3等效黏滞阻尼系数曲线介于QB-1、QB-2之间，有比较好的耗能能力；并且QB-3等效黏滞阻尼系数曲线在弹塑性位移角限值2%之后有比较明显的上升段，这是因为QB-3在墙板逐步退出工作后，其承载力主要由钢框架承担，表明一体化墙体在弹塑性阶段耗能性能良好，符合抗震设计“两道防线”的要求。

由表5和图12（b）可以看出：墙体高宽比为1.0和1.8时，QB-3、QB-4等效黏滞阻尼系数曲线变化趋势较为接近，表现为先随位移角的增大而增大，后随位移角的增大而减小，再随位移角的增大而增大；墙体高宽比为3.8和4.3时，QB-5、QB-6等效黏滞阻尼系数曲线变化趋势较为接近，表现为随位移角的增大而增大，表明高宽比显著影响着一体化墙体的变形形式与破坏模式。

图12 试件等效黏滞阻尼系数Fig. 12 Equivalent viscous damping coefficient of specimens

3.6 应变分析

由于各试件高宽比不同，为便于分析，以位移角为横坐标，应变比为纵坐标，对各试件内钢框架的钢支撑进行应变分析。另外，由于人字形斜撑的拉压杆应变变化具有对称性，交叉斜撑的拉压杆也具有对称性，故仅展现各试件正向加载时受拉斜撑的应变，便于比较分析。各试件钢支撑加载过程的应变如图13所示。其中，应变比为采集到的应变值与材性试验得到的钢材屈服应变的比值。

图13 钢支撑应变Fig. 13 steel bracing strain

由图13可以看出，QB-1斜撑在位移角0.5%附近（对应位移为6.5 mm）时开始进入屈服，而后应变比持续增大，最大为3倍屈服应变；QB-3斜撑在位移角1.0%（对应位移为13 mm）之后开始屈服，且正、负向加载曲线略有不同，可能是加载先后顺序所致；在整个加载过程中，QB-1和QB-3的竖撑均未屈服。交叉斜撑的测点布置在斜撑中部，QB-4内交叉斜撑在位移角1.0%（对应位移为18 mm）之后进入屈服，最大应变为1.4倍屈服应变；QB-5、QB-6内交叉斜撑在加载过程中未屈服，可能是因为试件高宽比过大、斜撑长度过长（QB-6斜撑长4 414.7 mm），破坏位置转移到底梁底部焊缝处，如图6（h）所示。

4 水平承载力计算

4.1 简化计算模型

目前，主要采用等效斜压杆模型[21-30]计算框架—墙体系的侧向承载力，等效斜压杆模型是将墙体等效成两端与框架铰接的斜压杆。根据试验，新型承重围护保温一体化墙体水平承载力的计算可采用支撑钢框架—等效斜压杆模型，计算简图见图14。如图14（a）所示，将发泡水泥和双向钢筋网外抹砂浆的墙体等效为一个斜压杆，与支撑钢框架铰接；如图14（b）所示，支撑钢框架—等效斜压杆模型的水平承载力P由支撑钢框架水平承载力Fk和斜压杆承载力R的水平分量相加所得。其中，斜压杆承载力R可按式（2）计算。

图14 水平承载力计算简图Fig. 14 Calculation diagram of horizontal bearing capacity

式中：w为等效斜压杆宽度；t为新型承重围护保温一体化墙体厚度；fc为发泡水泥立方体抗压强度。

故支撑钢框架—等效斜压杆模型的水平承载力P可按式（3）计算。

式中：θ为框架对角线与水平方向的夹角。

4.2 等效斜压杆模型水平承载力计算

等效斜压杆模型的关键是确定斜压杆的宽度。目前关于等效斜压杆宽度的计算方法主要有以下几种，曹万林等[7]提出采用斜压杆截面折算高度系数β计算等效斜压杆的宽度（高度），该系数为等效斜压杆截面高度与宽度的比值，取值与墙板构造有关，通过试验确定，并提出等效斜压杆的宽度b=βtinf，其中tinf为墙体厚度；Holmes[21]提出等效斜压杆宽度为框架对角线长度的1/3；Smith[22]、Stafford等[23]提出等效斜压杆的宽度是框架柱特征刚度参数λ的函数，可按式（4）计算。

式中：EI、E分别为墙体、框架柱的弹性模量；θ为墙体对角线与水平方向的夹角；t为墙体厚度；h′为墙体高度；I为框架柱截面惯性矩。

Kadir[25]提出采用接触长度αl、αh计算等效斜压杆宽度，如式（5）所示。

式中：αl=π/λl；αh=π/λh，其中，λl、λh分别为框架梁和框架柱的特征刚度参数，按式（4）计算。

Te-Chang等[26]提出等效斜压杆宽度与跨高比l/h有关，跨高比在1.0到1.5之间时，等效斜压杆宽度计算公式为

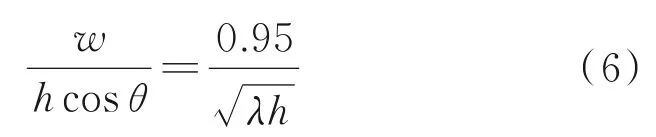
Paulay等[27]认为可以采用恒定比例近似计算等效斜压杆宽度，且认为等效斜压杆宽度为框架对角线长度的1/4；Klingner等[28]基于特征刚度参数λ，提出等效斜压杆宽度可按式（7）计算。

高润东等[29]认为等效斜压杆宽度可按式（7）计算，但在计算等效斜压杆承载力时，需乘以折减系数0.9；土耳其相关规范[30]采用的计算方法与式（7）形式相近，但调整了两个参数。

分别采用以上方法，针对一体化墙体试验试件作试算，结果见表6。

表6 不同方法计算试件承载力对比Table 6 Comparison of horizontal bearing capacity of specimens calculated by different methods

由表6可知，使用不同方法计算各试件的承载力差别很大，难以适用于不同高宽比的一体化墙体承载力计算。对已有成果进行总结分析，综合考虑一体化墙体在地震作用下的表现，结合文献[7]，提出一种基于等效斜压杆理论的实用简便的水平承载力计算方法，为一体化墙体水平承载力计算提供参考。

考虑到不同高宽比下墙板破坏形式不同，权衡结构设计的安全性和经济性，用式（9）计算一体化墙体等效斜压杆宽度。

式中：μ为斜压杆截面折算宽度系数，该系数为等效斜压杆截面宽度与厚度的比值，根据试验，考虑双向钢筋网与砂浆保护层的贡献，采用上述一体化墙体构造时，取μ=4.5；η为高宽比影响系数，依据试验，高宽比为1.0时，η=1.0；高宽比为1.8时，η=0.6；高宽比大于3.8时，η=0.4。

考虑发泡水泥、钢筋网和砂浆层对支撑钢框架的约束作用提高了一体化墙体的承载能力，为简化一体化墙体模型的承载力计算，可近似采用式（10）进行计算。

式中：Fk为支撑钢框架水平承载力；w为等效斜压杆宽度；t为新型承重围护保温一体化墙体厚度；fc为发泡水泥立方体抗压强度；θ为框架对角线与水平方向的夹角。

式（10）适用于计算内含钢支撑的承重围护保温一体化墙体，计算时材料强度取材性试验值，计算所得新型承重围护保温一体化墙体试件的水平承载力P与极限荷载试验值的对比见表7。可见，计算结果与试验实测结果吻合较好。

表7 试件水平承载力计算值与极限荷载试验值对比Table 7 Comparison between calculated results of horizontal bearing capacity and ultimate load test results of specimens

5 结论

1）在合理连接的条件下，新型承重围护保温一体化墙体的内置暗支撑和双向钢筋网外抹砂浆保护层的构造形式，能够保证其在位移角1/400前不开裂。

2）新型承重围护保温一体化墙体的水平承载力和抗侧刚度分别为纯钢框架的1.76、2.10倍，表明墙体的水平承载力、抗侧刚度相对于纯钢框架均有较大的提高，在设计中须加以考虑。

3）高宽比对墙体抗震性能影响显著，墙体的水平承载力、抗侧刚度、耗能能力均随高宽比的增大而减小。

4）对比8种计算方法，考虑高宽比的影响，提出新型承重围护保温一体化墙体水平承载力的实用计算方法，计算结果与试验结果吻合较好。