梯形蓄热罐形状对蓄热性能影响的数值研究

张 军，赵凤霞，杜 昭,，阳 康，李元基，杨肖虎

（1中国建筑西北设计研究院有限公司，陕西 西安 710061；2西安交通大学人居环境与建筑工程学院，陕西 西安 710049）

固液相变蓄热因其蓄/放热过程温度恒定，蓄能密度大和体积变化小等优点而引起众多学者关注[1-3]。相变材料熔化后受到自然对流影响[4]，相变蓄热罐内总会出现上下区域熔化速率和温度不均匀的现象[5-7]。前者会导致完全熔化时间增加，后者会引起局部热应力，降低蓄热罐的寿命。为解决蓄热罐上下区域熔化不同步的问题，近年来提出了不均匀强化的思想。对于翅片强化换热结构，多数从改变翅片分布间隔，翅片形状来优化均匀性[8-9]。Sodhi 等[10]研究了翅片分布对蓄放热过程的影响，得出结论：在单一相变材料系统中使用非均匀分布的翅片，熔化和凝固时间分别减少了24.5%和16.5%。Yang等[11]设计了不同翅片间距和位置的管壳式潜热蓄热单元的数值模型，计算结果表明，与原来的均匀翅片相比，环形翅片分布不均匀的热能存储单元使得相变材料完全熔化时间和平均温差分别减少了62.8%和34.4%。Tiari等[12]在保持翅片总体积不变的前提下比较了具有不同翅片高度的潜热蓄热系统的蓄热性能。结果表明，从底部翅片较长到顶部逐渐变短的翅片配置可使得潜热蓄热系统的蓄热时间最短，蓄热总时间减少为原来的73.7%。

此外，一些学者通过设计梯度参数的泡沫金属对蓄热均匀性进行优化[13-16]。何贤德[17]在研究中发现泡沫金属孔隙率的变化对熔化相界面的移动有很大影响；孔隙率越大，相界面倾斜角度越大，均匀性越差。为改善该现象，设计了梯度变化的孔隙率，模拟结果表明该梯度设计的孔隙率较均匀。就孔隙率而言，蓄热速率提升了142%。Marri等[18]比较了具有0.90、0.94 和0.97 三种不同孔隙率的开孔铝泡沫蓄热罐内熔化蓄热工况，结果显示：与均匀孔隙率相比，具有不均匀孔隙率的设计显示出高达28%的性能提升。

回顾以往的研究发现，虽然通过非均匀布置翅片或泡沫金属结构可有效改善蓄热罐上下区域熔化不均匀性，但向蓄热罐中添加额外的换热结构势必减小了蓄热材料的填充量，同时增加了蓄热罐质量。受到以往非均匀强化结构的启发，本工作提出通过改变蓄热罐形状来改善蓄热罐蓄热过程表现出来的不均匀性，设计了一种梯形结构的蓄热罐，通过充分利用熔化区上部自然对流的传热机制与下部导热为主的传热机制，上下形成梯度形状以实现蓄热过程上下区域的同步协调，为蓄热罐的结构设计与运行提供理论指导。

1 相变蓄热数值模型设计

1.1 数学模型与数值模型

本工作采用ANSYS-Fluent 18.2中的Solidification/Melting 模型进行瞬态传热计算。同时也做了以下假设：

（1）对相变材料的密度变化采用Boussinesq假设；

（2）假设相变材料熔化后的液相为不可压缩牛顿流体；

（3）相变材料的物性为均匀物性且各向同性。

基于上述假设，本工作的控制方程如下：

连续性方程：

本工作提出通过改变蓄热罐形状改善蓄热均匀性的构想，以竖直壳管式蓄热器为基准开展改良设计和对比分析。如图1(a)所示，竖直壳管式蓄热单元由两个同心圆柱体组成，外侧圆柱体由亚克力制成，内径为45.0 mm；内侧圆柱体由铜管制成，外径为11.0 mm，厚度为1.0 mm，整个蓄热罐高度为270.0 mm。为了缓解熔化过程中出现的不均匀性，本工作提出的新型梯形蓄热罐结构如图1(b)所示。在保证石蜡填充高度、含量与基准模型不变的情况下，计算得到梯形蓄热罐顶盖半径长度(定义为R1)、底盖半径长度(定义为R2)数值。本工作共设计5 个模型，详细设计尺寸如表1 所示。由于所设计模型为轴对称图形，且数值计算所得物理场沿着任一过对称轴的平面切开均为相同的对称图形，所以本工作选取所切平面的一半为计算域。如图1(c)所示，简化后的计算域为二维平面图形，包含一半的传热流体通道、铜管壁厚和一半的相变材料区域，该简化结果不仅可以节省计算量而且不影响观察物理规律。

图1 竖直壳管式蓄热模型示意图Fig.1 Schematic diagrams of vertical shell and tube heat storage models

表1 梯形蓄热罐详细尺寸表Table 1 Detailed size of the trapezoidal heat storage tank

表2 蓄热材料物性参数表Table 2 Physical properties of heat storage material

1.2 网格无关性与时间步长独立性验证

为了消除网格数量与时间步长对数值结果的影响，选取模型2 进行计算，对比了3 组不同网格数和时间步长的计算结果，如表3所示。从表中可以看出，以8000 s 时的熔化率为评价指标，网格数为83514在8000 s时的熔化率为0.353，进一步增加网格数到156938，此时的熔化率为0.348，两者相差1.4%，符合误差要求范围，为了节省计算资源，本工作选择网格数为83514进行计算。在确定网格数后，又设立了3组时间步长，分别为0.05 s、0.10 s 和0.50 s，经过计算可以发现时间步长为0.10 s在8000 s时的熔化率为0.353与时间步长为0.05 s 时在8000 s 的熔化率0.352 相差0.3%。为了尽可能节省计算时间，所以本工作选择时间步长为0.10 s进行计算。

表3 网格无关性与步长独立性Table 3 Mesh independence and step independance

1.3 数值模型验证

为了验证本工作数值模型的正确性，选取Longeon 等[19]针对同心套管式蓄热器[图1(a)]的蓄热实验进行对比验证。图2展示了同一测点温度实验结果与模拟预测的对比。该测点位于同心套管中部，距离顶部183.0 mm，距离铜管外壁径向距离为6.6 mm。通过对比发现模拟结果与实验结果吻合度良好，在2500 s 之前和4500 s 之后均重合，在2500～4500 s 之间出现偏差，经过计算最大偏差为5.4%，证明了本工作数值模型的可靠性。

图2 模型验证图Fig.2 Curves of model validation

2 数值模拟结果分析

2.1 完全熔化时间与熔化率

图3 展示了5 个模型的完全熔化时间，可以看出，将相变材料移到上部区域有利于减小完全熔化时间，即模型1 和模型2 的完全熔化时间均小于模型3 的完全熔化时间。其中，模型1 的完全熔化时间最短，为17240 s，较基准设计模型3 的完全熔化时间28290 s 节省了39.06%。而增加下部相变材料会导致完全熔化时间增加，因此，模型4和模型5 需要更长的时间达到完全熔化，模型5 的完全熔化时间为41350 s，较模型3增加了46.16%。该现象也说明改变蓄热罐形状对完全熔化时间产生极大的影响，这主要归因于相变材料的不均匀分布与蓄热罐内部自然对流对高温流体不均匀分布两者的重合度。若大量相变材料分布在高温流体区域，有利于及时将热量传递到固态相变材料区域，因此完全熔化时间减少。

图3 完全熔化时间Fig.3 Complete melting time of 5 models

为了更详细地观察蓄热罐内熔化规律，图4展示了不同模型熔化率随时间的变化曲线，通过熔化全过程分析不同模型熔化快慢原因。从图中可以看出，在500 s 之前，5 个模型的熔化率曲线几乎重合在一起。这主要是因为熔化刚开始阶段蓄热罐内为固态相变材料，热量主要依靠导热进行，只有靠近铜管的石蜡被加热熔化，因此不同比例的新型蓄热罐对于石蜡的熔化速率不产生影响。在500 s 以后，不同模型的熔化率曲线开始表现出差异，并且随着熔化不断进行，熔化率曲线的差异越来越大，其中模型1 的熔化率曲线斜率最高，模型3 的熔化率曲线斜率最低。在2500 s 以后，模型1、模型2和模型3 的熔化速率加快；在11800 s 时，模型3的熔化率超过了模型4和模型5，并且持续到最后。这得益于持续导热导致液态区域增大，自然对流增强，相变材料的熔化速率加快。然而，模型4和模型5的熔化速率开始逐渐减慢，这是因为自然对流导致高温液态相变材料在上部，而多数相变材料聚集在下部区域，两者之间的传热距离较大，不利于传递热量到未熔化区域。

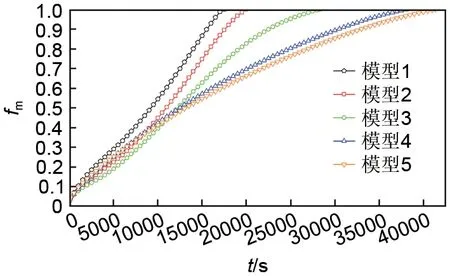
图4 不同模型的熔化率曲线Fig.4 Melting rate curves of 5 models

在500 s 到7500 s 的时间段内，5 个模型的熔化率曲线表现出很大的差异，其中模型1熔化得最快，模型3熔化得最慢，且两者差距较大。在500 s到7500 s的时间段之间，模型1、模型2、模型4、模型5 均表现出比模型3 较快的熔化速率，这主要是因为对于模型1、模型2、模型4、模型5 这4 个模型采用了新型蓄热罐，在上部或下部存在相变材料存储较少的狭窄区域，且其接触周围相变材料的面积也小。所以相同热量传递到该区域，由于与周围接触面积小热量不易扩散，导致温度上升较快，熔化速率在初期较快。这一现象在相界面云图也可以得到证明，1000 s时模型1和模型2下部区域的液态区域面积要大于模型3 下部区域的液态区域面积。

图4 中模型3、模型4 和模型5 在熔化率达到0.75之后会出现熔化速率大幅下降的现象，但模型1和模型2并未表现出熔化速率大幅下降的现象，这是因为按照模型1 和模型2 的上下半径比例在熔化结束阶段仍有利于将热量传递到难熔区域。

2.2 相界面

图5 展 示 了5 个 模 型 在2000 s、8000 s 和14000 s 三个时刻的熔化相界面。从图中可以看出，在2000 s 时，模型2、模型3 和模型4 的相界面大致相同，都是靠近铜管处的相变材料发生熔化，并且在微弱自然对流的不断冲刷下，上部相变材料出现小区域的液态区。模型1除了上部出现小区域的液态区外，下部同样出现了液态熔融区域。这主要是因为模型1的设计为下部狭窄，逐渐向上部扩宽的形状。这导致下部区域的相变材料较少，并且与上部接触面积较小，同样热量传递到相邻相变材料的量也较少，所以该处相变材料会先熔化。这一观点也可以在熔化率曲线图中得到印证，存在狭窄区域的模型1、模型2、模型4和模型5在熔化初期，熔化率曲线总是高于模型3。

图5 5个模型的相界面云图Fig.5 Melting front contours of 5 models

在8000 s时，5个模型的相界面差异变大。从图中可以看出，从左往右，模型1 到模型5 的两相交界面逐渐下降，但值得注意的是这并不代表模型4 和模型5 熔化速度快，此观点可以在熔化率曲线图中得到印证。相界面下降这一现象主要是从模型1 到模型5 的变化过程来看，相变材料在蓄热罐上部的量越来越少，熔化相同高度所需热量越来越少，因此相同时间表现出较低的相界面。其中模型1 和模型2 的相界面较其余三者出现了很大不同，模型1和模型2下部也出现大区域的液态相变材料。因此，在下部区域也会出现自然对流，这也是模型1和模型2的熔化速率较快的原因。

5 个模型在14000 s 的相界面较8000 s 的相界面主要差异在于相变材料熔化得更多了，液态相变材料的区域持续扩大，但难熔相变材料的位置并未发生根本变化。模型1 和模型2 的难熔区域仍然为中间区域，模型3、模型4 和模型5 的难熔区域为下部区域。并且下部相变材料的熔化速率越来越慢，这是因为自然对流的存在将高温流体输运到上部区域，热量传递到难熔区域的难度更大。

2.3 平均热阻分析

改变蓄热罐形状对熔化速率产生影响的同时也会对传热流体传递到固态相变材料的难易程度产生影响。为了量化传热流体传递热量到固态难熔区域的阻力，定义了传热平均热阻：

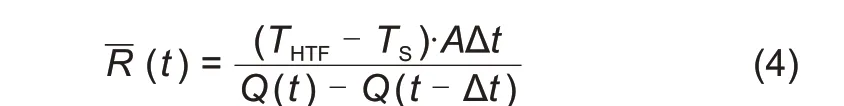
其中，-R(t)为传热平均热阻，THTF与TS分别为换热流体温度与相变材料温度，A为传热面积，Q为传热量。

图6展示了不同模型在整个传热过程中传热热阻随时间的变化趋势，从图中可以看出，模型1、模型2 和模型3 的热阻随着时间推进表现出先上升后下降再上升到最高值的趋势，这主要是因为紧靠铜管的石蜡最先熔化，此时平均传热热阻为铜管导热热阻，为整个过程最小值。待到极薄液态相变材料区域形成时，由于液态区域较小对流传热较弱，加之在固态石蜡和液态石蜡之间液态石蜡的增加导致导热热阻升高，因此总体表现出热阻升高的趋势。随着液态石蜡不断增多，对流传热的加强有利于将热量传递到固体相变材料区域，这减小了从热流体区域传递到固体相变材料区域的热阻。对于模型1 和模型2，由于下部石蜡较少，在相同时刻，下部石蜡平均温度较高，这导致下部石蜡的液体较多，加大了自然对流传递到固态未熔区域的热量，所以平均热阻较模型3会进一步下降。从图中还可以看出，对于每一个模型的热阻在最后时刻都会出现上升的现象，原因有二：其一是石蜡在熔化过程中，固态石蜡的导热系数小于液态石蜡，所以在石蜡不断熔化的过程中，导热热阻是不断增加的；其二，由于石蜡的自然对流，高温液体总会向上流动，而最难熔区域的石蜡处于自然对流波及较弱区域中，所以热量很难传递到难熔区域，这也是导致热阻上升的另一原因。

图6 热阻变化曲线Fig.6 Thermal resistance curves of 5 models

整体来看增加下部区域相变材料的模型4和模型5的阻值比模型1、模型2和模型3要高。这是因为下部石蜡较多，而高温流体多聚集于上部区域，导致热量传递到相变材料的阻力增大。而模型1和模型2的上部相变材料较多，自然对流带动高温流体运动到上部，将热量及时传递到固态区域，表现为平均传热热阻较小。图7 是对图6 传热平均热阻曲线的积分平均，从图中可以看出模型1 到模型5的热阻积分平均值依次增大，而模型1 到模型5 的完全熔化时间依次下降，这完全符合热阻大的模型传热速率慢这一规律。通过对热阻的时间积分平均可以看出采用增大上部区域的相变材料含量可以有效减小平均传热热阻，有利于减少完全熔化时间。

图7 传热平均热阻图Fig.7 Diagram of integral average of thermal resistance

3 结 论

本工作通过数值计算的方法探究了改变蓄热罐形状对竖直壳管式蓄热器换热的影响。设计了一种新型梯形相变蓄热罐，对比分析了具有不同梯度比的5种蓄热罐的完全熔化时间、相界面和平均传热热阻，得出以下结论：

（1）增加上部区域的相变材料有利于将热量及时传递到固态区域，加快整体传热速率。因此，增加上部区域相变材料(即模型1和模型2)的完全熔化时间较基准模型3的完全熔化时间均有缩短，分别减少了39.06%和29.37%。

（2）通过改变蓄热罐形状会对蓄热性能产生影响，模型1 和模型2 的熔化率增长速率较模型3 的熔化率提升速率显著提高，分别高了64.10%和41.59%。

（3）改变蓄热罐形状会影响热流体传递热量到固态区域的难易程度，并且增加上部区域相变材料有利于减小平均传热热阻，增加下部区域的相变材料会增大平均热阻，这与完全熔化时间的大小顺序符合热阻大小与传热快慢的对应关系。