一种基于少量温度传感器的超级电容模组温度监测方法

韦 莉，黄雪林，张婉婷，白欣桐

（同济大学电子与信息工程学院，上海 201800）

超级电容是一种介于电池和传统电容器的高效储能器件，具有功率密度大、循环寿命长、充电速度快以及工作温度相对宽的特点[1]，广泛应用于不间断电源系统[2]、微电网功率波动平抑[3]、城市公交车[4]和轨道交通制动能量回收[5]等诸多领域。在构建规模化储能系统时，由于超级电容单体极限工作电压较低，不能满足大规模储能的需求，故在实际应用中，超级电容常以单体串并联成模组的形式进行工作[6]。

温度对超级电容实际工作性能及其寿命有显著影响。对于超级电容单体，温度降低时由于电解液活性降低，其内阻有所增大；温度升高，超级电容内阻降低[7]，在一定程度上减小了由内阻带来的损耗，原因在于高温提升了超级电容内部电解液的离子迁移率[8]。但也有研究表明，高温将缩短超级电容器的寿命，温度每升高10 ℃，超级电容老化速度将加快1.7～2.5 倍[9-10]，这将大大缩短超级电容及其构成的储能系统的有效服役时间。同时，高温也会加快超级电容电解液的蒸发，电解液的流失将导致性能的持续下降。对于超级电容模组，由于电气参数和散热条件不同，同一模组内各单体在运行时存在温度不一致的情况，温度的不一致性进一步加剧单体电气参数的不一致性，使得模组整体性能进一步劣化[11]。

随着储能系统安全性要求的提高，许多应用场合中要求对超级电容储能模块的每只单体温度进行实时监测，尤其在载运工具等关乎人身财产安全的领域。例如，上海奥威科技开发有限公司2018 年提出的企业标准《船用超级电容器系统》中，要求电容器管理系统对每只单体温度进行显示、报警和保护，并规定温度测量装置的标定准确度不低于0.5 ℃[12]。实时获取温度的分布情况，能够为超级电容热管理系统制定控制策略提供依据，保障储能系统安全稳定运行。

现有获取超级电容模组温度分布的方法主要是传感器监测和仿真预估两种。基于传感器监测方案能够实时准确地获取超级电容单体温度数据，但在超级电容单体数量较多的模组中进行监测需要放置大量温度传感器，所需成本大且不易安装。在超级电容模组温度分布的仿真预估方面，Voicu 等[13]利用CFD(computational fluid dynamics)软件Fluent 6.3 对超级电容模组进行考虑空冷下的数值建模，准确地得到了模组温度分布且与实验数据吻合较好。Frivaldsky 等[14]利用COMSOL 3.5a 软件设计了具有不同复杂程度的超级电容热模型，其改进型电化学双层电容器热模型与精密实验测量结果的相对误差仅为0.08%。西南交通大学戴朝华等[15]在COMSOL Mutiphysics中建立了双电层电容器电化学-热耦合模型，在此基础上研究了不同空间结构下超级电容的热特性，其多物理仿真结果与实验数据的相对误差最大为1.38%。上述基于有限元分析方法对超级电容模组进行的仿真建模虽然能够取得较为精确的温度分布情况，但计算量很大，因此无法用来进行温度的实时预估且不能部署到超级电容管理系统当中。

神经网络是一种对于非线性映射关系有着强大拟合能力的学习框架，目前已有诸多研究利用神经网络对不同应用领域的温度值进行预估的案例：如利用PSO-BP神经网络预估开关柜设备温度[16]、利用LSTM 神经网络进行地铁车站温度预估[17]、基于BP 神经网络对燃煤锅炉温度分布进行预估[18]等，均对相应实测温度数据有良好的拟合度，说明利用神经网络对温度变化进行预估具有一定可行性。

目前，在储能系统研究领域，已有学者使用神经网络方法进行动力电池的温度预估。在单体温度预估方面，Fang 等[19]提出了基于神经网络的镍氢电池单体表面温度预估模型，模型以充电电流、环境温度和充电时间作为输入，用以预估镍氢电池的表面温度，模型的最大绝对误差为1.30 ℃，但未考虑电池放电情形下的温度预估问题，且其预估精度仍有提升空间；Liu 等[20]提出了神经网络与扩展卡尔曼滤波结合方法用于锂离子电池单体的内部温度估计的方法，以电池表面温度、端电压和电流作为神经网络输入，再通过扩展卡尔曼滤波对神经网络输出和集总热模型输出进行数据融合，得到温度预估后验值，最大绝对误差为0.431 ℃，模型精度有赖于集总热模型参数的准确性，在单体成组后，单体间的热量将会相互作用，其单体集总热模型将不再适用；Hasan等[21]基于非线性自回归神经网络建立了锂离子电池的单体温度预估模型，模型输入考虑了电池的充放电电流及环境温度，但最大绝对误差仍大于1 ℃。在模组温度预估方面，Kim 等[22]研究了电动汽车电池组的温度预估问题，其建立的神经网络预估模型考虑了冷却风速、产热率以及1 个模组的实测温度，用以预估剩余5 个模组的温度。模型平均绝对误差为0.19 ℃，最大误差为0.27 ℃。该研究数据来源于Fluent 仿真结果，并未采用实测数据进行验证。神经网络在超级电容温度预估上的应用尚处于起步阶段。Bo等[23]首次将神经网络方法应用于模组温度预估，该研究通过可变等效串联内阻和分子动力学仿真改进了超级电容的电热耦合模型，以模型在COMSOL 中的仿真结果对LSTM神经网络进行训练，实现由电流、冷却风速作为输入预估模组温度，平均绝对误差在0.15 ℃以内，开辟了神经网络用于超级电容模组温度预估的新思路。但该方法依赖详尽的超级电容材料属性和内部结构参数，相关参数在商用超级电容模组中较难获取。

针对现有超级电容模组温度监测手段的不足，本工作的创新性在于提出了基于神经网络的超级电容模组温度分布预估模型，模型输入少量单体温度以及电压电流等数据，能够实现模组内剩余单体温度的准确预估，大大减少了温度传感器的使用。同时，本工作研究了不同单体组合作为输入以及电流、电压、风速等因素对温度预估的影响，据此对温度预估模型的输入特征进行取舍，提高了模型预估温度的准确性。

本工作内容如下：首先进行了某型号商用超级电容模组温度测试实验，获取了不同冷却风速下超级电容模组的温度数据；其次，研究了超级电容模组温度分布情况，发现模组内各单体温度具有强相关性；基于该特征，提出超级电容模组温度预估模型的基本架构；通过模型预训练，选取了特定单体组合和输入特征作为模型输入，使模型能够更好地学习模组温度的数据特征；最后，通过测试数据集验证了模型的预估效果。

1 超级电容模组温度测试实验

为了研究超级电容模组温度分布和变化规律，本工作进行了超级电容模组在不同冷却风速下的多段恒流充放电实验，获取了超级电容模组内各单体温度数据，为进行超级电容模组温度分布特征分析和建立模组温度预估模型作了数据准备。

实验对象为某型号商用混合型超级电容12 只单体串联组成的模组，单体的性能指标如表1 所示。实验所用模组的实物和单体排布方式分别如图1(a)和图1(b)所示，单体以12×1形式排列，单体上下间隔2 mm，单体尺寸17.0 cm×8.0 cm×1.2 cm(长×宽×高)。由上至下，单体对应标号为#1至#12。

图1 受试超级电容模组实物图及排布示意图Fig.1 The physical map and layout diagram of the tested supercapacitor module

表1 某混合型超级电容器单体技术指标Table 1 Technical indicators of a hybrid supercapacitor cell

在进行超级电容模组温度测试实验的过程中，为了不损坏超级电容本身，对于超级电容单体和模组的充放电均应使其电压保持在额定工作电压区间内。

超级电容测试平台如图2所示，主要由电源系统、DC/DC 变换器、超级电容模组、负载电阻、传感器、信号采集与调理电路和数据处理终端组成。在充电过程中，由电源系统供能，电能经过DC/DC 变换器后以预设电流波形给超级电容模组进行充电；在放电过程中，首先切换机械开关改变主电路，DC/DC 变换器与电源系统断开转接负载电阻，由超级电容模组经过DC/DC 变换器对负载电阻进行预设电流波形的放电。实验过程中，采集的电压、电流和温度信号经传感器、信号采集与调理电路后送至数据处理终端进行显示和计算。

实验中的多段恒流充电波形如图3所示，充电过程历经1 C(1 C为1电流倍率即15 A)、2 C、3 C、4 C、5 C、6 C恒流脉冲充电，脉冲宽度20 s，间隔30 s，而后以5 C进行75 s充电；重复上述充电过程直至电压接近上限，而后以4 C、3 C、2 C、1 C 逐次降低的电流等级充电以实现满充。放电过程使用的电流波形与充电过程一致，仅电流方向发生改变。为获取冷却条件对超级电容模组温度的影响，模组的多段恒流充放电是在无风以及风速分别为5.0、6.0、7.5、9.8 m/s的条件下进行。

图3 多段恒流充电波形Fig.3 Multi-stage constant current charging profile

单体温度通过在每个单体上表面中部放置一个PT1000 铂电阻温度传感器进行测量，另在台架无风处安置传感器以测量环境温度，通过安捷伦34901 A数据采集模块进行数据采集，采样频率为0.5 Hz。1路电流信号和12路电压信号通过NΙ测控平台进行采集，采样频率为200 Hz。风速记录的是风扇出风口的风速，由风速测量仪测得。

以风速9.8 m/s为例，图4(a)、4(b)、4(c)分别为该冷却条件下电流I、电压U、温度T的测量结果，为方便采样数据时间戳对标和后续处理，对电流电压信号进行了数据重采样，处理后的数据采样频率与温度数据一致，为0.5 Hz。单体电压一致性较好，为了便于显示仅给出1 号单体电压U1。T1～T12分别表示#1～#12单体的电压温度，Ta为环境温度。

图4 风速为9.8 m/s时的测试结果Fig.4 Test results when the wind speed was 9.8 m/s

从实验测得的温度变化数据可以看出，超级电容模组当中，所有单体的温度均随着充放电电流波动变化，大电流时温度上升较快；小电流或无电流时，由于冷却温度出现下降，说明温度变化与电流大小具有相关性。模组当中不同单体的温度变化趋势具有明显的同步性，这对于构建温度预估模型是有利的。

2 超级电容模组温度分布预估

2.1 温度数据的相关性分析

图4(c)给出了多段恒流充放电过程中，单体温度随时间变化的曲线，表征单体的每条曲线的增长趋势具有明显的同步性。从单体温度的相对大小关系上，可以大致将单体温度按大小分为3组：较低的T1 和T8 单体温度，较高T2、T4、T5、T10、T11、T12 单体温度以及剩余处在中间温度区域的单体温度T3、T6、T7、T9。

进一步地，分析多段恒流充放电过程中单体温度变化的相关性，以Pearson 相关系数作为衡量指标：

相关系数rxy表征序列x和序列y的相关性，L为序列总长度，rxy∈[-1，1]，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。以9.8 m/s 风速下多段恒流充放电温度变化数据为例，计算T1～T12温度变化数据序列两两之间的相关系数，得到如图5所示的相关系数矩阵。

图5 风速为9.8 m/s时的温度数据相关系数矩阵Fig.5 The correlation coefficient matrix of the temperature data when the wind speed was 9.8 m/s

从相关系数矩阵中可以看出，单体相关系数均在0.97以上，说明不同空间上的超级电容单体的温度具有很强的相关性，可以利用这一相关性构建模组温度预估模型。另外，考虑到温度随电流波形出现波动，在构建模组的温度预估模型时，可以考虑将充放电电流作为考量因素之一，体现出电流对于模组温度表现的影响。

2.2 神经网络的基本原理

神经网络是一种由相互连接的人工神经元构建的机器学习算法框架。神经网络的主要组成元素是网络中数量众多的神经元(图6)和连接于神经元间的权值(和偏置)，连接权值表征相邻两层神经元之间的联系紧密程度，而神经元负责对接收到的输入进行激活响应[24]。神经网络通过一定的学习过程，对网络输入特征进行学习，能够在一定误差范围内取得输入输出之间的非线性映射关系。

图6 神经网络的基本单位：神经元Fig.6 The basic unit of a neural network:the neuron

神经网络的学习过程主要分为前向传播和反向传播两个过程[25]。在前向传播过程中，各层神经元对前一层的输出做线性加权并进行非线性激活运算，如式(2)和式(3)所示：

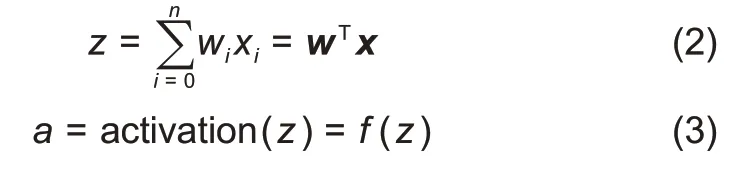
输入数据经过层层计算后与预期输出进行误差计算，得出本次计算误差；在反向传播过程中，会依次计算误差相对于网络参数的偏导数，依照梯度下降原则对网络参数进行修正，使得网络计算误差具有减小的趋势，式(4)为参数更新的基本公式，α表示学习率。

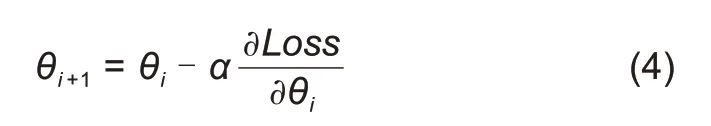
神经网络中的众多参数和激活函数赋予其优异的非线性函数拟合能力，通用近似定理指出，采用一定层数和一定数量神经元的神经网络可以训练出较为接近输入输出关系的预估函数[26]。故从理论上来说，利用神经网络这个具有强大拟合能力的“黑箱”来构建预估模型是可行的。

2.3 温度预估模型的建立

基于神经网络构建超级电容模组温度预估模型主要分为以下过程：确定网络架构以及选择优化算法。

2.3.1 确定网络架构

所考量的预估模型输入为12 只单体温度、电流、单体电压数据以及环境温度、冷却风速等外在因素，需要一部分单体温度数据作为输入，预估剩余单体温度。为确定模型最佳输入单体温度组合以及输入特征，本工作首先列举不同的可能输入组合，通过不同单体组合、不同特征在同一基础预训练模型上的表现来对其进行筛选，以提高模型准确性。

初步构建的神经网络模型代号为NNv1，其输入特征、网络结构、预估对象如表2 所示，其中，为使网络能够学习温度的缓慢变化过程，输入特征还包含单体温度的延迟序列Tink-1，神经网络隐藏层神经元数量取为30，N为测试数据长度，n为输入单体数量。

表2 神经网络NNv1的基本架构Table 2 The basic architecture of the neural network NNv1

考虑到单体温度大致分为3个温度分区，同一分区的单体温度特征相近，故决定同一温度分区至多取一个单体温度数据作为输入，由此根据2.1 节的温度分组，可以列举出104种输入单体组合：单体数量n=1 时有12 种，n=2 时有44 种，n=3 时有48种。依据表2所构建的神经网络对该104种单体组合进行训练和误差对比，不同组合对应的误差情况如图7所示，衡量指标为温度序列的平均绝对误差(MAE，mean absolute error)。

图7 不同输入单体组合下进行预训练的MAEFig.7 Pre-trained MAE with different combinations of input cells

图7 的预训练结果表明：n=1 时，模型预估误差介于[0.1275，0.2193]；n=2 时，模型预估误差介于[0.0955，0.3995]；n=3 时，模型预估误差介于[0.0787，0.4469]。可以看出，随着输入单体数量的增多，模型预估误差呈现减小的趋势，这是因为模型能够从输入端获取更多的信息来构建输入输出端之间的非线性关系，从而降低误差。为取得较好的预估效果、节省传感器数量和简化模型，不考虑n＞3的情形，因而选取n=3中预训练结果最好的单体组合(T4，T6，T8)作为模型输入组合，其预训练MAE为0.0787 ℃，用于预测剩余模组内剩余单体温度即T1、T2、T3、T5、T7、T9、T10、T11、T12。

进一步地，为研究表2 建立的神经网络模型NNv1 中各个输入特征对于预估效果的影响，基于NNv1 网络，本工作尝试将不同输入移除，通过模型的预训练效果评价不同特征对模型性能的影响，并对网络特征的取舍提供参考。为使模型不至于过拟合，训练过程在误差降低幅度小于前一次训练误差的10%时停止训练，模型训练使用Levenberg-Marquardt算法。

由表3可以看出，分别移除电流、风速、输入单体温度、环境温度时，模型的预训练误差不同程度地增大，尤其输入单体温度、电流、环境温度对模型性能影响较大，说明初始模型NNv1的输入特征基本是合理的；模型在移除单体电压这一输入后性能有少许改善，说明电压与温度变化相关性不强，电压波动并不利于温度预估，在后续模型改善中考虑将电压因素排除在外，即采用NNv3的网络架构。

表3 移除特定输入特征后的预训练误差Table 3 Pre-training error after removing specific input features

神经网络相关理论并没有关于网络层数和神经元数量的确定法则，同时这两类结构参数并不能通过训练得到学习，在实际应用中更多的是依赖神经网络使用者对于特定问题的经验性判断。前文采用的具有30 个隐藏神经元的单层神经网络具有较好的拟合效果，可以沿用。

2.3.2 选择训练算法

本工作选取了几种常用的神经网络训练算法：动量法[27]、拟牛顿法和学习率可变的BP 算法对选用的网络模型NNv3进行训练，通过在预训练模型上的MAE 来与Levenberg-Marquardt 算法进行对比。如表4 所示，Levenberg-Marquardt 算法得到了最小的预估误差，其他算法不同程度地增大了预估误差，其中动量法由于算法不收敛误差始终在1 ℃以上，MAE 为1.7444 ℃。由此，可以将Levenberg-Marquardt算法确定为本工作温度预估模型的训练算法。

表4 网络模型NNv3在不同训练算法下的误差Table 4 Error of network model NNv3 under different training algorithms

2.4 温度预估模型验证

本工作针对2.3 节选用的温度预估模型架构NNv3 和训练算法Levenberg-Marquardt，进行了如下验证工作：选取风速为7.5 m/s 的温度测试数据作为模型验证的测试集数据，其余风速以及无风条件下的测试结果作为训练集，训练集与测试集的比例为5∶1，这种划分数据集的方法被称为留出法[28]。使用NNv3 模型基于Levenberg-Marquardt算法对划分的训练集数据进行学习，并通过训练好的神经网络模型对留出法取出的测试集进行预估，得到模型在测试集数据上的预估性能指标。模型训练时设定的学习率为0.005。

最终，模型在测试集数据上得到的温度预估拟合情况如图8。其中，实线为单体温度实际值，虚线为单体温度对应的预估值。

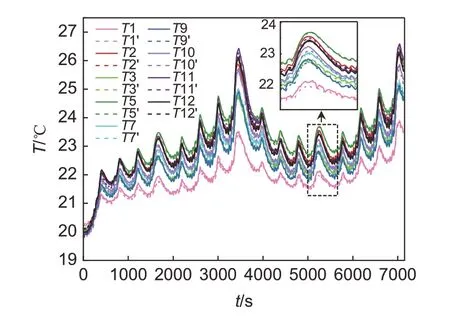
图8 测试集温度及其预估温度Fig.8 Temperature in test dataset and the estimation

模型在各个单体上预估的最大绝对误差和平均绝对误差如表5 所示，总体MAE 为0.06 ℃，最大绝对误差在0.3 ℃以内，模型在测试集上的预估效果是比较准确的，符合超级电容储能系统对于温度监测精度的要求。

表5 测试集预估的绝对误差Table 5 Absolute error of estimation in the test dataset

3 结果与讨论

本工作构建的基于神经网络的超级电容模组温度预估模型取得了总体平均绝对误差为0.06 ℃的预估效果，针对算法本身的性能并与传统传感器监测方案比较，可从以下三个方面对温度预估模型进行评价：

（1）准确性：基于神经网络的超级电容模组温度预估模型对于测试集温度进行了较为准确的预估，总体平均绝对误差为0.06 ℃，预估误差基本满足实际超级电容管理系统要求，如在船用超级电容管理系统中，对于温度测量的标定准确度要求不低于0.5 ℃，而本工作提出的模型在预估单体上的最大绝对误差在0.3 ℃以内，完全符合要求。

（2）实用性：本工作构建的模组温度预估模型基于少量单体温度结合算法进行温度预估，相比于传感器监测方案更加实用、灵活：一是温度预估算法在执行预估阶段占用的计算资源很小，可以方便地部署在原有超级电容管理系统中；二是温度预估算法依赖于大量实验数据，可以定期利用测试数据对模型进行离线训练后重新部署到系统中，实现算法的优化。

（3）经济性：用温度预估算法模型计算结果代替部分温度传感器测量数据，可以减少温度传感器的使用，不仅为超级电容模组集成节省了空间，同时降低了温度传感器购置成本：实验中用到了PT1000 系列铂电阻温度传感器，其市场单价在15 元左右，使用算法预估温度可以将温度传感器数量从12个减少至3个，而算法模型本身部署在原有计算硬件中，并不会带来额外开销。

4 结 论

对于超级电容模组温度监测问题，传统的传感器监测方案存在成本过高且难以安装的不足。本工作针对这一问题，分析了超级电容模组不同冷却风速下的多段恒流充放电温度数据，得到了模组中单体温度的分布规律，建立了一个以3 路单体温度、电流测试数据、冷却风速、环境温度作为输入的BP 神经网络，预估模组内剩余单体温度。结果表明，该模型取得了较为准确的预估效果，总体平均绝对误差约为0.06 ℃，最大绝对误差在0.3 ℃以内。相较于传感器监测方案，模型预估方法在保证准确度的情况下，节省了大量温度传感器的购置成本且避免了安装传感器带来的困扰，具有经济性和实用性上的优势，也为未来超级电容管理系统温度监测部分的构建提供新思路。