锂离子电池参数辨识及荷电状态的估算

刘志聪，张彦会

（广西科技大学机械与汽车工程学院，广西 柳州 545616）

近年来，由于环境问题日益突出和石油资源的逐渐匮乏，新能源电动汽车得到了越来越多的关注。锂离子电池作为电动汽车的主要储能部件也逐渐成为众多学者研究的热点问题，锂离子电池的荷电状态(state of charge，SOC)估算精度一直以来都是制约电动汽车发展的重要因素。SOC 反映的是电池剩余可用容量与电池最大可用容量的比值，精确的SOC值一方面对整个电池管理系统(battery management system，BMS)具有重要意义，BMS通过反馈的SOC 值来实现对电池的调节控制，另一方面，对于驾驶而言精确的SOC 值可以帮助驾驶人员合理安排出行避免出现电量里程焦虑。

为了提高对电池SOC 的估算精度，国内外学者进行了大量的研究。在估算方法方面，既有传统的安时积分法和开路电压法，又有基于模型的估算方法和基于机器学习等估算方法。安时积分法和开路电压法由于受到传感器测量误差和电池静置问题的限制很难单独应用于电池SOC 的估算，而基于机器学习的估算方法需要对电池进行大量的实验和对数据进行训练，工作量比较巨大[1]。基于电池模型的估算方法能够克服传统方法和机器学习方法的一些局限性，成为了目前最为普遍的电池SOC 估算方法。目前，电化学模型和等效电路模型是最常见的电池建模方法，其中电化学模型中涉及大量电池内部化学反应，整个建模过程中存在着许多复杂的方程式且要求专业的化学知识，对建模者要求较高，而等效电路模型则是利用简单的电路元件的组合来描述电池工作时的电压电流变化关系，模型中具有清晰简单的函数关系式，是大部分学者都选择的建模方式[2]。参数辨识也是电池SOC估算中的重要环节，在完成电池等效模型建立后，需要对模型中的各参数进行辨识确定其参数值，参数辨识方法主要有基于脉冲放电实验下的离线参数辨识，但是离线参数辨识的模型参数是固定的，在一些复杂的电池工况下，离线辨识得到的参数值不能准确反映电池当前工作下的电池变化情况，所以有学者提出了在线参数辨识方法。递推最小二乘法是常用的在线参数辨识方法，但是随着递推的进行会因数据饱和的现象造成辨识出现误差，于是文献[3]通过带遗忘因子的最小二乘法对模型进行在线参数辨识来解决数据饱和等问题，文献[4]利用自适应遗忘因子来解决在递推过程中遗忘因子固定不变的问题能更好地达到辨识效果。

在估算算法方面经常利用卡尔曼滤波(Kalman filter，KF)算法来实现对电池SOC的估算，但是传统的KF算法解决的是一般的线性问题，而电池在工作时是一个高度的非线性系统，为此有学者在KF的算法基础上提出采用扩展卡尔曼滤波(extended Kalman filter，EKF)算法来处理非线性的电池系统，通过对函数进行泰勒级数展开，取其一次项来近似非线性系统，该方法的缺点是在处理较强的非线性系统时存在着较大的系统误差，且系统噪声被假定为相互独立的高斯白噪声。EKF中固定的过程噪声和测量噪声会降低系统的估算精度，针对这个问题文献[5]中提出了新的自适应卡尔曼滤波(adaptive extended Kalman filter，AEKF)算法，将自适应更新协方差矩阵的特性添加到EKF中，让系统的噪声特性能根据估计结果而自适应更新从而提高SOC 的估算精度。此外，为了进一步解决系统的非线性所带来的误差问题，文献[6]在EKF 算法的基础上提出了sigma-point 卡尔曼滤波(sigmapoint Kalman filter，SPKF)方法来估计非线性系统的状态。

建立一个准确的电池模型和实现对模型参数的精确辨识是实现对电池SOC 估算的基本前提，本工作采用能表征电池电化学极化和浓度差极化的二阶RC 等效电路模型来实现对电池的建模，提高了电池的建模精度；并分别利用了离线和在线参数辨识方法来对等效电路中的参数进行辨识，两种参数辨识方法都能满足模型精度要求。最后在FUDS和UDDS 工况下验证了EKF 算法对电池SOC 估算的有效性，并证明了在相同的工况下在线参数辨识模型的SOC估算精度要高于离线参数辨识模型。

1 理论分析

1.1 电池等效电路模型的建立

目前，比较主流的电池模型有电化学模型、等效电路模型和黑盒模型等，本工作采用的是等效电路模型。等效电路模型利用电器元件组成的回路来模拟电池工作时的电流与电压变化，其简单的函数关系式和明显的电气特性受到广大学者的关注。其中包含了Rint 模型、PNGV 模型、GNL 模型和RC回路模型等[7]，每个模型都有自己的优缺点。本工作采用了拥有两个RC 回路和一个欧姆内阻的二阶RC 模型来模拟电池的动态变化特性，原理如图1所示。两个RC 回路分别表示了电池的电化学极化和浓度差极化，欧姆内阻表示了电池的内阻特性，该模型相较于其他模型具有更高的模拟精度，参数辨识也较其他模型更为方便准确。

图1 二阶RC等效电路模型Fig.1 2RC equivalent circuit model

图1中，Uoc表示电池的开路电压；Ut表示电池的端电压；I表示电池工作时的充放电电流；R0表示电池的欧姆内阻；R1和R2表示电池的极化电阻；C1和C2表示电池的极化电容。运用基尔霍夫定律可以得到回路的函数关系式：

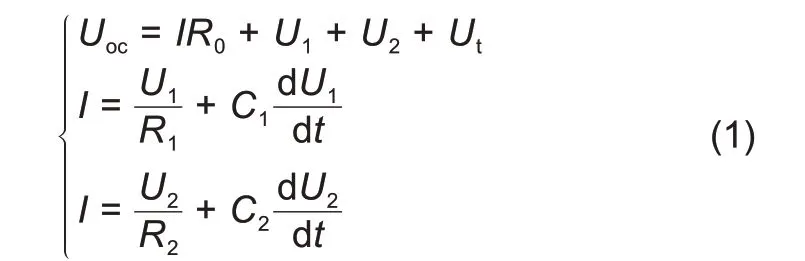
式中，U1和U2为两个RC 回路的电压；Uoc可以由电池SOC确定；I和Ut为电池工作时的电流和电压，可由传感器测得。

1.2 基于实验的参数离线辨识方法

在等效电路中I和Ut可由传感器测得，Uoc是一个关于SOC 的函数，需要对剩下的R0、R1、R2、C1、C2进行辨识，确定其在电池工作时的值。目前比较常用的离线辨识方法是对电池进行复合脉冲功率性能测试(the hybrid pulse power characterization，HPPC)。

为了验证所提出的SOC 估算方法的有效性，本工作采用来自马里兰大学的实验室数据进行仿真。使用的测试设备包括一套控制和记录电池充电和放电过程的Arbin BT200电池测试系统，以及一个控制电池环境温度的热室。本工作以ΙNR18650-20R 锂离子电池的测试数据为例来验证SOC 估算方法的有效性。电池的规格见表1。

表1 电池规格Table 1 battery specification

在实验中对电池进行恒流脉冲放电实验，实验步骤为[8]：

（1）用恒流恒压的充电方式将电池充满即

SOC=100%。

（2）以0.5 C(1 A)对电池进行放电直至电池SOC减少10%。

（3）放电结束后将电池静置2 h。

（4）重复步骤(2)、(3)直到电池SOC=0或者达到放电截止电压时结束实验。

实验结果如图2所示。

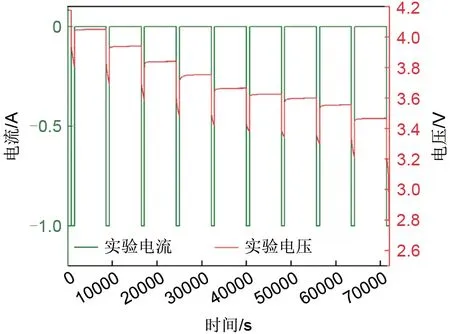
图2 恒流脉冲放电电流电压的变化Fig.2 Constant current pulse discharge current voltage change

图3为锂离子电池在一个放电过程中电压电流变化曲线，记脉冲放电开始和结束时刻分别为A点和C点。

图3 脉冲放电局部放大图Fig.3 Partial enlargement of pulse discharge

从图3中可以看出在电池放电过程中有两个比较特殊的阶段，即B-C和D-E两个阶段。产生这两个特殊阶段的主要原因是电池内部存在极化内阻，由于极化内阻的存在导致电压出现“迟滞效应”。在等效电路模型中用两个RC 回路来模拟电池的极化内阻，所以可以通过B-C和D-E两个阶段的电压来辨识出等效电路中RC回路中的模型参数。而A-B和C-D两个阶段电池的电压发生突变，这是由电池欧姆内阻R0造成的，利用这两个阶段可以完成对R0的辨识[9]。

由欧姆定律可知：

式中，UA、UB、UC、UD分别为A、B、C、D点的电压；I为放电电流。由上式可以准确辨识出不同SOC时刻下的R0值。

B-C阶段为放电刚开始时电池电压缓慢下降的过程，此阶段依然有电流流过回路对应的RC 回路中的零状态响应阶段：

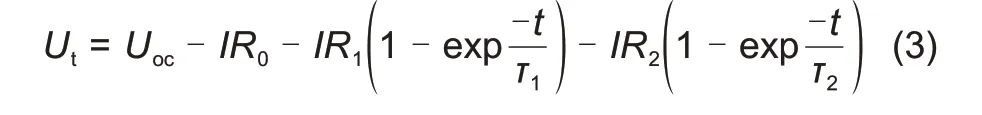
式中，τ1=R1C1，τ2=R2C2分别为两个RC 回路的时间常数；Uoc、I、R0为已知。在通过Matlab中的Cftool 拟合工具箱对B-C的电压进行拟合。将R1、R2、τ1、τ2作为待定系数进行拟合，自定义拟合函数：

通过对B-C的电压进行拟合可以得到系数b、d的值，再由欧姆定律便可以求出不同SOC时刻下的R1、R2。

D-E阶段为放电结束时电池电压缓慢上升的过程，此阶段没有电流流过回路对应的RC 回路中的零输入响应阶段：

这个阶段拟合出系数c和e，再利用公式τ1=R1C1、τ2=R2C2便可以求出不同SOC时刻下的C1、C2。

1.3 基于带遗忘因子的递推最小二乘法的参数在线辨识

电池在实际工作时是一个高度非线性的时变系统，而上述的离线参数辨识方法并不能解决电池在工作时参数与实际情况不匹配的问题。为了提高等效电路模型的精度，需要引入在线参数辨识方法来解决电池参数在时刻发生变化的问题。在线辨识是在电池实际工作中通过采集电池的各项数据如电流电压等，再根据等效电路模型解析出各参数的数学关系式，最后根据算法求解出电池在当前时刻各参数的具体数值。在线辨识的最大优点是各参数随电池工作的时间变化而变化，能够真实反映出在不同时刻下电池的参数，能够在一定程度上提高模型的精度。本工作采用带遗忘因子的递推最小二乘法来实现对参数的在线辨识。

递推最小二乘法作为系统识别的典型方法之一，其基本原理就是根据当前时刻的输入值和上一时刻的估计值来进行修正从而获得当前时刻估计值的，递推最小二乘法的迭代公式如下：

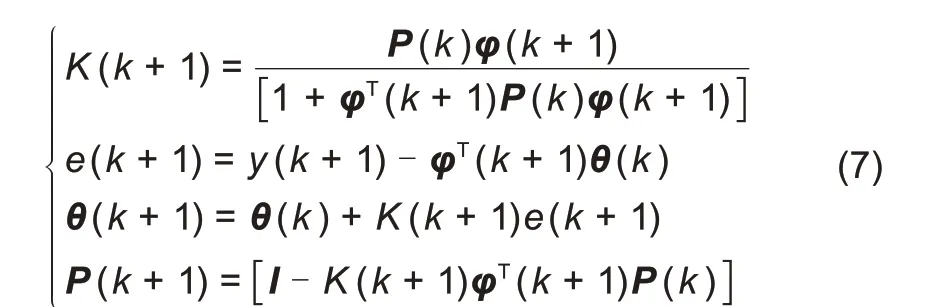
式中，K为系统的增益；e为系统的预测误差；y为系统的观测值；φ为观测向量；P为误差协方差矩阵；θ为带辨识参数矩阵；k+1 为在k+1 时系统的值。

但是随着递推算法的不断进行，算法会出现数据饱和的现象，从而影响算法的估算精度，为了解决这个问题在递推算法中引入了遗忘因子λ，通过λ来调整旧数据在递推过程中的比重，对旧数据采取逐渐遗忘，从而提高估算精度。λ取值范围为0.9～1；带遗忘因子的递推最小二乘法(forgetting factor recursive least square，FFRLS)的迭代公式如下[10]：

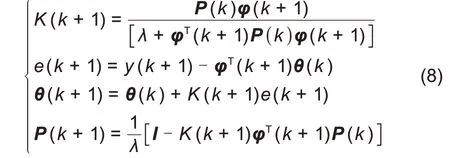
根据FFRLS 算法原理，需要对式(1)进行拉普拉斯变换，可以得到电池在频域下的传递函数：

为确保系统离散化前后一致，本工作采用Z变换对系统进行离散化：

由式(17)可以得到系统的差分方程：

再根据式(12)和式(21)可以求出R0、R1、R2、C1、C2的值：

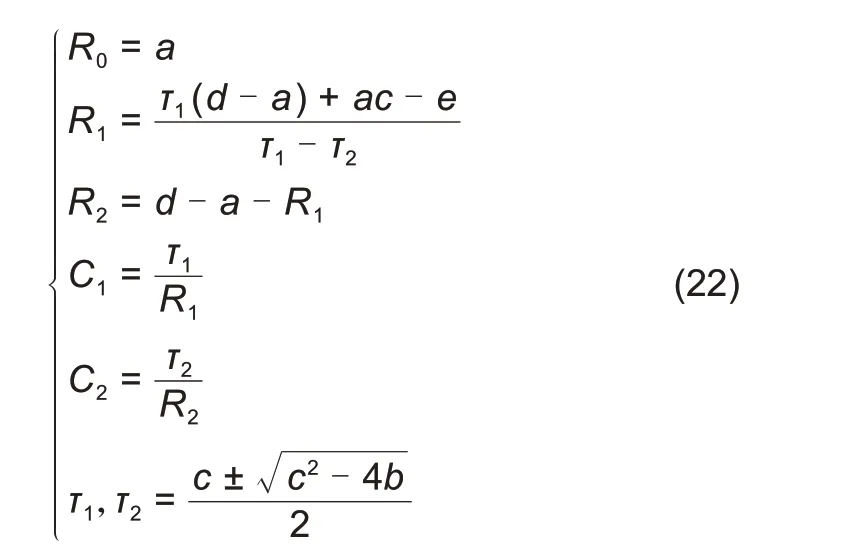
采用FFRLS算法根据式(22)便可以对系统中的各项参数进行辨识。

1.4 电池SOC估算

本工作采用卡尔曼滤波(Kalman filter，KF)算法来实现电池SOC的估算。但是KF解决的数学模型一般都是线性的，而电池是一个高度非线性的数学模型，为解决非线性模型有人提出了扩展卡尔曼滤波(extended Kalman filter，EKF)算法。其基本思想是对非线性系统的状态方程式进行泰勒级数展开，取一阶或二阶级数进行近似线性化[11]。对非线性系统有：

式中，x、u分别为系统的状态变量和输入量；y为系统的输出量；ω、v分别为系统的过程噪声和观测噪声，都是均值为0 且相互独立的高斯白噪声；f(xk-1,uk-1)和h(xk-1,uk-1)分别为系统的状态方程和观测方程；k为迭代时刻。

将式(23)进行泰勒级数展开并近似有：

为了实现利用EKF算法对电池SOC进行估算，需要根据等效电路模型数学关系式找出电池系统对应的观测方程、状态方程和输出方程。

把系统的SOC、U1、U2作为系统的状态变量可以得到：

在得到电池模型的各参数和状态空间方程后，根据EKF算法步骤，便可以实现对电池SOC的估算。

2 实验结果与分析

2.1 离线参数辨识结果分析

在进行参数辨识前，需要得到电池的开路电压Uoc，Uoc值跟电池SOC 值具有很强的函数映射关系，得到准确的Uoc对后续准确估算SOC具有重要意义。

Uoc定义为电池在充放电结束后电池在得到充分静置后电池两端稳定的电压，通过图2所示的实验结果取静置2 h后的实验电压作为电池的Uoc，可以得到在不同SOC时刻下相对应的Uoc，见表2。在得到不同SOC时刻下的Uoc后，利用Matlab中的Cftool拟合工具箱对实验数据进行拟合。拟合公式如下，拟合结果如图4所示。

图4 SOC-OCV拟合曲线Fig.4 Fit the graph of SOC-OCV

表2 不同SOC下的UocTable 2 Uoc under different SOC

f(x)=p1x7+p2x6+p3x5+p4x4+p5x3+p6x2+p7x+p8(39)

式中，f(x)为不同SOC 下的Uoc；x为SOC 值；p为拟合系数。

在对Uoc进行拟合后，根据图3 利用式(2)、式(3)、式(5)可以完成对模型参数的离线辨识，整个实验的参数辨识结果见表3。

表3 离线参数辨识结果Table 3 Offline parameter identification results

在完成系统参数辨识以后，为了验证等效电路模型和参数辨识结果的正确性，将辨识好的参数加载到等效电路模型中，对等效电路模型加载实验的工况电流，对比仿真端电压和实验端电压误差，仿真结果如图5所示，仿真误差如图6所示。

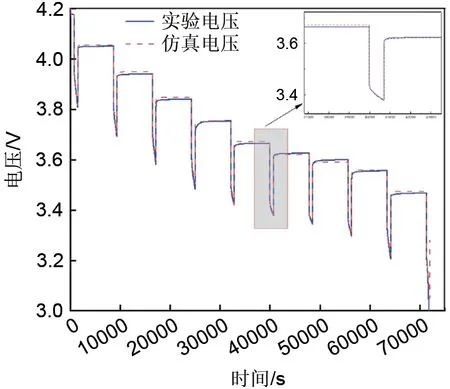
图5 实验端电压与仿真端电压对比Fig.5 Contrast diagram of experimental terminal voltage and simulation terminal voltage

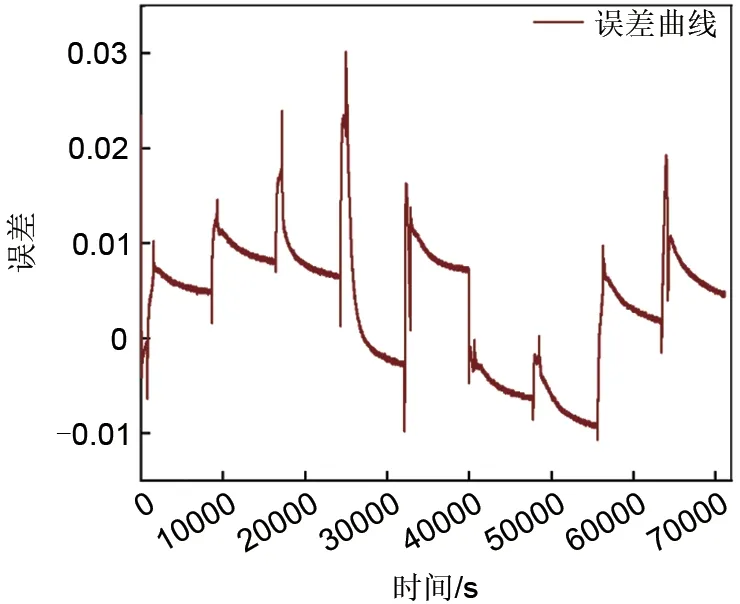
图6 实验端电压与仿真端电压误差曲线Fig.6 Experimental terminal voltage and simulation terminal voltage error curve

由仿真结果可知，仿真电压与实验电压的最大误差只有0.0301 V，平均误差仅为0.0037 V，均方根误差(root mean squared error，RMSE)为0.75%，证明本工作所建立的等效电路模型和参数离线辨识结果准确有效。

2.2 参数在线辨识结果与分析

在进行电池模型参数在线辨识时要求电流激励为持续激励，本工作采用FUDS工况对电池进行测试来验证在线参数辨识的可行性。实验数据同样是采用马里兰大学的实验室数据，数据的初始SOC值为80%。将FUDS工况下的电压和电流作为FFRLS算法的输入输出，通过FFRLS 算法便能准确辨识出在电池工作时等效电路的各模型的参数。辨识结果如图7～图11所示。

图7 R0参数辨识结果Fig.7 R0 parameter identification results

图8 R1参数辨识结果Fig.8 R1 parameter identification results

图9 R2参数辨识结果Fig.9 R2 parameter identification results

图10 C1参数辨识结果Fig.10 C1 parameter identification results

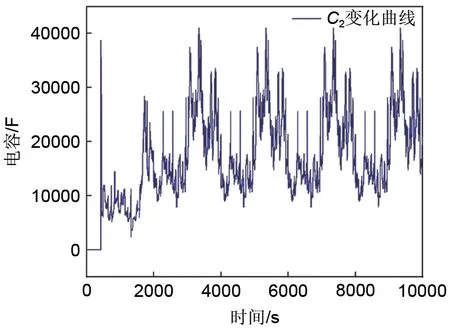
图11 C2参数辨识结果Fig.11 C2 parameter identification results

为了验证在线参数辨识结果的有效性，在等效电路模型中加载FUDS工况的工作电流，将各参数辨识结果输入到模型中，对比仿真端电压和实验端电压误差，仿真结果如图12 所示，仿真误差如图13所示。

图12 FUDS工况下端电压对比曲线Fig.12 Terminal voltage comparison curve under FUDS condition

图13 FUDS工况下端电压误差曲线Fig.13 Terminal voltage error curve under FUDS condition

通过实验结果和仿真结果误差对比可知，在刚开始时由于各参数初值设置得不够准确，误差比较大，但是随着算法的进行误差也在逐渐减小，由图11 可知在1000 s 以后最大电压误差仅为0.1 V，平均误差仅为0.011 V，RMSE为1.8%。通过实验结果与仿真结果的对比分析验证了参数在线辨识的有效性，提高了电池等效电路模型的精度，为后续实现对电池SOC准确估算提供了较大帮助。

2.3 EKF估算SOC结果与分析

为验证EKF 算法估算SOC 的有效性和不同参数辨识模型的估算精度，同样在FUDS和UDDS工况下进行仿真验证，分别对离线参数辨识模型和在线参数辨识模型加载相同的FUDS和UDDS工况电流来验证SOC估算的准确性，估算结果如图14和图15所示。

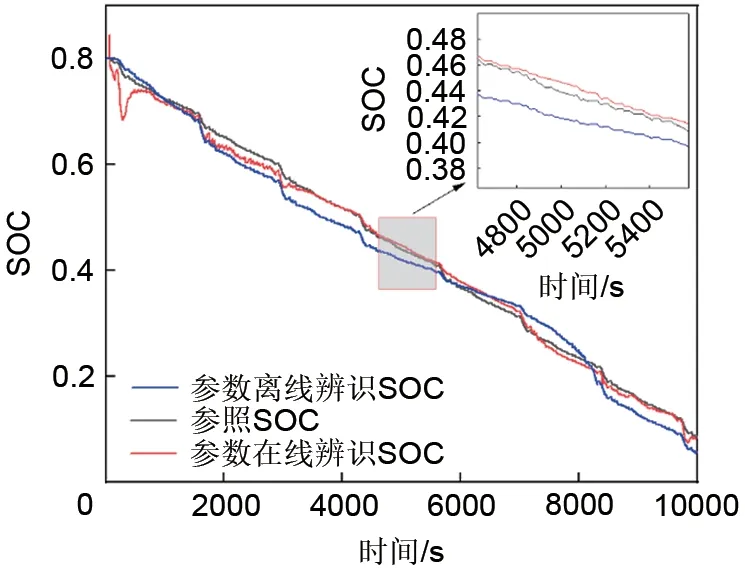
图14 FUDS工况下EKF算法估算SOC结果Fig.14 EKF algorithm to estimate SOC result graph under FUDS

图15 UDDS工况下EKF算法估算SOC结果Fig.15 EKF algorithm to estimate SOC result graph under UDDS

实验结果表明，在初始SOC为0.8的FUDS工况下，离线参数辨识模型的SOC 估算最大误差为3.8%，平均误差为1.2%，RMSE为2.4%，在线参数辨识模型的SOC估算最大误差为2.4%，平均误差为0.5%，RMSE 为1.3%。在初始SOC 为0.8 的UDDS工况下，离线参数辨识模型的SOC估算最大误差为3.2%，平均误差为1.9%，RMSE 为2.1%，在线参数辨识模型下的SOC 估算算法稳定后最大误差为2.1%，平均误差为1.0%，RMSE 为1.5%。对两个模型分别加载FUDS和UDDS工况运用EKF算法均能实现对SOC 的准确估算，但是在电流变化复杂的工况下，在线参数辨识模型能够更好地实现对SOC的估算。

3 结 论

本工作建立了二阶RC 等效电路模型来模拟电池的电气特性，对等效电路模型实现了准确的离线参数辨识和在线参数辨识，在MATLAB软件中对电池端电压进行仿真，验证了参数辨识的有效性。在完成建模与参数辨识后，运用EKF 算法对电池SOC 进行估算，仿真结果表明，在环境温度为25 ℃的FUDS和UDDS的工况下SOC估算平均误差均在2.5%以下验证了EKF 算法对电池SOC 估算的有效性。并且在两个工况下在线参数辨识模型的SOC 估算平均误差和RMSE 都要比离线参数辨识模型有所降低，表明在线参数辨识方法在复杂的电池工况下对SOC 估算更具优势。虽然本工作实现了对电池SOC 估算，但是估算过程是在恒温下进行的，并没有考虑到外界温度对SOC 估算的影响，同时在运用EKF 算法进行估算时，由于EKF 算法中的噪声是固定的，忽略了噪声变化带来的估算误差，需要在后续的研究中不断改善。