高速机动目标长时间相参积累和参数估计算法研究
杨宇超, 方 明, 赵晨帆, 王玥琪, 方 刚
(上海航天电子技术研究所, 上海 201109)
0 引 言
近十多年来,随着航天技术的发展,各种具有高速高机动性的目标例如超高声速导弹、战斗机、无人飞行器等层出不穷。同时,隐身技术的大量运用也使得雷达回波信号微弱,降低了目标的积累增益[1-2]。众所周知,增加雷达的照射时长是提高信噪比的有效方法。然而,随着积累时间的增加,距离走动与多普勒走动效应也会随之出现。传统的积累算法动目标检测(moving target detection, MTD)[3]的性能受到目标在距离单元内驻留时间的限制,难以有效提高高速高机动目标的积累增益。因此,研究具有距离校正与多普勒校正能力的长时间积累算法具有重大的意义。
近几年来,随着研究的深入,长时间积累算法得到了快速发展。相关的研究工作按照算法原理的不同可以大致分为以下3类。第1类算法为基于拉东变换的长时间积累算法。其典型算法有改进型拉东傅里叶变换(improved Radon Fourier transform, IRFT)[4]、变尺度拉东傅里叶变换(scaled Radon Fourier transform, SRFT)[5]等。该算法的思路是通过对目标参数的多维联合搜索完成对目标信号的抽取,将目标能量投影到目标参数域完成积累与参数估计。该算法积累增益高,但计算量巨大,实时性较差;第2类算法为基于自相关处理的长时间积累算法。其典型算法有乘积型变尺度周期吕氏分布(product scaled periodic Lv’s distribution, PSPLVD)[6]算法、子孔径联合相参积累(subaperture joint coherent integration, SJCI)[7]算法等。这类算法通过自相关处理降低目标相位的阶数从而完成积累,无需对参数搜索,因此计算复杂度较低,但在低信噪比场景下失效;第3种算法为基于keystone变换的长时间积累算法。其典型算法有keystone变换-广义去调频算法(keystone transform-generalized de-chirp process, KT-GDP)[8]、keystone变换-吕氏分布(keystone transform-Lv’s distribution, KT-LVD)算法[9]等。这类算法的实现比较简单,复杂度不高,但需要考虑多普勒欠采样问题。
受启发于前人的研究工作,本文提出了一种新颖的长时间积累算法。首先,使用keystone变换(keystone transform, KT)完成线性距离校正,将目标能量集中到同一个距离单元内。此时,信号可以被建模为一个三阶相位信号(cubic phase signal, CPS)[10-11]。然后,运用相参积累型修正三阶相位函数(coherently integrated modified cubic phase function, CIMCPF)与相参积累型修正高阶模糊函数(coherently integrated modified high-order ambiguous function, CIMHAF)算法分别估计目标的一阶加速度与二阶加速度分量。最后,使用de-chirp技术将目标能量聚焦到距离-多普勒域完成积累。与现有同类算法相比,该算法具有三大优势。首先,该算法在CIMCPF与CIMHAF中利用信号的相参性完成了回波信号的二维积累,在低信噪比下目标检测能力优异;其次,由于该算法无需对多个目标参数做多维度联合搜索,仅需要快速傅里叶变换(fast Fourier transform, FFT)与非均匀离散傅里叶变换(nonuniform discrete Fourier transform, NUDFT)即可完成,因此计算复杂度较低;最后,该算法在多目标场景下对交叉项与伪峰的抑制能力较为显著。
文章的剩余内容由以下几部分组成。在第1节中,讨论信号形式与运动目标建模。第2节中展示了详细的算法流程。仿真实验、计算复杂度分析与噪声容限分析对比在第3节中给出。最后,第4节作了简要的总结。
1 问题描述
假设雷达发射线性调频信号为
s(tm,τ)=rect(τ/Tp)exp(jπμτ2)·exp[j2πfc(tm+τ)]
(1)
式中:rect(·)表示矩形窗函数;Tp表示脉冲持续时间;fc表示载波频率;τ表示快时间,也就是距离时间;Tr表示脉冲重复周期;μ表示调频率;tm=mTr(m=0,1,…,N-1)表示慢时间;N表示一个相参处理间隔内的所需处理的回波脉冲个数。
考虑到目标具有的高机动性,建立目标的运动模型方程可以如下表示:
(2)
式中:r0为目标与雷达间的初始距离;a1为速度,a2为一阶加速度,a3为二阶加速度。
雷达接收到的基带回波信号可以如下表示:
(3)
式中:A0为基带回波信号幅度;c为光速。
接着,对式(3)做下变频和脉冲压缩:
(4)
式中:A1为幅度值;λ=c/fc为雷达波长;B为回波信号带宽。
考虑到目标高速从而引起的多普勒模糊,将速度重新写为
a1=nkva+v0
(5)
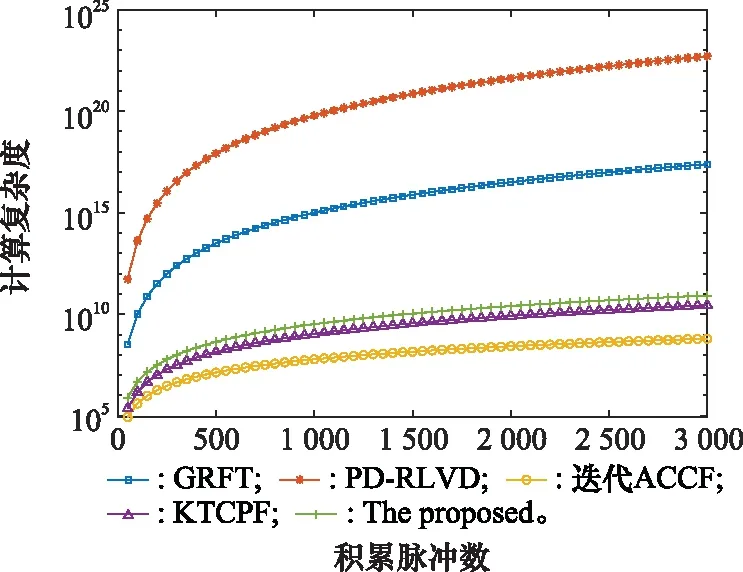
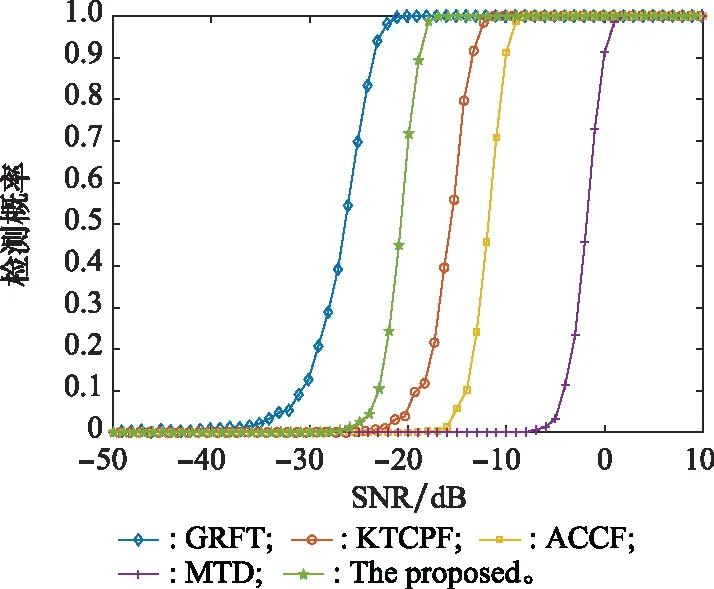
式中:nk为目标的模糊数(也被称为折叠因子);va=λfp/2为目标的盲速;v0=mod(a1,va)并且满足|v0| 将式(2)和式(5)代入式(4),可得 (6) 由式(6)可以看出,目标的包络位置会随着慢时间发生偏移,这将导致目标能量无法聚集在一个距离单元内;而指数相位项由于高阶分量的存在将导致多普勒扩散。 首先,对式(6)沿着快时间做FFT,可得 (7) 式中:A2为信号复幅度;f为快时间频率。 将式(2)结合式(5)代入式(7),可得 (8) 式中:幅度值A3=A2rect(f/B)。 接着,对式(8)做KT校正无模糊速度v0引起的距离走动。KT的定义如下所示: (9) 式中:tn为信号做完KT后的慢时间序列。 将KT的定义式代入式(8),并结合等式exp(-j2πfpnktm)=1,可得 (10) 在窄带条件下,有f≪fc,根据泰勒展开有fc/(f+fc)≈1与f/(f+fc)≈f/fc,因此式(10)又可以近似为 (11) 由式(11)可看出,目标的无模糊速度引起的距离走动已经消除。但盲速所导致的线形距离徙动依然存在,这将影响后续的能量积累。为此,构建补偿函数对其模糊数进行搜索: (12) 将式(12)与式(11)相乘: (13) 对式(13)沿着快时间做快速傅里叶逆变换(inverse fast Fourier transform, IFFT): (14) 当折叠因子n′与目标的真实折叠因子nk相等时,即n′=nk,可得 (15) 如式(15)所示,目标径向速度引起的线性距离走动已经被完全消除。目标能量集中在同一个距离单元内。可以建立如下搜索数据空间,以搜索折叠因子n′的估计值: (16) 当E(n′)达到峰值时,确定其位置即可完成搜索,得到模糊数的估计值,即 (17) 在完成距离校正后,目标能量被集中在了一个距离单元内,信号可以表示为如下形式: (18) 式中:A5表示信号幅度值。 首先对式(18)做修正瞬时自相关函数: (19) 式中:*为取复共轭操作;tk为延迟时间变量。 从上式可以看出,V0和a3的影响已经被消除,只剩下与a2有关的二阶项。沿着延迟时间tk做NUDFT,可得 (20) δ(tn-t0)g(tn)=g(t0)δ(tn-t0) (21) 式中:g(tn)是一个与慢时间tn相关的抽象函数,其形式可以不一,而t0是一个恒定慢时间常量。 利用以上性质,我们将式(20)乘一个特定的补偿函数进行重采样: (22) 式中: 接着,沿着慢时间tn做FFT可得 (23) (24) 为了便于分析,假设在理想情况下,一阶加速度的影响可以被完全消除。将式(24)与式(18)相乘,可得 (25) 接下来,我们需要估计目标的二阶加速度a3的值。根据高阶模糊函数的定义,我们对上式做如下变换: (26) 式中:tk为延迟时间变量。 由上式可以看出,慢时间tn与延迟时间tk存在耦合关系,且延迟时间为二阶。因此,我们不能直接用FFT积累,我们可以用如下方法解耦: (27) 从上式可以看出,MHAF信号能量在慢时间频率-延迟时间域沿着直线ftn=a3/λ分布。沿着延迟时间tk做FFT可得 (28) (29) 将式(29)与式(15)相乘可得 (30) (31) 最后,对假设满足式(31)要求的式(30)沿着慢时间做FFT,可得 (32) 因此,观察式(32)可得,通过慢时间FFT将回波信号重构成了近似sinc状点扩散函数。目标的回波能量在距离-多普勒域被有效地积累成一个尖峰,其中峰值位于(2r0/c,-2v0/λ)处。当峰值幅度与噪声幅度之比大于给定的阈值,则完成目标检测。 本文算法的流程框图如图1所示。 图1 所提算法流程框图 本小节通过Matlab数值仿真对本文所提出算法进行验证实验与对比分析。其中,本文所有实验所采用的雷达系统参数如表1所示。 表1 雷达系统参数 图2 单目标仿真结果 表2 单目标运动参数 其次,仿真验证了该算法在多目标场景下对交叉项的抑制能力。目标的运动参数如表3所示。雷达系统参数与单目标仿真实验完全一致。图3(a)为三目标回波的脉压结果,3个目标的脉冲能量均无法集中于各自的初始距离单元内。图3(b)为对信号做MCPF后的能量分布结果,目标能量在延迟时间频率维度沿着两条直线分布,能量杂散仍较为严重。完成相参积累后的CIMCPF信号能量聚焦结果如图3(c)所示。不难看出,经过相参积累后的二维频率域有两个明显的尖峰(目标B和C的一阶加速度相同,暂时无法分辨),且交叉项得到了有效地抑制。根据CIMCPF对3个目标的一阶加速度估计结果,完成de-chirp后目标A的CIMHAF积累结果如图3(d)所示,而因为目标C的一阶加速度和目标A不同,无法获得正确补偿,能量发生散焦,无法被检测。对目标B和C做MHAF后的能量分布如图3(e)所示。从图3中可以看出,由于二阶加速度不同,存在两条直线沿着延迟时间维分布,且能量杂散依然比较严重。图3(f)为目标B和目标C的CIMHAF积累结果,信号能量聚焦为两个明显的尖峰,且交叉项得到了有效地抑制,不会对后续的相参积累与参数估计产生虚警。通过以上仿真,证明了该算法在多目标场景下的有效性与对交叉项的强抑制能力。需要指出的是,当多目标的折叠因子不同或者目标的雷达散射截面积存在较大差异时,无法对所有目标同时进行处理,需要使用Clean技术分别对其进行补偿与积累,具体步骤参考文献[12]。 表3 多目标运动参数 图3 多目标仿真结果 假设Nr=Nt=N1=N2=Nv=NF=Nτ,5种算法的计算复杂度与脉冲采样点数的关系曲线如图4所示。从图4中可以明显地看出,本文所提算法的计算量远低于多维联合搜索算法,这将有利于目标检测与成像的实时处理;同时在没有显著提高计算量的前提下,相较于KTCPF与迭代ACCF算法有效提升了积累增益(这将在下面的仿真中证明)。 图4 脉冲点数与计算复杂度曲线 其次,仿真了不同信噪比(signal to noise ratio, SNR)下在利用KT完成距离校正的前提下,本文算法与经典的参数估计算法如极大似然估计(maximum likelihood, ML)[16]、广义霍夫高阶模糊函数(generalized Hough high-order ambiguity function, GHHAF)[17]、变尺度广义高阶模糊函数(scaled generalized high-order ambiguity function, SGHAF)[18]、乘积高阶相位匹配变换(product high-order matched-phase transform, PHMT)[19]、高阶模糊函数(high-order ambiguity function, HAF)[20]的均方根误差(root mean square error, RMSE)性能曲线。图5(a)与图5(b)中的统计结果分析表明,采用多维搜索获取参数估计值的ML算法的参数估计性能最佳,理论上接近于克拉美罗下界(Cramer-Rao lower bound, CRLB);而PHMT由于采用了六阶非线性变换,参数估计性能最差;HAF采用四阶非线性变换,但仅使用一维慢时间积累而没有利用延迟时间变量的自由度,因此低SNR环境下性能迅速恶化;另外,GHHAF由于采用霍夫变换估计二阶加速度,属于非相参积累,因此性能不佳;而SGHAF与本文算法均在二维时间域内实现了相参积累,在低SNR下接近于CRLB。 图5 参数估计性能分析 最后,仿真并对比了GRFT、KTCPF、循环迭代ACCF、MTD与本文所提算法的输入SNR与目标检测概率曲线。将检测目标的恒虚警概率设置为Pfa=10-6。对于每一SNR,都做500次蒙特卡罗实验。仿真对比曲线如图6所示。不难看出,GRFT通过多维度网格搜索的方式获得目标参数,可在高斯白噪声背景下近似为最优滤波器,因此检测性能最佳,而MTD算法由于无法校正距离走动与多普勒走动,检测性能最差。ACCF算法由于多次非线性处理导致积累增益损失很大,KTCPF算法由于没有在二维时间域采用相参积累,因此检测阈值比本文所提算法低4 dB左右。本文所提算法的检测阈值约为-23 dB,相较于全搜索算法,性能损失主要在于式(8)的KT插值运算、式(19)与式(26)的两次带噪信号互相关处理,由于两次均采用了四阶非线性变换,因此积累增益有所损失;另一方面,由于目标的一阶与二阶加速度无法同时完成估计,会存在传递误差,这也将导致参数估计要求的SNR比理论处理增益更高。 图6 SNR与检测概率曲线 为了解决高速高机动目标长时间积累中距离走动与多普勒走动效应,本文提出了一种基于KT、CIMCPF与CIMHAF的长时间积累算法。该算法首先使用KT校正了距离走动,再分别用CIMCPF与CIMHAF完成了高阶项参数的估计,最后在高阶相位补偿后完成回波能量在距离-多普勒域的聚焦。与现有同类算法相比,该算法无需多维搜索且能充分利用信号的相参性在二维时间域实现相参积累,并且解决了同一距离单元内多分量CPS的参数识别问题,因此具有计算复杂度低、交叉项抑制能力强与抗噪声性能优异等优点,具有广阔的应用前景,对雷达目标探测与参数估计有重要意义。
2 算法描述
2.1 KT距离校正
2.2 CIMCPF参数估计



2.3 CIMHAF参数估计

2.4 FFT完成积累


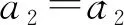


3 仿真实验与分析
3.1 仿真参数设置

3.2 算法仿真验证





3.3 与现有算法的对比



4 结 论

