基于集成深度学习的有源干扰智能分类

吕勤哲, 全英汇,*, 沙明辉, 董淑仙, 邢孟道

(1. 西安电子科技大学电子工程学院, 陕西 西安 710071; 2. 北京无线电测量研究所, 北京 100854;3. 西安电子科技大学前沿交叉研究院, 陕西 西安 710071)

0 引 言

雷达能够全天候实时获取远距离目标信息,以实现战场区域目标检测、跟踪或成像,在现代战争中占据重要地位[1-2]。随着数字射频存储器(digital radio frequency memory, DRFM)的发展,针对雷达的干扰措施不断加强[3],新型有源干扰技术能够实现多维、多域联合干扰,产生压制性、欺骗性的干扰效果[4],对雷达的战场生存带来严峻挑战[5]。现有的雷达抗干扰手段大多针对特定干扰类型,因此首先需要对雷达有源干扰进行准确分类识别,才能选择合适的抗干扰策略进行对抗[6],故研究雷达有源干扰的分类识别方法具有重要意义。

现有经典的雷达有源干扰识别研究主要包括两方面:基于似然准则的识别算法和基于专家特征提取与分类器设计的识别算法[7]。文献[8]针对多类噪声干扰机(noise-like jammer, NLJ)的识别问题,采用似然比测试和循环优化程序等方法,实现对未知数量NLJ的联合检测;文献[9]采用基于广义似然比检验的方法,研究了基于DRFM的欺骗干扰与目标分类识别问题。然而,基于似然准则的算法需要复杂的先验知识,并且计算复杂度高、应用场景受限。文献[10]通过平滑伪Wigner-Ville分布(smoothed pseudo-Wigner-Ville distribution, SPWD)对雷达回波信号进行时频分析,并计算其Zernike矩以构成人工特征向量,最终采用V-支持向量分类器(v-support vector classification, v-SVC)实现对多种拖引式欺骗干扰的分类。文献[11]通过对干扰信号变分模态分解,并计算矩形积分双谱及Renyi熵以组成特征参量,采用随机决策树与随机森林相结合的分类器实现多种有源干扰的分类。文献[12]结合双谱分析和奇异谱分析提取回波和干扰信号的特征参数,利用基于遗传算法的反向传播(genetic alogorithm back propagation, GA-BP)网络实现分类识别。然而,上述方法中人工特征提取需要先验知识且均存在计算量较大的问题。

近年来,深度学习逐渐被应用于雷达干扰识别领域,具有无需人工特征提取、鲁棒性强等优势[4,13-15],但基于深度学习的识别算法需要大量的训练样本,这在复杂战场电磁环境下非常困难;针对这一难点,本文提出一种基于多通道特征融合的集成卷积神经网络(ensemble convolutional neural network, ECNN)分类方法,该方法利用短时傅里叶变换(short-time Fourier transform, STFT)获取雷达回波信号的时频分布图,并提取其三通道特征以构建包含不同特征组合的增强化、多样化样本集,最终构建ECNN模型,充分融合并提取各样本集中多通道特征,实现小样本情况下多类有源干扰的智能化准确分类。

1 信号模型与STFT

本节将对线性调频(linear frequency modulation, LFM)信号以及7种单一雷达有源干扰的数学模型和产生机理进行简要分析,并对所采用的时频分析方法——STFT进行介绍,为后续有源干扰识别研究提供基础。

1.1 LFM信号

LFM信号是现代雷达常用的信号之一,具有大的时宽-带宽积,能同时获得较远的作用距离和较高的距离分辨率,因此本文采用LFM信号作为雷达发射波形,其时域信号[16]表达式为

(1)

式中：A为信号幅度；f0为信号中心频率;T为信号时宽;设B为信号带宽;则调频斜率k=B/T;rect(t/T)为矩形函数,定义为

(2)

LFM信号对宽脉冲进行调制,使得频率连续线性变化,增加了信号的发射带宽,并通过脉冲压缩实现宽脉冲下高距离分辨率。

1.2 雷达有源干扰模型

雷达有源干扰可分为有源压制式干扰和有源欺骗式干扰,选取典型干扰样式建立数学模型并进行实验,其中有源压制式干扰[17-18]包括瞄准式干扰(spot jamming, SJ)、阻塞式干扰(blocking jamming, BJ)、线性扫频式干扰(linear sweep jamming, LSJ)[19];有源欺骗式干扰包括距离欺骗干扰(range deception jamming, RDJ)[20]、密集假目标干扰(dense false target jamming, DFTJ)[21]、间歇采样转发干扰(interrupted-sampling repeater jamming,ISRJ)[22]、灵巧噪声干扰(smart noise jamming, SNJ)[23]。

1.2.1 有源压制干扰

根据有源压制干扰对雷达接收机的作用类型,压制性干扰可分为SJ、BJ和LSJ[24]。

(1) SJ

SJ通常满足以下条件:

(3)

(2) BJ

BJ的带宽通常满足Δfj≥5Δfr,其干扰带宽大且对频率导引要求较低,能够全覆盖式干扰雷达的工作频段,但其干扰功率密度较低,造成在雷达工作频带外的功率浪费。

(3) LSJ

本文所采用的LSJ[25]满足以下条件:

(4)

由式(4)可知,与SJ不同的是,其干扰中心频率fj为周期函数,通过设置较宽的扫频范围,能够对雷达造成周期性的压制效果。

1.2.2 有源欺骗干扰

(1) DFTJ

DFTJ通过对干扰机截获雷达信号进行多次延迟、叠加转发,能够在形成多个不同距离假目标的同时消耗雷达资源,其时域模型可表示为

(5)

式中：M为假目标转发次数；Am为第m次转发的干扰调制幅度;t0和τm分别为真实目标时延和第m次干扰转发时延。

(2) RDJ

RDJ通过对所截获雷达信号进行调制并延迟转发,为保证逼真的欺骗干扰效果,通常只进行幅度调制,其时域表达式为

J(t)=AJS(t-t0-τ0)

(6)

式中:AJ为干扰幅值;t0和τ0分别为真实目标时延和干扰转发时延。

(3) ISRJ

ISRJ通过干扰机“收发分时”体制,对所截获雷达信号进行多次转发,以实现干扰目的[26],其时域模型可以表示为

(7)

式中：N为切片数目;切片宽度为TW;M为单个切片转发次数。

(4) SNJ

SNJ通过对干扰机所截获的雷达信号进行噪声调制,从而同时具有噪声干扰和欺骗干扰的效果。本文选取调幅灵巧噪声干扰,采用高斯白噪声与间歇采样转发干扰相乘,其时域表达式如下:

J(t)=n(t)·JISRJ(t)

(8)

式中:n(t)是均值为0,方差为σ2的高斯白噪声。

1.3 STFT

STFT又称作加窗傅里叶变换,其基本思想是设计一个时域窗函数φ(t)与待分析时间信号x(t)相乘,将其分割为多个时间段信号,然后对每个时间段信号做傅里叶变换,最终得到完整时间信号的时频分布情况,STFT数学表达式[26-27]如下:

(9)

式中:τ为窗函数中心位置。由式(9)可知,STFT是线性变换的,因此在时频分析中不会产生交叉干扰项。研究表明,若滑窗时间越短,时频分析的频率分辨率越低、时间分辨率越高;若滑窗时间延长,则其时间分辨率降低、频率分辨率升高,即STFT无法同时满足时域、频域的高分辨率需求[28]。

2 雷达有源干扰智能分类

本文所提基于集成深度模型的有源干扰智能分类流程如图1所示,主要利用STFT获取干扰样本的时频分布数据,并通过多通道特征组合方法得到不同时频特征组合的样本集,以实现特征多样化融合并增强数据多样性,采用集成深度模型实现对各样本集的自动特征提取、类别预测及决策融合,最终实现对多型有源干扰的智能化分类识别。

图1 基于集成深度模型的有源干扰智能分类流程

2.1 集成深度模型

集成学习是一种元算法,能够调用机器学习算法构成基分类器并采用随机子空间技术[29]、决策融合等方式将若干基分类器组合成一个集成学习模型,以提高模型泛化性能。深度学习算法具有强大的非线性特征提取能力,本文所设计的集成深度模型采用卷积神经网络(convolutional neural network, CNN)作为基分类器,利用其强大的特征提取、分类能力对输入样本集进行独立分类,并采用多数投票方法对各基分类器的预测标签进行决策融合,最终得到集成深度模型的预测结果。本文所设计的CNN模型包括卷积层、池化层、正则化层和全连接层等,分别介绍如下。

(1) 卷积层

卷积层使用卷积运算替代普通全连接层的相乘运算,是CNN与传统神经网络的最大区别之处。设输入为融合多通道特征的三维矩阵X,其大小为m×n×d,其中m×n为时频谱图大小,d为样本所含特征通道数,设第一个卷积层具有k个滤波器,则第j个滤波器的输出[30]可表示为

(10)

式中:xi是X的第i个特征矩阵;*代表卷积运算;wj和bj分别代表第j个滤波器的权重和偏置量;f(·)是激活函数,用于增强模型的非线性表示能力,本文采用ReLU激活函数,表示为

f(x)=max(0,x)

(11)

(2) 池化层

池化层对输入特征矩阵进行降采样操作,即首先将输入特征矩阵分割为多个子块(可重叠),然后对每个子块取平均值(平均池化)或最大值(最大池化)作为该子块的特征表示。

(3) 正则化层

正则化层通过降低模型的存储信息量来优化模型,使其学习最重要的模式以减少过拟合风险,并提高模型泛化性能。本文在CNN模型中添加dropout正则化层以提高小样本情况下算法的泛化性能,其主要思想是在模型训练过程中随机地将该层β%的输出特征置0;由于测试过程中不置0,故将该层输出值按β%缩小以保持平衡。

(4) 全连接层

在CNN模型中,全连接层通常起到分类器的作用,即将模型所提取的分布式特征映射到各个样本标签。本文所设计CNN模型中的全连接层采用Softmax激活函数,计算分类器输入z属于第c类的概率,其数学表达式为

(12)

式中:C为类别总数;θ为分类器参数。

2.2 基于多通道特征融合的ECNN算法

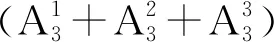
步骤 1按照第1节中雷达发射波形与干扰信号模型仿真建立雷达回波信号时域数据集,其中共包含N个时域序列样本;

步骤 2对时域数据集中N个样本分别采用STFT并提取其实部、虚部和模值特征以得到大小为N×(m×n×3)的时频分布数据集;

步骤 3在时频分布数据集中提取实部、虚部和模值三通道特征,进行15种特征组合并分别构建大小为N×(m×n×nf)的样本集Se,依次选取每类样本的α%作为训练样本集,其余1-α%为测试集;

步骤 4设计基分类器CNN并构建包含15个独立基分类器的ECNN模型,利用ECNN模型的各个基分类器分别对15个样本集进行特征提取和分类,采用多数投票方法获得集成模型的整体预测结果。

3 仿真实验及分析

为了验证本文所提基于多通道特征融合的ECNN算法的有效性,仿真多种单一及复合干扰信号数据进行实验分析。雷达发射波形采用LFM信号,设置信号时宽T=20 μs,带宽B=10 MHz,采样率fs=20 MHz,真实目标信噪比(signal-to-noise ratio, SNR)为0 dB;每个时域样本即距离门长度为2 000点,且真实目标随机出现在每个距离门中任意位置,仿真产生仅含真实目标的回波信号以及第1.2节中所介绍的7种单一有源干扰信号,其参数如表1所示。为提升干扰场景的复杂性,仿真产生RDJ+SNJ、DFTJ+SNJ、RDJ+ISRJ以及LSJ+ISRJ共4种复合干扰类型,上述12类信号每类仿真500个样本,即样本总数为6 000,每类样本时域波形如图2所示;对每个时域样本采用STFT以生成时频分布样本集,其中输入时域样本被分为32段,各段间重叠采样点数为8点,窗函数选用Hamming窗,傅里叶变换点数NFFT=100,故所得每个时频分布样本大小为247×100,其时频谱图如图3所示;最后提取三通道特征以构建大小为6 000×(247×100×3)的时频分布样本集S,并采用特征组合方法分别构建15种样本集Se。分别选取每类样本的8%、6%、4%和2%作为训练样本,其余全部作为测试样本,从而构建各类样本数目平衡的样本集。

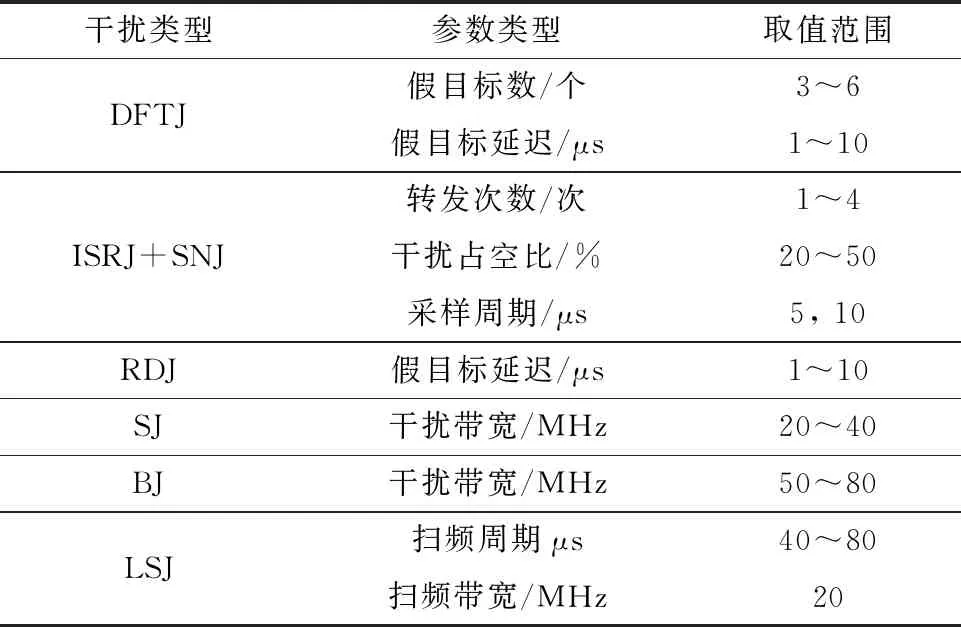
表1 干扰信号仿真参数

图2 干扰信号仿真数据时域波形图

图3 干扰信号仿真数据时频谱图

本文所设计的ECNN模型包含15个基分类器CNN,每个CNN的详细结构参数如表2所示,主要包含4个卷积层、池化层和2个正则化层。为验证本文所提算法的有效性和优越性,分别利用表2、表3所示CNN模型在时频域、时域三通道干扰数据集上进行对比分类实验,并采用文献[7]所提出的有源干扰信号分类算法作为对比,即提取了干扰信号均值、方差、频域矩偏度、频域矩峰度、盒维数、近似熵以及分数低阶矩等7维人工特征,采用随机森林(random forest, RF)分类器进行干扰信号分类,其中RF所包含决策树数目为100。为明确地衡量各个算法的泛化能力,采用整体精度(overall accuracy, OA)、平均精度(average accuracy, AA)作为分类性能评价指标,所有实验结果均为10次独立重复实验取平均,以提高实验结果的可靠性。

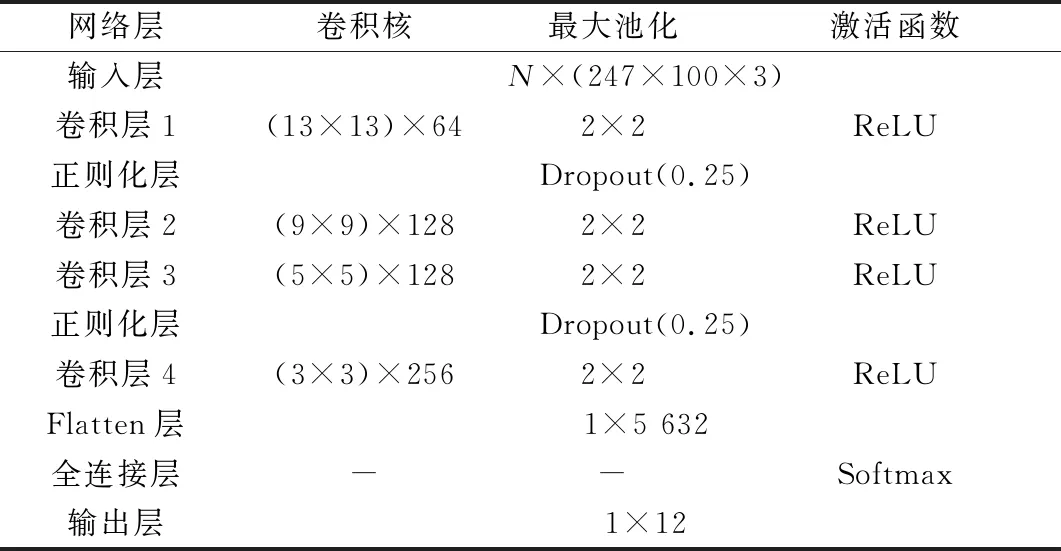
表2 基础分类器CNN模型参数

表3 时域CNN模型参数

上述4种算法的实验结果分别如图4所示,在训练样本数占8%(较为充足)的情况下,4种算法均取得了较好的实验结果,当训练集大小依次减少到2%时,各个算法的精度都依次下降。利用本文所生成时频域数据集进行分类的时频域三通道CNN算法及ECNN算法的精度均高于时域三通道CNN算法精度与基于特征提取的RF算法的精度,且所提ECNN算法精度始终为最佳,即具有最佳泛化能力;在不同训练样本的实验中,其OA相比传统基于人工特征提取的RF算法提高3.87%～7.93%,相比时域三通道CNN算法提高0.97%～16.70%,相比时频域三通道CNN算法提高1.55%～4.54%;其AA相比传统基于人工特征提取的RF算法提高2.81%～6.95%,相比时域三通道CNN算法提高0.82%～16.52%,相比时频域三通道CNN算法提高1.39%～4.27%;由此可见,所提ECNN分类算法在2%的训练样本下较之对比算法的精度提升最多,模型泛化能力更好。

图4 雷达干扰智能分类结果

表4详细给出了训练样本占4%时4种算法实验结果的每类精度,其中每类干扰的最佳分类精度用加粗字体显示,本文所设计的ECNN算法在9种干扰类别中取得了最佳分类效果,且该算法重复实验所得分类结果的方差最小(稳定性最高),较之对比算法有着显著优势。

表4 训练集占4%时的每类精度

续表4

4 结束语

为了解决传统雷达有源干扰分类算法需要构建人工特征集,且小样本情况下分类精度较低的问题,本文提出一种基于多通道特征融合的ECNN分类算法;通过结合集成学习与深度学习的优势,实现对雷达干扰数据实部、虚部和模值特征的充分融合与特征提取,最终实现对雷达有源干扰的智能化准确分类,相比传统基于特征提取的RF算法与时域三通道CNN以及时频域三通道CNN算法的分类精度更高、算法稳定性更好。

本文所提ECNN算法仍存在深度学习模型耗时较长且仅采用了仿真数据进行实验等问题,引入实测数据进行实验并优化算法以减少模型训练时间是下一步研究工作的重点。