基于线性约束最小方差原则的稳健快速自适应脉冲压缩方法

裴家正, 黄 勇,*, 陈宝欣, 关 键, 陈小龙

(1. 海军航空大学航空作战勤务学院, 山东 烟台 264000; 2. 中国人民解放军92337部队, 辽宁 大连 116000)

0 引 言

基于大时宽-带宽积信号的脉冲压缩技术可以同时保证雷达系统对较远雷达探测距离和较高距离分辨率的要求。作为脉冲压缩技术的常用方法,匹配滤波(matched filter, MF)是在点目标和高斯白噪声条件下,以最大化输出信噪比为准则的最优线性滤波器[1-3]。

然而实际应用中,MF的输出存在强目标距离旁瓣遮蔽其他弱目标等问题。为了更好地抑制旁瓣,多种失配滤波方法[4-8]在一定程度上实现了抑制效果。此外，较有代表性的便是基于迭代最小均方误差(iterative minimum mean square error, RMMSE)准则的自适应脉冲压缩(adaptive pulse compression, APC)方法[9],该方法迭代地利用邻近距离单元的功率值为每个距离单元设置自适应滤波器,构造自适应零陷压低旁瓣。随后Blunt不仅将APC方法推广至共享频带的多基地雷达中[10]，又研究了自适应脉冲压缩修复(pulse compression repair, PCR)方法[11]将MF的输出结果作为发射波形进行APC,对多普勒失配和系统误差具有更强的稳健性;还提出了先进行多普勒补偿,再进行APC抑制运动目标的距离旁瓣[12-13]。为进一步降低APC方法较高的计算量,Blunt等结合降维算法提出了快速APC (fast APC, FAPC)方法,主要包括抽取分块FAPC(decimation FAPC, DFAPC)方法和连续分块FAPC(contiguous block FAPC, CFAPC)方法[14-15]。FAPC方法在减少计算量的同时保持了APC的大部分性能增益,但降低了算法的自由度,会在较密集的散射环境中抑制小目标。因此Higgins等后续提出了基于最小方差无畸变响应(minimum variance distortionless response, MVDR)原则的CFAPC(MVDR-CFAPC)方法[16],将增益保留在小目标上,从而提高了检测性能。

在APC方法基础上,近年来的研究不仅有借鉴空域阵列的处理方法提高了APC方法抑制干扰、杂波的能力[17];也有借鉴线性贝叶斯理论、并行运算等降低APC方法的计算量[18-19];还有探索多输入输出雷达体制下的APC方法[20-21],这些改进不但解决了相应的问题,还依然具备较好的旁瓣抑制效果。但以上研究大部分在讨论APC方法性能时都默认距离单元内回波采样点位于目标点上。对于常见的连续时间相位调制波形,如线性调频(linear frequency modulation, LFM)信号波形等,由于目标点随机分布于距离单元内,因此在回波采样的过程中极有可能回波采样点没有位于目标点上,造成二者失配的情况(也可称为采样失配)。在APC处理中,如果出现采样失配,基于回波数据的APC滤波器将难以形成深凹口,其性能损失十分明显。为此,Henke等将基于最小二乘的失配滤波方法和APC方法应用于调频波形,提出对回波过采样抑制采样失配所引起的距离旁瓣[22],但是对回波过采样所带来的计算量十分显著。李秀友等通过设置主瓣宽度和干扰零点约束条件,提出了一种基于线性约束最小方差(linearly constrained minimum variance, LCMV)准则的APC方法[23],以解决采样失配和强目标距离旁瓣遮蔽弱目标的问题,然而该方法需要估计强弱目标的相对强度和位置,实际中难以划分合适的强弱目标相对值。

本文在MVDR-CFAPC方法的基础之上进行改进。MVDR-CFAPC方法在LFM信号波形采样失配时具备一定的稳健性，但是其稳健性并不稳定。为此,本文借鉴导向矢量失配情况下基于线性约束最小方差原则的稳健自适应波束形成算法,在不对回波过采样的前提下提出将基于LCMV原则的CFAPC方法应用于LFM信号的脉冲压缩处理中,在LFM信号回波采样匹配和失配情况下都具备较为稳定的距离旁瓣抑制性能。本文最终通过仿真和实测数据实验验证了该方法的稳健性。

1 采样失配问题的相关分析

假设场景中共有L个距离单元,在每个距离单元中有Nsample个采样点,每个距离单元取一个采样点。采样的发射信号波形可以通过准确抽取每个距离单元内的第1个采样点取得,发射信号波形的N维采样点组成的矢量可以表示为s=[s(0),s(1),…,s(N-1)]T。采样的回波信号波形也是在每个距离单元中Nsample个采样点里抽取其中的一个,如果回波信号波形的采样点位于目标点上,则视为采样匹配。采样匹配时距离单元l(l=0,1,…,L-1)处的雷达回波信号y(l)为

y(l)=xT(l)s+v(l)

(1)

式中:x(l)=[x(l),x(l-1),…,x(l-N+1)]T表示场景真实距离维响应的N点连续采样;v(l)为距离单元l处的加性高斯白噪声。MF的脉压输出表示为

xMF(l)=sHy(l)=sHAT(l)s+sHv(l)

(2)

式中:y(l)=[y(l),y(l+1), …,y(l+N-1)]T为回波的N点连续采样且y(l)=AT(l)s+v(l);A(l)=[x(l),x(l+1),…,x(l+N-1)];v(l)=[v(l),v(l+1),…,v(l+N-1)]T为噪声矢量;(·)H为共轭转置运算。

MVDR-APC方法通过构造代价函数J(l)=E[|x(l)-wH(l)y(l)|2]推导最优滤波器系数,E(·)表示期望[9,24]。在单位增益无畸变约束wH(l)s=1下,利用拉格朗日乘数法最小化代价函数[25]可得

(3)

式中:Ry(l)=Rx(l)+R(l)为回波协方差矩阵,R(l)=E[v(l)vH(l)]为噪声协方差矩阵,Rx(l)为信号协方差矩阵:

(4)

其中,ρ(l+n)=|x(l+n)|2为距离单元(l+n)处的功率值;sn为以s为基础进行移位的N维矢量:

(5)

由于无法准确确定目标点在距离单元内的分布,如果采样的LFM信号回波波形在Nsample个采样点中抽取的采样点不是目标点,那么二者之间就是失配的。令回波采样点与目标点之间的失配时间为Δt(-0.5Ts<Δt≤0.5Ts,Ts为回波采样间隔),如图1(a)所示，回波采样点超前目标点时Δt为负；如图1(b)所示,回波采样点落后目标点时Δt为正。

图1 采样失配时间Δt示意图

以平静海面上一艘海盗游艇隐藏在货轮周围企图掩盖行踪的情况为例,仿真场景中设置一强一弱两目标A和B,信噪比分别为60 dB和15 dB。图2为仿真回波采样点和强目标点之间采样匹配和失配0.5Ts情况下(不存在脉内多普勒频率)的脉压输出。在采样匹配情况下MF(包括加Taylor窗的MF)脉压输出带有明显的距离旁瓣,而MVDR-APC方法抑制了距离旁瓣。但在采样失配0.5Ts情况下,MVDR-APC方法的脉压输出中强目标也产生了较大的距离旁瓣,遮蔽了弱目标,与采样匹配的情况相比,性能明显下降。

图2 采样匹配和采样失配0.5 Ts时MF,加Taylor窗MF, MVDR-APC的输出

2 LCMV-CFAPC

为了在LFM信号的APC处理中抑制因采样失配而引起的距离旁瓣,本节首先证实MVDR-CFAPC方法对LFM信号波形采样失配具备一定的稳健性;而后改进MVDR-CFAPC方法,得到更稳健的LCMV-CFAPC方法。

2.1 针对LFM信号脉压的MVDR-CFAPC方法

CFAPC方法将APC处理的N维信号模型连续分割成M块,并且每一块中的元素个数为K=N/M,得到的第m块(1≤m≤M)信号模型[14]为

(6)

图3 回波信号的连续分块示意图

MVDR-CFAPC方法的代价函数通过拉格朗日乘数法表示为

(7)

(8)

其中,

(9)

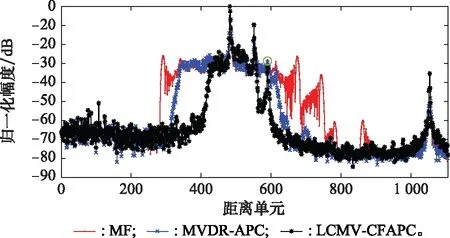
相比相位编码信号,LFM信号多普勒容忍性更强,但是对采样失配问题更敏感。在LFM信号回波采样失配时,MVDR-CFAPC方法相比MVDR-APC方法处理时间较短(因为K

图4为MVDR-CFAPC方法在图2场景中强目标点采样失配0.5Ts时M取不同值的脉压输出结果。当分块数M取接近于波形长度N的最大约数,即M=N/2时,在采样失配时间维放置的零点最多,相比M取其他值脉压主瓣宽度以及旁瓣抑制更优。

图4 采样失配0.5 Ts时MVDR-CFAPC方法中 M取不同值的输出

但当采样失配时间为其他值(为节省篇幅图5以采样失配0.2Ts和-0.25Ts情况为例),在强目标点左右各N/2处旁瓣有所抬升,可见MVDR-CFAPC方法在(-0.5Ts, 0.5Ts]的采样失配区间内的性能并不稳定,因而需要继续改进得到更稳健的输出。

图5 采样失配0.2 Ts和-0.25 Ts情况下的MVDR-CFAPC输出

2.2 针对LFM信号脉压的LCMV-CFAPC方法

为了保证APC方法在采样失配区间内都能保持更好的稳健性,本节借鉴导向矢量失配情况下的稳健自适应波束形成算法[26-31],在MVDR-CFAPC方法中的无畸变约束条件基础上施加更多的约束条件[32],得到LCMV-CFAPC方法,通过增加的约束抑制不希望存在的距离旁瓣以获得更稳定的脉压输出。

(1) 设置零点约束条件

(10)

由此,LCMV-CFAPC方法的全维代价函数为

(11)

(3) 利用拉格朗日乘数法,全维代价函数重新写为连续分块之和的形式:

(12)

(13)

式中:Cm是由约束条件矩阵C的第(m-1)K+1行到第mK行组成的第m个子阵,且

(14)

(15)

式中:sm,k是以sm(s的第(m-1)K+1个到第mK个元素组成的第m个分块矢量)为基础进行移位的K维矢量:

sm,k=[s((m-1)K-k),s((m-1)K-k+1),…,s(mK-k-1)]T

(16)

若在移位过程中,k<-N+mK或k>(m-1)K使得(m-1)·K-k,(m-1)K-k+1,…,mK-k-1中的一个或多个索引值为小于0或大于N-1时,需要将sm,k中对应位置的元素用0补齐。

(4) 设置分块协方差的置零条件

ρ(l+k+(m-1)K)=0, 0<|k+(m-1)K|

(17)

(18)

(6) 迭代运算

当连续分块数M取N/2时,LCMV-CFAPC方法的脉压主瓣宽度仍然为最优。按照(1)～(5)计算每个距离单元的最优权矢量,迭代5～6次便可通过LCMV-CFAPC方法实现较稳健的脉压输出。

3 实验分析

为了较全面地分析LCMV-CFAPC方法的性能,本节首先考虑各个方法分别在图2场景中采样匹配、脉内多普勒失配、采样失配0.5Ts、采样失配0.2Ts、采样失配-0.25Ts等仿真情况下的脉压性能。所有仿真场景下将强目标左右N-1个距离单元范围内计算平均峰值旁瓣电平(average peak sidelobe level, APSL)作为性能指标,作为估计值,需要多次仿真取平均,一次仿真的APSL计算为

(19)

式中:lmax为强目标所在距离单元;SNR(lmax)为强目标的信噪比;I为lmax左右N-1个距离单元集合,且不包含其他目标主瓣位置;SNR(i)为距离单元i处的信噪比。之后本节在多目标采样失配程度互异的仿真条件下比较各个方法的距离旁瓣抑制效果。最后借助实测数据实验,进一步对比分析方法性能。

3.1 仿真场景下的方法性能对比

仿真场景中一共有L=500个距离单元。LFM信号带宽B为5 MHz,时宽τ为10-5s,时宽-带宽积Bτ=50,N=50。令采样频率Fs等于带宽B即可使一个距离单元中有一个回波采样点,且采样间隔Ts=1/B。为了仿真模拟信号的数字采样过程,Fs为160 MHz,则Nsample=32,一个距离单元中有32个回波采样点。为了简化问题的表述,假设目标点位于距离单元中的第17个采样点。如果回波采样点是通过抽取每个距离单元中的第17个采样点取得,则为采样匹配情况;如果回波采样点不是第17个采样点,则为采样失配情况。

(1) 采样匹配情况下的性能仿真

按照图2的仿真场景,两目标A和B信噪比分别为15 dB和60 dB,位于第280个和第300个距离单元。在采样匹配情况下,目标无脉内多普勒频率时,各方法的脉压性能如图6所示。

图6 采样匹配时各方法的脉压性能

图6中MF输出存在强目标旁瓣遮蔽弱目标的现象,APSL为35.4 dB。全维度的MVDR-APC方法在采样匹配情况下的脉压效果最好。MVDR-APC,MVDR-CFAPC和LCMV-CFAPC方法在采样匹配时的脉压输出APSL分别为76.7 dB,74.5 dB,74.3 dB, 3种方法都可以抑制强目标旁瓣,还原出弱目标的主瓣。

(2) 脉内多普勒失配下的性能仿真

本组实验令目标A脉内多普勒800 Hz,目标B脉内多普勒1 000 Hz,对回波采样点与目标点采样匹配的情况继续进行分析。

在具有脉内多普勒频率时MVDR-APC方法的脉压输出强目标距离旁瓣存在但不明显,APSL为73.4 dB,相比于无脉内多普勒频移时下降3.3 dB。由于CFAPC方法对脉内多普勒频率的容忍性更强,MVDR-CFAPC和LCMV-CFAPC方法的脉压输出结果较好,APSL分别为74.2 dB和74 dB。

(3) 采样失配0.5Ts下的性能仿真

目标A和B的脉内多普勒频率与(2)相同,回波信号波形采样失配0.5Ts情况下各个方法的脉压性能如图8所示。

图7 脉内多普勒失配时各方法的脉压性能

图8 采样失配0.5 Ts时各方法的脉压性能

根据图8与图7的对比可得出,脉内多普勒失配与采样失配同时存在时,采样失配对APC方法的影响占据主导地位。此时MVDR-APC方法的脉压旁瓣已经完全遮蔽了附近的弱目标。MVDR-CFAPC和LCMV-CFAPC方法仍然可以在脉内多普勒频率与采样失配同时存在时达到较好的旁瓣抑制性能,但是二者的输出之间仍然存在较细微的差别。

(4) 采样失配0.2Ts下的性能仿真

目标A和B的脉内多普勒频率与(2)相同,回波信号波形采样失配0.2Ts情况下各个方法的脉压性能如图9所示。图9中最明显的是MVDR-CFAPC方法的脉压输出在强目标左右N/2处出现了新的距离旁瓣,其APSL为71.1 dB。而LCMV-CFAPC方法因为添加了抑制旁瓣干扰的约束,仍然可以达到较好的旁瓣抑制性能,其APSL为72.5 dB。

图9 采样失配0.2 Ts时各方法的脉压性能

(5) 采样失配-0.25Ts下的性能仿真

本组实验采样失配时间-0.25Ts,且目标A、B的脉内多普勒频率与(2)相同。图10中MVDR-CFAPC方法强目标左右N/2处距离旁瓣也存在。虽然APSL为65.7 dB,稍好于采样失配0.5Ts的情况,但LCMV-CFAPC方法能够在失配时间为-0.25Ts时保持更好的旁瓣抑制性能,APSL保持在68.3 dB。

图10 采样失配-0.25 Ts时各方法的脉压性能

为更直观地比较,以上不同实验组各个方法的APSL如表1中所示。综合比较而言，LCMV-CFAPC方法更具备稳健性。

表1 各个方法在仿真实验中脉压输出的APSL

考虑不同采样失配时间下不同方法的性能,根据以上仿真场景得出无脉内多普勒时以上4种方法的APSL仅随采样失配时间Δt变化的关系。从图11可以明显看出,MVDR-APC方法在采样匹配的情况下脉压效果极佳,可是一旦发生采样失配问题,其脉压的APSL急剧下降。由于MVDR-CFAPC方法与LCMV-CFAPC方法是降维版本,采样匹配情况下的APSL都稍低一些;但是在采样失配情况下APSL数值更大且相比MVDR-APC方法的变化更平缓,说明两种方法都更稳健。Δt在采样失配区间变化时,LCMV-CFAPC方法的APSL比MVDR-CFAPC方法的更大一些。另外，图9和图10中MVDR-CFAPC方法脉压输出旁瓣有所抬升,综合之下LCMV-CFAPC方法仍然更加稳定。

图11 APSL与采样失配时间Δt的关系图

3.2 多目标采样失配下的方法性能对比

本节实验在场景中随机设置12个目标,目标的信噪比和脉内多普勒频率分别在[15 dB, 60 dB]和[-1 000 Hz, 1 000 Hz]的区间内随机取值。在多目标每个目标点的采样失配时间在(-0.5Ts, 0.5Ts]区间之间随机取值的情况下各个方法的脉压输出性能对比如图12所示。图中经过脉压后可被明显发现的目标被红色圆形标出。

图12 采样失配与脉内多普勒同时发生时多目标不同方法的脉压性能

在目标较多时MVDR-APC方法的脉压性能退化依然严重,MVDR-CFAPC方法的脉压输出也存在强目标脉压旁瓣遮蔽部分弱目标的现象。为通过数值比较各种方法在多目标采样失配场景下的性能,本节计算每个目标的APSL取平均值作为量化比较的性能指标。在MF的输出中4个弱目标被强目标旁瓣遮蔽,目标APSL平均值为18.97 dB,进一步说明了MF的脉压具有较高旁瓣的问题。MVDR-APC方法的输出中4个弱目标同样被强目标旁瓣遮蔽,目标APSL平均值为25.99 dB。MVDR-CFAPC方法虽相比MVDR-APC方法较好,但其输出中仍然有两个弱目标被强目标旁瓣遮蔽,目标APSL平均值为35.47 dB。综合比较而言LCMV-CFAPC方法性能最优,其输出中各目标的主瓣都比较明显,目标APSL平均值为40.04 dB。可以看出,在整个仿真实验中,MVDR-CFAPC和LCMV-CFAPC方法对于脉内多普勒频率和采样失配同时存在时相较于MVDR-APC方法都更加稳健,但总的来说LCMV-CFAPC方法的稳健性更好。

3.3 实测数据下的方法性能对比

本节实验选取部分采自X波段雷达实测数据,分别利用MF,MVDR-APC,LCMV-CFAPC 3种方法对该实测数据进行脉冲压缩处理。此X波段雷达所发射信号波形的时宽带宽积为75,且实测数据中共存在4个目标,大致位于场景中的第480,第550,第590和第1 050个距离单元处。3种方法的脉压输出如图13所示,图中的绿色圆形标记出了经过MF方法和MVDR-APC方法脉压输出无法发现的目标。由图13可知,MF方法的脉压输出中强目标的脉压旁瓣直接遮蔽了绿色圆形标记的弱目标;MVDR-APC方法稍好一些,强目标的脉压旁瓣被有效地抑制,但仍然遮蔽了绿色圆形标记的弱目标;LCMV-CFAPC方法的脉压输出中可以较轻易地发现该弱目标,进一步证实LCMV-CFAPC方法的脉压输出更清晰,处理实测数据时该方法的脉压处理性能仍然更加优异。

图13 处理雷达实测数据时不同方法的脉压性能

3.4 算法复杂度分析

由于APC方法设计迭代运算,分析时只分析一次迭代运算中的计算成本。在时域中实现的MF相当于仅有一次迭代,而且其计算成本为每个距离单元进行N次乘积,对每个距离单元其计算成本为N[15]。常规的MVDR-APC方法可根据矩阵求逆定理进行秩一更新[9],快速计算每个单独的距离单元的N×N维协方差矩阵。针对每个距离单元,其计算成本为6N2+14N[15]。

MVDR-CFAPC方法对协方差矩阵分块,对应于第l个距离单元的信号协方差矩阵与第l-K个距离单元的协方差矩阵的子阵之间具有如图14所示的对应关系,因此前K个距离单元之后每个距离单元的协方差矩阵只需更新一个K×K维矩阵[15]。另外MVDR-CFAPC方法也可以进行快速矩阵更新,其计算成本为N2(3/M+3/M2)+N(1+13/M)[15]。

图14 CFAPC中与子阵的对应示意图

LCMV-CFAPC方法一方面增加了零点约束条件,另一方面是分块协方差的置零操作。二者的计算成本一共为N2/M+N2/M2+2N,使得LCMV-CFAPC方法的计算成本为N2(4/M+4/M2)+N(3+13/M)。算法中M=N/2,可见针对单个距离单元,LCMV-CFAPC方法一次迭代的计算成本明显低于MVDR-APC方法,仍属于快速APC方法。

为了进一步分析算法复杂度,表2～表4列举出第4.1～第4.3节中各个方法在MatlabR2019b和COREi7-9750H环境下多次运行得到的一次迭代平均耗时比较。

表2 第4.1节中各方法一次迭代的平均耗时

表3 第4.2节中各方法一次迭代的平均耗时

表4 第4.3节中各方法一次迭代的平均耗时

从表2和表3仿真实验耗时对比中看出,相比于MF,APC方法耗时确实较长。虽然MVDR-CFAPC和LCMV-CFAPC方法的平均耗时长于MVDR-APC方法,但是其迭代次数是MVDR-APC方法的两倍。如果按照一次迭代耗时来比较,LCMV-CFAPC方法耗时介于MVDR-CFAPC和MVDR-APC方法之间。

根据表4实测数据实验耗时对比仍然可以得到相同的结论,对于第4.3节实测数据处理,由于实验测试是通过有限的软硬件来实现的,表4中的结果可作为参考。耗时结果跟环境配置紧密相关,具体到实际运用中的耗时还是要结合具体算法,实验过程以及数字信号处理计算平台继续优化。

4 结 论

LFM信号在现代雷达信号处理中应用广泛。信号回波波形采样点与目标点之间采样失配对APC影响十分明显。本文在LFM信号脉冲压缩处理的应用场景下,借鉴导向矢量失配情况下的稳健自适应波束形成算法,以CFAPC为基础先增加了零点约束条件,又对分块协方差矩阵设置置零条件,从而提出了一种LCMV-CFAPC方法。仿真实验和实测数据一致表明,该方法不需要对回波过采样,不仅在采样匹配情况下保持正常的脉压性能,还可以在采样失配情况下保持优于常规APC方法的稳健性,相比于常规MVDR-CFAPC方法,本文所提方法的性能也更加稳定。不过目前FAPC的耗时相比于传统方法仍然较长,后期研究将着重于探索匹配滤波与FAPC相结合,进一步提高算法效率。