基于麻雀搜索算法结合深度前馈神经网络的近红外模型转移方法研究

刘鑫鹏，秦玉华，张凤梅，蒋 薇，尹志豇

（1．青岛科技大学 信息科学技术学院，山东 青岛 266061；2．云南中烟工业有限责任公司技术中心，云南 昆明 650231）

近红外光谱分析技术可以快速高效地鉴定样品的化学组成和物质性质，分析过程不破坏样本、不污染环境，被广泛用于食品、农业、石化、烟草等领域［1］。在实际应用中，仪器间的台间差、外界环境的变化都会影响样品光谱的采集，导致对某台仪器建立的分析校正模型难以适用于其它仪器。若针对不同仪器、环境重新建立新的分析校正模型将消耗大量的人力和物力，难以满足网络化在线快速检测和分析的需求。目前解决这一问题最经济有效的方法是建立不同仪器之间光谱的转移模型，转移后的光谱可直接应用于现有的分析校正模型。该方法能够缓解重复建模带来的问题，节约建模成本，实现数据共享，尤其对近红外网络化的推广具有较大的应用价值［2］。

模型转移通过数学方法建立主机和从机所测光谱之间的函数关系，由确定的函数关系对光谱进行转换以实现现有模型的通用性［3］。袭辰辰等［4］将阿莫西林胶囊及其内容物光谱经分段直接校正（PDS）算法校正后，利用阿莫西林胶囊定量模型对校正后的光谱进行含量预测，通过探讨PDS中校正光谱和模型训练集中不同均质样本平均光谱的相似系数与预测误差的关系，寻找用于判定PDS校正准确性的量化指标；Zheng等［5］利用典型相关性分析（CCA）算法验证了光谱模型转移的效果；刘翠玲等［6］通过光谱空间转换法与多种方法，实现了模型转移后食用油酸值与过氧化值的分析。上述模型转移算法均为对光谱数据进行线性变化得到转移光谱。根据朗伯-比尔定律与加和定律［7］，样品的混合光谱应为其组成成分的纯光谱与对应浓度的乘积之和，但在光谱采集过程中，受环境因素的影响，获取的光谱往往掺杂了噪声，非线性误差将导致通过线性变换进行模型转移时光谱信息的丢失或重复。刘贞文等［8］采用深度自编码器的方法建立了不同仪器之间的非线性映射，作为一种非线性特征提取方法，其在药物片剂和玉米数据集上的模型转移效果优于传统线性光谱转移方法。但随着自编码器的加深，模型变得难以训练，产生梯度消失和过拟合现象［9］。

深度前馈神经网络作为一种应用广泛、发展迅速的人工神经网络，能够简单高效地拟合函数的特征映射，拥有复杂的非线性处理能力。由于光谱模型转移过程中，标样光谱样本的数量受到限制，网络各层的权值和阈值采用随机初始化，导致网络函数训练速度慢、拟合效果差。因此，本文引入麻雀搜索算法（SSA）对深度前馈神经网络进行全局参数优化。麻雀搜索算法是一种群智能优化算法［10］，通过模拟麻雀的觅食行为，求解参数的最优值，进而降低网络的复杂性。

本文基于麻雀搜索算法和深度前馈神经网络的优势，将两者结合用于近红外光谱的模型转移。以不同仪器采集的烟草光谱为研究对象［11］，建立主机与从机之间的非线性函数关系，并与传统的PDS、CCA方法进行了对比分析，验证了方法的有效性。

1 算法与原理

1.1 深度前馈神经网络

深度前馈神经网络（DFN）是一种基于前馈神经网络（FNN）的深度学习模型［12］。前馈神经网络通过定义一个函数映射，经多层神经网络的学习，调整网络中隐含层的连接权值和阈值参数，使非线性函数能够无限接近目标函数［13］，实现输入空间到输出空间的复杂映射。深度前馈网络架构如图1所示。本文利用深度前馈神经网络建立主机和从机所测标样光谱之间的函数关系，由确定的函数关系实现对烟叶光谱数据的转移，在已建立的光谱定性、定量分析模型下对转移后的光谱进行处理，提高了烟叶在线分析的效率。但深度前馈神经网络具有较深的网络架构，训练各层参数的权值和阈值需要消耗计算机大量的运行内存，增加时间成本投入。

图1 深度前馈神经网络结构Fig．1 Deep feedforward neural network structure

1.2 麻雀搜索算法

麻雀搜索算法是一种高精度、易扩充、自组织的智能优化算法，具有较高的全局寻优和求解能力［14］。通过模拟麻雀种群觅食的行为，在种群中设定发现者、加入者、侦察者3种身份的个体，通过叠加侦查预警机制，迭代更新群体觅食位置，以获得全局最优的觅食资源，从而获得参数的最优解。

在麻雀种群寻优过程中，发现者为种群寻觅高食物资源，引导加入者提供觅食方向，在安全区域内，通过位置记忆更新获取食物来源。在每次的迭代过程中，发现者的位置更新如下：

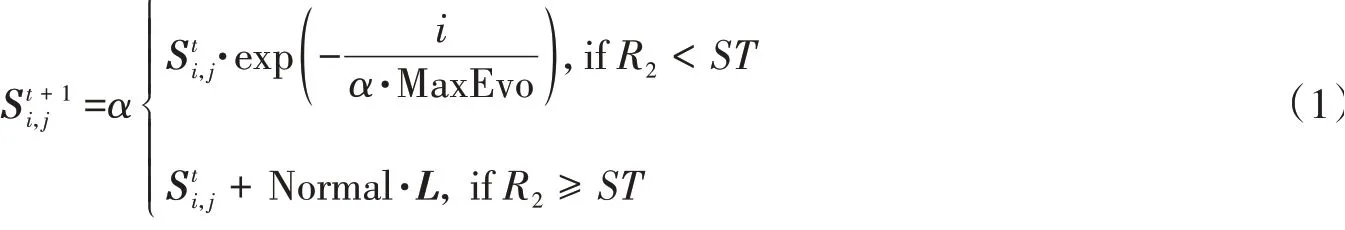
其中，t代表当前迭代次数，Si，j表示第i只麻雀在第j维中的位置，α为一个随机数，Normal是一个服从正态分布的随机数，L是1×d的矩阵，其内所有元素均为1。R2（R2∈［0，1］）和ST（ST∈［0．5，1］）分别表示预警值和安全值。R2≥ST表示位置安全可以搜索，反之发出预警并离开。

加入者通过侦听发现者位置处适应度值的高低选择位置觅食，当发现者处有较高食物资源时，加入者会离开当前位置前往发现者位置争夺资源，加入者位置变化如下：

Sposition是发现者所处的局部最优位置，Sworst表示全局最差的位置。A表示一个1×d的矩阵，每个元素随机赋值1或-1，且A+=AT（AAT）-1。当i＞n2时，表明第i个加入者仍未获得食物且适应度较低，需找寻其他位置获得食物资源。

侦察者为种群中发出预警更新安全区域的个体，其数量占种群的15%，位置更新如下：

Sbest是本轮迭代中的全局最优位置。β作为步长控制参数，是服从均值为0、方差为1的正态分布随机数。K是［-1，1］的一个随机数；fi、fb和fw分别表示当前麻雀的适应度、全局最优和最差适应度。ε是常数，避免分母为0。当fi＞fb表示麻雀所处位置易遭受捕食者攻击且正处于种群的边缘，当fi=fb时，表明麻雀意识到了危险，需要更新其位置降低被攻击的风险。

1.3 基于麻雀搜索算法结合深度前馈神经网络的光谱转移方法

本文使用麻雀搜索算法优化深度前馈神经网络的连接权值和阈值，利用深度前馈神经网络建立近红外光谱转移模型的步骤如图2所示。

图2 基于SSA-DFN建立光谱转移模型Fig．2 Establishment of spectral transfer model based on SSA-DFN

Step1：根据深度前馈神经网络的架构初始化麻雀种群数量（Population）和种群进化次数（MaxEvo）。以种群中容易找到食物的个体作为发现者，其他个体作为加入者，少部分为侦察者，随机初始化位置矩阵S，将优化后的位置矩阵作为深度前馈神经网络各层参数的初始值。计算个体所处位置食物资源的分配情况，即位置矩阵S个体的种群适应度（Fitness）。在深度前馈神经网络中，均方根误差Ek可以反映光谱转移的变化情况，因此使用均方根误差作为种群适应度的值，适应度函数表达如下：

Step2：麻雀种群数量是影响种群找寻食物资源的关键因素，为确定麻雀种群数量与优化算法性能之间的关系，将麻雀种群数量以6为间隔从20变化到140，以从机转移光谱与对应主机光谱之间的交叉验证均方根误差（RMSECV）作为评价参数，生成RMSECV与麻雀种群数量之间的关系图。如图3所示，随着种群数量增多，RMSECV逐渐降低，当种群数量为92时，RMSECV达到最低；种群数量超过92后，RMSECV逐步上升，因此将麻雀种群数量设为92。

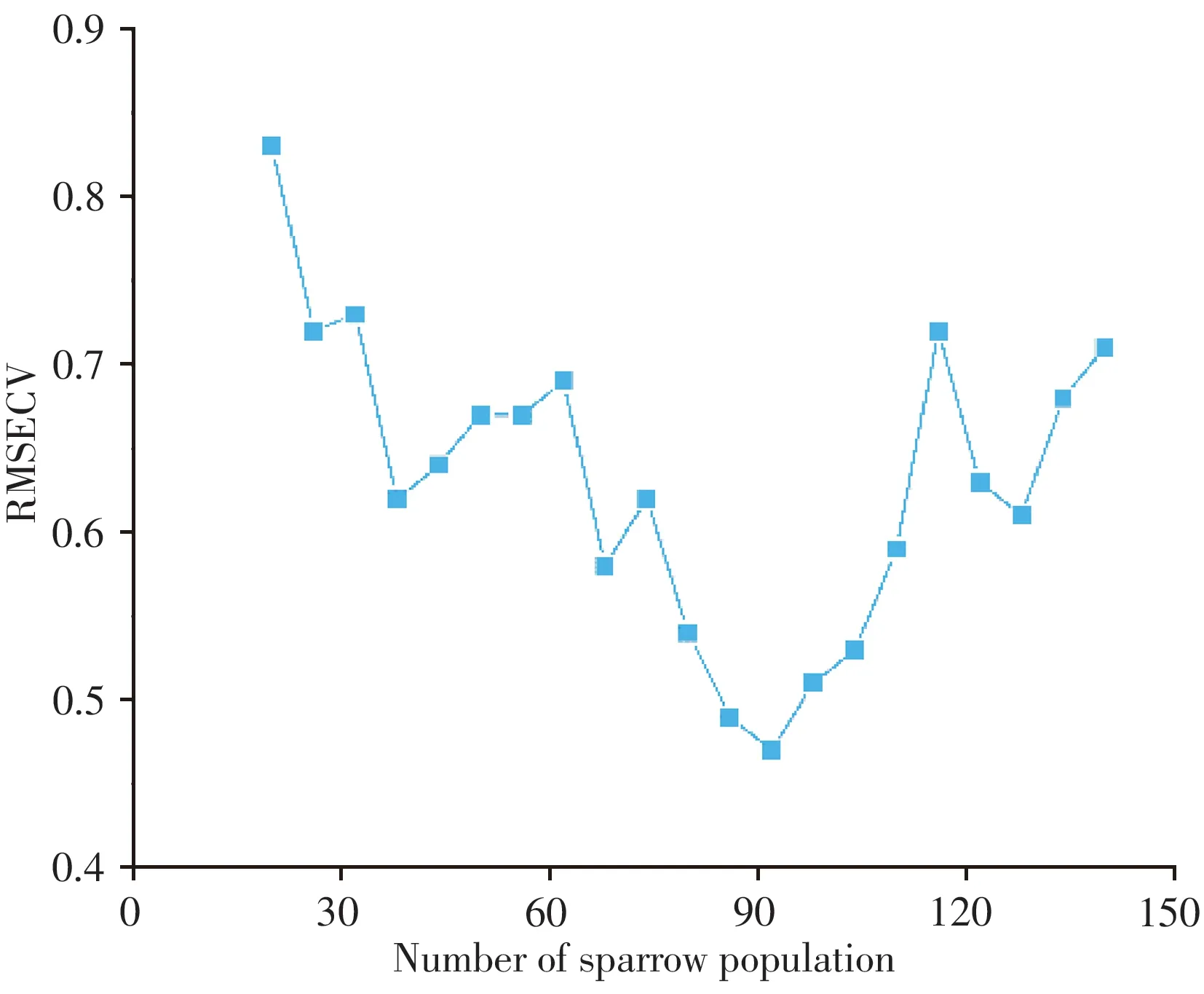
图3 RMSECV随麻雀种群数量的变化Fig．3 Variation of RMSECV with sparrow population

Step3：种群进化次数能够决定模型收敛的情况，使优化后深度前馈神经网络各层参数的初始值更容易训练。种群进化次数过少，麻雀搜索算法参数寻优结果不充分；种群进化次数过多，RMSECV达到一定水平后将不再变化，额外的种群进化将带来不必要的时间开销。如图4所示，种群进化次数从20变化到300，RMSECV呈阶梯式下降，当种群进化次数达210次后，RMSECV不再变化，说明麻雀种群个体位置已达全局最优解，模型的优化效果最佳［15］。

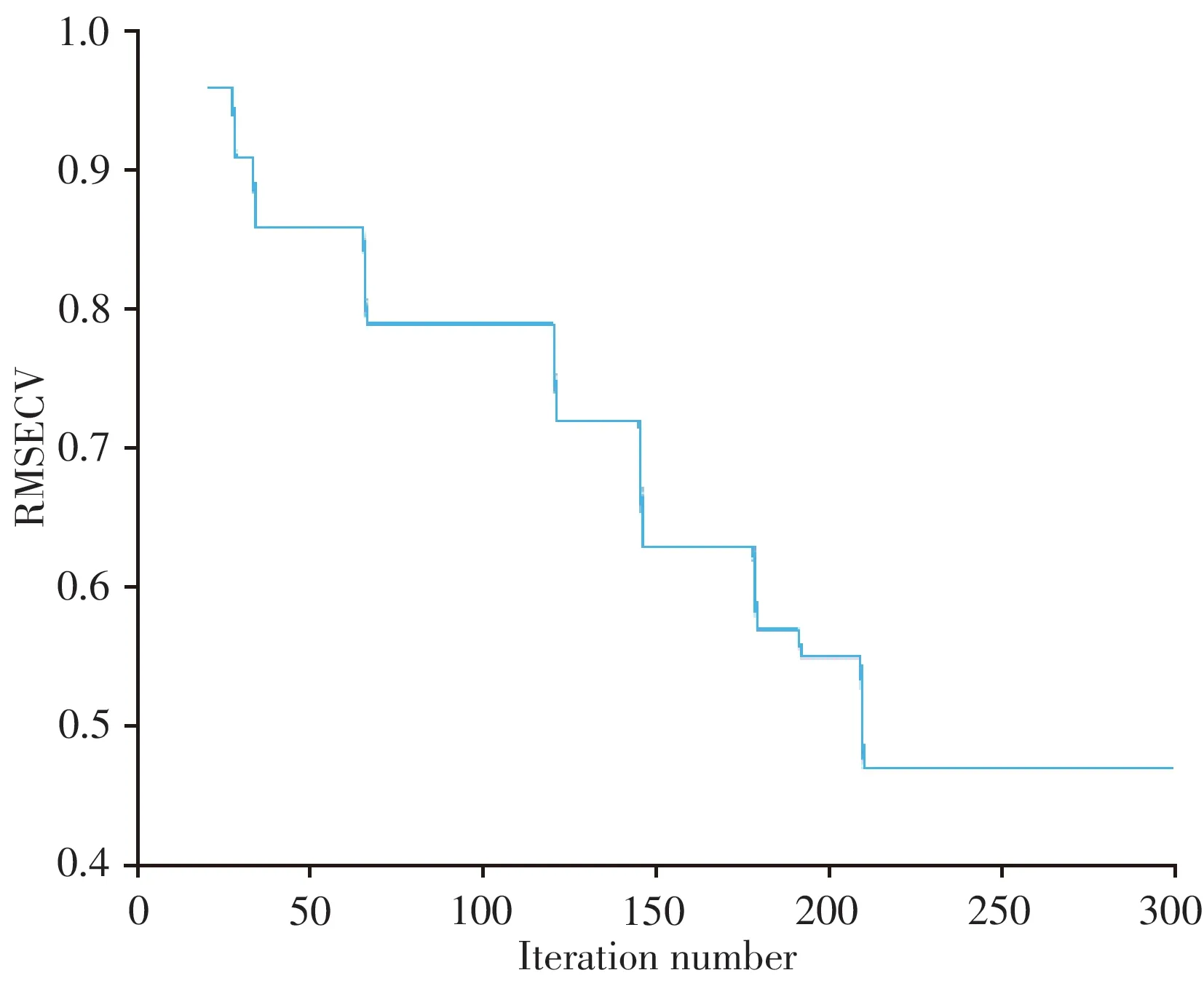
图4 RMSECV随麻雀种群进化次数的变化Fig．4 Variation of the RMSECV with the number of sparrow population iterations

Step4：分别采用公式（1）、（2）、（3）对发现者、加入者、侦察者进行位置更新，找寻更多的食物。调整个体身份，使觅食过程中加入者和发现者身份不断变化但所占比例不变，即当有一只麻雀变为发现者必然有一只麻雀变为加入者，种群个体在获取更多食物资源的同时躲避捕食者。

Step5：计算位置更新后种群中个体的适应度，根据种群个体适应度标记位置矩阵资源分配情况，并与原位置处的适应度进行比较，将适应度高的位置作为该个体的新位置。判定是否满足全局位置适应度最优或达到MaxEvo次种群进化，若满足则输出位置矩阵，否则重复执行步骤2、3，更新种群个体的位置信息与适应度。当麻雀种群处于安全区域内最优的觅食点，获取全局最优的位置矩阵，实现网络参数初始寻优。

Step6：对于给定光谱训练集Train=｛（x1，y1），（x2，y2），…（xn，yn）｝，xn∈Rd，yn∈Rd，输入从机光谱xi，输出对应的主机光谱yi，xi和yi皆为由d个波长点组成的实值向量。设在深度前馈神经网络中输入层包含n个输入量，输出层包含n个输出量，隐藏层包含q个神经元，建立7层神经网络模型，通过麻雀搜索算法初始化网络各层的权值和阈值。共优化8 092个参数，对经过迭代寻优后的种群位置矩阵S赋予网络各层权值和阈值。

Step7：深度前馈神经网络接收输入向量x，由前向传递函数计算得到输出结果ŷ并与对应的主机光谱y进行比较，再结合误差逆传播（BP）算法，更新网络中的连接权值和阈值大小。根据公式（5）、（6）实现数据前向计算：

其中，vit为输入层第i个神经元与隐藏层第t个神经元之间连接权值，ωtj为输出层第j个神经元与隐藏层第t个神经元之间连接权值；隐藏层第t个神经元的阈值用γt表示，输出层第j个神经元的阈值用μj表示。隐藏层第t个神经元接收到输入为αt，经过Sigmoid激活函数生成st；输出层第j个神经元接收到的输入为βj，经过激活函数生成从机预测转移光谱向量完成前向计算。在训练集上的均方根误差为：

Step8：基于梯度下降策略，以目标的负梯度方向对各层参数进行调整，直至均方根误差Ek达到一个较小的水平。在给定的学习率η下，根据下列公式调整连接权值ωtj、υit和阈值µj、γt：

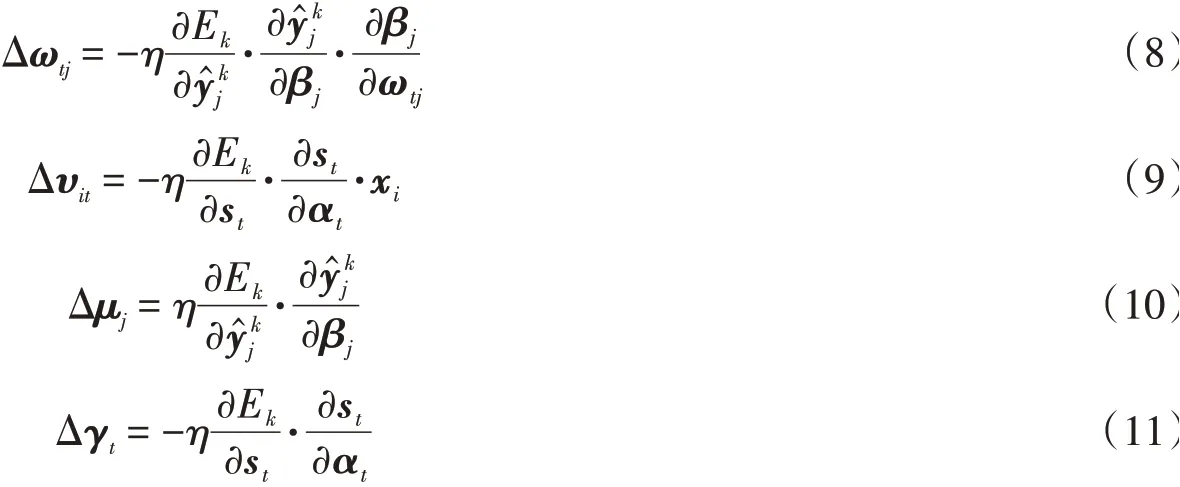
误差反向传播算法通过在每一轮的迭代中训练更新前馈神经网络每一层的连接权值与阈值，不断降低损失函数的值，使损失函数逐渐收敛，从而获取从机光谱与主机光谱的非线性函数映射，建立主、从机之间的光谱转移模型［16］。

2 实验部分

2.1 样品制备

选取某烟草企业提供的具有代表性的452个烟叶样品，置于60℃烘箱内2 h，磨碎过40目筛，常温避光密封保存24 h进行光谱采集。实验室温度控制在18~22℃、湿度＜60%。每个样品取20 g置于样本杯中用压样器压实，使用2台赛默飞世尔公司AntarisⅡ近红外光谱仪分别作为主机和从机进行光谱采集，光谱扫描范围为4 000~10 000 cm-1。为获得精准的光谱数据，每个样品在主机和从机上均重复扫描3次取平均值作为该样品的光谱。

2.2 光谱预处理与实验设计

样品的近红外光谱除包含自身的质量信息外，还承载了噪声、环境参数的影响。在建立校正模型前，选用Savitzky Golay（5，3）一阶导数进行预处理，以降低高频噪声、基线漂移和环境因素造成的影响。

以烟叶中总糖、总烟碱含量作为研究指标，选取315个主机和从机扫描的样品光谱作为训练集分别建立主机和从机的校正模型。另外选取25个不同产区、不同部位、不同等级、重复性好的样品作为模型转移的标准样品集，最终根据测试集均方根误差（RMSEP）确定模型转移最佳标准化样品个数，分别采用PDS、CCA、SSA-DFN 3种方法进行转移研究。剩余样品作为测试集，用来验证、对比转移方法的有效性。

3 结果与讨论

3.1 标准化样品数的确定

标准化样品个数的选取对模型转移的效果有一定影响，标准化样品数过多将造成数据冗余，过少则会使转移数据丢失，从而影响转移效果。图5为不同标准化样品个数下测试集总糖指标RMSEP的变化情况。

由图5可以看出，3种转移方法测试集的RMSEP均随标准化样品数的增多而降低，当标准化样品数为17个时RMSEP值最小，随着标准化样品数的继续增多，RMSEP值有所增大后趋于平稳，因此选定17个样品作为转移的标准化样品。

图5 不同标准化样品数下测试集总糖指标的RMSEPFig．5 RMSEP of total sugars in the test set under different standardized samples

3.2 转移光谱对比

图6为某烟叶样品主机、从机采集的光谱对比。可以看出，两台仪器的差异主要集中在4 900~5 700 cm-1，说明两台光谱仪器之间存在较为显著的非线性偏移。

图6 主机、从机的原始光谱对比Fig．6 Comparison of original spectra between master and slave

图7为采用PDS、CCA和SSA-DFN方法转移后的主、从机光谱对比。可以看出，3种方法转移后的从机光谱与主机光谱均有不同程度的重合，说明3种转移方法均具一定的效果。从全波段来看，SSA-DFN转移后的从机光谱与主机光谱重合度最高，在各个波数点处消除仪器间非线性偏移的效果较好，从机每个波数点的吸光度与主机基本一致，说明该方法能够有效对不同仪器光谱进行转移。

图7 转移光谱谱图对比Fig．7 Comparison of transferred spectra

3.3 光谱投影对比

利用主成分分析可将光谱数据降维，使新变量能够尽可能多地表达原始数据的特征。图8为分别采用不同转移方法后主机和从机测试样品的主成分空间分布图。

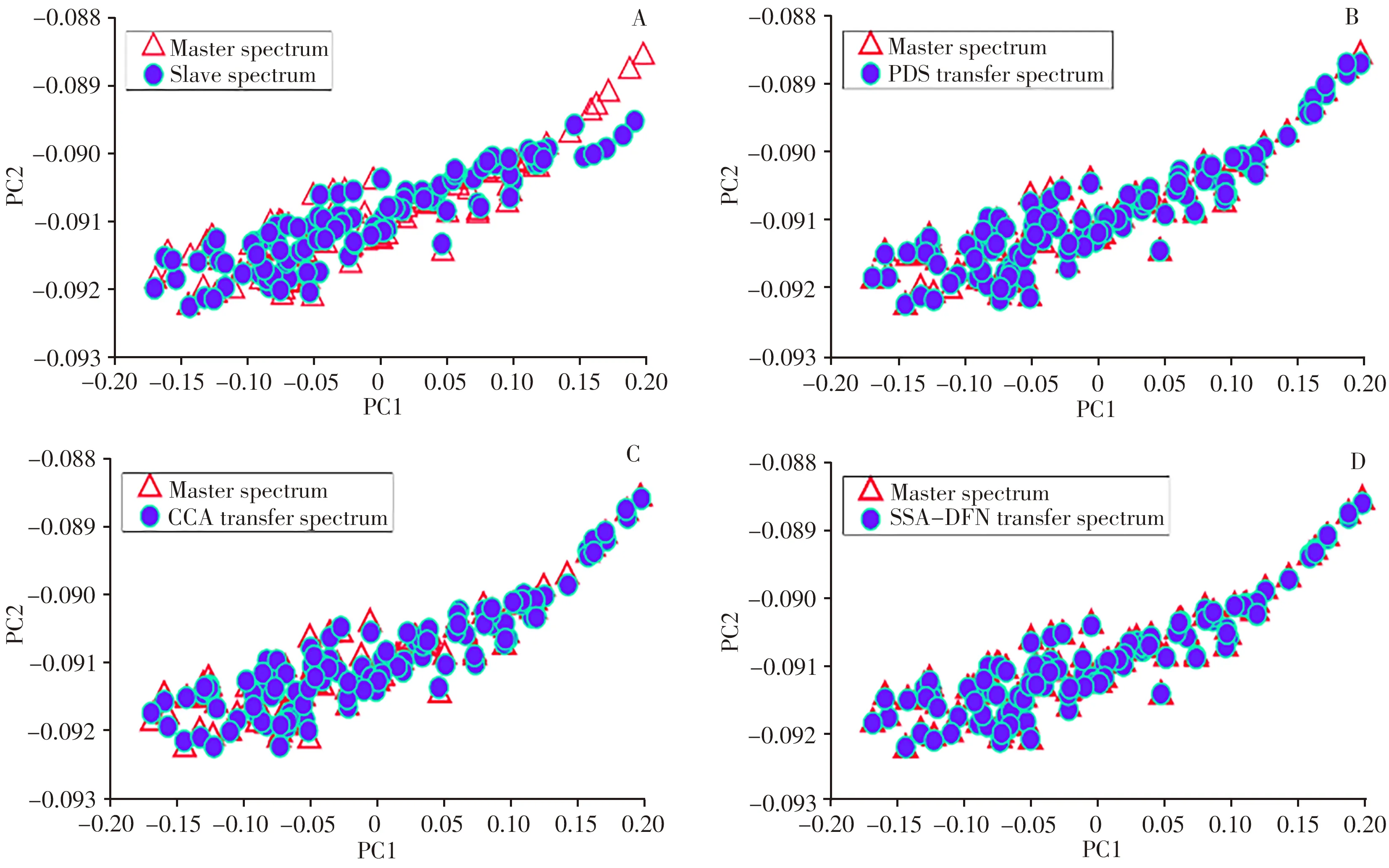
图8 不同转移方法光谱投影对比Fig．8 Comparison of spectral projection with different transfer methods

可以看出，转移前的主机光谱与从机光谱存在明显差异，经过PDS、CCA、SSA-DFN 3种方法转移后的从机光谱与主机光谱均有不同程度的重合。相比PDS、CCA方法，SSA-DFN转移后的光谱与主机光谱的投影重合度最高，说明转移后从机光谱与主机光谱所包含的数据特征最为相近，数据信息在转移后丢失率低，转移效果最佳。

3.4 预测结果对比

表1为不同的主、从机模型对不同测试集预测结果的对比。可以看出，直接使用主、从机模型分别对对应的主、从机测试集进行预测时，各项指标均达到较理想的效果，说明不同仪器建立的校正模型对本机采集的光谱适用度较高，单台仪器建模可以取得较好的效果。而使用主机模型对从机测试集、从机模型对主机测试集进行预测的误差均较大（高于5%），难以满足企业需求，且在t检验下（显著性水平α=0．05），主、从机模型对不同测试集的预测结果均存在显著性差异，说明主机和从机的台间差较大，主机模型无法适用于从机采集的光谱，需要进行模型转移。

表1 主、从机模型对不同测试集的预测结果对比Table 1 Comparison of prediction results between master and slave models for different test sets

表2为主机模型分别采用PDS、CCA、DFN、SSA-DFN 4种方法对从机测试集光谱转移前后总糖、烟碱含量的预测结果。可以看出，转移前主机模型对从机样品的预测误差较大，4种方法转移后的预测误差较转移前均有所降低。对于PDS、CCA、DFN方法，虽然模型转移后t检验差异不显著，但经PDS和CCA转移后光谱预测的总糖、烟碱平均误差高于5%，DFN转移后光谱预测的总糖平均误差为5．13%，均无法满足企业需求（低于5%）。SSA-DFN方法转移后总糖、烟碱预测误差分别降为4．65%和4．82%，t检验差异不显著，取得较好的转移效果，该结果与基于谱图及光谱投影的结果一致。

表2 不同转移算法预测结果对比Table 2 Comparison of prediction results of different transfer algorithms

4 结论

为提高不同仪器之间光谱模型转移的准确性，本文提出了基于麻雀搜索算法结合深度前馈神经网络的模型转移方法SSA-DFN，在谱图、光谱投影以及建模效果等方面均取得了较优的实验结果，证明SSA-DFN是一种稳定、高效的非线性模型转移方法。将深度前馈神经网络用于拟合模型转移的映射函数，并利用麻雀搜索算法优化神经网络，可使网络训练变得容易且高效。通过SSA-DFN方法对光谱进行模型转移，将一台仪器上建立的模型应用于其他仪器，一定程度上满足了网络化快速分析的需求，减少了重复建模的额外开销，提高了已有模型的利用率。