基于免疫算法结构分解的分布式预测控制算法
刘臻博,金 鑫,李 平
(辽宁石油化工大学 信息与控制工程学院,辽宁 抚顺 113001)
模型预测控制(MPC)[1]作为一类基于计算机控制的算法,因其控制性能良好、鲁棒性强的特点,越来越多地被应用在流程工业中[2]。随着工业过程的日益复杂,传统的集中式预测控制难以满足其控制性能的要求[3]。因此,提出了分散式预测控制算法,将大系统转化为若干个相互独立的子系统再进行求解[4‐5]。这种算法的优势在于结构简单、控制器之间无需通信,但当各子系统之间的耦合影响比较强烈时,分散式控制系统就无法达到满意的控制性能[6‐7]。近年来,随着计算机网络技术的创新与发展,分布式模型预测控制(DMPC)应运而生,并且得到了广泛的关注与研究。
A.Conley等[8]基于雅可比方法引进了合作式DMPC算法[9],该算法能够有效地解决输出反馈下耦合输入约束的问题,但不能保证算法收敛速度。针对系统间通信问题,刘袁龙[10]提出了一种基于层次分解的DMPC算法,将子系统划分在不同的连通集内,在求解时,子系统只与连通集内的子系统通信,再将控制信息传入下一连通集,从而有效地减少各个子系统间的通信次数。
以上研究在解决DMPC算法中存在的收敛速度不够、通信复杂、稳定性条件复杂等问题时,很少考虑到系统分解对这类问题的影响,系统分解方式可以有效缓解系统间通信负担,还能提升DMPC在线实施效率[11]。针对DMPC的系统分解存在动态预测耦合的问题,文献[12—13]提出了一种基于遗传算法(GA)的分布式预测控制系统结构分解方法,该方法分为输入分组(ICD)和输入输出配对(IOPD)两个阶段,并采用GA算法来求解这一组合优化问题,从而有效地减小子系统之间的耦合,提高DMPC算法的效率。但是,GA算法作为一种一般的寻优算法,存在局部搜索能力差和“早熟”等缺陷,不能保证算法收敛速度,同时该方法不能有效解决子系统之间一些无法消除的耦合问题。
本文提出一种基于免疫算法(IA)求解系统结构分解的分布式模型预测算法。该方法分为两个部分。第一部分沿用文献[13]的方法,将系统结构分解问题分成ICD和IOPD两个阶段来求解,并采用IA算法来优化这两个阶段的目标函数。IA算法是一种带有全局搜索能力的优化算法,具有自适应性、随机性、种群多样性的特点,能够克服一般寻优过程中不可避免的“早熟”问题。第二部分采用DMPC算法,在约束条件下对分解后的系统进行分布式控制。最后,对重油分馏化工过程进行实验研究,验证该方法的有效性。
1 基于IA的DMPC系统分解
分解大系统时需要考虑ICD和IOPD两个问题。ICD是找到每个子系统对应的输入问题;IOPD是解决ICD问题后,根据得到的每个系统对应的输入再考虑对应的输出问题。
1.1 ICD问 题 与IOPD问 题
1.1.1 ICD问题 根据文献[13],定义一个输入分组矩阵H和一个表示子系统间耦合程度的目标函数Jcoupling,矩阵H定义为:
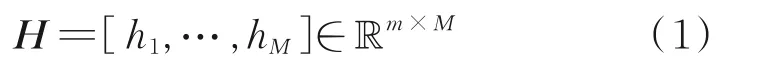
式中,m为子系统的个体数量;M为子系统的个数,满足M≤m。矩阵H满足:

子系统间系统耦合程度的目标函数定义为:

通过求解最小化Jcoupling,对给出的大系统的输入进行分组。
1.1.2 IOPD问题 ICD问题已经将系统的输入分成M个子系统,IOPD问题的目标是找到各子系统中输入对应的输出,与式(1)输入分组矩阵类似,定义一个输出分组矩阵H′为:

矩阵H′应该满足:

子系统间输入输出耦合程度的目标函数定义为:
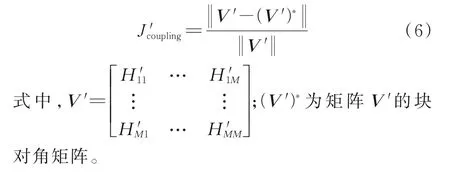
通过求解最小化J′coupling,对系统输入输出进行配对。
1.2 基于IA的分布式模型预测控制系统分解
求解ICD问题和IOPD问题,实质上就是求解式(3)和式(6)的过程。矩阵H和矩阵H′中的元素都为0或1,采用免疫遗传算法(IGA)[14]来求解。因为免疫遗传算法源于遗传算法,很容易对0和1进行编码。
为了把IGA应用到目标函数的求解过程中,需要对编码、免疫选择、克隆、变异等IGA的操作进行重新定义。
1.2.1 应用IGA求解ICD问题
(1)编码。用一个二进制的具有M个子系统的行向量来表示每个抗体,即表示系统输入的分组情况。例如,将一个八输入的系统分为两个组(子系统),分组情况可以表示为:

其中,输入1—4分到子系统1中,输入5—8分到子系统2中。每个抗体的染色体可以分为M个组中,相应位置上的变量1表示该输入被选入当前小组。
(2)初始种群。初始种群就是抗原识别后产生的初始抗体种群。每个种群都要满足相应的约束条件,即每个输入只能存在于一个小组中。
(3)亲和度函数。亲和度表示免疫细胞(如B细胞)与抗体的匹配强度。在产生种群之后,每个抗体作为亲和度函数的输入,输出即为亲和度评价结果。针对最小化问题(3),抗体的亲和度函数可以写成目标函数的倒数:
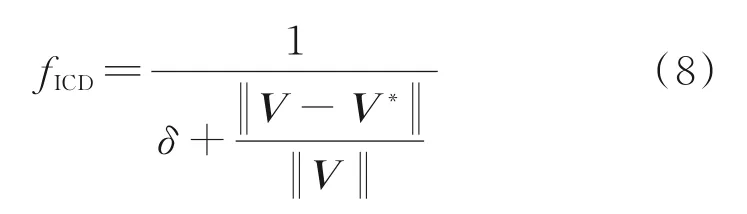
式中,fICD为ICD问题的目标函数;δ为一个不为0的小数,保证公式的分母不为0。可见,目标函数越小,亲和度函数越大。
(4)抗体浓度函数。抗体浓度表示产生抗体形成的种群多样性优劣程度。抗体浓度过高,说明种群中类似的抗体大量存在,使寻优搜索局限化。因此,在IGA算法中需要对浓度过高的抗体进行处理和抑制,从而确保抗体在种群中的多样性。抗体浓度通常定义为:

式中,N为抗体种群规模;S(ai,aj)为抗体间的相似度,可以表示为:

式中,ai、aj分别为种群的第i及第j个抗体;ξs为相似阈值;α(ai,aj)为抗体i与抗体j的亲和度,即对0−1编码的算法,抗体与抗体间亲和度基于海明距离的计算方法进行求解。基于海明距离的抗体‐抗体亲和度计算方法的表达式为:
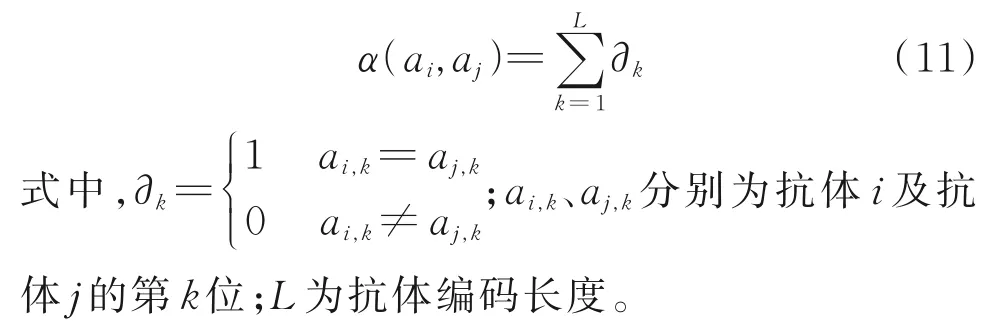
(5)激励度函数。抗体激励度函数是对抗体质量的最终评价结果,其目的是为了保留亲和度大、浓度低的抗体。抗体激励度函数可以表示为:
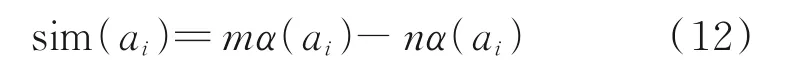
式中,sim(ai)为抗体ai的激励度;n为计算参数。
(6)克隆。由抗体激励度来决定哪些有效抗体能进行克隆选择操作,在抗体种群中激励度高的有效抗体具有更好的品质,大概率会被选入克隆选择工作。克隆函数可以表示为:

式中,clone(ai)为wi个与ai相同的克隆抗体的集合,wi为抗体克隆数目。
(7)变异。变异操作是为了扩展搜索寻优的空间,从而产生一个新的抗体。对于0−1编码IGA算法,其变异策略是从变异源抗体中随机选取一个或多个位置取反。这里定义的变异就是将抗体中某个表示相应输入位置的变量1置换为0,剩余的其他相应位置0置换为1。例如:
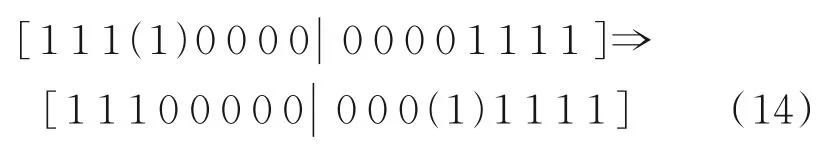
其中,子系统1中括号内变量1置换为0,表示输入4不包含在子系统1中,那么在子系统2中相应的第4个位置的变量0置换为1,表示输出4包含在子系统2中。
在求解最小化问题(3)的寻优过程中,免疫选择、克隆、变异都能产生新的抗体,需要不断迭代这些操作来最终满足一个收敛条件,从而得到一个最优解H∗,进而构造ICD问题的最优分组矩阵。
1.2.2 应用IGA求解IOPD问题 在IOPD问题中,IGA的操作基本与ICD问题相同,只在编码和亲和度函数的定义上略有不同。
(1)编码。用一个具有M个数的二进制的向量表示抗体,即表示系统输入输出配对的状态。一个六输出的系统被分为3个组,那么分组情况可以表示为:

其中,输出1和输出2被分到子系统1中,输出3和输出4被分到子系统2中,输出5和输出6被分到子系统3中。总的来说,每个抗体的染色体可以被分为M个子系统,相应位置上的变量1表示该输出被选入当前小组。
(2)亲和度函数。针对最小化问题(6),抗体的亲和度函数可以写成目标函数的倒数。

式中,fIOPD为IOPD问题的目标函数。
根据式(16)可知,分母即目标函数越小,亲和度函数越大。
当求解IOPD问题后,得到的最优解可以表示为IOPD的最优分解矩阵(H′)∗。
因此,ICD问题和IOPD问题都得到相应的解决,从而得到两个分组矩阵,即和(H′)∗=[(h1′)∗,…,(hM′)∗]。
2 分布式模型预测控制
针对多个子系统间存在无法消除的耦合问题,需要采用DMPC算法来解决。在系统结构已经分解完成的前提下,介绍DMPC中各子系统的状态空间预测模型以及基于IGA系统结构分解的DMPC算法实现流程。
2.1 DMPC控制器设计
一个包含M个子系统的分布式系统S,其子系统Si(i=1,…,M)的状态空间模型为:
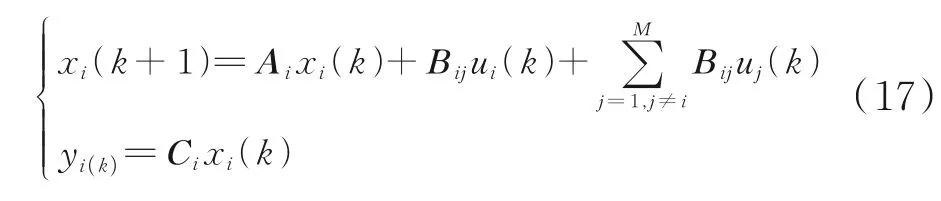
式中,Ci为输出矩阵;Ai为系统矩阵;Bij(i≠j)为子系统Sj对子系统Si的耦合输入矩阵;uj为子系统Sj在k时刻的输入序列。
对k时刻子系统的状态向量及输出向量进行预测,由式(17)表示的模型可以推导出以下矩阵‐矢量形式:

式中,Xi(k)为状态变量的集合;ηi为系统矩阵的集合。

式中,Ui(k)、Uj(k)为控制变量的集合。令:

结合式(22),目标函数(23)的最优解问题可以写成:
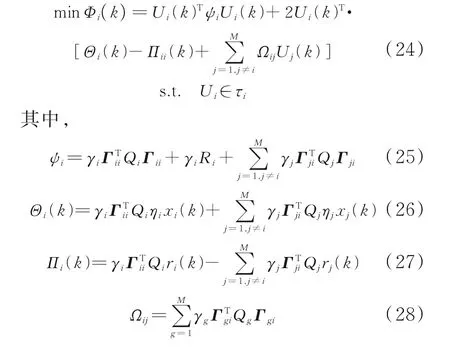
子系统i在k时刻的最优控制序列Ui由二次规划算法求解得到。
2.2 基于IGA系统结构分解的DMPC算法实现流程
提出了基于IGA系统结构分解的DMPC算法,其具体实现流程为:
步骤1给定具有m个输入和p个输出的大系统,在已知系统需要被分为M个子系统的前提下,利用IGA算法求解目标函数式(8)的最大值,从而解决ICD问题,得到最优输入分组矩阵H∗;根据最优输入分组矩阵H∗,利用IGA算法求解目标函数式(16)的最大值,从而解决IOPD问题,得到最优输入输出配对分组矩阵(H′)∗。根据求解的结果,确定每一个子系统中输入输出的数量。
步骤2在k时刻,获取每一个子系统i的状态空间模型和输出方程式(17),并给定抗体种群规模N、状态变量权值Qi、控制变量权值Ri、权重γi、系统控制变量的初值ui,0(k)。
步骤3子系统i将控制变量通过网络传递给其他子系统,同时获取其他子系统的控制变量。
步骤4并行求解采用迭代求解方式。在迭代时刻q(q≥1),根据式(19)—(22)和式(24)—(28),在满足约束条件的情况下并行求解各子系统最优控制序列(k),给定收敛精度ξ及迭代最大次数qmax。若各子系统控制输入均满足不等式或迭代次数满足q>qmax,则进入步骤5;否则,令q=q+1,转步骤3。
步骤5取子系统的最优控制序列(k)的第一项为控制输入:
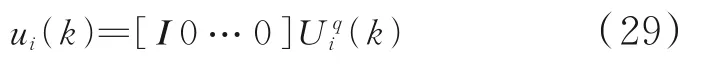
式中,I为单位矩阵。将式(29)应用于各子系统。
步骤6令k=k+1,并将上述控制变量求解过程滚动优化到下一时刻,返回步骤2。
3 仿真研究
以重油分馏塔模型为对象,验证所提IGA‐DMPC算法的有效性[15]。重油分馏塔模型如图1所示。

图1 重油分馏塔模型
图中,T为回油口;A为出油口;LC为液位控制器;PC压力控制器;FC流量控制器。控制过程中的输入变量:顶部采出u1、侧线采出u2、中部回流量u3、顶部回流量u4。输出变量:顶部产品干点y1、侧线产品干点y2、中部回流温度y3、顶部回流温度y4。系统的模型为:

3.1 DMPC系统分解问题
3.1.1 ICD问题 已知系统有4个输入,给定系统被分为2个子系统,预测时域为K=20,采样时间Ts=1 s。输入输出的权重矩阵分别为Q=I和R=I。每一代抗体种群NIND=30,最大代数GENMax=100,免疫选择抗体数量为15,变异发生的概率为0.5,克隆个数为10。
ICD分解每代最优目标函数曲线如图2所示。由图2可以看出,分解目标函数的初代的起始亲和度为1.060,在经历4代以后最优亲和度为0.850。

图2 ICD分解每代最优目标函数曲线
ICD分解每代的最优亲和度的分组情况图3所示。图中,两种颜色表示两个小组。
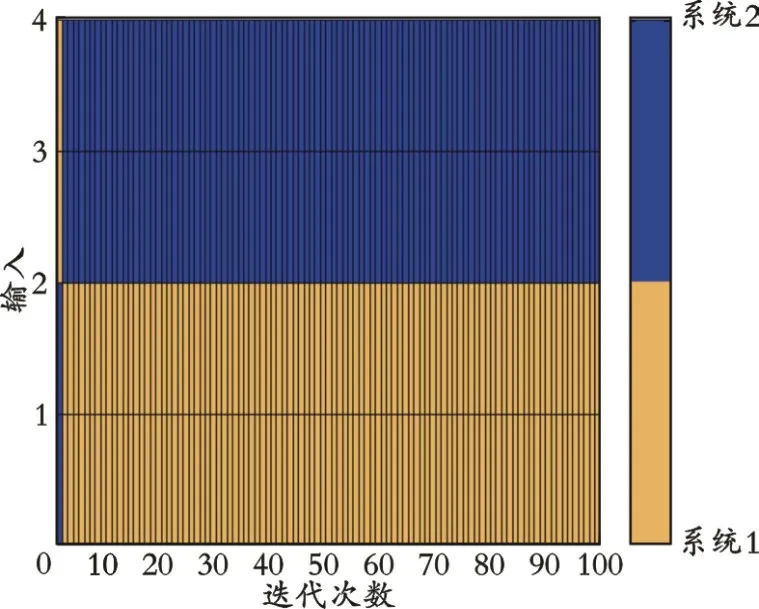
图3 ICD分解每代的最优亲和度的分组情况
最终得到的分组情况可以用0−1向量表示为:

输入1−2被分为一组,输入3−4被分为一组。
3.1.2 IOPD问题 完成输入分组后,对IOPD问题进行求解。根据式(30)输入分组的结果,输入分组矩阵H可表示为:

由此矩阵求解IOPD问题得到输入输出配对的分组矩阵H′。IOPD分解每代最优目标函数曲线如图4所示。由图4可以看出,分解目标函数的初代起始亲和度为0.455,经历4代以后最优亲和度为0.436。
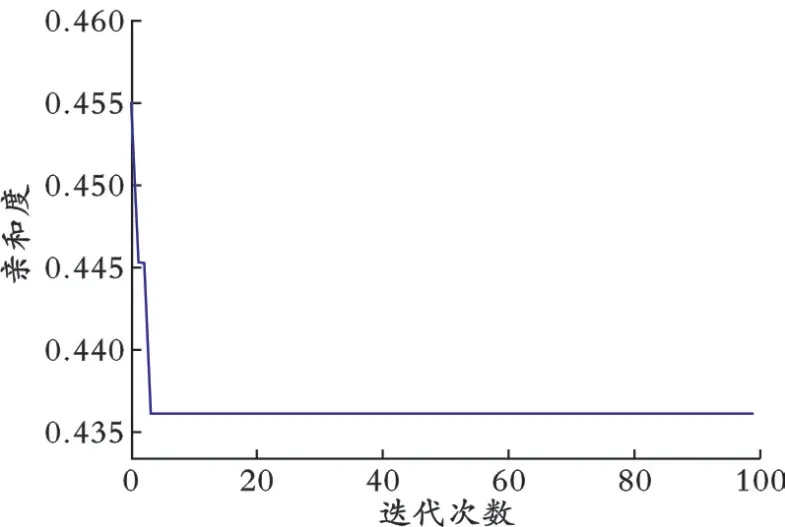
图4 IOPD分解每代最优目标函数曲线
IOPD分解每代的最优亲和度的分组情况如图5所示。
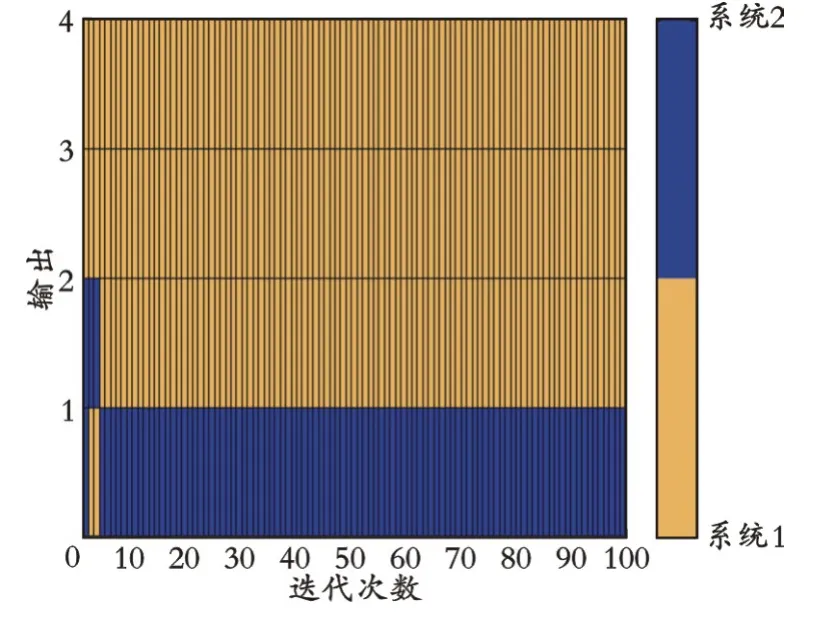
图5 IOPD分解每代的最优亲和度的分组情况
最终得到的分组情况可以用0−1向量表示:

根据式(32)输出分组的结果,输出分组矩阵H′表示为:

根据矩阵H和H′,系统的输入输出最终配对可以表示为:
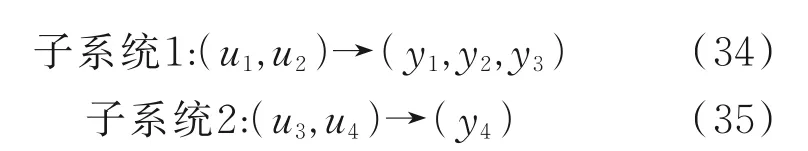
3.2 基于DMPC算法的分解后系统的分布式控制
已知重油分馏过程的系统结构被分解为分别含有输入1−2、输出1−3的子系统1和含有输入3−4、输出4的子系统2。采用DMPC算法对分解后的系统进行分布式控制,主要控制参数为:
(1)采样时间Ts=1 s。
(2)N=200,M=5,预测时域P=20。
(3)各子系统中的权重矩阵Ri为单位矩阵,矩阵Qi的取值为:

式中,qi=I;q∗i为终端加权矩阵,目的是确保该控制子系统的稳定性。
(4)在DMPC仿真中,两个子系统的权重分别为γ1=0.8、γ2=0.2。
(5)各子系统Si的优化命题为:
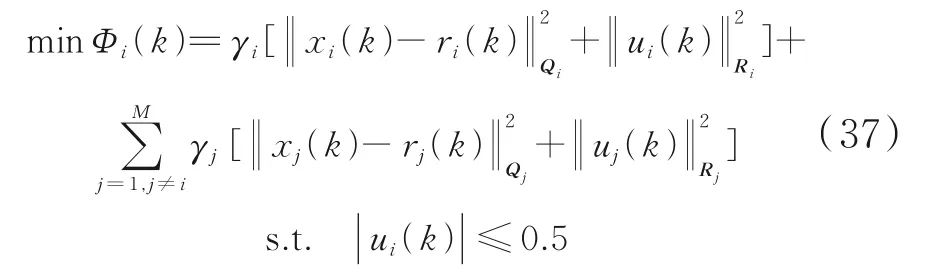
IGA‐DPMC算法子系统的输出及输入曲线如图6−7所示。集中式MPC算法子系统的输出及输 入 曲 线 如 图8−9所 示。图6−9中,下 标i为1、2、3、4。
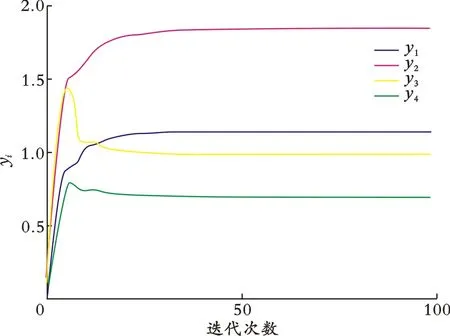
图6 IGA‐DPMC算法子系统的输出曲线

图7 IGA‐DPMC算法子系统的输入曲线

图8 集中式MPC算法子系统的输出曲线
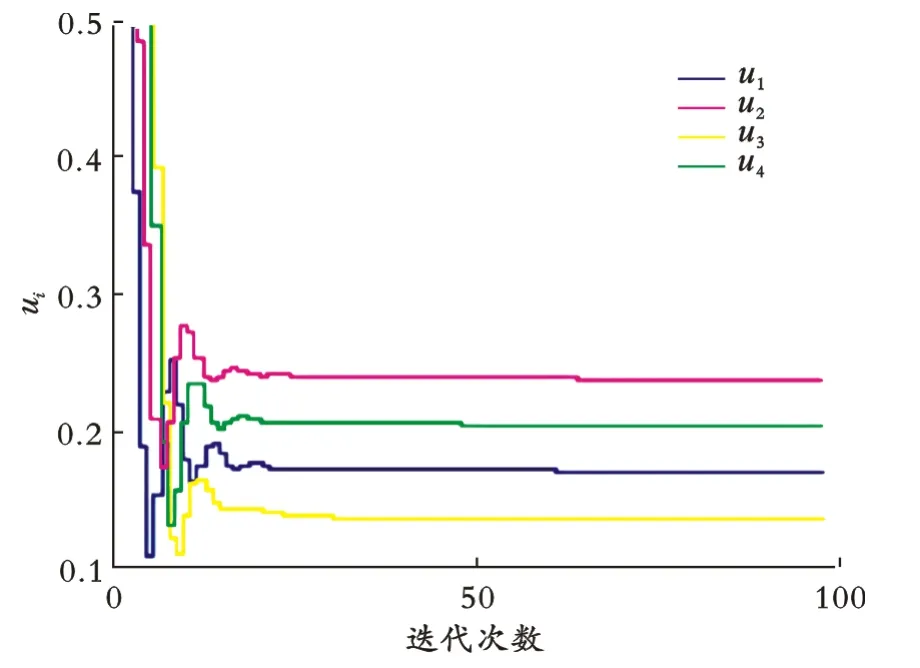
图9 集中式MPC算法子系统的输入曲线
为了更好地对比两种算法的控制性能,以顶部产品干点为分析数据,引入最大超调量、上升时间、平均迭代时间为指标进行分析。CMPC和IGA‐DMPC控制性能如表1所示。

表1 CMPC和IGA‐DMPC控制性能
由图6−9及表1可以看出,IGA‐DMPC算法在重油分馏过程中有很好的控制效果。例如,子系统1的顶部采出量和侧线采出量对反应器中顶部产品干点、侧线产品干点和顶部回流量有至关重要的作用;子系统2的中部回流量和顶部回流量对中部回流温度有很大作用。在IGA‐DMPC算法中,相关联的信息都在各子系统内部进行交换,大大减小了系统的通信负担,而CMPC算法没有考虑到系统中控制量彼此之间的相互作用。在控制效果大致相同的情况下,IGA‐DMPC算法的迭代时间明显少于CMPC算法,大大提高了工作效率。综上,采用本文提出的算法可以更有效地控制实际的化工过程。
4 结 论
近些年来,DMPC算法得到了广泛关注和研究。但是,以往研究在DMPC算法中子系统间存在强烈耦合影响时,很少考虑到将系统结构分解结合到DMPC算法中。所提方法首先采用IA算法对DMPC系统进行结构分解,再利用DMPC算法对分解后的系统进行分布式控制。为了解决系统结构分解的问题,对IA中的编码、免疫选择、变异、克隆等操作进行了重新定义。通过仿真研究,验证了算法的有效性。在未来的研究中,考虑将本算法应用到非线性的DMPC系统中。

