双圆盘含裂纹转子系统振动特性探究

高天宇，高 鹏，王立军

（1.辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001；2.抚顺新钢铁有限责任公司，辽宁 抚顺 113001）

旋转机械广泛应用于许多行业和工程领域。转子系统是旋转机械的核心部件，其可靠性决定旋转机械的质量。由于机械在加工过程中不可避免地存在一些缺陷，而且转子系统在工作中长期受到载荷、扭矩和腐蚀等因素的影响，一些转轴比较容易出现裂纹。转子裂纹是旋转机械的一种常见的故障，由于裂纹的存在，整个转子系统的非线性行为更加复杂，会导致设备的异常振动，情况严重时疲劳裂纹会进一步扩展，引起设备损坏，造成巨大的经济损失。因此，开展裂纹对转子系统的影响尤为重要。

对裂纹转子的动力学特性，大多数学者还是以Jeffcott模 型 为 基 础 进 行 研 究[1]。A.K.Darpe等[2‐3]推导了完整的柔度矩阵，分析了裂纹转子的振动特性及裂纹开闭规律。同时，研究了含横向裂纹的Jeffcott转子在轴向激励作用下的响应特性，采用线性断裂力学中的应变能量释放率理论计算裂纹转子刚度，利用应力强度因子为零模型中的裂纹闭合线位置模型（CCLP）模拟裂纹的呼吸作用。A.S.Sekhar等[4‐5]研究了裂纹检测和监控，并对比了直裂纹与斜裂纹转子的不平衡响应特性，分析了裂纹转子通过其临界速度时的瞬态振动响应。P.N.Saavedra等[6]通过线性断裂力学计算了裂纹引起的附加柔性，应用应力强度因子为零的方法建立了呼吸裂纹转子动力学模型，在Matlab平台上求解了运动方程并进行了实验验证。结果表明，2X成分（二倍工频）以及1/2一阶临界转速附近的轴心轨迹可作为裂纹检测的重要指标。进入21世纪以来，对裂纹转子系统的研究不再局限于简单的理想状态，耦合故障、复杂支承等多种因素也被考虑进来，同时诊断技术也更加全面。向玲等[7]基于轴心轨迹的形态，对裂纹与碰摩的耦合故障进行研究，并进行了实验对比。万方义等[8]分析了非线性油膜力作用下裂纹转子的动力学特性，并将此结果与刚性支承情况进行了对比。刘桂珍等[9]建立了非稳态油膜力作用下的裂纹转子力学模型，应用数值仿真的方法计算了偏心量变化时的非线性动力学行为，揭示了系统分岔特性和进入混沌的途径。张星雨等[10]假设裂纹深度不变，在现有Jeffcott转子模型的基础上加入裂纹扩展变量，将裂纹扩展与转子振动耦合，观测了裂纹扩展中的动力学特性以及影响裂纹扩展速度的因素。文献[11−14]使用有限元分析软件ABAQUS，对裂纹转子动力学特性以及裂纹诊断进行了进一步研究。刘明岳等[15]基于J2积分和材料力学中的弯曲理论，探讨了六棱柱结构的横向裂纹，给出了求解复杂结构应力强度因子的一个方法。

本文根据Jeffcott转子动力学模型，结合断裂力学理论，建立了裂纹转子系统的有限元模型，并对不同裂纹深度、裂纹角度和不同转速进行了仿真分析，从时域图、频域图和轴心轨迹图三个角度对不同裂纹参数的裂纹转子系统振动特性进行了探究。然后，采用机械综合故障台对部分裂纹转子进行实验分析，将实验结果与仿真数据进行对比，验证了仿真及建模的结论。

1 裂纹单元刚度矩阵及转子系统动力学方程

1.1 裂纹单元刚度矩阵

转子裂纹单元模型示意图如图1所示。图1中，l为裂纹单元长度；N1、N7为轴段所受的轴向力；N2、N3、N8、N9为剪力；N4、N10为扭矩；N5、N6、N11、N12为弯矩。

图1 转子裂纹单元模型示意图

由Castingliano定理可得裂纹单元各自由度的位移：

式中，U=U0+Uc；U为裂纹单元总应变能，J；U0为无裂纹轴单元应变能，J；Uc为裂纹引起的附加应变能，J；Ni为外力，N；ui为节点自由度上的广义位移，mm；为无裂纹轴单元位移，mm；为裂纹引起的附加位移，mm。

考虑轴向力、扭矩、弯矩以及裂纹截面的剪切效应，无裂纹轴单元应变能U0为：

式中，V1、V2分别为无裂纹轴单元所受水平与竖直方向上的剪切力，N；M1、M2分别为无裂纹轴单元所受水平与竖直方向上的弯矩，N·m；T为扭矩，N·m；F为轴向力，N；E为材料的弹性模量，MPa；Ip为极惯性矩，m4；A为圆截面面积，m2；αs为剪切系数；Iz为横截面惯性矩，m4；Ge为切变模量，MPa。此时，载荷为轴单元局部载荷，根据单元力和力矩平衡可得式（3）。

无裂纹单元体柔度为：

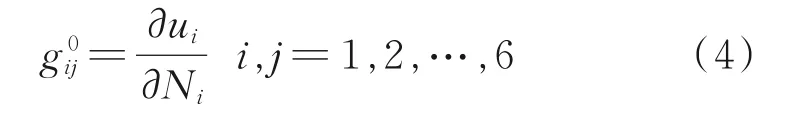
根据断裂力学理论，由裂纹扩展引起的附加应变能为：

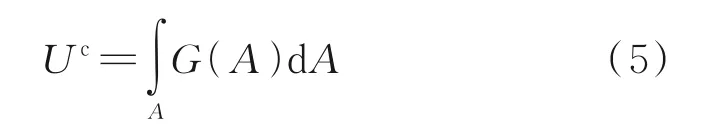
式中，G(A)为应变能密度函数，其表达式为：

式中，Ni、Nj均为外力，i,j=1,2,…,6，N。

由式（4）、式（7）可得裂纹单元体的柔度矩阵：

该柔度矩阵为对称矩阵，将其整合到裂纹转子系统的模型中，便可得到裂纹轴的刚度矩阵。由静平衡条件知：

可得转换矩阵：

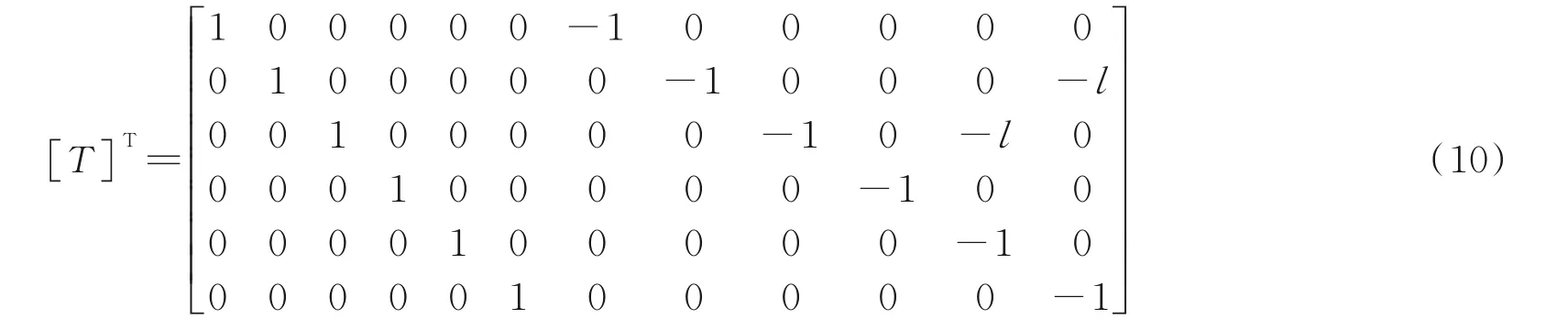
裂纹单元刚度矩阵为：

1.2 裂纹转子系统动力学方程

在静止坐标系下，裂纹转子系统的动力学方程为：

2 裂纹转子系统的振动特性仿真分析

为了进一步了解裂纹转子系统的振动效果，在建立动力学方程的基础上，对系统以恒定转速运行时的稳定工况进行分析。通过仿真计算得到系统上某一点的时域、频域和轴心轨迹曲线；增加裂纹深度、改变裂纹倾斜角度（裂纹角度，下同）、调整系统的运转速度（转速，下同），分析上述参数对裂纹转子系统振动响应的影响，探究其内在规律。

有限元模型的参数与实验条件保持一致。裂纹转子系统的基本参数为：转轴直径d1=18.8 mm，长度l1=860.0 mm，材料为45#钢，密度ρ1=7 850 kg/m3，弹性模量E=206 GPa，泊 松比v=0.3，两个圆盘各自距离轴两侧250.0 mm，直径d2=150.0 mm，厚度l2=10.0 mm，密度ρ2=2 700 kg/m3。转子系统模型示意图如图2所示。

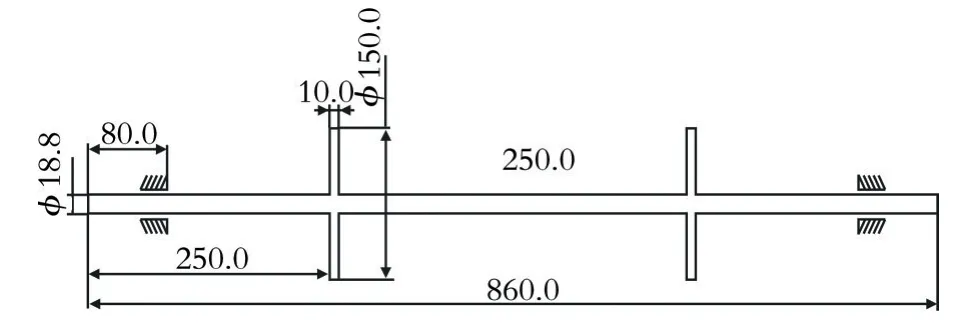
图2 转子系统模型示意图（单位：mm）

2.1 裂纹深度对转子系统振动的影响

在实际工程中，裂纹的出现会使转子系统的振动特性发生改变。当系统受到较大的交变载荷时，裂纹会迅速扩展产生疲劳失效，导致系统可靠度降低。因此，研究裂纹深度对动力学特性的影响具有重要意义。在转轴正中部建立裂纹深度比（用裂纹深度与转轴半径之比即裂纹深度比表示裂纹深度）分 别 为0.3、0.5、0.7、1.0的 直 裂 纹，设 置 转 速 为1 200 r/min，通过仿真分析得到振动曲线图。不同深度裂纹转子系统的时域图及频域图（仿真结果）如图3所示，其轴心轨迹（仿真结果）如图4所示。

图3 不同深度裂纹转子系统时域图及频域图（仿真结果）

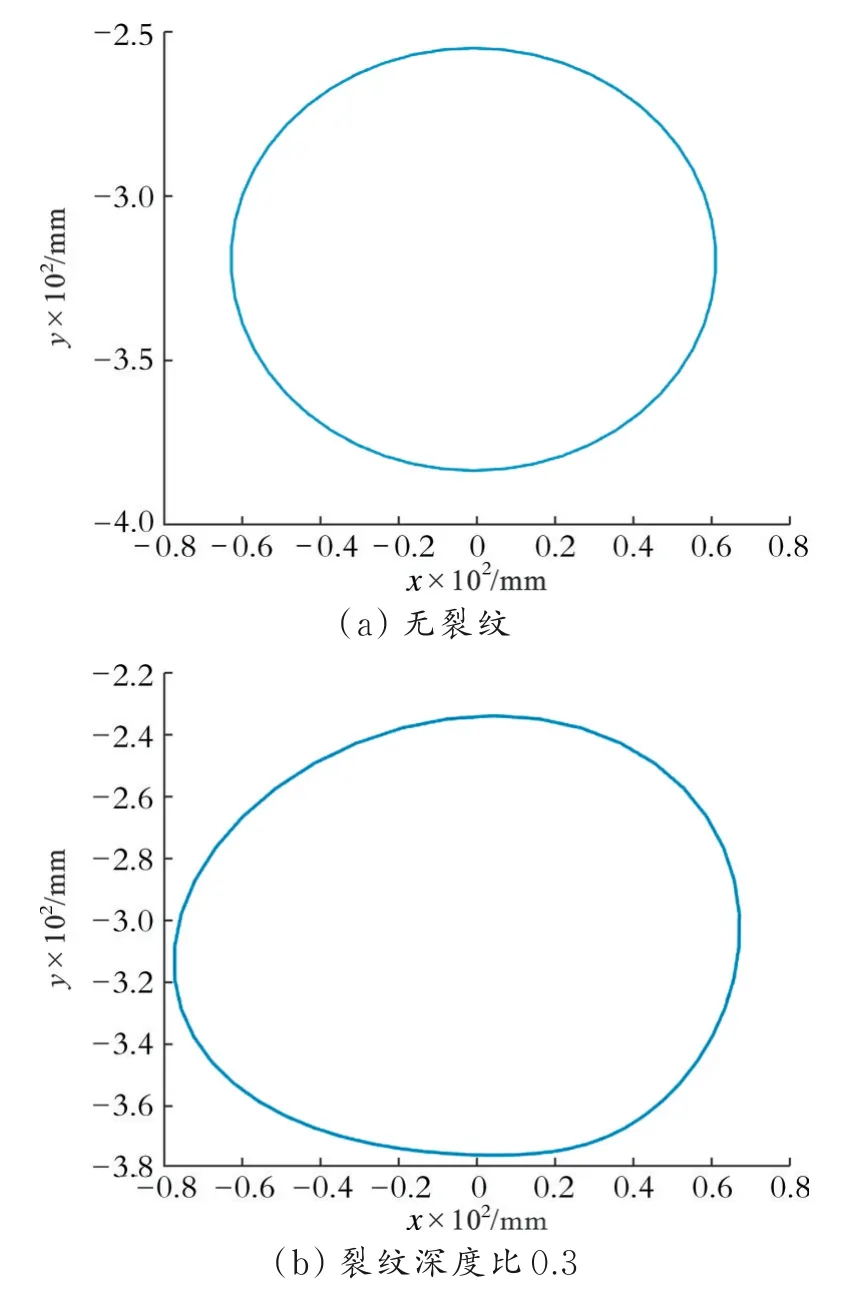
由图3—4可知，当裂纹较浅时，系统的时域波形比较平稳，振动分量以频为主，且轴心轨迹近似于一个椭圆形，与无裂纹时相似；随着裂纹慢慢加深，系统的振动幅值也随之变大；由于转轴上的裂纹在转动过程中不断地打开闭合，系统在一个旋转周期内出现多次振动，故频域图中出现了由裂纹引起的二倍工频振动分量，时域图中也出现了波形频率的叠加；随着裂纹深度比增加，轴心轨迹逐渐变得不稳定，出现了向内凹陷的现象；当裂纹深度比由0.7增加到1.0时，系统的更多高倍频被激发，振动幅值和二倍工频振动分量大幅度增加，轴心轨迹出现多个凹陷。这说明转子系统的不稳定性迅速增强，若裂纹继续扩展，系统会有失效的风险。

2.2 裂纹角度对转子系统振动的影响

针对振动响应最为强烈的裂纹深度比为1.0的裂纹转子系统，设置裂纹深度比为1.0，裂纹位于转轴正中间，设置转速为1 200 r/min，选取裂纹角度为30°、45°的斜裂纹，对裂纹角度不同的转子系统进行了仿真分析，其时域图及频域图（仿真结果）如图5所示，其轴心轨迹（仿真结果）如图6所示。

图5 裂纹角度不同的转子系统时域图及频域图（仿真结果）

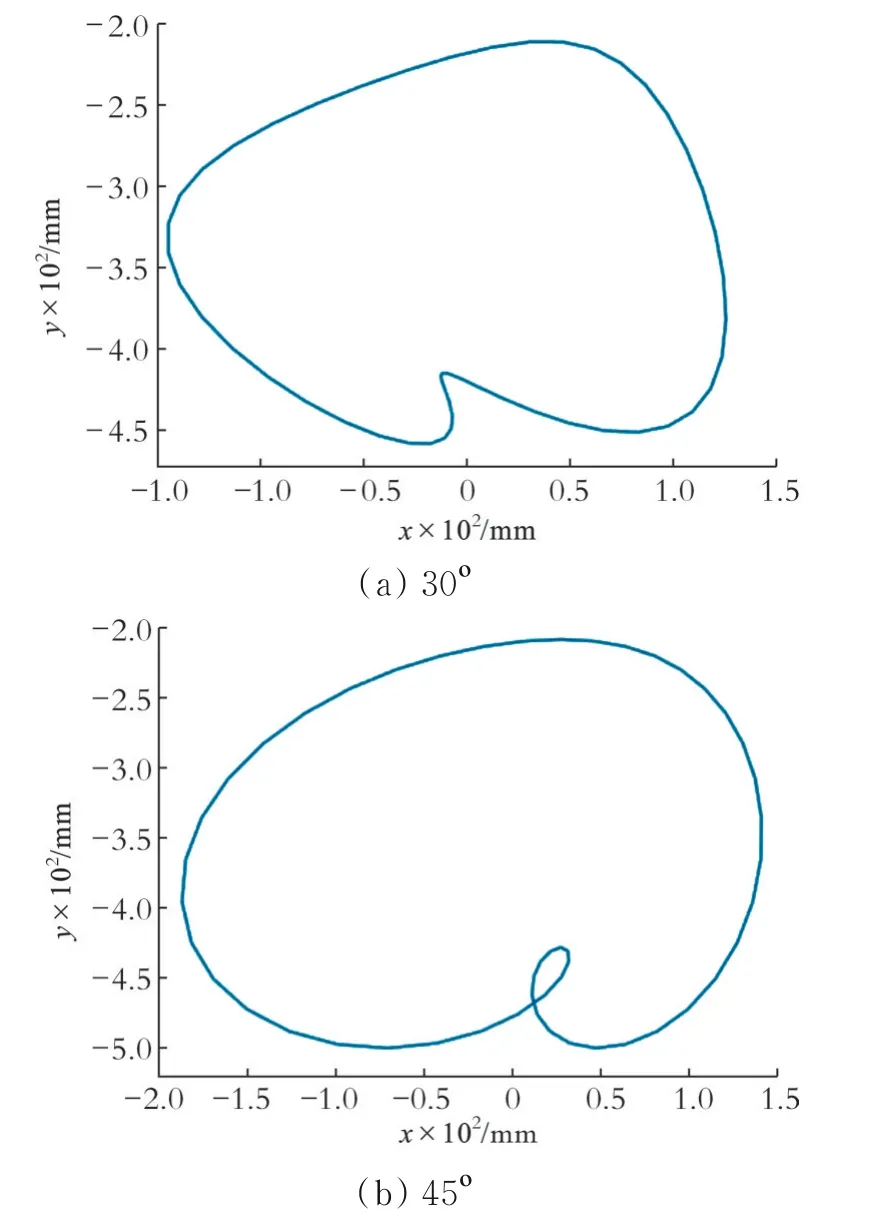
图6 裂纹不同角度的转子系统的轴心轨迹（仿真结果）

对比图5—6及图3—4中裂纹深度比为1.0的直裂纹转子系统数据可知，当裂纹深度和位置相同时，30°裂纹转子系统的振动幅值与直裂纹转子系统相比略有增加，轴心轨迹向内凹陷的程度进一步加深；当裂纹角度增加至45°时，其振动响应变得更为强烈，高倍频振动分量的幅值明显增加，且轴心轨迹继续向内凹陷以至出现套圈现象。由此可知，裂纹角度的增加会加剧裂纹转子系统的振动响应，裂纹角度为45°时变化尤为突出。对裂纹角度大于45°的情况，文献[12]进行了进一步探讨，结果发现裂纹角度为45°的转子系统响应最为剧烈，虽然裂纹角度大于45°时随着裂纹角度的增加系统振动响应缓慢减小，但减小幅度远低于裂纹角小于45°时的增加量。

2.3 转速对裂纹转子系统的影响

转速不同时转子重力与不平衡力之比不同，因此在不同转速下裂纹对系统的影响也不同。选取裂纹深度比为1.0且位于转轴正中间的直裂纹，裂纹深度、裂纹角度保持不变，分析了转速为1 800、3 000、4 200、5 400 r/min的系统时域、频域和轴心轨迹，总结了不同转速下的转子系统振动响应规律。不同转速下裂纹转子系统的时域图及频域图（仿真结果）如图7所示，其轴心轨迹（仿真结果）如图8所示。

图7 不同转速下裂纹转子系统的时域图及频域图（仿真结果）

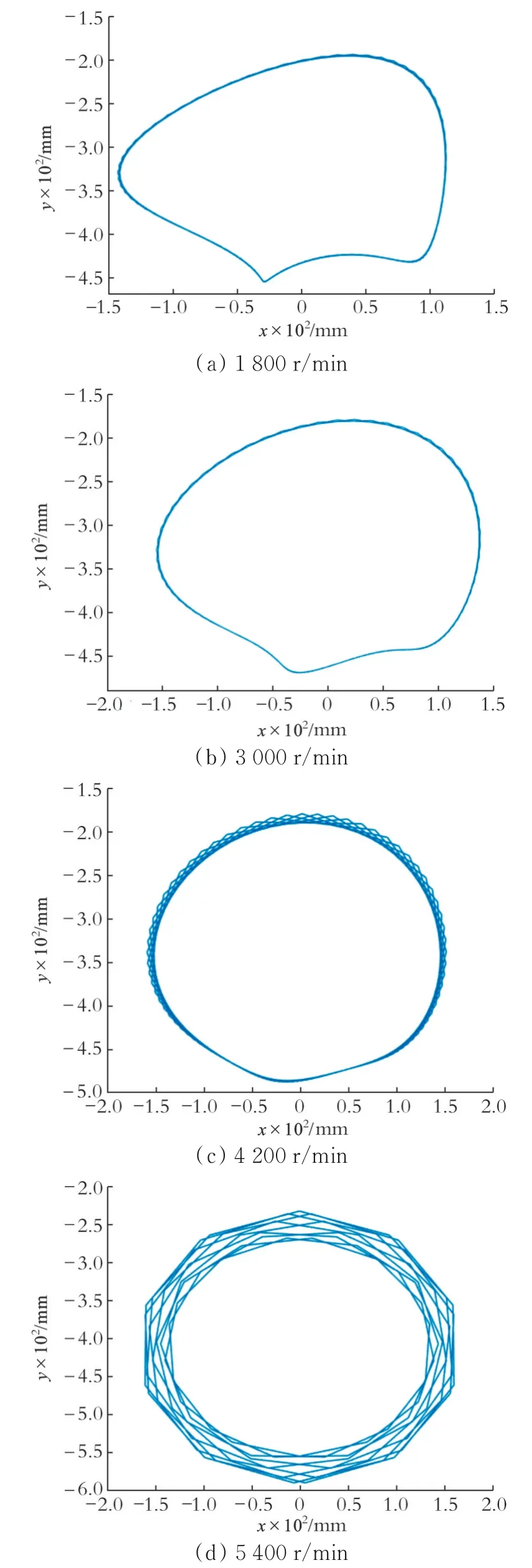
图8 不同转速下裂纹转子系统的轴心轨迹（仿真结果）

由图7—8可以看出，随着转速的增大，由偏心质量引起的工频逐渐增加，振动幅值随之变大；由裂纹引起的二阶、三阶倍频等高阶倍频增加量不明显，其效果被削弱，时域波形逐渐变得平稳，轴心轨迹由向内凹陷逐渐变得平滑，但出现了多个图形重叠的现象；当转速较大时，圆盘上的偏心质量是引起振动的主要原因，裂纹效果几乎消失，轴心轨迹由多个大小不一的椭圆形组成，具有一定规律性，复杂但不紊乱。这表明此时系统作拟周期运动，期间伴随着许多周期窗；如果转速继续增大，转子系统将以倍周期分岔进入混沌运动[16]。

3 裂纹转子系统的振动实验研究

在对裂纹转子系统的振动特性进行仿真分析的基础上，利用机械综合故障实验台，设计相应的实验方案，对裂纹转子系统进行振动响应实验。根据已有条件，搭建与上述模型相似的实验台，对不同裂纹角度和不同转速进行实验研究，测得其时间历程曲线和频域图形，并将实验结果与仿真数据进行比较，揭示裂纹转子系统的振动特性。

裂纹转子实验装置使用长兴昇阳科技设备有限公司提供的机械故障综合实验台（MCDS）。该实验台由电动机、伦茨SMV变频器、实验台基座、油路系统、分体轴承座以及卡环式轴承、卡环式转子、多种正常及故障转轴、联轴器、齿轮箱数据采集系统和传感器等实验零件组成。实验装置示意图如图9所示。

图9 实验装置示意图

3.1 直裂纹与斜裂纹转子系统振动实验分析

由于受实验条件的限制，选用位于转轴正中间的裂纹深度比为1.0的直裂纹与裂纹角度为45°的裂纹开展实验研究。分别将2根转轴安装在实验台上，检查并连接设备，设置转速为1 200 r/min。裂纹角度不同的转子系统时域图及频域图（实验结果）如图10所示。将实验数据保存并导入MATLAB软件中，得到了系统的轴心轨迹图（实验结果），结果如图11所示。由图10—11可知，直裂纹转子系统的振动特性较45°裂纹转子系统相对简单，其振动幅值较小，时间历程图更加光滑，轴心轨迹也相对平稳。与仿真数据对比，两者振动变化趋势大致相同，即45°裂纹转子系统振动更加复杂，图像变形程度较高。

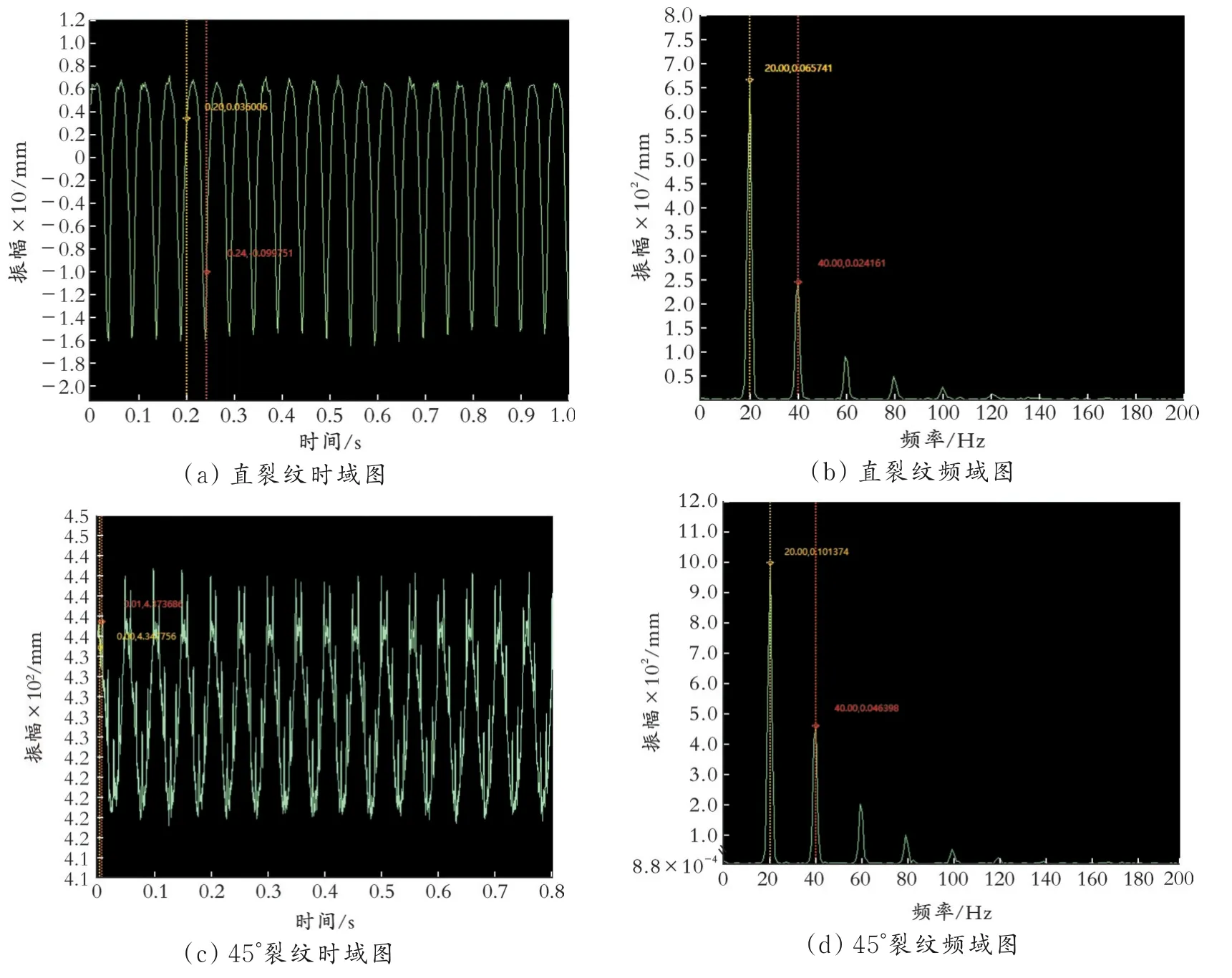
图10 裂纹角度不同的转子系统时域图及频域图（实验结果）

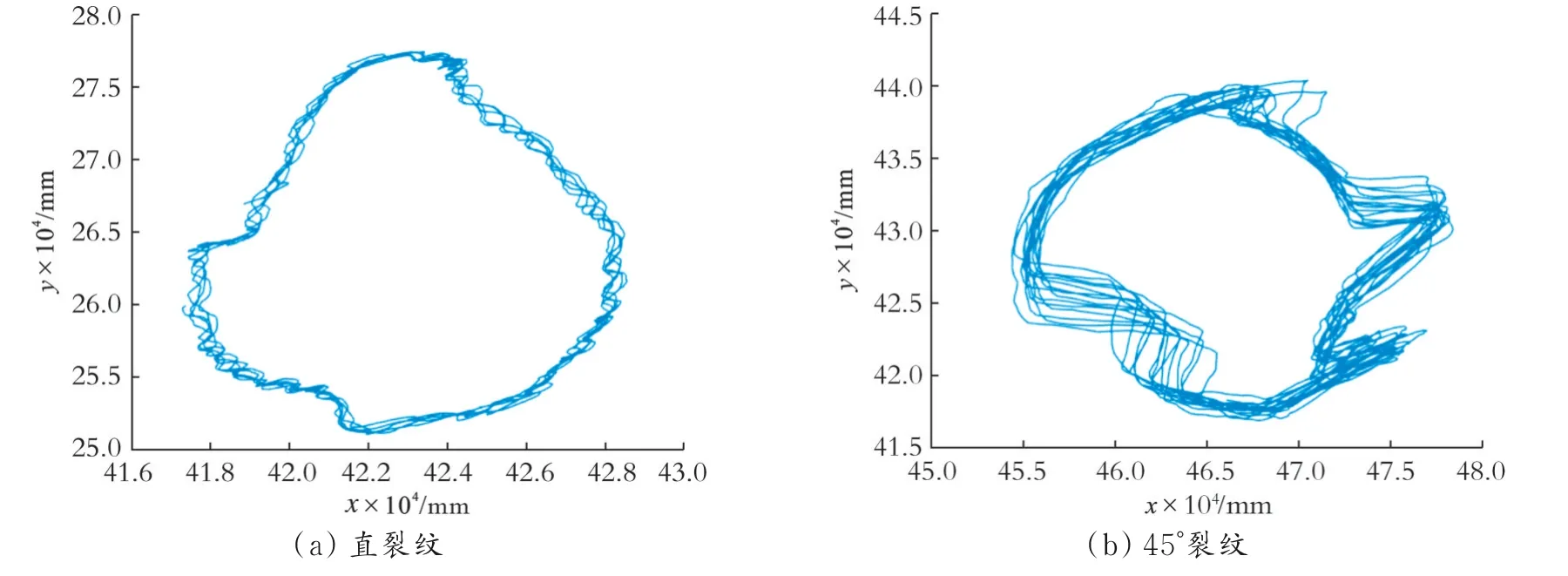
图11 裂纹角度不同的转子系统轴心轨迹（实验结果）

3.2 转速对裂纹转子系统的影响

为了实验台运行的安全，裂纹轴在运行时转速不宜过高。由于直裂纹转子系统振动特性较为简单，固选择直裂纹轴来研究不同转速下的转子系统振动特性。分别设置转速为1 650、1 500、1 200、1 125 r/min进行实验，结果如图12所示。由图12可以看出，随着转速的增加，时域波形趋于平滑，振动幅值增加，以工频分量最为明显，而由裂纹引起的高阶倍频分量效果被削弱；当转子系统在1 650 r/min和1 125 r/min转速下运转时，恰好处在该系统固有频率的1/2和1/3处，所以二阶和三阶倍频分量特别明显。与仿真结果相比，两者振动趋势几乎完全符合，验证了仿真结果及有限元模型的可靠性。

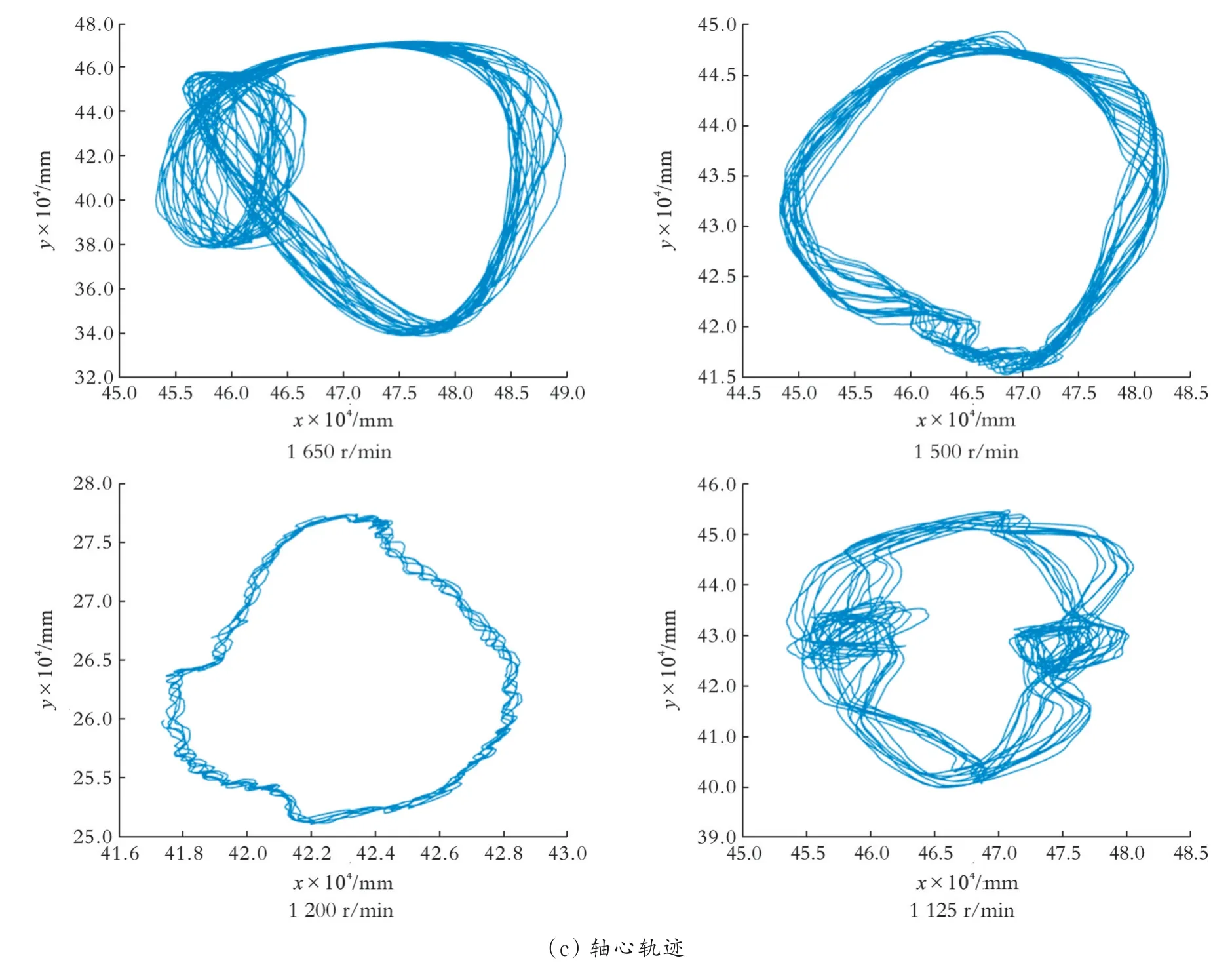
图12 不同转速下裂纹转子系统实验结果

4 结 论

（1）在裂纹较浅时，系统的振动特性与无裂纹转子系统相似。随着裂纹的加深，裂纹对转子系统的影响越来越大，时域图出现波形频率叠加现象，频域图出现由裂纹引起的高阶振动分量，轴心轨迹不再是光滑的椭圆，而是出现一个甚至多个向内的凹陷。此现象在裂纹深度比由0.7增至1.0时尤为明显。

（2）当转子裂纹角度变大时，系统受裂纹影响变大。30°裂纹转子系统与直裂纹转子系统振动特性相似；当裂纹角度增至45°时，系统的响应出现剧烈变化。随着裂纹角度变大，振动幅值明显升高，由裂纹引起的高阶振动分量也在变大，裂纹效果得到增强，轴心轨迹继续向内凹陷以至出现“套圈”现象。

（3）当转速发生变化时，系统的振动特性也发生改变。当转速较低时，裂纹对系统的影响较大；当转速为系统固有频率的1/3、1/2时，系统的3X、2X振动分量十分明显；随着转速的升高，系统受裂纹的影响越来越小，时域图逐渐变得光滑，轴心轨迹逐渐变成椭圆形，但出现了多个图形重叠的现象。若转速继续增大，转子系统将进入混沌运动。