基于小波变换‐海森伯格矩阵‐奇异值分解的图像水印算法

李文娜

（辽宁石油化工大学 人工智能与软件学院，辽宁 抚顺 113001）

互联网技术的快速发展改变了数字信息的传输与交流的方式，信息传播比以往更容易，但也容易导致严重的侵权问题[1‐3]。为此，需要更先进的技术和方法来保护数字信息版权。数字水印技术是数字信息版权保护的有效技术手段之一。图像水印的不可见性和算法鲁棒性是评估水印算法的主要指标。目前，数字水印技术在广播监控、所有者识别、所有权证明、交易跟踪、内容认证、拷贝控制和设备控制等领域得到了广泛应用[4]。

水印图像经常直接被嵌入到图像信号的空域中，直接修改像素值，但此类方法在图像信号被攻击时鲁棒性低，水印图像也可以嵌入到图像信号变换域中，例如离散余弦变换（DCT）[5]、离散傅里叶变换（DFT）、离散小波变换（DWT）和奇异值分解（SVD）等方法[6‐11]。为了提高嵌入方法的鲁棒性，相关人员研究了不同嵌入水印频域系数位置的方法。结果表明，人类视觉对信号的低中频系数更敏感。文献[10]首先将宿主图像从RGB空间转换到YCuCv空间，然后将Cv通道的数据进行小波变换，再将小波变换后的LL子带数据进行DCT变换，得到直流系数（DC）和交流系数（AC），最后将二值图像水印经过两次加密后的数据嵌入到DC系数。该方法嵌入水印图像为二值图像，嵌入尺寸为32×32，嵌入信息容量小，嵌入信息能力弱。文献[11]提出的算法不能很好地平衡嵌入水印图像的不可见性和算法的鲁棒性两个指标。小波变换的嵌入水印方法很难抵抗几何攻击，因此有学者提出了基于小波变换和奇异值分解的水印算法[6‐7]。

基于以上讨论，本文提出了基于小波变换‐海森伯格矩阵分解‐奇异值分解的可以抵抗多种攻击的彩色水印算法，算法在嵌入水印图像的不可见性和算法鲁棒性两个指标有很好的平衡。

1 基本理论

1.1 彩色空间变换

YCbCr彩色空间在视频系统、摄影系统和计算机系统中的应用很广泛，常见的图片格式JPEG、MPEG均采用此颜色表达格式。YCbCr彩色空间的Y、Cb和Cr分别代表亮度、蓝色色度和红色色度分量。由于人眼对Y分量更敏感，即使对Cb和Cr减少采样频率，人眼也不容易感觉到图像质量的变化，其优点是在一定程度上减少存储空间。从RGB彩色空间获得YCbCr彩色空间分量的表达式为[9]：

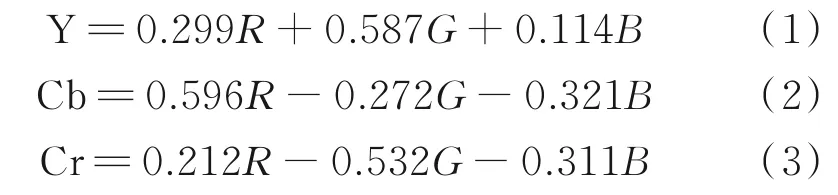
式中，R为RGB彩 色空间的红 色 分 量；G为RGB彩色空间的绿色分量；B为RGB彩色空间的蓝色分量。

1.2 小波变换

小波变换是一种常用的数学变换方法，在工程中应用广泛。二维图像信号小波变换是一维离散小波变换的推广，将信号在不同尺度上分解，从而得到原始信号的近似值和细节值。分解后包括LL、HL、LH和HH子带[6‐7]。LL子带是在行和列方向都通过低通小波滤波生成的系数，是图像的近似表示；HL子带是在行方向通过低通小波滤波后再在列方向上通过高通小波滤波生成的系数，表示图像的水平方向奇异特性；LH子带是在行方向通过高通小波滤波后再在列方向上通过低通小波滤波生成的系数，表示图像的垂直方向奇异特性；HH子带是由行和列方向通过高通小波滤波后生成的系数，表示图像的对角边缘特性。

图像的奇异特性通过低通小波滤波时保留，通过高通小波滤波时被滤除。小波变换后能量可以集中在少数系数上，因此可提高算法抵抗图像水印攻击的性能。

1.3 海森伯格矩阵分解

矩阵H的第一子对角线下元素都是0的矩阵被称为海森伯格(Hessenberg)矩阵。如果为对称矩阵，则它的海森伯格形式为对角三角阵。海森伯格矩阵分解用于方阵分解，其表达式为：

式中，X为n×n的矩阵；P为正交矩阵；H为矩阵X的海森伯格形式；HAD通常由豪斯霍尔德变换矩阵进行计算，豪斯霍尔德变换矩阵Q是一个正交矩阵，其表达式为：

式中，u为一个非零n维矢量；In为一个n×n的单位矩阵。在整个过程中，需要n−2步迭代运算其表达式见式（6）−（8）。

通过海森伯格矩阵分解后能够获得宿主图像更精确的成分，进而提高算法的鲁棒性。

1.4 奇异值分解

奇异值分解是另一种正交矩阵分解法，是最可靠的分解方法，分解后的三个矩阵分别为左奇异矩阵U、奇异矩阵S、右奇异矩阵V。其中，U和V代表两个正交矩阵UUT=In和VVT=In；S代表一个对角矩阵。假设K是一个对称矩阵，K的奇异值分解通过公式（9）计算[2]。

式中，U的列为KKT的标准正交特征向量；V的列为KTK的标准正交特征向量；S为一个包含U或V的按照降序排列的平方根的对角矩阵。

矩阵K的秩为r，如果满足r≤n，对角矩阵K中元素可以通过式(10)表示，矩阵K可以通过式(11)表示。

式中，ui、vi分别为U、V的第i个特征向量；σi为第i个奇异值。

1.5 Arnold变换

通过信息隐藏算法对秘密信息进行加密存在风险，如果黑客破解了水印算法可直接提取水印信息。Arnold变换也称为猫脸变换。对图像进行置乱，可以得到无序无内容无纹理的无意义的图像[11]。Arnold变换表达式为：

式中，（xn，yn）为变换(逆变换)前灰度图像像素的位置；（xn+1，yn+1）为变换(逆变换)后图像像素位置；a、b分 别 为 参 数；n为 变 换 次 数；N为 图 像 的 长或宽。

当图像为正方形时，经过n次Arnold变换后的数据可以通过n次逆变换恢复。Arnold逆变换表达式为：

2 本文算法

本文提出的水印算法可以实现二值水印、灰度水印和彩色水印的嵌入和提取，宿主图像通过R级小波变换实现多尺度的水印嵌入和提取。

2.1 水印嵌入算法

水印嵌入算法的输入为宿主图像C和水印图像W，输出为嵌入水印的宿主图像C*。C、W和C*的尺寸分别为M×M×3、N×N×3（如果水印为二值图像和灰度图像，则其尺寸为N×N）和M×M×3。水印嵌入的具体步骤为：

步骤1读取宿主图像和水印图像。

步骤2将宿主图像从RGB彩色空间转换到YCbCr彩色空间。如果水印图像是彩色图像，同样将RGB彩色空间转换到YCbCr彩色空间。水印图像如果是二值或灰度图像，则省略此步。

步骤3对宿主图像的Y、Cb、Cr分量进行R级小波变换，获得各分量的LL、LH、HL和HH系数。

步骤4对各LL子带系数进行海森伯格矩阵分解获得海森伯格矩阵H。

步骤5对海森伯格矩阵H通过式（9）进行奇异值分解，获得S、U和V。

步骤6对水印图像的各个分量进行Arnold变换，将水印图像置乱，消除像素的空间相关性，使算法抗攻击能力增强。同时，将(a,b,n)作为水印算法的第一密钥。

步骤7对Arnold变换后的置乱图像进行奇异值分解，获得Uw、Sw和Vw分量。

步骤8Uw和Vw分量通过混沌系统的逻辑斯谛映射进行加密，加密后的分量分布标记为Uw1和Vw1。

步骤9在步骤5获得的S分量上，按式（14）嵌入步骤7获得的Sw矩阵分量。其中，α为嵌入系数，同时作为水印算法的第二密钥。如果水印是灰度或二值图像，水印分量嵌入位置选择宿主图像的Y分量对应的系数。

步骤10嵌入水印的子带H*通过逆奇异值分解合成，其表达式为：

步骤11新的低频子带系数通过逆海森伯格矩阵重构，其表达式为：

步骤12嵌入水印的各个图像分量通过逆R级小波变换获得。

步骤13嵌入水印的宿主图像从YCbCr彩色空间转换到RGB彩色空间，标记为宿主图像C*。

2.2 水印提取算法

在水印提取算法中，输入为含水印的宿主图像C*，输出为提取的水印图像W*。水印提取的具体步骤为：

步骤1将含水印的宿主图像C*从RGB彩色空间转换到YCbCr彩色空间。如果水印图像为彩色图像，同样将RGB彩色空间转换到YCbCr彩色空间。

步骤2含对水印的宿主图像的Y*、Cb*、Cr*分量进行R级小波变换，获得各分量的LL*、LH*、HL*和HH*系数。

步骤3对各分量的LL*子带系数进行海森伯格矩阵分解，得到含有水印的海森伯格矩阵。

步骤4对各分量的通过式（9）进行奇异值分解，得到

步骤5通过式（17）获得提取的水印奇异值分量Sw2。

步骤6Uw1和Vw1分量通过混沌系统解密，解密后的分量标记为Uw2和Vw2。

步骤7各彩色分量的Sw2、Uw2和Vw2通过逆奇异值分解操作后获得提取的YCbCr彩色空间的水印图像。

步骤8提取的YCbCr彩色空间的水印图像各彩色分量在第一密钥的参与下进行逆Arnold变换，得到YCbCr彩色空间的水印图像W2。

步骤9对W2进行从YCbCr彩色空间到RGB彩色空间的转换，获得提取的水印图像W*。

3 实验结果和分析

为了验证水印算法的有效性，进行了仿真实验。所使用的宿主图像为真彩图像，水印图像可以是彩色图像、灰度图像或二值图像，宿主图像和水印图像如图1所示。

图1 宿主图像和水印图像

其中，图（a）−（c）像素为512×512，图（d）−（f）像素为256×256，图（g）像素为128×128，图（h）像素为64×64，图（i）像素为32×32。如果嵌入水印为二值图像或灰度图像，则忽略水印嵌入算法中的步骤2。

3.1 水印的性能评价指标

为了确保嵌入水印信息的安全，嵌入水印的宿主图像应该为不可见，该指标通常由峰值信噪比和结构相似度来衡量。峰值信噪比的表达式为：

式中，MSE为宿主图像C和嵌入水印的宿主图像C*之间的均方误差分别为宿主图像和嵌入水印的宿主图像的具体位置（i,j）处的像素；Cmax为宿主图像中像素最大值。

结构相似度表达式为：

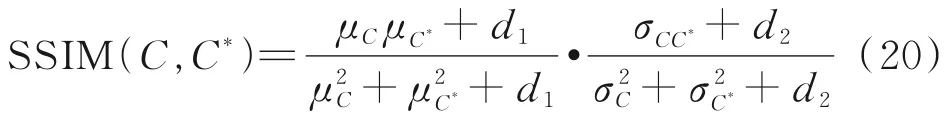
式中，μC、μC*分别为宿主图像C和嵌入水印的宿主图像C*的均值；分别为宿主图像C和嵌入水印的宿主图像C*的方差；σCC*为宿主图像C和嵌入水印的宿主图像C*的协方差；d1、d2分别为避免分母为零设置的两个变量，通常取接近零的很小的正数。

用归一化相关系数NC来衡量提取水印图像W*和嵌入水印图像W的鲁棒性。

式中，Wi,j、分别为嵌入水印图像和提取的水印图像具体位置（i,j）处的像素值。

计算所得NC值在0和1之间，其值越大说明提取的水印和原始水印的相似性越好。

3.2 不可见性和鲁棒性分析

实验中对不同尺度的水印图像及对彩色图像、灰度图像和二值图像的水印进行了嵌入和提取。嵌入的水印图像尺寸影响嵌入水印的宿主图像的可见性和提取算法的鲁棒性。选择宿主图像Lena像素为512×512，水印图像Flowers像素为256×256，不同嵌入比例因子下的归一化相关系数、峰值信噪比、结构相似度如图2−4所示。

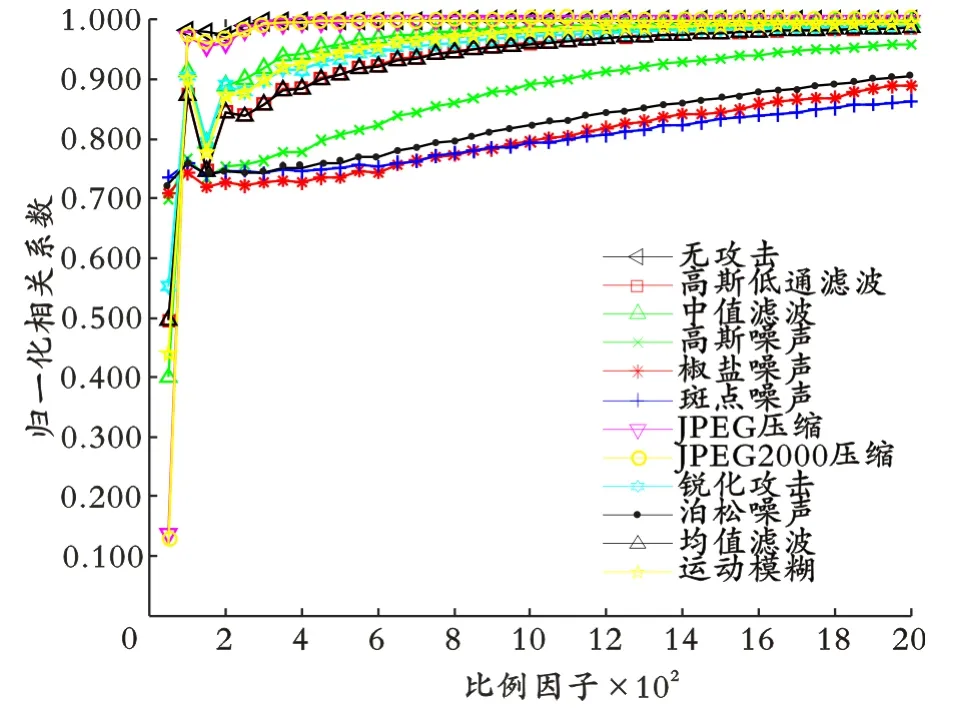
图2 不同嵌入比例因子下的归一化相关系数

图3 不同嵌入比例因子下的峰值信噪比

图4 不同嵌入比例因子下的结构相似度

不同尺寸的水印图像及不同嵌入比例因子的水印算法的PSNR、SSIM、NC性能指标如表1所示。

表1 不同尺寸的水印图像及不同嵌入比例因子的水印算法的PSNR、SSIM、NC性能指标

选择宿主图像Lena像素为512×512及水印图像Flowers像素为256×256进行了嵌入比例因子为0.08的多种攻击实验，对嵌入水印的图像进行多种攻击后进行了嵌入水印图像的提取。提高嵌入比例因子，以提高水印算法的鲁棒性。受到不同攻击时水印算法的PSNR、SSIM、NC性能如表2所示。

表2 受到不同攻击时水印算法的PSNR、SSIM、NC性能

3.3 相关算法比较

采用宿主图像像素为512×512的lena彩色图像、水印图像像素为32×32的二值图像进行实验，实验参数与文献[10]相同。本算法对灰度图像、彩色图像水印嵌入和提取时，需要较小的嵌入比例因子；对二值图像进行水印嵌入和提取时，需要较大的嵌入因子。实验中选择嵌入比例因子为10。宿主图像嵌入二值图像水印后，未受攻击时不同水印算法PSNR指标如表3所示。进行多种攻击后提取水印，受到多种类别攻击时不同算法的鲁棒性如表4所示。

表3 未受攻击时不同水印算法的PSNR dB

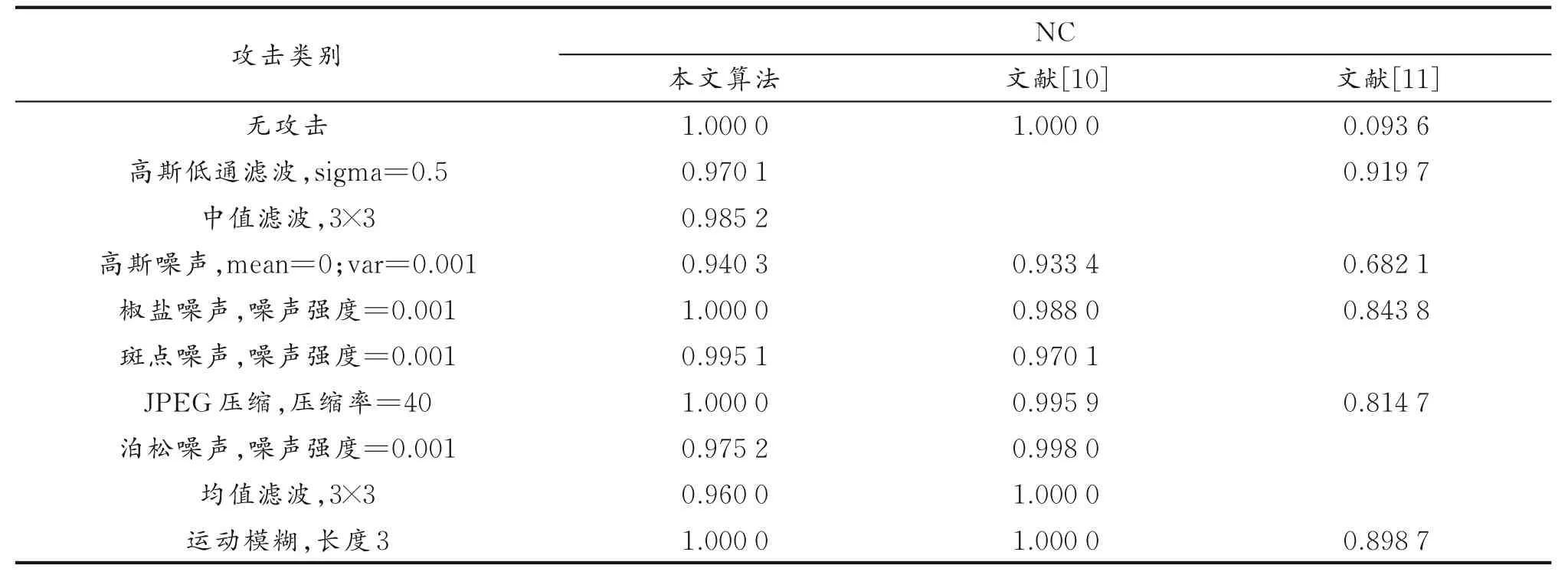
表4 受到多种类别攻击时不同算法鲁棒性指标

4 结 论

结合Arnold变换和混沌加密系统，提出了一种新的基于DWT‐HAD‐SVD的水印算法。仿真结果表明，嵌入水印的宿主图像有优质的不可见性；水印图像能清晰地从受到各种不同攻击的嵌入水印的宿主图像中提取出来。该算法适用于不同的水印尺寸，兼容彩色图像水印、灰度图像水印和二值图像水印，具有嵌入水印信息的容量大、抗攻击性强等优势，具有一定的应用价值。