基于相变松弛法则的水下爆炸空化模型研究

余 俊， 王海坤， 刘建湖， 汪 俊， 毛海斌， 周章涛

(中国船舶科学研究中心，无锡 214082)

1 引 言

空化作为水下爆炸过程中的一种重要现象，其对水中的冲击波传播、爆炸气泡运动以及结构物的冲击损伤都会产生重要影响。对于水下爆炸过程中空化现象的研究，早期可以追溯到Taylor[1]针对水下爆炸流固耦合过程提出的Taylor平板模型，对空化的产生机理进行了理论探索。此后，文献[2-5]基于各种假设对水下爆炸空化现象进行了理论分析与解释，并建立了部分经验公式。由于水下爆炸空化过程的复杂性，理论模型研究对象基本都是针对简单理想工况，其应用范围受到了较大的限制。在试验研究方面，文献[6-8]对近水面爆炸空化现象进行了记录与观察，为水下爆炸空化的机理研究提供了部分宝贵的试验数据。理论研究的局限性以及实验研究的不可预见性，使得水下爆炸空化的数值模拟研究显示出较大的优势。目前空化模型主要分为 one -fluid模型与 two -fluid模型两大类。one -fluid模型主要以cut-off模型[9]、isentropic模型[10]和Schmidt模型[11]等为典型代表，其主要思想是当液体中的压力小于饱和压力，认为就会出现空化，其中各种模型的具体差别体现在空化流场中压力或者密度计算的复杂度不同。two -fluid模型则主要以文献[12-15]提出的4-euqation和6-equation等模型为主，将可压缩流体控制方程与空化相变模型相结合，通过追踪空化质量分数的演化来捕捉空化的产生、发展与溃灭过程。Chiapolino等[12]提出了汽-液两相平衡态计算的简化方法，避免了繁杂的迭代计算过程，提出了空化相变计算效率。Zhang[19]将five-equation与相变模型结合来模拟空化。

受到认识水平以及计算方法的限制，目前水下爆炸空化计算领域使用的基本均是 one -fluid模型。与 one -fluid模型相比，two -fluid模型要复杂得多，需要充分考虑空化热力学运动过程中的质量与热量转换，对于计算的守恒性要求更严格。但是 two -fluid模型能够持续地追踪蒸汽相的演化过程，从逻辑上来说该方法更加科学合理。因此，本文拟采用4-equation模型来描述多相流运动，其中汽-液两相之间的相变过程引入松弛法则进行处理。在此基础上对上述模型进行了数值测试，最后将其应用到近水面爆炸空化研究领域。

2 计算模型

2.1 控制方程

对于水下爆炸运动等瞬态响应过程，可以忽略传热、粘性以及化学反应等影响，采用基于等压和等速度假设条件下的多相可压缩流体计算模型4-equation 来描述[12]：

(1)

控制方程中参数k表示混合流体中各相成分，为了计算模型表达简便，本文约定，k=1表示液相成分，k=2表示蒸汽相成分，k=3,…,N表示其他气相或液相成分，但其中的气相不会转换为其对应的液相，液相也不会转换为其对应的气相。统一令N=3，且k=3只表示气相，对于其他情况可以简单类推。

2.2 状态方程

为使系统(1)封闭，需要补充流体的状态方程。在流体计算模型中普遍采用的是刚性气体方程(SG)，能够描述多种液相或者气相流体的运动特性[16,17]。近年来NASG方程逐渐得到采纳，该方程修正了SG方程对液相介质中分子排斥力效应描述的不足[18]，可表示为

(2)

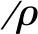
(3)

式中 下标sat表示饱和态，参数A,B,C,D和E分别为

(4)

式中Cp,k为k相流体定压比热容。液态水、水蒸汽以及空气的NASG状态方程参数列入表1，第4节算例涉及到水中空化问题所采用的计算参数均采用表1的参数[14]。

表1 液态水、水蒸气和空气的NASG方程参数 (国际单位)Tab.1 NASG coefficients for liquid water,vapor water and air

2.3 空化模型

控制方程(1)并未考虑各相之间发生的相变过程，是从纯物理几何运动的守恒角度来描述流体的守恒运动过程。对于流体中发生液相与其对应蒸汽相介质之间物质与能量转换的情况，可以参考化学反应过程中判断过程进行方向的判据，认为在达到平衡态之后液相与蒸汽相之间的吉布斯(Gibbs)自由能相等。同时结合控制方程(1)的假定，可以认为系统达到平衡态后满足关系式[19]为

(5)

将式(2,3)代入式(5)，可转换为

(6)

式中ppartial为气体混合物中蒸汽相的分压，由式(6)可知其与蒸汽相的摩尔质量分数成正比。非线性方程(6)可以采用迭代方法进行求解，如Newton-Raphson方法。

3 数值方法简介

控制方程(1)与状态方程(2,3)以及空化相变方程(6)共同构成了带有相变转换的多相可压缩流体系统方程组。该类计算模型的数值离散可以利用相变松弛法则进行分步求解[19]。第一步求解齐次双曲型方程组(1)，需要结合状态方程(2)，利用二阶MUSCL-Hancock方法以及HLLC近似黎曼求解器。通过该步获得中间步变量(υ,e,p,T,Yk)。第二步采用Newton-Raphson迭代方法求得相变转换平衡态时的状态量(p*,T*,Yk =1,2)。

(7)

式中 参数ξi和ξ定义如下。

(8)

图1 常温常压下气液两相混合流体声速随气体体积分数的变化Fig.1 Sound speed of gas-liquid two -phase mixture with gas volume fraction at room temperature and pressure

4 数值测试及算例

4.1 含气率较高的激波管问题测试

将整个流场中的蒸汽相初始质量分数设置为0.2，液相与气相的质量分数分别为0.1和0.7。计算域为[0,1 m]，均匀划分为400个网格。流场中密度和压力的初始间断面位置均为x=0.5 m，左右侧压力分别为2 bar和1 bar，两侧密度分别为1.94 kg/m3和1.02 kg/m3。图2为t=1 ms时刻密度、压力、速度、温度、液相与蒸汽相质量分数分布曲线，其中P -T和no P -T曲线分别表示有/无相变转换的计算工况，initial表示初始条件。从图2密度与压力分布可以看出，考虑相变转换后，两侧的冲击波与稀疏波波速均有所增加，温度与质量分数分布差异比较明显。可以发现向右侧传播的冲击波压缩低压流体后，流体中的蒸汽相质量分数有所增加，说明混合流体中的液相发生了相变，部分发生蒸发。同时向左侧传播的稀疏波使得左侧高压流体中水蒸气发生冷凝，液相质量分数有所增加。

图2 T=1 ms时刻流场密度、压力、速度、温度、液相与气相质量分数分布Fig.2 Distribution diagram of density,pressure,velocity,temperature,liquid phase and vapor phase mass fraction of flow field at T=1 ms

4.2 含气率极小的激波管问题测试

计算域、网格数、初始间断位置以及两侧初始压力同4.1节。左侧蒸汽相与空气的质量分数分别为9.45×10-8与10-5，右侧分别为1.92×10-7与10-5，两侧密度分别为1051.4 kg/m3与1046.5 kg/m3。图3为1.5 ms时刻各物理量的分布。可以看出，即使在水蒸气含量极低的条件下，计算模型也能对右侧冲击波传播过程中引起的蒸汽冷凝以及左侧稀疏波传播过程中引起液态蒸发等现象进行较好的捕捉。

4.3 双稀疏波问题测试

计算域、网格数、初始间断位置以及两侧初始压力同4.1节。初始流场中液相、蒸汽相和气相所占质量分数均为 0.0304， 0.5 和 0.4696，压力为 105Pa。初始间断位于x=0.5 m处，间断面左侧速度和右侧速度分别为-20 m/s和20 m/s。计算网格N=400，图4为t=0.5 ms时刻流场中密度、压力、速度、温度、液相和蒸汽相质量分数的分布。可以看出，在考虑了相变过程之后，流场的密度和压力等分布变化较大，主要还是由于其中的气相与液相之间发生了相变转换，两相质量分数都会产生变化，从而引起各物理量的重新分布。

图3 T=1.5 ms时刻流场密度、压力、速度、温度、液相与气相质量分数分布Fig.3 Distribution diagram of density,pressure,velocity,temperature,liquid phase and vapor phase mass fraction of flow field at T=1.5 ms

图4 T=0.5 ms时刻流场密度、压力、速度、温度、液相与气相质量分数分布Fig.4 Distribution diagram of density,pressure,velocity,temperature,liquid phase and vapor phase mass fraction of flow field at T=0.5 ms

4.4 近水面爆炸空化现象的模拟

采用二维轴对称模型研究近水面爆炸片空化现象。其中爆炸气体半径0.5 m，位于水下 3 m 位置，初始密度和压力分别为1343 kg/m3和4.29×108Pa，内部的水蒸气和气体质量分数分别为0.05和0.95。水面上方空气的初始密度和压力分别为1.3 kg/m3和105Pa，内部的水蒸气和气体的质量分数分别为0.001和0.999。水的初始密度和压力分别为1050 kg/m3和105Pa，内部的水蒸气和气体的质量分数分别为10-7和4.73×10-6。计算域取8 m×14 m,其中水深11m，空气厚度3 m，采用均匀网格，步长0.02 m。图5为t=1.5 ms， 3.2 ms 和4.6 ms时刻流场中密度、水蒸气质量分数、温度以及压力的分布。可以看出，从初始的冲击波传播到水面后反射稀疏波，到爆炸气体与水面之间出现低压区域，以及空化闭合等三个典型时刻。图5中每幅云图的观察窗口均为[-8,8]×[1.5,14] m2。

图6为纵向对称轴上距水面分别为0.2 m,0.4 m 和0.6 m处的水中压力时程曲线。可以看出，在2 ms～4 ms期间，空化处于产生与发展阶段，4 ms之后空化开始受到压缩，逐渐溃灭，最大溃灭压力达到7.6 MPa，约为冲击波峰值压力的15%。另外空化溃灭载荷的有效作用时间在1 ms～2 ms，是冲击波有效作用时间的2倍以上，可见其对结构的冲击效应不能忽略。

图5 T=1.5 ms，3.2 ms和4.6 ms时刻流场密度、蒸汽相质量分数、温度和压力云图Fig.5 Pseudo -color plots of the mixture density,vapor mass fraction,temperature and pressure at different times T =1.5 ms,3.2 ms and 4.6 ms

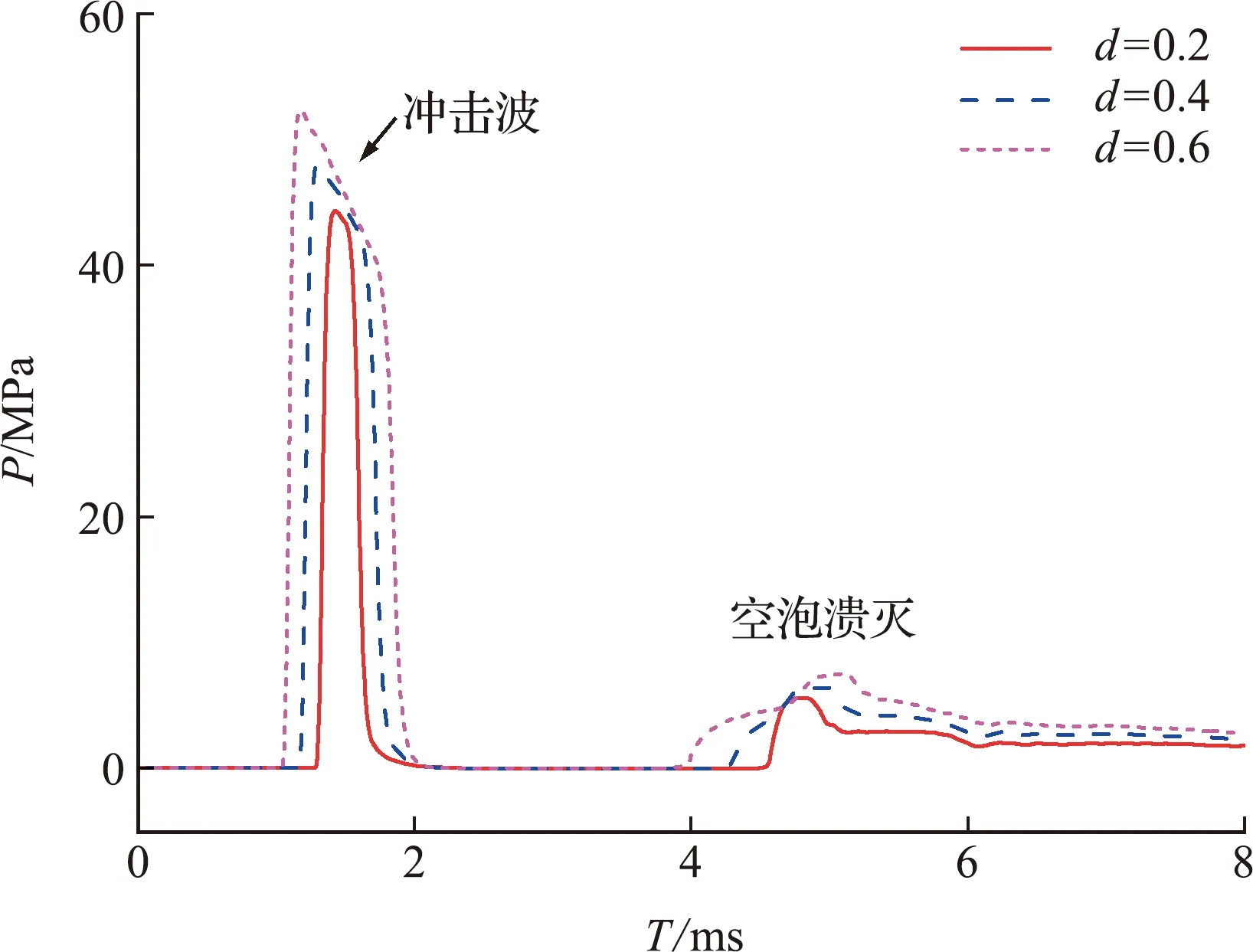
图6 对称轴上距水面不同间距处的压力时程曲线Fig.6 Pressure time -history curves for different vertical distance from the initial water surface on the axisymmetric axis

5 结 论

为了捕捉水下近水面爆炸过程中的空化现象，本文在多相可压缩流体模型基础上，考虑汽-液两相流体亚平衡状态下质量与热量交换过程中的热力学-化学平衡机制，实现了对空化相变的自动捕捉。控制方程采用分步法求解，首先利用 MUSCL-Hancock与HLLC黎曼求解器求解齐次双曲型方程，然后再利用迭代方法求解相变松弛方程。对该计算模型进行了多种工况下的空化相变测试，对于汽-液两相之间的蒸发与冷凝等相变过程具有较好的捕捉能力。最后将该模型应用于水下近水面爆炸空化现象的模拟，展示了水下爆炸空化的整个过程，捕捉了完整的空化闭合压力，本文计算方法与研究结果对提高水下爆炸空化机理的认识及其深入研究具有借鉴和指导价值。