草鱼幼鱼周身压力与曲率相关性数值模拟研究
杨国党, 胡 晓*, 石小涛, 余英俊, 张 奔, 龙泽宇
(1.三峡大学 水利与环境学院,宜昌 443000; 2.武汉大学 水利水电学院,武汉 430072)
1 引 言
自然界中鱼类具有较高的机动性,与人造机器鱼相比,其具有较高的推进效率。鱼可以在三维空间中自由游泳,灵活躲避捕食者或者搜寻猎物。对鱼类运动学的量化是分析鱼类运动力学的基础。
鱼在水中游泳复杂多样,不同水环境中呈现不同游泳姿态。为捕捉鱼的运动,通常以高速录像的形式获取鱼游泳行为,从中提取其运动学变量[1]。为了量化鱼在生育发展各个阶段的变化,Fontaine等[2]开发了一个视觉跟踪系统来估计鱼的姿势。柯森繁等[3]基于Matlab软件开发了一种跟踪鱼类中线的程序来获取鲢鱼的摆尾频率、加速度和速度等运动指标。为了进一步描述普遍鱼类运动学规律,Liu等[4]将鱼体的波动用波状函数描述,后续有很多学者对鱼波动方程进行了改进优化。
为了实现有效的运动控制,鱼类能够实现身体变形,且由此产生的速度和生物力学相联系,从而实现其高效游泳。鱼在结构复杂的栖息地游泳需要较高的机动性,包括其方向的改变程度和完成动作所需的空间[5]。有研究发现,较小的鱼具有较高的机动性,这主要得益于较小的鱼具有较高的弯曲程度[6]。沈昊嫣等[7]探究了鱼体曲率波的传播速度,发现主动弯矩的驱动频率高于鱼体结构基频时,曲率波的波速小于驱动波的波速。有研究提到,力学可以深化对鱼体形态变化和运动方式之间的理解[8]。王仲威等[9]基于曲率模型发现斑马鱼在弯曲阶段存在较大的正向力矩,而回摆阶段存在比较小的反向力矩。Thandiackal等[10]研究发现斑马鱼在转弯的早期阶段,弯曲接近最大曲率时,鱼体尾部区域压力作负机械功。由此可见,鱼类游泳姿态和力学机制对于解析鱼类行为十分重要。
综上所述,国内外很多学者对鱼类的行为学及动力学有所研究,但很少对鱼自由游泳时曲率和周身压力进行量化研究。因此本文以草鱼幼鱼为研究对象,基于实验拟合振幅曲线并验证拟合结果,量化了鱼体中线曲率和轮廓曲率的变化,分析了周期内曲率和压力的变化趋势和相关关系。本文可增加对鲹科鱼类自游泳弯曲状态和力学机制的认识并提供参考资料。
2 实验设计与方法
2.1 实验对象选取
为了获取真实鱼的运动学参数,以草鱼幼鱼为研究对象。实验对象购置于湖北省宜昌市某水产市场,选取体质活力较好的20尾进行实验研究。体长平均长5.2 cm±0.2 cm。实验前将实验对象放置于圆形玻璃水缸中暂养,水温保持在18 ℃±2 ℃,实验前24 h禁止喂食,全天不间断向鱼缸中充氧以保证溶解氧不小于6 mg/L。
2.2 实验装置与方法
实验装置如图1所示,在透明玻璃水槽中进行。该玻璃水槽的实际尺寸为长×宽×高=34.5 cm×20 cm×22 cm。实验前在玻璃水槽上方平行架设高速摄像机。水槽右侧架设激光拍摄系统,激光笔采用诺青激光笔(型号为NQ-506,波长为532 nm,功率为100 mW),棱镜为D形柱。图像处理系统选用笔记本电脑。示踪粒子密度为1.02 g/cm3,直径为20 μm~30 μm[11]。
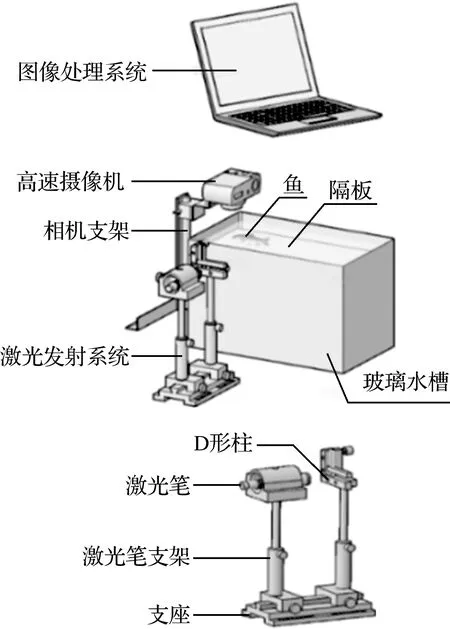
图1 实验装置Fig.1 Experimental device
2.3 视场获取方法
实验在无外界干扰的环境中进行。实验前在水槽中均匀撒入示踪粒子。实验时激光束通过D形棱镜形成约为2 mm厚的片光源,通过调节支架高度使片光源能够照射在鱼体侧线上。实验前严禁打开激光笔,以免对鱼造成惊吓。另外为了能够较好地看到鱼的侧线变化情况,在玻璃水箱一定高度架设隔板,防止草鱼幼鱼在空间上做俯仰运动,另外为防止激光反射形成亮斑,在水槽侧壁粘贴不透明胶带,减少干扰。高速摄像机空间分辨率为640×480(pixels2),每个视场拍摄5 min。
2.4 基于速度场的压力场重构基本方法原理
采用直接积分进行压力重构,基于二维不可压缩Navier-Stokes方程对压力梯度项进行积分。
不可压缩N-S方程为
(1)
两点之间压力差按式(1)确定。如x1和x2两点之间压力差为
(2)

又因为流体连续性方程为
(3)
式中xi为坐标,ui为xi方向上的速度(i=1,2,3,分别为x,y和z方向)。
由式(3)可知,压强梯度为粘性项和物质加速度之和,其中物质加速度欧拉表达式为
(4)
粘性项的速度场节点采用中心差分格式,表达式为
(5)
(6)
可以通过实测得到上述方程右侧节点处的速度,并结合式(3)通过两点之间的积分算出压力值。在积分时,测量误差是x1~x2路径累积,当前通过沿8条路径积分取其平均值,可大幅减小积分误差,以实现准确的对压力估算[12]。8条积分路径如图2所示,每条起源于域边界,分别从左上角(LU)、上(U)、右上角(RU)、左(L)、右(R)、左下角(LD)、下(D)和右下角(RD)向每个方向传播,平均各路径后则为点z的压强值。
(pL+ΔpL)+(pLU+ΔpLU)+(pLD+ΔpLD)+
(pRU+ΔpRU)+(pRD+ΔpRD)]
(7)

图2 积分路径Fig.2 Integral path
2.5 试验图像处理方法
采用互相关软件PIVlab 2.02处理速度场,利用标准FFT相关算法,查询区窗口大小为64×32(pixels2)。在2D视场下速度场分析之前对鱼可视轮廓遮罩,后续运用基于Matlab的运行程序QUEEN2计算压力场。为了便于后面模拟仿真,忽略胸鳍和简化了尾鳍,对鱼体主要轮廓进行分析。为了得到精细的鱼体周身流场信息,参考文献[13]研究理论,将幼鱼鱼体划分为头部、中部和尾部,具体定义为鱼吻到胸鳍之间的区域为头部(0~1/5BL);胸鳍与腹鳍之间区域为中部(1/5~3/5BL);腹鳍到尾柄区域为尾部(3/5~1BL),如图3所示。

图3 鱼体划分Fig.3 Fish division
2.6 运动学分析
2.6.1 鱼体波动振幅
鱼类游泳具有较高的机动性和灵活性,部分学者将鱼类的游动分为月牙尾推进、鳗鲡模式和鲹科模式[14]。草鱼幼鱼波动主要集中在后半部分,为鲹科模式。为了便于分析运动,此处定义草鱼幼鱼摆尾向前波动的过程中,当鱼尾向右摆动最大幅度时再摆动一个来回,这个过程历时为一个周期T。最终选择鱼体长BL=0.052 m的草鱼幼鱼近似直线游泳的视频,将其逐帧分解并参考文献[7,15]的理论方法提取鱼体中线,并建立坐标系,如图4(a)所示。

图4 相对体长下鱼体波动振幅曲线拟合Fig.4 Fitting of fish wave amplitude curve under relative body length
为便于分析草鱼幼鱼行为特征,对鱼的体长采用无因次化处理。利用式a(x/BL)=a0+a1(x/BL)+a2(x/BL)2+a3(x/BL)3进行二次和三次拟合振幅曲线,如图4(b)所示,拟合振幅曲线系数列入表1。

表1 振幅曲线拟合系数Tab.1 Amplitude curve fitting coefficients
2.6.2 鱼的波动行进方程
有关研究表明,通过对鱼类的二维研究,即使体型不同的鱼类,如鳗鱼、鳟鱼、鲭鱼和金枪鱼等,也显示出极其相似稳定的波动运动[16]。鲹科模式鱼类具有统一的运动学方程,为了形象地表示鱼的运动行为,将振幅a(x/BL)、波长λ、频率f和横向位移y(t,x/BL)组合成参数化的数学方程。鱼的运动方程可以描述为[17]
y=y0+a(x/BL)sin [2π(x/λ)-ft]
(8)
为了说明后续模拟的可操作性,利用Matlab软件绘制相对体长下鱼的包络线,如图5所示。图5 的包络线与图4提取结果具有可比性,鱼体头部横向位移幅度相对于尾部较小,鱼的尾部具有较高的灵活性。从运动学的角度来看本文研究结果实现了将运动学以参数化方程来描述,这为后面的模拟仿真提供了可行性基础。

图5 相对体长下鱼体包络线Fig.5 Envelope diagram of fish relative to body length
2.7 计算方法
2.7.1 数值计算
使用带有可控运动程序的水翼来复制柔性鳍或鱼体是研究鱼类运动学和推进力的有力工具[18,19]。为了便于仿真,本文以NACA0012作为鱼的二维简化模型,按实际鱼等比例缩放建立物理模型。对整个计算流体域进行网格离散划分,对鱼体游泳区域进行网格加密,单元总数为128684,网格模型如图6所示。进口采用速度进口(ν=0),出口设置为压力出口。速度-压力耦合采用SIMPLE算法进行修正。为了达到较高的收敛性,时间步长取0.0005 s。鉴于数值方法在文献[20]已有介绍,此处不再详细阐述。

图6 网格Fig.6 Grid
2.7.2 波动曲率
曲率是一种鱼体内部一致的测量,不需要完整的身体几何标志,表现了鱼在游泳过程中整个身体弯曲程度的度量[21]。曲率可表示为
(9)
2.7.3 鱼周身压力计算
鱼摆尾游动时与流体相互作用产生压力场。本文聚焦分析一个摆尾周期中线、体表曲率和鱼周身压力的相互关系。流体作用在鱼体上的压力可以表示为[22]
(10)
式中n为法向量,垂直体表指向外方向,p为压强值,A为轮廓长度上单位厚度的面积。
3 结果与分析
3.1 模型验证
为了进一步说明模拟结果的准确性和分析的可行性,选取t=0.65 s以及t=1.3 s时的游泳姿态,利用Tecplot与Origin对鱼体周身的压力分布进行分析,如图7所示。结果显示三次拟合振幅曲线比二次拟合振幅曲线能够更好地控制幼鱼摆尾行为,同时鱼体的周身流体压力与实测值的吻合度更高,因此,本文采用三次拟合的振幅曲线来模拟幼鱼鱼体的包络线运动规律,在此基础上对模拟结果进行分析。

图7 鱼周身实验值与仿真模拟压力值对比Fig.7 Comparison of experimental value and simulated pressure value of fish body
3.2 鱼体波动曲率变化规律分析
3.2.1 不同游泳姿态下鱼体中线曲率分析
图8为鱼游泳行进中线曲率变化分布。初始时刻,曲率最大处约在鱼体尾部前端,对应时刻曲率最大值为kmax=29 m-1,如图8(a)所示。从图8(b~d)可以看出,对应时刻曲率的最大值由尾部前端向后端发展。当t/T=1/2时,鱼的曲率最大处由尾部后端又逐渐发展到尾部前端。t/T=5/8~1是鱼回摆阶段,对应时刻kmax变化与之前相似,如图8(f~h)所示。这表明在一个周期内,草鱼幼鱼中线的kmax主要限于尾部前端和尾部后端之间往复变化。曲率最小值无明显变化规律。
总体上,在t/T=1/2之前,鱼自由前进过程中对应时刻最大曲率kmax呈先增大后减小变化趋势;在t/T=1/2之后,对应时刻曲率最大值与之前变化相同,方向相反。这在一定程度上说明鱼尾在摆动过程中草鱼幼鱼后半部分并非是向后伸展变化,而是向前有一定的弯曲。总体而言,对应时刻kmax分别在t/T=0,t/T=1/2和t/T=1时相对达到最小,而在t/T=1/4和t/T=3/4时达到相对总体最大值。当t/T=1/4~3/4,对应时刻kmax呈现先减小后增大的原因是鱼正处于S型摆尾阶段[23],中线弯曲最大处主要集中在鱼体后部。整个周期中对应时刻曲率最大值相对总体最大值和最小值分别为102 m-1和29 m-1。
有研究提到鱼体曲率与角度变化有关,但是很少提到鱼体变形与力学关联机制[24]。为了说明鱼体变形影响机制,本文将鱼体按体长划分为 10段。图9为每段中间点最大曲率在周期内的变化趋势,鱼体弯曲最大处主要集中在鱼体尾部,这为3.3节压力分析奠定基础。
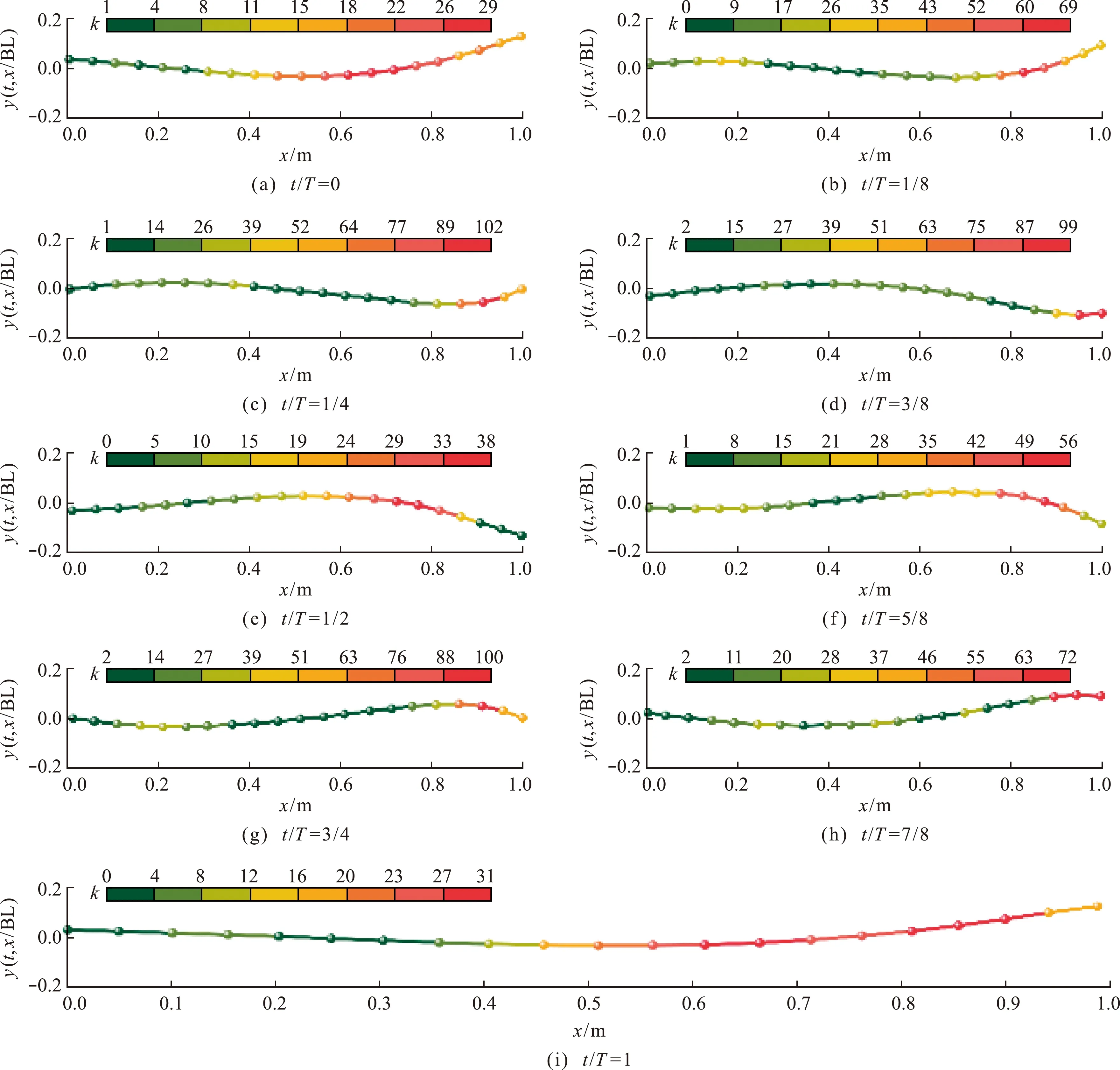
图8 不同时刻鱼体中线曲率变化Fig.8 Curvature changes of fish body at different times
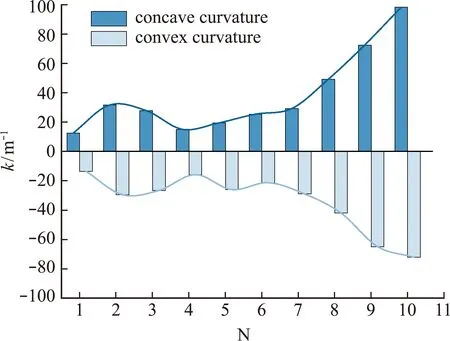
图9 周期内鱼体每段中线曲率峰值Fig.9 Peak curvature of each central line of the fish body in a period
3.2.2 中线曲率与周身曲率耦合
鱼头部分较硬,可视作刚体,鱼身部分富有弹性,可视作弹性体[25]。因为鱼体头部中线曲率和对应体表曲率的不一致性,本文只分析如图10所示鱼体中部和尾部对应中线曲率与周身曲率的关系。在t/T=1/8~1/2时,分析发现除鱼头部分外,不同游泳姿态下鱼体中线的曲率和幼鱼周身曲率均符合K=ak+b线性函数关系(k为中线曲率,K为周身轮廓曲率,P<0.05)。
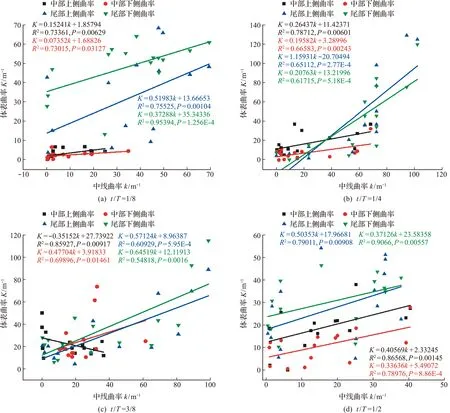
图10 幼鱼中部和尾部的中线曲率与体表轮廓曲率关系Fig.10 Young fish line at the end of the central,curvature relationship with surface contour curvature
3.3 幼鱼周身流体压力
3.3.1 鱼周身压力分布
图11为幼鱼周身的流体压力云图。如图11(a)所示,初始时刻鱼头周围流体表现为负压,鱼尾下侧表现正压,上侧表现负压,此时合压力变化范围为-9.6 Pa/BL~0 Pa/BL。之后鱼头向下侧轻微摆动,表现为下侧流场为正压,上侧表现负压且有增大趋势,如图11(b)所示。t/T=1/4时,如 图11(c)所示,鱼体头部有大面积高压力区出现,这是由鱼头向下摆动速度诱导的,此刻鱼尾压差变化区间为-1.9 Pa/BL~0 Pa/BL。之后在惯性力作用下鱼尾继续向下摆动,显而易见在t/T=3/8时鱼尾表面流体压力发生变化,鱼尾下侧的流体压力高于右侧。当t/T=1/2时,在幼鱼自身行为主导驱动下,鱼体下侧的摆尾幅度达到极限,如图11(e)所示。t/T=5/8~1时,鱼尾开始回摆,整个压力场变化与前半个周期相反,如图11(f~i)所示。

图11 鱼周身压力变化云图Fig.11 Cloud chart of pressure changes around fish
值得注意的是,在t/T=1/4和t/T=3/4时刻,约在鱼体尾部流体表现为正负压交替现象,主要原因是各部位的摆动速度和弯曲程度不同所致。
3.3.2 鱼体分段曲率和压力变化分析
为了探寻鱼体每段中线曲率与对应鱼体表面的流体压力关系,拟合每一段中线曲率和鱼周身流体压力,如图12所示。从图12(a~b)可以看出,鱼体头部每段中线曲率与下侧表面流体压力变化趋势基本一致;相应地在鱼体尾部,每段中线曲率主要与鱼体上侧表面流体压力随时间变化趋势一致(图12(g~i));然而在鱼体中部约(1/2~3/5)BL区间段,中线曲率和鱼体上下表面流体压力均未随时间呈现一致的变化趋势(图12(f))。此外,鱼体表面流体压力与曲率在周期内均出现交叉变化,曲率波峰最大滞后压力波峰约为3/8T。结合图9可知,每段中线曲率最大值变幅越大,周期内相位滞后随鱼体长度的变化就越明显,这与曲率波滞后机电信号类似[26]。

图12 周期内分段曲率和压力随时间变化曲线Fig.12 Curve of piecewise curvature and pressure over time in a period
3.3.3 鱼周身压力-曲率耦合
图13显示了鱼体中部和尾部的表面流体压力与曲率的关系。由于t/T=5/8~1是鱼回摆过程,因此只选择t/T=1/8~1/2区间作为展示。从图13(a)可以看出,鱼体中部流体压力主要随曲率增大而增大(P<0.05)。随着鱼体向前游动,鱼体中部和尾部的上下侧流体压力均随曲率的增大而增大(P<0.05),如图13(b)所示。当t/T=3/8时,鱼体中部下侧流体压力和曲率呈正相关关系,而上侧流体压力与曲率呈负相关变化关系,如 图13(c)所示;鱼体尾部上下侧流体压力和曲率均呈正相关关系(P<0.05)。当鱼体向下摆尾最大限度时,鱼体中部两侧表面压力和曲率呈负相关关系,鱼体尾部表面流体压力和曲率表现为负相关关系(P<0.05),如图13(d)所示。
从图13可以看出,鱼体中部和尾部两侧表面流体压力和曲率大多表现出明显的线性关系(K=aF+b)。结合图11可知,流体与鱼体相互作用时,鱼对流体的压力像波一样向四周扩散,并逐渐减弱,所以鱼对流体压力并非持续性增大,又因为曲率最大处并非是压力最大处,所以会出现曲率和压力呈负相关变化。另外由于鱼逐渐摆尾向下游动,鱼体中部和尾部之间出现负压和正压逐渐过渡,这也是曲率较大处呈现压力先减小后增大(或先增大后减小)的原因。此外,由于幼鱼中间区域和尾部中线曲率与表面流体压力有较明显的线性关系(P<0.05),也说明鱼体中部和尾部整体表面流体压力与中线曲率也呈线性关系。
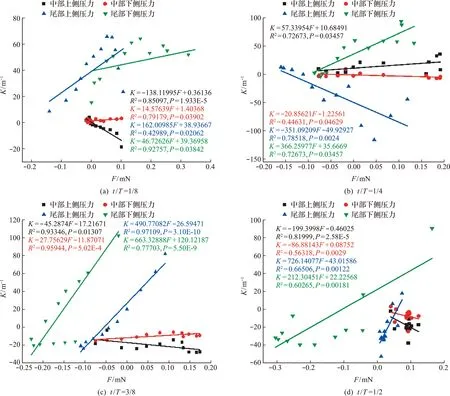
图13 鱼体中部和尾部周身流体压力与鱼体曲率的关系Fig.13 Correlation between pressure and curvature in the middle and tail of fish
4 结 论
本文利用仿真模拟的方法分析了草鱼幼鱼的自由摆尾行为,量化了鱼体中线曲率在一个摆尾周期内的变化,同时对幼鱼周身流体压力与鱼体表面和中线曲率的相关性进行了分析,探究了幼鱼中部和尾部的周身流体压力和曲率的变化规律,主要结论如下。
(1) 拟合三次振幅曲线方程比传统二次振幅曲线方程能够更好控制幼鱼的自由摆动,且得到的鱼体周身流体压力与PIV实测结果吻合度更高,相比常用的二次模拟结果要更精确。
(2) 幼鱼中部和尾部的中线曲率与体表曲率呈较为明显的线性关系(P<0.05),且鱼体中线最大曲率的变化主要局限于幼鱼尾部。
(3) 幼鱼尾部和头部的中线曲率分别与鱼体上下侧的流体压力变化趋势一致;而在幼鱼的中间部位,鱼体的中线曲率与流体压力未有一致走势,曲率波峰滞后压力波峰最大可达3/8T。
(4) 幼鱼中部和尾部的周身流体压力在前半个运动周期内和鱼体体表、中线的曲率均呈线性相关。
本文限制了幼鱼垂向运动,通过实验获取幼鱼运动学参数和周身截面流场。利用实验数据拟合分析及标定数值模型,实验与模拟结果的比对说明本方法可较好地模拟鱼体曲率变化和周身压力的关系,对理解幼鱼自推进变形和受力机制具有一定的意义。

