高考中几种机械能图像的理解与认知

许 文

(华中科技大学附属中学)

机械能E包括动能Ek与重力(弹性)势能Ep.物体在运动过程中,动能与势能可能随时间和空间的变化发生变化,其变化规律可用函数关系式和图像两种方式表达.图像是反映变化关系的一种直观手段,是一种数与形相结合的思想.与机械能有关的图像一直倍受高考命题者的青睐,在近几年高考中频繁出现.本文通过典型实例解析几种机械能图像,帮助同学们理解机械能图像问题.

1 Ek-x 图像

Ek-x图像描述的是物体的动能Ek随位移x变化的关系.设物体受到的合力大小为F,在一段很短的位移Δx内物体动能的变化为ΔEk.由动能定理有FΔx＝ΔEk,可得.故Ek-x图像中直线或曲线某点切线的斜率的绝对值表示物体在运动方向上受到合力F的大小.

例1(2017年江苏卷)一小物块沿斜面向上滑动,然后滑回到原处.物块初动能为Ek0,与斜面间的动摩擦因数不变,则该过程中,物块的动能Ek与位移x关系的图线是( ).

解析设斜面倾角为θ,物块质量为m,物块与斜面间的动摩擦因数为μ,则物块在斜面上运动过程中受到的动摩擦力大小Ff＝μmgcosθ不变.物块沿斜面上滑过程中受到的合力大小F1＝mgsinθ＋Ff即为上滑过程中物块动能Ek随位移x的变化率,故描述物块上滑过程的Ek-x图像的斜率k1不变;物块沿斜面下滑过程中受到的合力大小F2＝mgsinθ－Ff即为下滑过程中物块动能Ek随位移x的变化率,故描述物块下滑过程的Ek-x图像的斜率k2不变,且k2的绝对值小于k1的绝对值,故选项C正确.

点评物体的动能随位移的变化率的绝对值表示物体受到的合力大小.正确分析物块沿斜面上滑和下滑过程中受到合力的大小及特点,并结合Ek-x图像变化率的物理意义,进而对Ek-x图像的分布作出定性判断.

例2(2020 年江苏卷)如图1 所示,一小物块由静止开始沿斜面下滑,最后停在水平地面上.斜面和地面平滑连接,且物块与斜面、物块与地面间的动摩擦因数均为常数.该过程中,物块动能Ek与水平位移x关系的图像是( ).

图1

解析设物块的质量为m,斜面倾角为θ,物块与斜面间的动摩擦因数为μ,物块开始下滑时到斜面底端的距离为s0.当物块沿斜面下滑的位移s满足0≤s≤s0,即0≤x≤s0cosθ时,有mgsinθ－μmgcosθ,由几何关系知,可得为定值;当x＞s0cosθ时,物块在水平面上向右滑动,有为定值,故选项A 正确.

点评物块在斜面上运动时动能Ek随位移s变化率的绝对值表示物体在斜面上运动过程中受到的合力大小.题给出的图像描述的是物块的动能Ek与水平位移x的关系,根据物块沿斜面下滑的位移s与水平位移x的大小关系,将的表达式转换为的表达式,根据的表达式结合图像的物理意义,作出对图像的定性判断.

例3(2022年江苏卷)某滑雪赛道如图2 所示,滑雪运动员从静止开始沿斜面下滑,经圆弧滑道起跳.将运动员视为质点,不计摩擦力及空气阻力,此过程中,运动员的动能Ek与水平位移x的关系图像正确的是( ).

图2

解析设运动员质量为m,斜面倾角为θ,不计摩擦力和空气阻力,由题意可知运动员在沿斜面下滑过程中,根据动能定理有Ek＝mgxtanθ,可得,故运动员沿斜面下滑过程中的Ek-x图像为一条过原点的倾斜直线;圆弧切线的水平倾角θ先减小后增大,则运动员在圆弧轨道上运动过程中,Ek-x图像中曲线切线斜率的绝对值先减小后增大.综合判断可知选项A 正确.

点评本题给出的图像描述的是运动员的动能Ek与水平位移x的关系.运动员沿斜面下滑过程中其动能Ek与水平位移x的关系图像中切线斜率绝对值为.圆弧轨道可看成倾角θ连续变化的斜面,根据运动员在斜面上运动的特点,结合的物理意义,即可推知运动员在圆弧轨道上运动过程中Ek-x图像的分布情况.

2 Ek-t图像

Ek-t图像描述的是物体的动能Ek随时间t变化的关系.设物体合力做功的功率为P,在一段很短的时间Δt内物体动能的变化为ΔEk.由动能定理有PΔt＝ΔEk,可得.故Ek-t图像中直线或曲线某点切线的斜率的绝对值表示物体所受合力做功的瞬时功率P.

例4(2018年江苏卷)从地面竖直向上抛出一只小球,小球运动一段时间后落回地面,忽略空气阻力,该过程中小球的动能Ek与时间t的关系是( ).

解析设小球质量为m,不考虑空气阻力,小球在运动过程中受到的合力即为小球的重力mg.小球在上升过程中速度v1逐渐减小,由P1＝－mgv1知合力的功率逐渐减小,可知小球在上升过程中Ek-t图像为曲线,切线斜率的绝对值逐渐减小;小球在下落过程中速度v2逐渐增大,由P2＝mgv2知合力的功率也逐渐增大,小球下落过程中的Ek-t图像为曲线,切线斜率的绝对值逐渐增大,故选项A 正确.

点评物体动能变化的快慢与合力做功的快慢有关,即与合力的功率有关.以上分析中利用了Ek-t图像的物理意义,采用了定量与定性相结合的方法对图像的变化进行判断.

3 Ep-x 图像

Ep-x图像描述的是物体的重力势能Ep随竖直位移x变化的关系.设物体的质量为m,由重力做功与重力势能的变化关系有ΔEp＝－mgΔx,得－mg.故Ep-x图像某点切线的斜率的绝对值表示物体受到的重力大小.

例5(2020年全国卷Ⅰ)一物块在高3.0m、长5.0m 的斜面的顶端从静止开始沿斜面下滑,其重力势能和动能随下滑距离s的变化分别如图3中直线Ⅰ、Ⅱ所示,重力加速度g取10m·s－2.则( ).

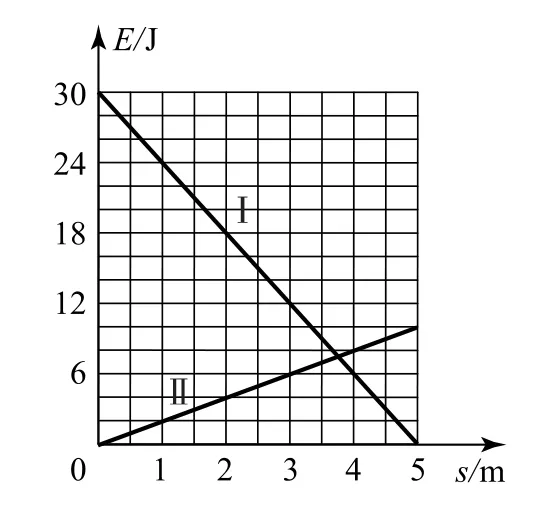
图3

A.物块下滑过程中机械能不守恒

B.物块与斜面间的动摩擦因数为0.5

C.物块下滑时加速度的大小为6.0m·s－2

D.当物块下滑2.0m 时机械能损失了12J

解析由图像知物块的机械能E＝Ek＋Ep是变化的,即机械能不守恒,选项A 正确.设斜面的倾角为θ,有,可知θ＝37°.图线Ⅰ为物体的重力势能Ep随物体沿斜面下滑的距离s的变化图线,其图像斜率,物块的竖直位移大小x＝ssinθ,由得mgsinθ＝6N,故m＝1kg.图线Ⅱ为物体的动能随位移变化图线,Ek-s图像斜率k2＝2N,为物体所受合力的大小,即mgsinθ－μmgcosθ＝2 N,可得μ＝0.5,选项B正确.物块沿斜面下滑时由牛顿第二定律有mgsinθ－μmgcosθ＝ma,得a＝2m·s－2,选项C错误.物块损失的机械能等于克服摩擦力做的功,即Wf＝μmgscosθ＝8J,选项D 错误.

点评物体重力势能随竖直位移的变化率等于物体受到的重力大小,要注意物块在斜面上运动的位移s与竖直位移x的大小关系.

4 Ep-t图像

Ep-t图像描述的是物体的重力势能Ep随时间t变化的关系.设物体质量为m,由重力做功与重力势能的变化关系有ΔEp＝－mgΔx,又由Δx＝vΔt,得.故Ep-t图像中直线或曲线某点切线的斜率绝对值表示物体重力做功的瞬时功率PG.

例6(原创)物体做自由落体运动,不计一切阻力,则在下落过程中物体的重力势能Ep随运动时间t的变化图像可能是( ).

解析设物体质量为m,某时刻竖直速度大小为v,则;自由下落的物体的速度v＝gt,故重力的功率PG＝mgv随时间增大而增大,可知选项B正确.

点评物体重力势能的变化量的绝对值等于重力做的功,重力势能随时间的变化率反映了重力势能变化的快慢,即重力的瞬时功率大小.

5 E-x 图像

E-x图像描述的是物体的机械能E随位移x变化的关系.设物体受到除重力之外其他力的合力大小为F其他,在一段很短的位移Δx内物体机械能变化为ΔE.由功能关系有F其他Δx＝ΔE,可得.故E-x图像中直线或曲线某点切线的斜率的绝对值表示物体受到重力之外其他力的合力大小.

例7(2019年全国Ⅱ卷)从地面竖直向上抛出一物体,其机械能E等于动能Ek与重力势能Ep之和.取地面为重力势能零点,该物体的E和Ep随它离开地面的高度h的变化如图4所示.重力加速度g取10m·s－2.由图中数据可得( ).

图4

A.物体的质量为2kg

B.h＝0时,物体的速率为20m·s－1

C.h＝2m 时,物体的动能Ek＝40J

D.从地面至h＝4m,物体的动能减少100J

解析Ep-h图像的斜率表示物体重力大小,即mg＝20N,可得m＝2kg,则选项A 正确;h＝0 时,Ep1＝0,则,可得v1＝10m·s－1,选项B错误;h＝2m 时,Ep2＝40J,则Ek2＝E2－Ep2＝90J－40J＝50J,选项C错误;设物体受到的阻力大小为Ff,E-h图像的斜率表示物体受除重力之外的其他力即阻力大小,有Ff＝;从地面至h＝4 m,物体的动能变化ΔEk＝W合＝－(mg＋Ff)h＝－100J,即物体的动能减少100J,选项D 正确.

点评机械能随位移变化图线斜率的绝对值为物体受到除重力之外其他力的合力大小,即为本题中物体受到的阻力大小.

6 E-t图像

由F其他Δx＝ΔE,得,即E-t图像中直线或曲线某点切线的斜率的绝对值表示物体受到的除重力之外其他力的合力做功的瞬时功率.

例8(原创)一小球从地面竖直上抛,经t0时间到最高点,后又落回地面,小球运动过程中所受空气阻力大小与速率成正比.下列关于小球运动的机械能E随时间t变化的图像可能正确的是( ).

解析小球的速率为v时受到的空气阻力大小为Ff＝kv.在小球上升过程中,其速率v越来越小,由知小球机械能的变化率的绝对值逐渐减小;在小球下落过程中,其速率v越来越大,故小球机械能的变化率的绝对值逐渐增大.选项C正确.

点评小球速率v与空气阻力Ff大小随时间t变化,小球的机械能随时间变化,但机械能随时间变化率的绝对值等于阻力的瞬时功率.

总之,分析与机械能有关的图像问题时,要善于从图像变化率着手,结合动能定理与功能关系、功率表达式,分析图像变化率的物理意义,进而求解问题.

(完)