形似质异 相得益彰
——例谈质点系动能定理与质心动能定理的应用
许冬保(特级教师、正高级教师)
(江西省九江市第一中学)
质点动能定理是中学物理课程中的重要内容.然而,有些力学问题,应用质点动能定理求解,会带来一些疑惑.质点系动能定理与质心动能定理作为质点动能定理的拓展,具有释疑解惑、优化思维品质的功能.二者形似质异,内涵不同,用于解题,相得益彰.
1 质点系动能定理
设质点系由N个质点构成,则第i个质点的动能变化量应等于作用于第i个质点的外力的功和内力的功之和,即Wi外+Wi内=ΔEki.
对i求和,得到质点系动能定理数学表达式为
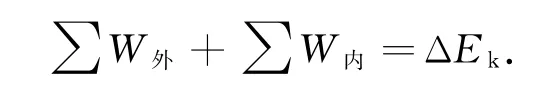
因此,作用于质点系所有外力所做的功与所有内力所做的功的总和等于质点系动能的变化量.
质点系动能定理适用于质点系,与质点动能定理一样,质点系动能定理也只能在惯性系中成立.其功包括内力功与外力功两部分,其中外力功中的位移为力的作用点的位移.
2 质心动能定理
质心是质点系的平均位置,是各质点以质量为权的加权平均位置.几何上质心是一个点,没有内部结构,在惯性系中不存在自身的转动.因此,质心的运动可以在某些方面代表整体的运动.
若质点质量及位置坐标分别为mi、ri,则质心位置一般公式为
对低速宏观世界中的一切物体,由质心运动定律有
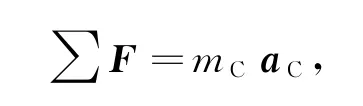
式中,∑F为系统受到的外力之和,aC为质心加速度.
上式两边点乘质心位移drC,有
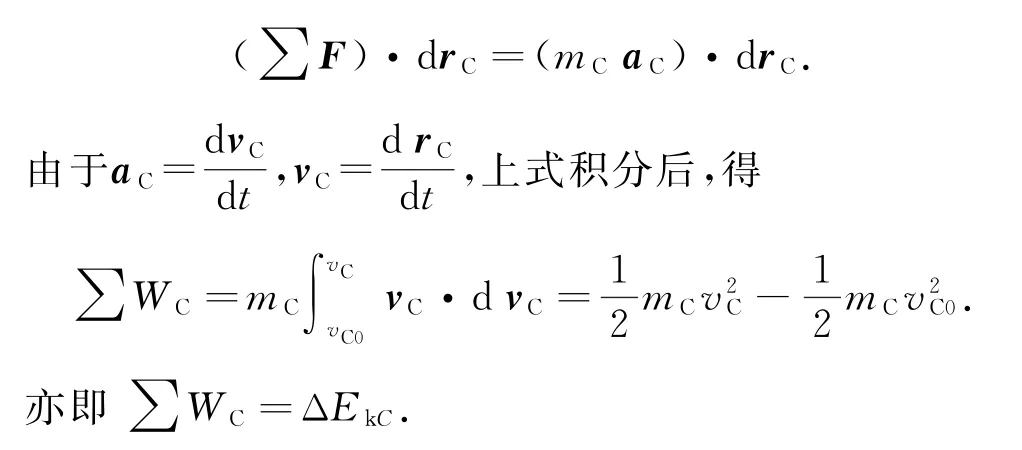
上式表明,合外力对质心所做的功等于质心动能的变化量.此为质心动能定理的数学表达式或质心动能方程.
质心动能定理描述的是作用于质心上的诸外力做的总功与质心动能变化之间的关系.显然,等号左边是所有外力做功的代数和,不含内力功;外力功的表达式中,合外力与质心位移的乘积的意思是将合外力平移到质心后对质心所做的功,该功并不一定对应真实的功,往往叫作虚功或质心功.外力功中的位移是质心的位移,不是力的作用点的位移;质心动能是指质心平动动能,不含转动动能.
3 应用分析
3.1 地面对运动员做功的质疑
例1一位质量为m的运动员从下蹲状态向上起跳,经Δt时间,身体伸直并刚好离开地面,速度为v.重力加速度为g,在此过程中( ).
A.地面对他的冲量为mv+mgΔt,地面对他做的功为
B.地面对他的冲量为mv+mgΔt,地面对他做的功为零
C.地面对他的冲量为mv,地面对他做的功为
D.地面对他的冲量为mv-mgΔt,地面对他做的功为零
解析设地面对运动员的冲量为I,取竖直向上为正方向,则由动量定理有I-mgΔt=mv,解得I=mv+mgΔt.
由于地面对人的支持力与地面垂直,且支持力的作用点未发生位移,因此,支持力对运动员不做功.选项B正确.
讨论该题的疑惑在于,既然地面对运动员未做功,但运动员为何获得了动能? 下面通过质点系动能定理及质心动能定理列方程进行分析.
1)质点系动能定理分析
运动员可视为质点系,若内力功为W,运动员重心(或质心)升高d.由质点系动能定理有W-mgd=,解得
2)质心动能定理分析
设运动员受到地面的支持力大小为FN,由质心动能定理有,解得
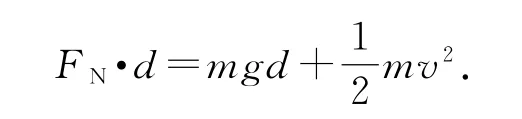
综上分析得W=FN·d.
此处FN·d并非功量.如上所述,实际上支持力FN的作用点并未发生位移,FN不做功;FN·d可理解为虚功.表达式W=FN·d的物理意义是内力功大小等于支持力与质心位移的乘积.类似的还有汽车牵引力做功的问题,分析方法相同.
3.2 刚体转动问题不宜用质心动能定理来处理
例2一长为L、质量不计的刚性硬杆,左端通过铰链固定于O点,中点及右端分别固定质量为m和质量为2m的小球,两球与杆可在竖直平面内绕O点无摩擦地转动.开始时使杆处于水平状态并由静止释放,如图1所示,当杆下落到竖直位置时,求在杆中点的球的速率.
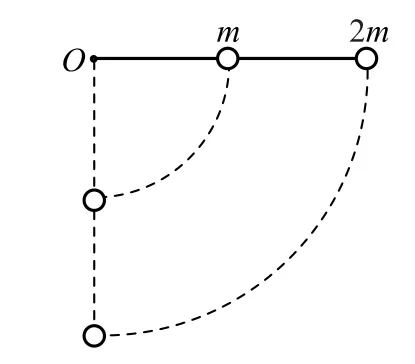
图1
解析两球转动的角速度相同,则由圆周运动角速度与线速度的关系知,杆中点的小球的速度为外端小球速度的一半.设中点的小球的速度大小为v,由质点系动能定理(或系统机械能守恒定律)有
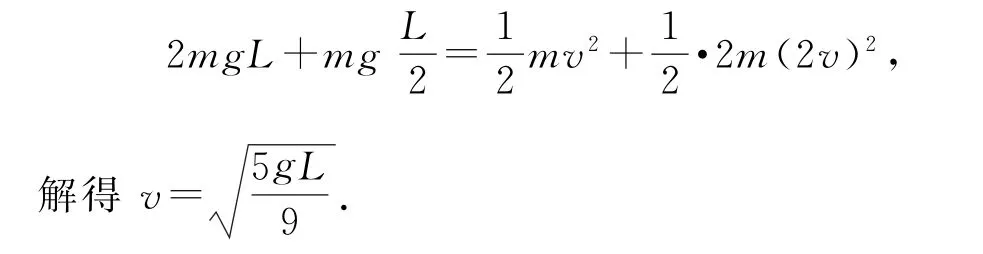
讨论若用质心动能定理求解,过程如下:找到两球的质心位置,由质心动能定理,有
可见,质心动能定理与质点系动能定理所求结果不同.原因何在? 原因是质心动能定理不适用于转动的情形.本题描述的是刚体的定轴转动,并非质点系的平动问题.
柯尼希定理表明,转动体的动能等于质心的动能与相对质心的动能(或相对动能)之和.计入相对动能,由质点系动能定理有

3.3 用两个动能定理联合处理问题更简洁
例3有两个质量均为m的小球,用长为2L的轻绳连接起来(球的直径相比L可忽略),置于光滑水平面上,绳恰好处于伸直状态,如图2所示,今用一个恒力F作用在绳的中点,F的方向水平且垂直于绳的初始长度方向,原为静止的两个小球因此运动.试问,在两个小球第一次相碰前的瞬间,小球在垂直于F作用线方向上的分速度为多大?
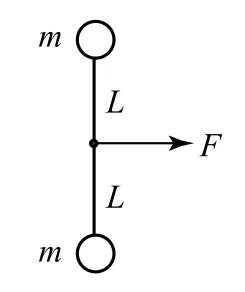
图2
解析 质点系动能定理
在F作用线方向(设为x方向)上,当绳与作用线成θ角时,如图3 所示,绳中张力为小球受到作用力大小为FT,x方向的分力为,故FTx也是恒量,小球在x方向的加速度为即小球在x方向上做匀加速运动.设两球第一次相碰前瞬间,小球的x方向分速度为vx,恒力F作用点已有的位移量为s,则小球在x方向位移为s-L,有
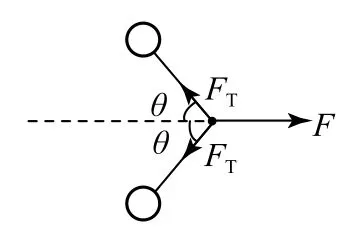
图3
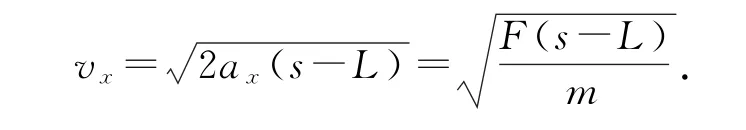
此时恒力F做的功为Fs.设小球垂直于x方向的分速度大小为vy,则由质点系动能定理有

质心动能定理
如图4所示,由质心动能定理有F(s-L)=2×.由质点系动能定理有联立求解,结果同上.
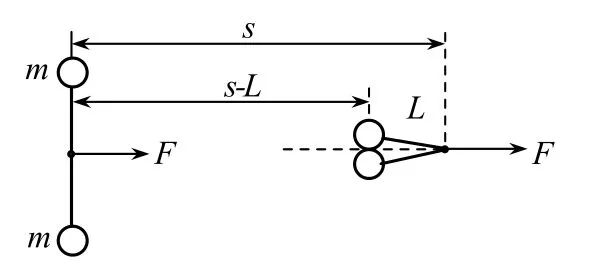
图4
点评对比两种求解方法,应用质点系动能定理与牛顿运动定律求解,过程烦琐;应用质心动能定理与质点系动能定理联合求解,过程简洁明了.
3.4 用质心动能定理处理问题更高效
例4如图5所示,水平面上3 个质量均为m的小物块,彼此相距d,在水平恒力F作用下,第1个物块由静止开始向右运动距离d,与第2个物块发生完全非弹性碰撞,二者共同运动距离d后,又与第3个物块发生完全非弹性碰撞.求水平面光滑和粗糙两种情况下碰撞后3个物块共同运动的速度.
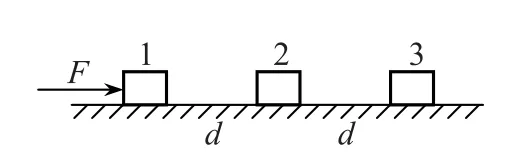
图5
解析质点系动能定理
水平面光滑.设第1个物块以速度v1与第2个物块发生碰撞,碰后共同速度为v2;第1、2物块组合体以速度v3与第3个物块发生碰撞,碰后3个物块共同运动的速度即系统的质心速度,设为vC.由质点动能定理有,由动量守恒定律有mv1=2mv2.同理,1、2整体与3发生碰撞过程,有
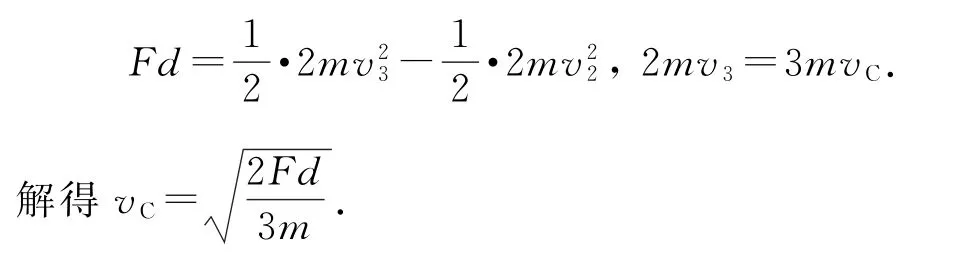
水平面粗糙.设第1个物块以速度与第2个物块发生碰撞,碰后共同速度为;第1、2物块组合体以速度与第3个物块发生碰撞,碰后3个物块共同运动的速度即系统的质心速度,设为.由动能定理有由动量守恒定律有.同理,1、2整体与3发生碰撞,有

质心动能定理

式中,物块1所受摩擦力对应系统质心位移为d,物块2所受摩擦力对应系统质心位移为
方程求解结果同上.
点评本题分别应用质点动能定理及质心动能定理建立方程求解.如果水平面光滑,考查第1、2物块的碰撞,则质心动能定理方程为;系统动量守恒定律方程为2mvC1=3mvC,所得结果相同.通过对比,体会应用质心动能定理解题的优越性.
3.5 2022年高考全国乙卷压轴题功能分析
例5(2022年全国乙卷)如图6-甲所示,一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上;物块B向A运动,t=0时与弹簧接触,到t=2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图6-乙所示.已知从t=0到t=t0时间内,物块A运动的距离为0.36v0t0.A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞.之后A再次滑上斜面,达到的最高点与前一次相同.斜面倾角为θ(sinθ=0.6),与水平面光滑连接.碰撞过程中弹簧始终处于弹性限度内.求:

图6
(1)第一次碰撞过程中,弹簧弹性势能的最大值;
(2)第一次碰撞过程中,弹簧压缩量的最大值;
(3)物块A与斜面间的动摩擦因数.
解析仅对第(2)问进行分析.
由系统动量守恒可求得B的质量为5m.设A、B之间相互作用的平均力为,由质点动能定理有
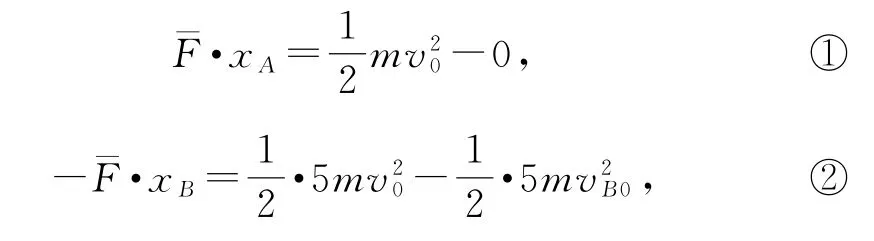
式中,vB0为碰前B的速度,由图知vB0=1.2v0.已知xA=0.36v0t0,则xB=0.792v0t0.
因此,弹簧压缩量的最大值
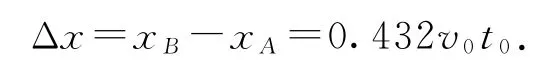
讨论审视上述过程,很难发现错误.可答案是错误的,原因何在?
抛开平均力,用积分式表示功量.对A,由质点动能定理有
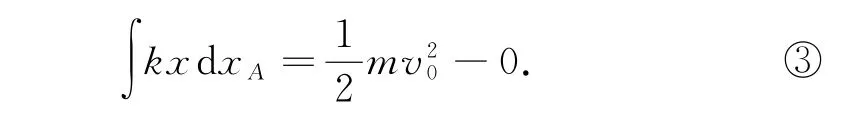
对B,由质点动能定理,有
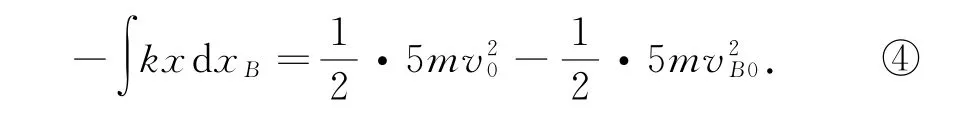
设0~t0时间内,B相对A的元位移为dx,即

联立式③④得
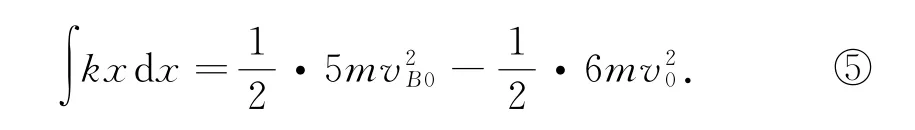
设0~t0时间内,弹簧压缩量为x,则式⑤左边为弹簧弹性势能
式⑤表明:弹簧弹性势能的增加等于系统动能的减少.若将弹簧与A视为系统建立质点系动能定理方程,应为

联立式④⑥求解,所得结果与式⑤相同.
再审视方程①②,不难发现,出现错误的原因是力对位移的平均值的理解有误,认为弹簧对物块A、B的平均力大小相等,而实际上弹簧弹力在两个不同的位移上,其力对位移的平均值不等.
综上,两个动能定理的联合使用,相得益彰,可使问题的分析更加深入,对概念的理解更加透彻,有效提高思维的深刻性、批判性和敏捷性.
(完)

