转动中的惯性
詹 凯 吴 滨
(1.首都师范大学附属中学 2.北京市101中学)
普通高中物理学习的运动学叫作“质点运动学”,学习的动力学也集中研究“质点动力学”.而牛顿第二定律在物体所受的力与其运动状态的变化之间建立了定量联系:F=ma,物体的受力F与加速度a之间的纽带就是物体惯性大小的量度——质量.
生活中,我们不可避免地会研究不能简化为质点的物体(将其模型简化为“刚体”)的运动.定量研究用多大的力能使转动的物体停下来? 转动物体具有的“动能”有多大? 滑冰运动员抱紧双臂为什么就可以转得更快? 等等.
研究物体转动的难点在于,物体上各个点转动时的角速度虽然相同,但线速度是不一样的.加速或减速转动的物体离转轴不同位置的质量微元,其加速度的大小并不相同,这就给我们的定量计算带来了困难.另外,通过滑冰运动员张开双臂和收紧双臂来控制转动角速度的实例也可以看出,物体转动时的惯性似乎不仅跟物体的质量有关,还跟质量分布有关.可见,物体转动时的惯性并不是一个恒定不变的量,这给研究物体的转动蒙上了一层神秘的色彩.
虽然转动惯量不是高中物理所要求的内容,但却是强基考试、物理竞赛中的基础知识与核心内容之一.有意参加强基考试和物理竞赛的同学,一定要将转动问题当作重中之重进行研学.
1 如何类比质点动力学,得出“转动惯量”?
刚体作为一个质点系,在定轴转动时它的动量p等于质心动量pC.刚体每一无穷小区域都可处理成点部位,所含质量记为mi,定轴转动时刚体的动能为
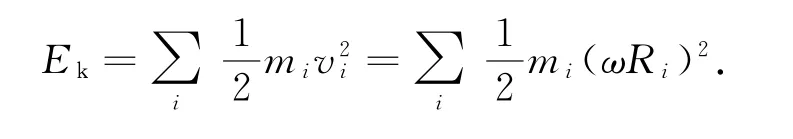
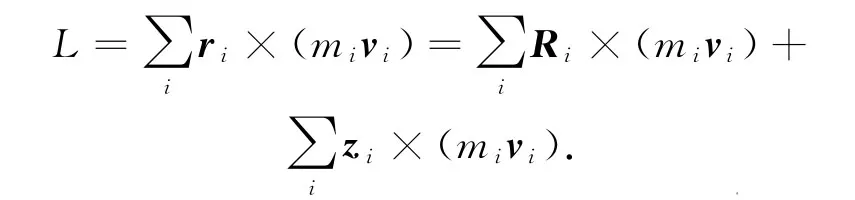

图1
等号右端第一项的方向沿z轴,实为Lz,第二项的方向平行于xOy平面,实为Lxy,定轴转动问题主要讨论刚体绕z轴转动情况的变化,即角动量的z轴分量.
Lz的标量式为
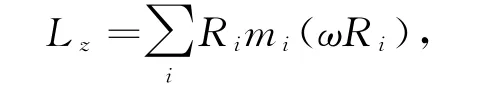
可表述成Lz=Iω,与质点动量p=mv的结构形式相似,其中I仍与m对应.刚体定轴转动时的两个动力学量Ek和Lz都与转动惯量I有关,I由给出,对于物质连续分布的刚体,可通过积分来完成求和.
2 如何计算常见刚体的转动惯量?
例1质量为m、长度为L的均质杆,绕着垂直于杆所在平面并通过质心的轴旋转,求杆的转动惯量.
解析如图2 所示,根据转动惯量的定义式进行积分.
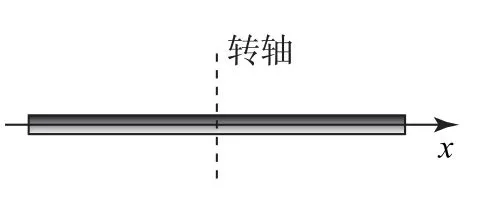
图2

一些常见的刚体的转动惯量如表1所示.

表1
根据转动惯量的定义式,在计算连续体的转动惯量时,理论上应当应用积分.但是积分计算对于一般中学生来说是个难点.是否有别的办法避免烦琐的积分运算呢?
3 转轴不在特殊位置时,有什么办法计算刚体的转动惯量?
若两转轴平行,距离为d,其中一轴过质心,质量为m的刚体对过质心的轴的转动惯量为IC,则刚体对另一轴的转动惯量为I=IC+md2,这叫作“平行轴定理”.显然,刚体相对各平行轴的不同转动惯量中,过质心轴的转动惯量最小.
薄板(厚度无限小)相对与它垂直的坐标轴的转动惯量,等于薄板对于板面内两互相垂直轴的转动惯量之和,即Iz=Ix+Iy.这叫作“垂直轴定理”,也叫作“正交轴定理”.其适用条件是x、y、z轴过同一点,且互相垂直,z轴垂直于板面,x、y轴在板面内,如图3所示.
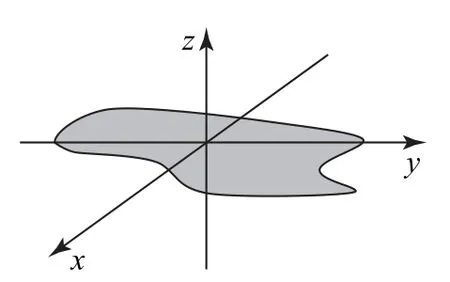
图3
例2计算以下物体绕轴的转动惯量.
(1)均质杆,质量为m,长度为L,绕着垂直于杆所在平面并通过质心的轴旋转.
(2)均质正三角板,质量为m,边长为b,绕着垂直于板平面并通过质心的轴旋转.
解析(1)例1通过积分方式得到答案.此处利用量纲关系以及平行轴定理联立求解.
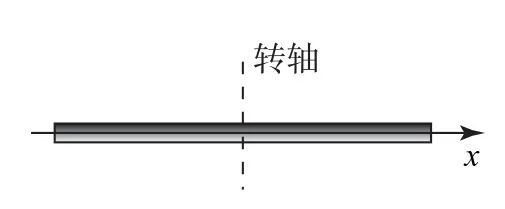
图4
(2)如图5所示,将大正三角板分成4个相等的小正三角板,每个小正三角板的边长为根据转动惯量与质量、长度的量纲关系可知,小正三角板绕着垂直于板平面并通过质心的轴旋转时的转动惯量I′,与大正三角板绕着垂直于板平面并通过质心的轴旋转时的转动惯量I之间的关系为

图5
若假设大正三角板的转动惯量I=λmb2,则小正三角板的转动惯量.根据平行轴定理,3个角上的小正三角板绕着中间小三角板中心轴的转动惯量I″为.4个小正三角板组合成大正三角板,则I=I′+3I″,
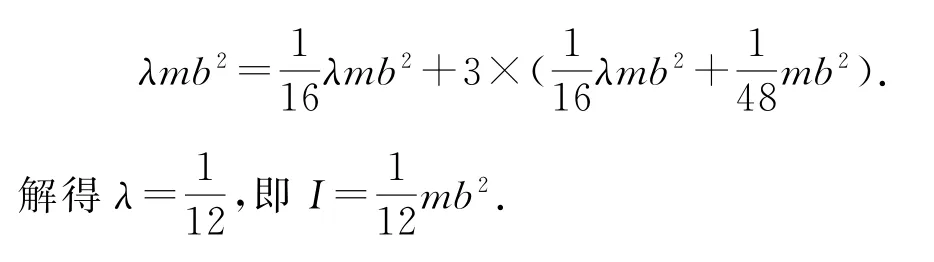
例3均质正方形薄板质量为m、各边长为a.如图6所示,在板平面上设置过中心O的转轴MN,求板相对该轴的转动惯量I.
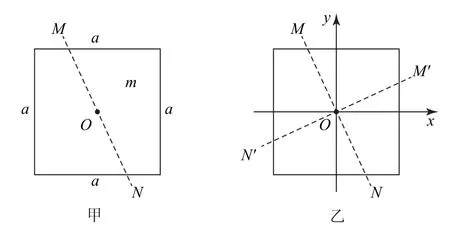
图6
解析板平面上薄板沿x、y轴转动时的转动惯量与例1中的均质杆绕垂直于杆所在平面并通过质心的轴的转动惯量一样.再结合垂直轴定理,可迎刃而解.在板平面上设置过O点且与MN垂直的M′N′轴,相应的转动惯量记为I′.根据对称有I=I′.在板平面上建立xOy坐标系,相对于x、y轴转动惯量相同,即.再根据垂直轴定理,得I+I′=Iz,Ix+Iy=Iz,其中,Iz是板绕着过O点且垂直于板平面的转轴的转动惯量.于是有I+I′=Ix+Iy,得
点评由例2、例3两道例题可以看出,如果能巧用平行轴定理和垂直轴定理,可以省掉大量的积分计算.这样就大大降低了计算转动惯量的难度.
4 如何打棒球,才能不手麻?
例4如图7所示,质量为m的刚体,其质心C到悬挂点P的距离为rC.以水平力F打击该刚体上的O点,若打击点O选择合适,则打击过程中轴对钢体的切向力Fτ为0,该点O称为打击中心,求打击中心到轴的距离r0.(设刚体绕与P点转轴平行且过质心的转轴的转动惯量为IC)
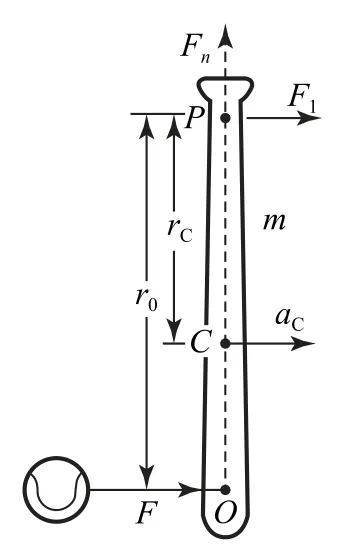
图7
解析刚体的质心在水平方向有加速度,若转动引起的质心的加速度恰由力F提供,则悬挂点P就不需要提供水平方向的切向力.刚体绕P点的转动惯量I=IC+mr2C.刚体在水平力的力矩Fr0的作用下做定轴转动.设棒的角加速度为β,则转动动力学方程为Fr0=Iβ,刚体质心的切向加速度为aC=βrC,若P点对刚体无水平作用力,则质心运动方程为F=maC=mβrC.联立消去β得
点评从上述解析过程可以看出,利用转动惯量I解决刚体的动力学问题时,也有类似“刚体转动的牛顿第二定律”形式,其中力被力矩替代,质量被转动惯量替代,加速度被角加速度替代.另外,从例题结果可以看出,悬挂于端点的长为L的均质细杆,打击处时,悬挂点P不受力.棒球运动员在击打棒球时,如果击球点在打击中心附近,则手受到棒的作用力最小,这样手就不会感觉到强烈的疼痛.
5 花样滑冰运动员是如何控制转速的?
花样滑冰运动员在比赛中经常做出这样的动作——伸开双臂原地转圈时,双臂逐渐抱紧身体的过程中,转动的角速度越来越大.这是为什么呢? 结合前述多个问题的讨论,可以给出该问题的定性解释.
运动员在转动过程中,冰刀与冰面之间的摩擦力很小,力臂也很小,可以视为几乎不受力矩作用.类比不受外力作用的质点动量守恒,可以得出结论——运动员在转动过程中角动量守恒.此时,抱紧双臂的过程中,运动员质量分布逐渐靠近转轴,转动惯量减小,要保持角动量不变,则需增大转动的角速度.
6 阿特伍德机的动力学问题
例5如图8所示的装置为阿特伍德机,即一轻绳绕过质量为m、半径为R的质量分布均匀的圆盘形定滑轮,绳的两端分别系有质量为m1和m2的物体,m1>m2,滑轮轴上受到的摩擦阻力可忽略.试求两物体运动的加速度和两侧绳上的张力.假定绳子不能伸长,绳与滑轮之间摩擦力足够大以至于绳与滑轮之间无相对滑动,重力加速度大小为g.
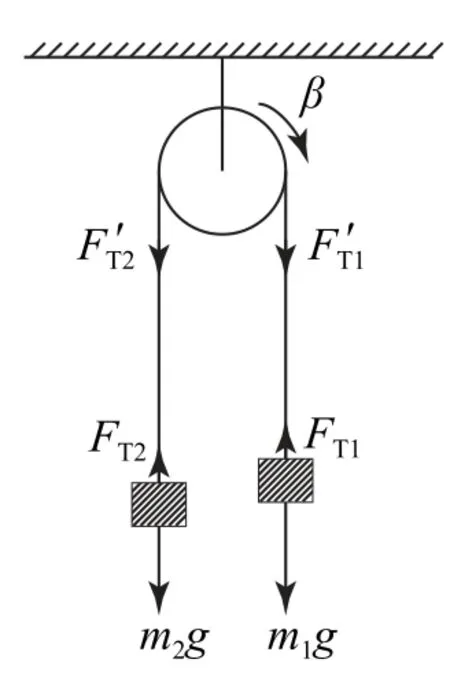
图8
解析由于滑轮有转动惯量,因此两侧物体加速运动时,滑轮加速转动,绳子两侧张力肯定不同,否则滑轮所受合力矩为0.对两物体和滑轮分别列动力学方程,联立求解即可.
设两根绳中的张力分别为FT1、FT2,两物体运动时的加速度大小为a,滑轮转动时的角加速度大小为β,根据牛顿第二定律以及转动定理知m1g-FT1=m1a,FT2-m2g=m2a,FT1R-FT2R=Iβ.圆盘转动时的转动惯量,a与β之间的运动辅助方程为a=βR.联立以上方程可得
点评从以上结果可以看出,若滑轮质量可忽略不计时,即上述3个表达式中m→0,则a=,这正是课内学习牛顿运动定律处理简单的滑轮连接的两物体加速度与拉力问题的结果.但是本题的结果更具有一般性,一般性的结果在m→0的情况下能回归到已知的结果中去,正说明本题结果的正确性,这也是我们检查结果是否正确常用到的方法.
转动问题在生活中广泛存在.在研究转动问题时,衡量物体惯性的物理量为转动惯量,物体的转动惯量不仅跟其质量有关,还与转动的方式、转轴的位置等有关.转动问题中的转动惯量,与质点动力学中的“平动惯量”,即物体的质量,有着异曲同工之妙.在学习转动问题时,要不断将转动、平动问题进行对比和联系,体会其中的不同点与相同点,这有助于我们对牛顿力学体系获得更深、更广的理解.
(完)

