应用“微元累积法”解决物理问题,培养科学思维素养

张云莹 姜 葛

(北京市昌平区教师进修学校)

微元累积法是物理学中一种重要的思想方法,是微积分思想在解决物理问题时的应用和体现.微元累积法包含微元和累积两个过程,微元过程的思想是:对于较复杂的物理变化或过程,通常先把整个过程分割成若干个小区间,认为每一小区间内研究的量不变,这样就可以把变化的、物理规律不适用的过程转化为不变的、物理规律适用的微元过程.将所有的小区间内的问题都解决后,再把全部结果累积叠加,这个过程就是累积过程.

由于累积过程会用到积分知识,所以中学阶段往往把它转化为求相应图像所围图形的“面积”,此时“面积”起到了数学和物理间的桥梁作用.

1 物理量对时间的累积

1.1 速度对时间的累积

我们知道,做匀速直线运动的物体的v-t图像是平行于t轴的一条直线,在Δt时间内物体的位移为Δx＝vΔt,在量值上等于阴影标记矩形的面积,如图1所示.

图1

当物体做匀变速直线运动时,其v-t图像为一条倾斜的直线,如图2-甲所示.这时物体在Δt时间内的位移还能否用“面积”表示呢?

如果我们像图2-乙那样,把物体的运动分成6小段,每小段起始时刻物体的瞬时速度由相应的纵坐标表示,在每一小段内,可粗略认为物体以这个速度做匀速直线运动.因此,我们以每小段起始时刻的速度乘以时间,近似地当作各小段内物体的位移.在v-t图像中,各段位移可以用一个又窄又高的小矩形的面积表示.6个小矩形的面积之和近似地代表物体在整个运动过程中的位移.

当然,如果以这6个小矩形的面积之和代表物体在整个过程中的位移,显然比真实值要少.为了精确一些,可以把运动过程划分为更多的小段,如图2-丙所示.用所有这些小段的位移之和代表物体在整个过程中的位移就精确得多.小矩形越窄,所有小矩形的面积之和就越接近物体的位移.

可以想象,如果把整个运动过程分割得非常非常细,很多很多小矩形的面积之和就能非常精确地代表物体的位移了.这时,很多很多小矩形顶端的“锯齿形”就看不出来了,这些小矩形合在一起成了一个梯形,如图2-丁所示.这个梯形的面积就代表做匀变速直线运动的物体在Δt时间内的位移大小.

图2

上面这种分析问题的方法具有一般意义,原则上对于任意形状的v-t图像都适用.如图3所示的运动物体的位移大小,仍然可用处理匀变速直线运动的方法——“先微元再累积”,位移的大小仍可用v-t图像与横轴所围图形的面积来表示.

图3

1.2 加速度对时间的累积

物体的加速度也可以随时间连续变化,那么加速度对时间的累积又代表哪个物理量呢?

我们知道,物体做匀变速直线运动时,加速度不变,a-t图像是一条平行于t轴的直线.由匀变速直线运动的速度公式可知Δv＝aΔt,即加速度对时间的累积为速度的变化量,累积结果可用a-t图像的面积表示,如图4所示.

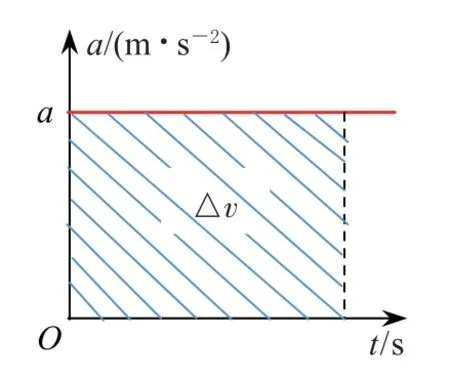
图4

对于做变加速直线运动的物体,其a-t图像的面积是否还表示速度的变化量呢?类比v-t图像求位移的方法可知,做变加速直线运动的物体,其a-t图像的面积仍然表示物体速度的变化量.

例1(2012年北京卷,有改编)某摩天大楼中有一部直通高层的客运电梯,已知电梯在t＝0 时由静止开始上升,电梯运行时的加速度a随时间t变化的a-t图像如图5所示.求:

(1)0～2s内电梯的速度的变化量;

(2)该电梯上升过程中的最大速度.

解析(1)电梯在0～2s内做变加速直线运动,由前面的学习我们知道,做变加速直线运动的物体,其a-t图像的面积表示速度的变化量.由此得,电梯在0～2s内速度的变化量为a-t图像第1个三角形的面积,即有

(2)t＝0时,电梯的速度为0;在0～12s内,电梯的加速度均为正值,即电梯的速度在增加,所以t＝12s时,电梯的速度最大.电梯的最大速度即为第1个梯形的面积,有

1.3 力对时间的累积

冲量是描述力对时间累积效应的物理量,其定义式I＝Ft适用于求恒力的冲量.如果在时间t内,作用在物体上的力是变化的,就要把整个运动过程分成很多很短的时间间隔Δt,以至在Δt时间内,可以认为力是不变的,用这段时间内的作用力乘以这段时间,则力的冲量为FiΔt,t时间内的冲量等于所有小段力的冲量的矢量和,即I＝∑FiΔt.如果物体做直线运动,求和的结果可用F-t图像与横轴所围图形的面积表示.

例2质量为2kg的物体,受到如图6所示的变力F的作用,从静止开始沿光滑水平面做直线运动.求5s末物体的速度大小.

图6

解析物体在变力F的作用下将做变加速直线运动,在5s内力F的冲量在量值上等于三角形的面积,即.对物体应用动量定理有I＝mv－0,故

1.4 电流对时间的累积

我们知道,电流定义为单位时间内通过导体横截面的电荷量,即.当Δt→0时,q-t图像上某一点的斜率即为电流i.如果知道电流随时间的变化规律,能否反过来求得通过导体横截面的电荷量呢?

根据Δq＝iΔt可知,电流对时间的累积表示通过导体横截面的电荷量.如果电流是变化的,根据微元累积思想可知,任意i-t图像与横轴所围图形的面积都表示通过导体横截面的电荷量.

例3在观察电容器的充、放电实验中,电路如图7-甲所示.先使开关S与1端相连,电源向电容器充电;充电完成后把开关S掷向2端,电容器通过电阻R放电,电流传感器将电流信息传入计算机,屏幕上显示出电流随时间变化的I-t图像如图7-乙所示.

图7

(1)图7-乙中竖立的狭长矩形(在图的最左边),它的面积的物理意义是什么?

(2)怎样根据I-t图像估算电容器在整个放电过程中释放的电荷量?

解析(1)根据前面的分析我们知道,电流对时间的累积表示通过导体横截面的电荷量,量值上等于I-t图像与t轴所围图形的面积.最左边的狭长矩形的面积可近似表示在0～0.1s时间内通过电阻R的电荷量,实际通过电阻R的电荷量要比这个狭长矩形面积略大.

(2)整个过程中面积的计算可借鉴测定分子直径实验的经验,已知每一小方格代表的电荷量为

然后再数一数图线与横轴所围成的图形中有多少个这样的小方格,大于半个的算一个,小于半个的不算,假设数后的结果为N,那么电容器在整个放电过程中释放的电荷量为Q＝Nq1.

2 物理量对空间的累积

2.1 力对空间的累积

功是描述力对空间累积效应的物理量,其定义式W＝Fx,适用于求恒力的功.如果在位移x内,作用在物体上的力是变化的,就要把整个运动过程分成很多很短的位移Δx,以至在Δx内,可以认为力是不变的,用这段时间内的作用力Fi乘以这段位移Δx,则力的功为Wi＝FiΔx,x位移内的功就等于这些小段力的功的标量和,即W ＝∑FiΔx.

如果知道了物体所受外力F随位移x的变化关系,则以位移为横轴,力为纵轴,作出F-x图像,这样F-x图像与横轴所包围图形的面积在量值上代表了力的功.因此,求功就变成了求F-x图像的面积.

例4如图8所示,某同学用一外力作用于劲度系数为k的轻弹簧上,使弹簧缓慢发生形变,形变量为Δx,弹簧始终在弹性限度内.求在这一过程中,该同学克服弹簧弹力所做的功W.

图8

解析该过程中,弹簧的弹力为变力,如何将变力做功转化为恒力做功,以便用功的定义式求解呢? 前面我们讲到,将该过程分割成若干个小区间,每个小区间内弹力可近似看作恒力,在每个小区间内应用功的定义求解,然后再把所有小区间累积起来,得到整个过程弹力所做的总功.同样,我们可以用“面积”表示累积的效果.

由胡克定律可知,弹簧弹力的大小与弹簧的形变量成正比,所以弹簧弹力F与形变量Δx的图像如图9所示.克服弹力做功W在数值上等于图像中阴影部分图形的面积,即

图9

当然,对于任意变力,F-x图像所围图形的面积在数值上均等于力F所做的功.

2.2 电场强度对距离的累积

在匀强电场中,电势差U与电场强度E之间满足U＝Ed的关系,即匀强电场中两点间的电势差等于电场强度与这两点沿电场方向距离的乘积.在匀强电场中,电场强度E随沿电场方向的位置x变化的图像为平行于x轴的直线,则其两点间的电势差即图像与x轴所包围图形的面积,如图10-甲所示.

对于非匀强电场,我们可以将整段距离d分成无数个很短的距离Δd,在每一段Δd中,电场强度Ei可以认为是恒定的,因此该段两点间电势差可以表示为ΔU＝EiΔd,即图像中小矩形的面积.因此,整段距离d两点间电势差U为每一段电势差ΔU的累积求和,即图线与x轴所包围图形的面积,如图10-乙所示.

图10

例5(2013年上海卷)半径为R、均匀带正电荷的球体在空间产生球对称电场,场强大小沿半径分布如图11所示,图中E0已知,Er曲线下O～R部分的面积等于R～2R部分的面积.

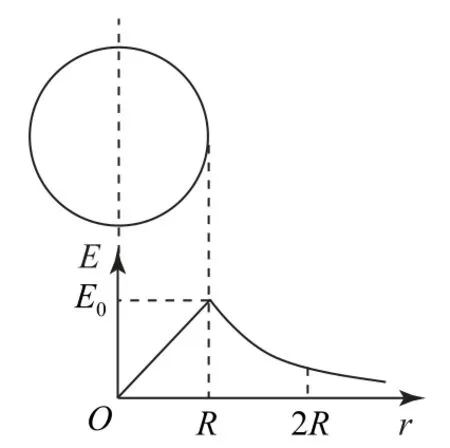
图11

(1)写出E-r曲线下面积的单位;

(2)已知带电球在r≥R处的场强式中k为静电力常量,该均匀带电球所带的电荷量Q为多大?

(3)求球心与球表面间的电势差ΔU.

(4)质量为m、电荷量为q的负电荷在球面处需具有多大的速度可以刚好运动到2R处?

解析两点间电势差等于电场强度对空间距离的累积,因此E-r曲线下的面积即电势差.

(1)根据分析可知电势差单位为伏特(V).

(2)根据图像可知,r＝R处场强因此

(3)E-r曲线下O～R部分的面积等于球心与球表面间的电势差ΔU,因此

(4)E-r曲线下O～R部分的面积等于R～2R部分的面积,因此球面处与2R处之间的电势差

负电荷刚好运动到2R处的过程中,根据动能定理有

2.3 磁感应强度对面积的累积

为了形象地描述磁场的大小和方向,人们引入了磁感线.当考查磁场中磁感线条数在某一曲面上的积累效果时,引入磁通量的概念,定义通过某一曲面磁感线的条数为这一曲面的磁通量,简称磁通,用字母Φ表示.

如图12-甲所示,磁感应强度为B的匀强磁场中,有一面积为S的平面,其在垂直磁场方向的投影面积为S⊥.可以看出,通过平面S的磁感线条数与通过平面S⊥的磁感线条数相同,则磁通量

其中θ为平面法线与磁场方向的夹角.

如图12-乙所示,磁场为非匀强磁场,曲面也不是平面,而是一个任意大小的有限曲面,在计算通过整个曲面的磁通量时,我们可以利用微元累积法,把整个曲面分成无限多个微小面元ΔS,每个ΔS可近似看成平面,且通过此面元的磁场可近似看成匀强磁场,则磁通量表示为

图12

由于曲面上每一个面元的法向事先规定,因此,磁通量可正可负,它表示磁感线穿过曲面的方向.磁通量这一概念的提出,不仅为我们提供了从空间区域积累的角度认识磁场的新视角,还为电磁感应现象的研究与应用打下了坚实的基础.

请读者思考:在电场中可否引入类似于磁通量的“电通量”呢?

例6(2018 年北京卷)静电场可以用电场线和等势面形象描述.

(1)请根据电场强度的定义和库仑定律推导出点电荷Q的场强表达式;

(2)点电荷的电场线和等势面分布如图13所示,等势面S1、S2到点电荷的距离分别为r1、r2.我们知道,电场线的疏密反映了空间区域电场强度的大小.请计算S1、S2上单位面积通过的电场线条数之

图13

解析(1)在距Q为r的位置放一电荷量为q的检验电荷.由库仑定律知检验电荷受到的电场力.根据电场强度定义

2.4 气体的压强对体积的累积

压缩一定质量的气体,外界要克服气体的压强对气体做功,根据功的定义W＝Fl知,W＝Fl＝pSl＝pV.由此可知,压强p对体积V的累积效果表现为功.当气体体积减小时,外界对气体做功;当气体体积增大时,气体对外界做功.

例7一定量的理想气体的p-V图像如图14所示,气体状态经历了A→B→C变化过程.则气体在状态C的内能________气体在状态A的内能(填“＞”“＜”或“＝”).在上述过程中,气体需_________(填“吸热”或“放热”),它与外界交换的热量的绝对值为________J.

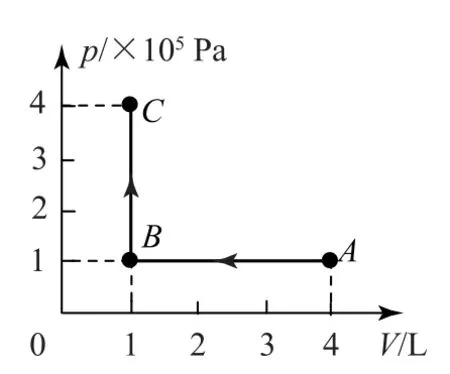
图14

解析由p-V图像可知,在A、C两状态,气体的pV值相等,由理想气体状态方程可知,A、C两状态的温度相等,则气体在两状态的内能相等.A→B过程为等压过程,气体体积减小,外界对气体做功W＝Fl＝pSl＝pV＝300J;B→C过程是等容变化,气体不做功.在整个过程中,由热力学第一定律U＝W＋Q,可知Q＝U－W＝0－300J＝－300J.由此可知,在整个过程中气体对外放热,放出的热量为300J.

3 并非所有的累积都有意义

当一个物理量对另一个物理量累积时,其累积结果不一定都有物理意义.

在如图15-甲所示的电路中,调节滑动变阻器的滑片P,通过定值电阻R上的电流I和其两端的电压U均在变化.由欧姆定律可知,U与I成正比,U-I图像如图15-乙所示.

图15

由于P＝UI,由上面的“经验”容易联想到,在UI图像中,图线与I轴所围成的图形的面积为功率P.事实上并非如此.我们找到图线中的一点,该点对应的横、纵坐标分别为I1、U1,此时R消耗的电功率为P1＝U1I1,对应图15-丙所示的矩形面积.究其原因是功率P不是电压U对电流I累积的结果,它等于电流和电压瞬时值的乘积.

(完)