地震作用下高填减载明洞土拱形态及衬砌结构动力响应研究

尤著刚，李盛，何川，马莉，王起才，贾涛

（1.兰州交通大学土木工程学院，甘肃 兰州 730070；2.西南交通大学土木工程学院，四川 成都 610031；3.成昆铁路有限责任公司，四川 成都 610081）

引言

高填减载明洞是近年来出现的一种新型地下结构，它可以在铁路（公路）建设的同时，重新整合土地资源，缓解城市用地紧张，增加城市用地面积，已在我国西北黄土高原地区交通基础设施建设中得到广泛应用，许多学者对其进行了大量研究［1－6］。土拱作为高填减载明洞中荷载传递的媒介，使结构周围土压力产生重分布，改善了结构受力。

已有诸多学者对静载和动载作用下的土拱形态进行了研究，主要集中在桩承式路堤上。杨涛等［7－8］通过建立弹塑性有限元模型，研究了静载作用下桩承式路堤中的土拱形态和交通动载作用下土拱形态的演变。赖汉江等［9－10］采用颗粒流分析程序PFC2D建立了桩承式路堤分析模型，通过接触力链研究了土拱形态及其演变规律，并基于路堤中应力偏转规律，分析了土拱随桩土相对位移的形成规律。莴瑞等［11］通过自制平面应变模型，对不同桩间距下沙填料桩承式路堤的宏观土拱形态及其演化现象行了研究。毕宗琦等［12］通过循环加载下的活动门实验，并结合粒子图像测速法（PIV），分析了土拱的结构形态、位移场和竖向应力变化规律。付海平等［13］基于室内模型试验和颗粒流软件PFC2D，研究了桩承式路堤中的“土拱结构”形态及其演化规律。然而，西北黄土地区地震活动频繁，建设在该地区的高填减载明洞势必会受到地震荷载的影响，静载作用下形成的土拱形态将发生改变。目前对于地震作用下高填减载明洞中减载的关键因素—土拱形态演变的研究却鲜有报道。

另外，地震作用下土拱形态的改变势必引起明洞衬砌结构的动力响应。目前，已有许多学者对静载和地震作用下的隧道结构内力进行了研究，李心熙等［14］依据某沉管隧道暗埋段，建立了有限元动力分析模型，对隧道刚度变化段各关键截面在静力和地震荷载下的内力及变形响应特性进行了研究。王祺等［15］以某软土地区超浅埋盾构隧道工程为依托，利用动力时程法对盾构隧道在竖向及水平向地震作用下的内力和变形规律进行了研究。郭军等［16］利用FLAC3D软件对公路隧道明洞结构进行了抗震计算，得出了衬砌结构的内力响应规律，并对衬砌结构在不同填土高度下的安全性进行了研究。于辉等［17］采用有限元软件ABAQUS，通过使用动力时程分析和拟静力分析方法，研究了穿越不同性质地层隧道结构的地震响应。赵密等［18］以拟静力有限元数值模拟结果为依据，对比验证了Wang、Park和Bobet这3种解析方法在不同隧道衬砌厚度条下的内力预测精度，并分析了误差的来源。陈之毅等［19］采用概率密度演化法，计算了随机地震作用下隧道结构变形响应的概率分布，并引用变形指标对隧道衬砌结构的抗震性能进行了评估。梁建文等［20］采用整体强制反应位移法对某地铁盾构隧道结构进行了抗震分析。陈清军等［21］通过建立地铁车站－隧道－土相互作用的三维整体有限元模型，探讨了地铁车站－隧道－土相互作用体系的地震反应规律。

目前，关于静载作用下土拱形态以及地震作用下隧道动力响应的研究已取得了一系列成果，而对地震作用下高填减载明洞的土拱形态变化以及由此引起的动力响应却鲜有报道。因此，文中利用有限差分软件FLAC3D，建立高填减载明洞动力分析模型，确定回填土中土拱形态，并对地震作用下回填土中土拱形态的变化及其引起的衬砌结构动力响应进行研究。

1 数值模拟

1.1 模型建立及测点布置

当模型的边界尺寸是明洞高度或宽度的3～5倍时，可认为计算结果不受边界效应的影响［22］，文中采用FLAC3D建立的高填减载明洞分析模型如图1所示。模型底部地基厚33 m，开挖沟槽宽度13.8 m，明洞高度11 m，宽度12.8 m，洞顶对称铺设的EPS板宽度12.8 m，厚度2 m，洞顶以上填土高度30 m，分4层回填，前两层回填高度为10 m，后两层回填高度为5 m。模型建立完成后，施加静力分析所需的边界条件：顶部无约束，四周和底部位移全约束。静力计算完成后，施加动力分析所需的自由场边界［23-24］，如图2所示。同时，为确保此次模型计算结果的准确性［25］，按照式（1）对模型网格进行划分：

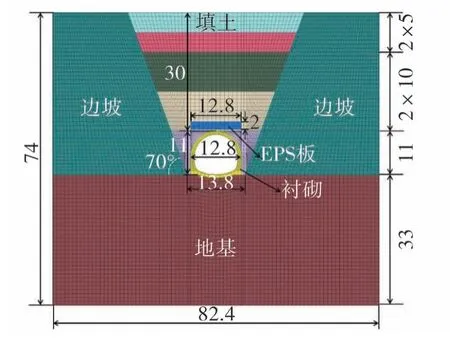
图1 高填减载明洞模型图（单位：m）Fig.1 Model for a high-filled cut-and-cover tunnel（Unit：m）

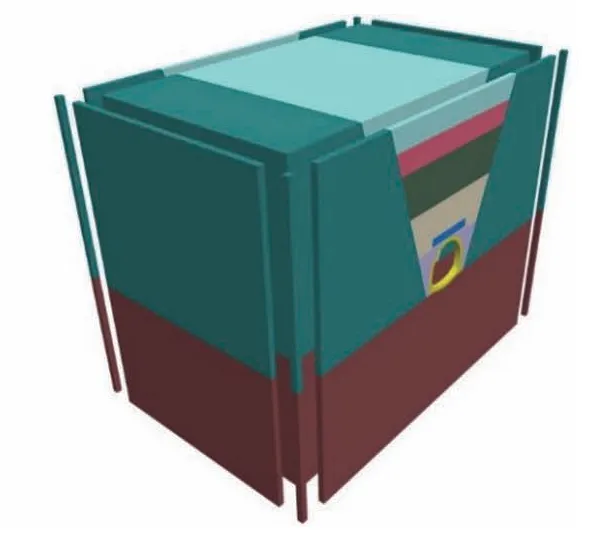
图2 模型自由场边界Fig.2 Free field boundary model

式中：Δl为最大模型网格尺寸；λ为地震波高频部分对应的波长。文中所采用地震波高频部分对应的波长λ为8.35 m，按照式（1）计算后，模型网格最大尺寸为1.04 m。

此外，为监测静载及地震过程中明洞周围的土压力和衬砌的结构内力，在模型中布置了一系列监测点，如图3和图4所示。图3中，A－A截面编号为－4～4的监测点用以测量洞顶的竖向土压力，B－B截面内编号－1～－6和C－C截面内编号为1～6的监测点用以监测明洞两侧水平土压力，D－D截面内未编号的测点用以监测不同填土深度处的竖向土压力。图4中布置在衬砌结构不同位置处的测点用以监测衬砌结构的轴力和弯矩。

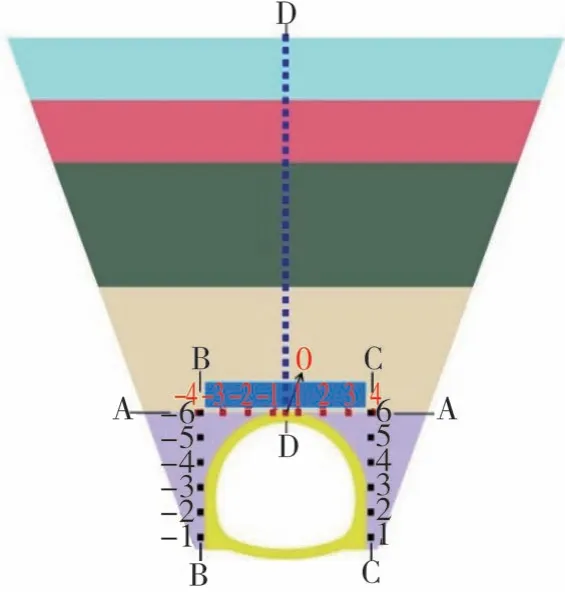
图3 土压力监测点布置Fig.3 Arrangement of earth pressure monitoring points

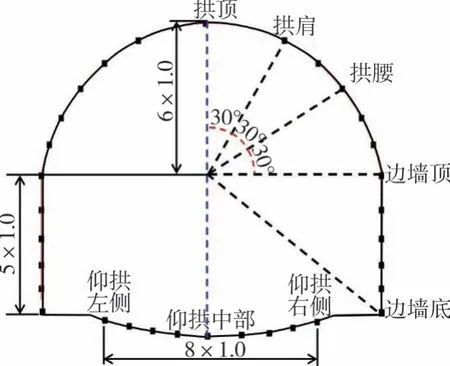
图4 衬砌结构内力监测点布置Fig.4 Arrangement of internal force monitoring points of lining structure

1.2 材料参数

1.2.1 EPS板参数设置

明洞顶铺设EPS板可以起到很好的减载效果［26］。因此，文中采用密度为20 kg/m3的EPS板作为减载材料。图5是通过室内单轴压缩实验获取的EPS板应力应变关系曲线。

由图5可以看出EPS板应力应变关系曲线在整个应变范围内主要分为弹性、塑性和硬化3个阶段［27］。此次计算对EPS板赋予弹性本构模型。静载及地震作用计算过程中，EPS的压缩变形会不断变化，导致其力学参数也不断改变，因此，文中提出了一种根据相应应变自动调整EPS力学参数的方法。具体实施步骤如下：

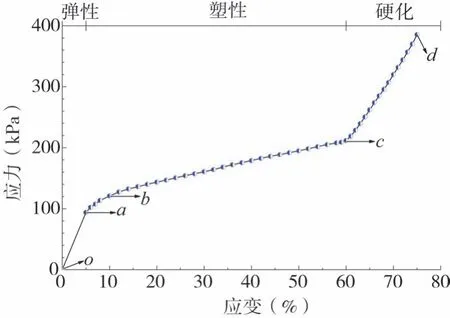
图5 EPS板应力－应变曲线Fig.5 Stress-strain curve of EPS plate

（1）将EPS的应力－应变曲线分为4条线段：oa、ab、bc和cd，每条直线的斜率表示对应应变范围内的弹性模量。各应变范围内的弹性模量见表1。

表1 各应变区间内弹性模量Table 1 Elastic modulus in each strain interval

（2）通过FLAC3D内置FISH语言中的“gp.dis.z”获得EPS顶部和底部表面的垂直位移。

（3）将EPS板顶底部之间的竖直位移差定义为EPS压缩变形Δh。Δh与EPS初始厚度（T）的比值表示该时刻EPS板的应变ε（ε=Δh/T）。

（4）根据步骤3中获得的ε确定相应的弹性模量，并将其赋予EPS板。

（5）在整个分析过程中，使用FISHCALLBACK命令重复步骤（2）～（4），连续调整EPS的力学参数，正确模拟EPS在静载及地震作用下的力学特性。

采用上述方法后，EPS的力学参数可根据其变形情况进行调整。同时，根据文献［28］提出的回归方程，将EPS板的泊松比设置为0.07。

1.2.2 其他材料参数确定

此次计算为填土和两侧边坡赋予Mohr-Coulomb本构模型，为衬砌结构和地基赋予弹塑性本构模型，模型参数源自文献［29］的研究结果，材料参数见表2。此外，由于填土、边坡以及地基之间接触，存在接触面，文中根据文献［30］的研究结果，在这些位置处设置接触面。

表2 计算模型参数Table 2 Parameters of calculation models

1.3 模型计算与动力条件输入

由于工程场地缺乏实际地震动记录，文中选取经典的Kobe波作为耦合地震动输入。根据《中国地震动参数区划图》（GB18306－2015）可确定工程场地基本地震动峰值加速度为0.3 g。一般情况下，大家普遍认为地震波竖向与水平加速度峰值之比为1/2～1/3［31］。文中竖向和水平向地震波完成滤波和基线修正后，将输入持续时间调整为20 s，竖向地震波峰值加速度调整为0.15 g，水平向峰值加速度调整为0.30 g，调整后的竖向和水平向地震波加速度时程曲线如图6和图7所示。当明洞距离震中一定距离时，竖向和水平地震波传输速度的差异必将导致二者到达明洞地基的时间存在时间差Δt［32－34］。文中根据陈育民等［23］研究，将竖向和水平地震波时间差Δt设置为2.29 s。此外，文中采用Rayleigh进行动力计算，文中根据王涛等［24］的研究，所述方法，确定体系的最小中心频率fmin为4.17 Hz，临界阻尼比ξmin取为5%。

图6 竖向地震波加速度时程曲线Fig.6 Time-history curve of vertical seismic wave acceleration

图7 水平向地震波加速度时程曲线Fig.7 Time-history curve of horizontal seismic wave acceleration

2 结果分析

2.1 地震动土压力时程曲线分析

2.1.1 洞顶竖向地震动土压力

图8为地震过程中明洞顶A－A截面中各监测点的竖向动土压力时程曲线。分析图8可知：

图8 A－A截面竖向动土压力时程曲线Fig.8 Time history curve of vertical dynamic earth pressure on section A－A

（1）从横向看，在地震持时内，A－A截面中编号为－3～3的监测点竖向动土压力时程曲线变化趋相似，竖向动土压力在0～2.29 s无明显变化，在2.29～4.4 s逐渐增大并在4.4 s时达到峰值，随后在4.4～20 s逐渐减小至某一数值并在该值附近波动；A－A截面中编号为－4和4的监测点竖向动土压力时程曲线变化趋势相反，在0～2.2 s无明显变化，2.29～4.40 s监测点－4竖向土压力逐渐减小并在4.40 s时达到最小值，而监测点4竖向逐渐增大并在4.40 s时达到最大值，4.40～20 s监测点－4和4的竖向动土压力分别减小和增大至某一数值并在该是附近波动。这是因为：0～2.29 s模型仅受竖向地震波的周期拉压作用，且该时段内作用较弱，2.29～4.4 s模型在承受周期拉压作用的同时，又开始承受水平地震波产生的剪切作用，且该时段内二者的耦合作用较强，而4.4～20 s地震波拉压和剪切耦合作用均逐渐减弱；另外，A－A截面中编号为－3～3的监测点竖向动土压力时程曲线变化趋相似，编号为－4和4的监测点竖向动土压力时程曲线变化趋势相反，这是因为编号为－3～3的监测点在EPS板底部，EPS板具有减隔震作用，在地震过程中有效减小了地震荷载对这些测点处竖向土压力的影响，而编号为－4和4的监测点分别位于土拱的左右两侧拱脚处，地震过程中，土拱一侧拱脚处土压力增大，而另一侧拱脚处土压力减小。

（2）从竖向看，在静载（即地震持时为0 s时）及地震过程中，监测点－3～3的竖向动土压力始终小于监测点－4和4的竖向土压力，这说明静载时铺设在明洞顶的EPS板促使填土中产生土拱效应，并且这一效应在整个地震过程中始终存在。此外，在地震结束后，各监测点竖向动土压力均有所增加，这是因为：地震作用使原本稳定的土体发生了较大的变形，产生了应力重分布，且这种变形可应力分布状态是不可逆的，因此就出现了这种现象。

2.1.2 明洞两侧水平地震动土压力

图9和图10分别为明洞左右两侧B－B和C－C截面中各监测点水平动土压力时程曲线，对其进行分析可知：

图9 B－B截面水平动土压力时程曲线Fig.9 Time history curve of horizontal dynamic earth pressure at section B－B

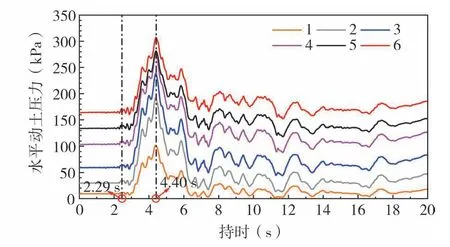
图10 C－C截面水平动土压力时程曲线Fig.10 Time history curve of horizontal dynamic earth pressure at section C－C

（1）从横向看，B－B（C－C）截面中各监测点水平动土压力时程曲线有着相似的变化趋势，水平动土压力在0～2.29 s无明显变化，在2.29～4.40 s逐渐减小（增加）并在4.40 s时达到最小（大）值，在4.40～20 s逐渐增加（减小）至某一数值后又逐渐减小（增加），产生这种变化的原因与2.1.1节中竖向动土压力的变化原因相同，此处不再赘述。此外，从图9和图10中亦可看出，在整个地震过程中，B－B截面与C－C截面中各监测点水平动土压力时程曲线变化趋势相反，呈“此消彼长”趋势。这是因为：明洞及其左右两侧填土的质量和变形能力不同，地震作用下，明洞和填土的运动速度在大小和方向上存在较大差异，导致明洞结构右侧部分与土体“挤密”，对水平土压力具有增强作用，而明洞结构左侧部分与土体“分离”，对水平土压力具有减弱作用。

（2）从竖向看，B－B（C－C）截面中各监测点水平动土压力时程曲线随着地震持时的增加先减小后增加再减小（先增加后减小再增加），各监测点水平动土压力时程曲线变化趋势相同但变化幅值不同；4.40 s时，B－B（C－C）截面中编号为－1（6）的监测点水平动土压力达到最小（大）值，为2.79 kPa（307.50 kPa），是静载水平土压力9.18 kPa（164.01 kPa）的0.28（1.87）倍。

2.2 土拱形态

2.2.1 土拱形态确定

图11为明洞顶D－D截面处竖向土压力沿填土深度的变化规律。从图11可以看出，填土总高度为H，在填土深度Ha处，竖向土压力与土柱压力完全相等，当深度小于Ha时，竖向土压力开始小于土柱压力，根据杨涛等［8］的研究，可认为P点在土拱顶部；当深度小于H1时，竖向土压力不在继续增加，开始逐渐减小，可假设土压力由增到减的拐点Q为土拱底部。设明洞顶D－D截面处P点到明洞顶的距离为Ha，Q点到明洞顶的距离为H1，因此，土拱高度为H1，土拱厚度为H2=Ha－H1。依次类推，在填土表面取一系列点xi，计算填土中过xi点竖直截面上的土拱顶部坐标（xi，Hai）和底部坐标（xi，H1i），并选择适当的曲线进行拟合，即可得到土拱顶底和底部的形态曲线，进而可以确定出具有一定厚度的土拱形态。

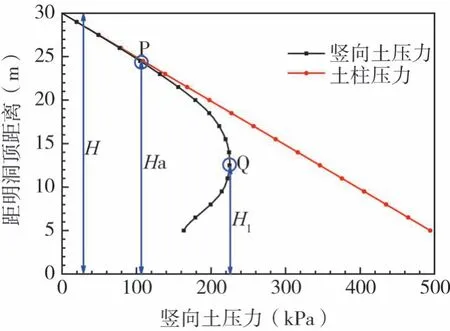
图11 土拱形态坐标确定Fig.11 Determination of soil arch coordinates

2.2.2 土拱形态变化

为了更直观的显示土拱，文中将土拱形态用红色虚线绘制在竖向土压力云图上。按照2.2.1节中所述方式确定出静载和地震持时为4.40 s时的土拱形态，如图12和图13所示。

图12 静载土拱形态Fig.12 Soil arch under static load

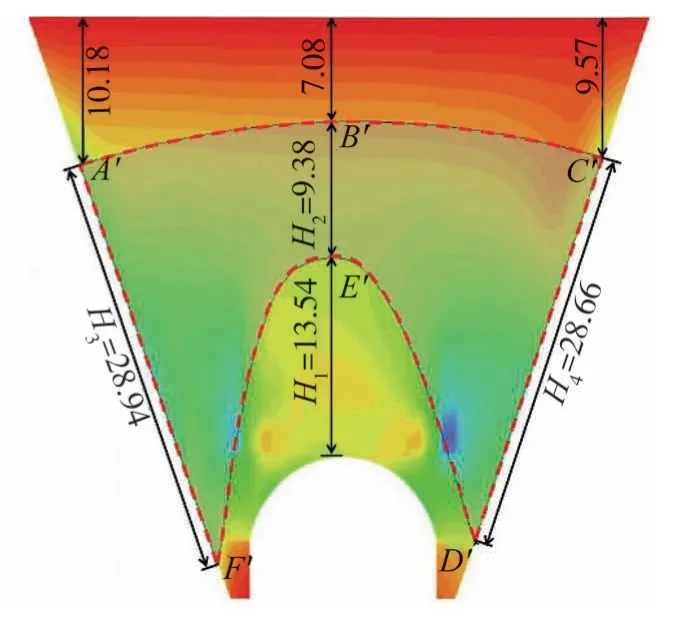
图13 地震作用下土拱形态Fig.13 Soil arch under seismic load

分析图12可知：静载条件下的土拱形态呈对称分布，土拱顶部ABC较为平缓，土拱顶部点B距填土表面5.62 m，土拱顶部与左右两侧边坡的交界点A、C距填土表面6.50 m；土拱底部DEF上凸明显，土拱底部点E到明洞顶的距离H1=12.89 m，明洞顶部的土拱厚度H2=11.49 m，两侧边坡处的土拱厚度H3=H4=32.36 m。上述分析表明，明洞顶部的土拱厚度最小，随着距明洞中央距离的增加，土拱厚度逐渐增加，并在边坡位置处达到最大值。

分析图13可知：地震持时为4.40 s时，土拱向左侧倾斜，土拱底部点E′到明洞顶的距离H1=13.54 m，增加了5.04%，土拱厚度H2=9.38 m，减少了18.36%，左右两侧土拱厚度H3和H4分别为28.94 m和28.66 m，分别减少了10.56%和11.43%。上述分析表明，地震过程中，静载时基于EPS板减载所形成的土拱依旧存在，土拱顶部A′B′C′下降，土拱底部D′E′F′升高，土拱厚度减小，土拱形态不再对称。

2.3 衬砌结构内力强度分析

图14（a）、（b）分别为静载下衬砌结构不同位置处的弯矩和轴力。由图14（a）可知：静载作用下，拱顶、拱肩和仰拱部分内侧受拉，拱顶处弯矩最大，为547 kN·m，其余位置外侧受拉，边墙顶部弯矩最大，为978 kN·m；由图14（b）可知，静载下，衬砌结构仰拱部分内侧受拉，仰拱中部轴力最大，为654 kN，衬砌结构其余各位置均处于受压状态，边墙底部轴力最大，为2 851 kN，拱顶轴力最小，为1 042 kN。上述分析表明：静载作用下衬砌结构的重点抗弯设防部位是拱顶以及左右两侧边墙顶部，重点抗拉设防部位是仰拱中部，重点抗压设防部位是左右两侧边墙底部。

图14 静载下内力分布图Fig.14 Internal force distribution under static load

为进一步明确地震过程中衬砌结构内力的变化，文中提取地震过程中衬砌结构不同位置处的峰值弯矩和轴力，如图15（a）、（b）所示。由图15（a）可知，地震作用下，弯矩不再对称分布，仰拱右侧、仰拱中部、左侧边墙下部、拱顶、右侧拱肩、右侧拱腰和右侧边墙顶部均为内侧受拉，左侧边墙底部弯矩最大，为3 733 kN·m，仰拱左侧、左侧边墙上部、左拱腰、左拱肩和右侧边墙下部均为外侧受拉，右侧边墙底部弯矩最大，为4 769 kN·m。由图15（b）可知，地震作用下，衬砌结构仰拱中部和仰拱左侧处于受拉状态，仰拱左侧轴力最大，为5 839 kN，其余各位置均处于受压状态，左侧边墙顶部和右侧边墙底部轴力较大，分别为3 259 kN和3 945 kN。上述分析表明：地震作用下衬砌结构的重点抗弯设防部位是衬砌结构左右两侧边墙底部，重点抗拉设防部位是仰拱中部和仰拱左侧，重点抗压设防部位是左侧边墙顶部和右侧边墙底部。

图15 地震作用下内力峰值分布图Fig.15 Distribution of peak internal force under seismic load

2.4 内力放大系数

静载和地震作用下，拱顶、左右两侧边墙顶部和底部是衬砌结构的重点设防部位，这些位置的内力显得尤为重要。因此，为了进一步明确地震过程中这些位置的峰值内力，文中定义了弯矩放大系数αM和轴力放大系数βN，见式（2）及式（3）。

式中：αM、βN为弯矩、轴力放大系数Mmax、Nmax为地震作用下最大弯矩、最大轴力；M0、N0为静载作用下弯矩、轴力。

由表3可知，地震作用下，拱顶、左右两侧边墙顶部、仰拱左右两侧和仰拱中部弯矩放大系数较小，而左右两侧边墙底部弯矩放大系数分别高达15.30和19.55，拱顶和左右两侧边墙顶底部轴力放大系数较小，仰拱部分轴力放大系数较大，仰拱左侧轴力放大系数最大，为22.54，这是因为：（1）静载作用下，明洞顶铺设EPS板所激发的土拱将明洞上方的土压力转移到了明洞两侧和边坡位置处，而且衬砌结构与两侧边坡之间空间狭小，土体无法沿着边坡向下沉积，明洞侧墙附近的土压力较小，作用到结构上的土压力亦较小，这导致衬砌结构左右两侧边墙的弯矩以及仰拱处的弯矩和轴力较小；（2）地震作用下，衬砌结构与左右两侧边坡和地基相互挤压，且地震作用削弱了原本基于减载产生的土拱，使填土中土压力产生重分布，作用到结构上的土压力增加，进而导致结构的弯矩和轴力增加。上述分析表明：地震作用下，衬砌结构仰拱处的轴力放大系数和左右两侧边墙底部的弯矩放大系数较大，明洞进行抗震设计时，应该对衬砌结构仰拱位置的抗拉能力和左右两侧边墙底部的抗弯能力给予关注。

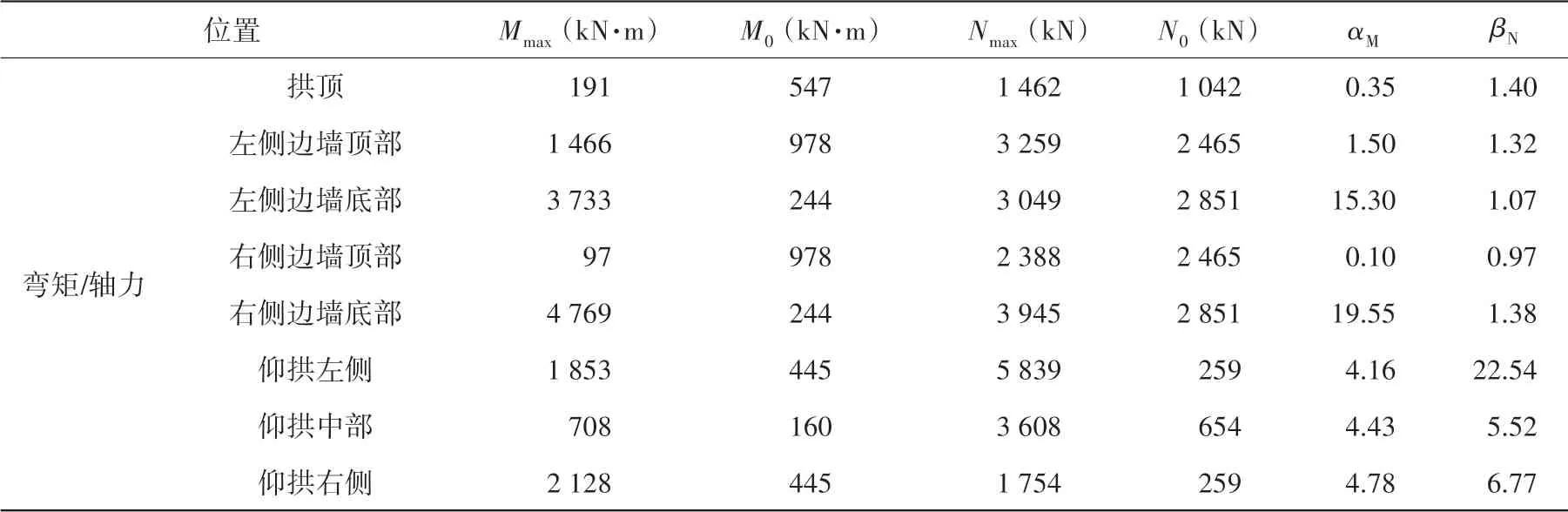
表3 监测点内力放大系数Table 3 Magnification of internal force at monitoring point

3 结论

文中采用FLAC3D数值模拟手段，对地震作用下回填土中土拱形态的演变及其引起的衬砌结构动力响应进行研究，主要结论如下：

（1）地震作用下，竖向动土压力时程曲线在距明洞中央6 m范围内变化趋势相似，在距明洞中央6～8 m范围内变化趋势相反，土压力达到峰值时，明洞顶竖向动土压力最大值为576.56 kPa，是静载作用下的1.25倍；此外，静载作用下基于EPS减载所产生的土拱在地震过程中始终存在。

（2）明洞左右两侧水平土压力时程曲线呈“此消彼长”变化，土压力达到峰值时，明洞左侧水平土压力最小值为2.79 kPa，是静载时的0.28倍，明洞右侧水平土压力最大值为307.50 kPa，是静载时的1.87倍。

（3）静载作用下，土拱形态对称分布，明洞顶土拱厚度最小，为11.49 m，两侧边坡处土拱厚度最大，为32.36 m；地震作用下，土拱形态不再对称，开始向左倾斜，土拱顶部降低，底部升高，明洞顶土拱厚度H2由11.49 m减小至9.38 m，减少了18.36%，左右两侧边坡处土拱厚度H3和H4分别由32.36 m减小至28.94 m和28.66 m，分别减小了10.56%和11.43%。

（4）地震作用下，衬砌结构左右两侧边墙底部弯矩放大系数分别高达15.30和19.55，衬砌结构仰拱左侧位置处轴力放大系数高达22.54，明洞进行抗震设计时，应该对衬砌结构仰拱位置处的抗拉能力和左右两侧边墙底部的抗弯能力给予关注。