基于分区软化拉压杆模型的矩形RC剪力墙水平承载力计算方法
张博鸿,马高,2
(1.湖南大学土木工程学院,湖南 长沙 410082;2.工程结构损伤诊断湖南省重点实验室(湖南大学),湖南 长沙 410082)
引言
在实际建筑结构中,剪力墙存在压、弯和剪共同作用,受力状态和传力机理十分复杂。一般认为剪跨比大于2的剪力墙是弯曲控制为主,而对于剪跨比不超过2的剪力墙,在荷载作用下其内部的应力及应变场呈不连续的特征,平截面假定已不再适用,很多学者对这类剪力墙的受力机理、承载能力做了研究和阐述,其中软化拉压杆模型是较具有代表性的模型之一。
软化拉压杆模型是学者黄世建教授在拉压杆模型[1]基础上发展起来的一种新模型。该模型抗剪强度的获得需编程后反复迭代计算,不易在实际工程中推广应用。为此,黄世建等[2]于2002年提出了便于设计人员手算的简化软化拉压杆模型。Sanchez-Alejandre等[3]基于该简化软化拉-压杆模型对收集的剪力墙数据库进行分析,认为轴向荷载和垂直分布筋的配筋率对剪跨比2以下剪力墙的抗剪能力起到了增强作用。Kassem[4]假定剪跨比2以下的剪力墙均为主斜压杆失效破坏,基于黄世建的简化软化拉-压杆模型和大量试验数据的拟合,给出了剪跨比2以下剪力墙的承载力计算公式。黄炜等[5]通过拟合参数有限元分析,将软化拉压杆模型推广于复合墙板,提出了相应的斜截面承载力公式。
然而黄世建抗剪承载力模型的假定为主斜压杆破坏,未考虑拉杆对承载力的影响。就破坏模式而言,这种假定仅适用于剪切破坏,认为主斜压杆发生破坏时,结构恰好达到承载力峰值,例如刘鸣等[6]、董俊宏等[7]学者将软化拉压杆模型运用于节点中,均取得了较好的效果,但根据韩小雷等[8]、Lefas等[9]的剪力墙试验可知,当在剪跨比小于1时,剪力墙易发生剪切破坏,而剪跨比1~2之间的剪力墙多是弯剪耦合破坏,这导致原软化拉-压杆模型的假定在剪力墙中不能广泛适用。在力学平衡方面,软化拉-压杆模型中顶部水平力的抵抗作用并非由斜压杆单独完成,而是依靠拉压杆机构共同完成,仅由斜压杆承载能力反算剪力墙承载力,忽略了拉杆的限制,会使拉杆控制的剪力墙计算值偏大。此外,通过观察剪力墙的裂缝特征[10-17],发现其开裂过程存在分区的情况,即受拉暗柱和腹板处于弯剪区或斜压区,而受压暗柱处于剪压区,这说明剪压区的暗柱也应额外承担水平荷载。
针对上述问题,文中在原软化拉压杆模型的基础上,提出了考虑拉杆屈服和边压杆抗剪作用的分区软化拉压杆模型计算方法,并通过剪切破坏和弯剪破坏2类试验数据与规范公式、相关学者计算模型的对比分析,验证了该计算方法的有效性。
1 矩形剪力墙数据库
1.1 数据收集
文中收集了242个矩形RC剪力墙试验数据[8-14,18-42],多为带暗柱构造,不包含混凝土强度大于80 MPa、带交叉钢筋等改进型钢筋混凝土剪力墙试验数据,加载方式大多数为低周往复加载。搜集的数据包含截面尺寸、暗柱长度、剪跨比、轴压比、混凝土强度、水平分布钢筋配筋率、竖直分布钢筋配筋率、暗柱纵筋配筋率等,其中剪跨比2以内的剪力墙190片,剪跨比2以上的剪力墙52片,剪切破坏剪力墙73片,弯剪破坏剪力墙169片。
1.2 数据统计
由图1可以看出:(1)数据库中剪力墙剪跨比在0~3之间均有分布,剪跨比小于2的占78.5%,主要为低矮剪力墙,其中剪跨比为0.5~1的剪力墙占比最大;(2)轴压比以低轴压比为主,轴压比0~0.1之间剪力墙占79.5%;(3)混凝土圆柱体抗压强度主要分布于20~40 MPa;(4)水平分布筋和竖向分布筋配筋率主要集中在0~1%之间;(5)暗柱纵筋配筋率多分布在0~6%之间。

图1 剪力墙数据库各参数频率分布Fig.1 Frequency distribution of the parameters of shear wall data base
2 软化拉压杆模型
剪力墙的软化拉压杆模型如图2所示,Vd、Vh、Vv代表各机构所承担的抗剪能力,结构总抗剪能力为各机构抗剪能力之和。

图2 剪力墙的软化拉压杆模型Fig.2 Softened strut-and-tie model of shear wall
文中先简要介绍软化拉压杆模型的简化计算方法,公式中各系数的详细推导过程参见文献[2]。模型总抗剪能力V1的计算公式为:

式中:K为拉压杆系数;ζ为开裂混凝土软化系数;f'c为混凝土圆柱体抗压强度;Astr为斜压杆有效面积;θ为斜压杆与水平方向夹角。各项具体可写为:

式中:as为斜压杆高度;bs为斜压杆宽度,取墙厚;H为剪力墙墙片高度;h为加载梁高;l为剪力墙计算长度。各项具体可写为:


式中:b为剪力墙厚;N为墙上承担的竖向荷载;Ag为剪力墙截面面积;L为剪力墙长度;la为暗柱长度,无暗柱时取0.2L。
式(1)中拉压杆系数K可以写为:

式中:Kh、Kv为水平拉杆、竖向拉杆修正系数,其作用为修正拉杆发挥程度,形式如下:

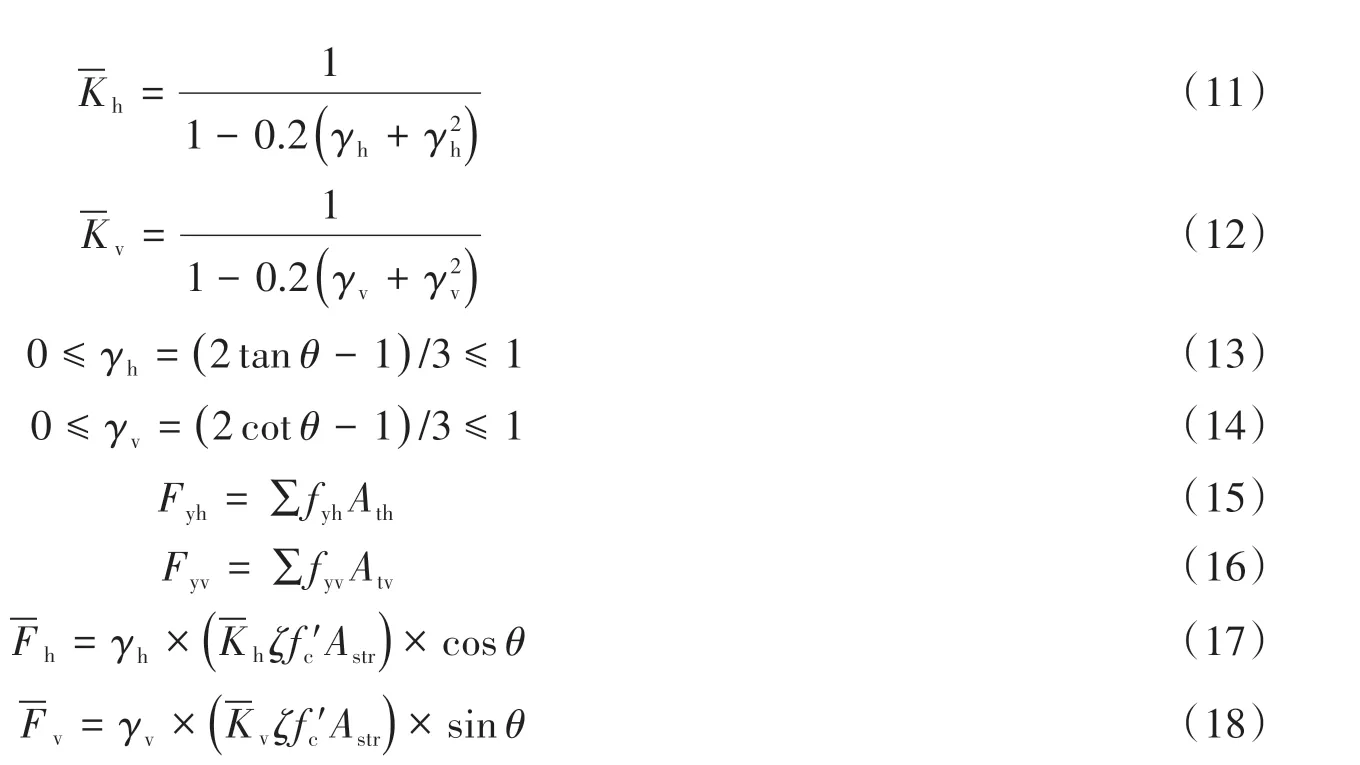
式中:γh为水平拉杆与节点水平剪力的比值;γv为竖向拉杆与节点竖向剪力的比值;fyh、fyv为水平钢筋、竖向钢筋的屈服强度;Ath为水平钢筋截面面积,取墙高0.25~0.75H范围内全部水平分布钢筋面积以及该范围外水平分布钢筋面积的一半[1],以考虑水平筋的实际贡献;Atv为全部竖向分布筋截面面积。
3 分区软化拉压杆模型
3.1 剪力墙受力机理分析
基于剪力墙弯剪破坏的试验现象[10-11](图3(a)所示),依据其裂缝的发展规律及受力状态的特点,可分为弯剪、剪压2个区域,即:受拉暗柱及腹板处于弯剪区,其裂缝属于弯剪裂缝,数量较多,越接近剪压区,裂缝受压力影响越大,裂缝越偏于陡峭,一般发展至受压暗柱内侧边缘;受压暗柱则处于剪压区,其在承载力峰值时,承受较大压力,裂缝数量不多。
而对于发生脆性剪切破坏的剪力墙[12-14](图3(b)所示),可分为斜压、剪压2个区域,即:受拉暗柱及腹板处于斜压区,其裂缝属于典型通长斜裂缝,数量较多,其通长主斜裂缝近似对角发展,受压暗柱依然处于剪压区,其在承载力峰值时,会出现若干斜裂缝,此斜裂缝较主通长裂缝更陡峭。以上特征表明剪力墙存在2个分区且工作机理存在差异。

图3 剪力墙受力分区图及分区模型Fig.3 Force partition diagram of shear wall and partition model
对于受拉暗柱和腹板而言,受拉暗柱区域出现较为水平的裂缝,表明纵筋受拉力;腹板出现斜裂缝,表明腹板受拉、压共同作用。当斜压杆破坏而拉杆未屈服时,结构会呈现脆性剪切破坏,形成斜压区;而当拉杆先屈服时,桁架承载力将由拉杆控制,产生弯曲裂缝,后因结构变形导致斜压杆强度软化而最终发生主斜压杆破坏或暗柱角部破坏时,结构会呈现弯剪破坏,形成弯剪区。对于受剪切和压力共同作用的受压暗柱(边压杆),其受力机理与传统抗剪原理相似,为水平筋屈服和暗柱混凝土在剪力和压力的复合作用下,主拉应力超过其抗拉强度而破坏或在高轴力下被压碎。2个分区贡献的叠加即为剪力墙总水平承载力。最终的剪力墙分区软化模型如图3(c)所示,该模型中当边拉杆屈服先于主斜压杆破坏时,对应图3(a)的弯剪破坏,当主斜压杆破坏先于边拉杆屈服时,对应图3(b)的剪切破坏。
3.2 分区软化拉压杆模型计算概念
受拉暗柱和腹板抗水平力贡献符合软化桁架模型,但原软化模型未考虑拉杆对桁架水平承载力的限制作用,故需要补充软化桁架在拉杆控制下的水平承载力计算概念,具体表述为:总剪力按原软化拉压杆模型给出的分配比例式(19)~式(21)分配至各机构(如图2所示),当水平和竖向机构均不屈服时,分配比例见式(20)~式(21),若某一机构先屈服,剩余机构分配比例按式(19)计算[2],水平和竖向机构均屈服后,水平力仅由斜向机构承担。当边拉杆屈服时,若竖向机构的中拉杆未屈服,则剪力墙承载力可继续增长至中拉杆屈服,但在此过程中需考虑边压杆受压抗力的限制,若在中拉杆屈服前,边压杆角部所受竖向力超过其受压抗力,则边压杆破坏,中拉杆无法完全屈服。
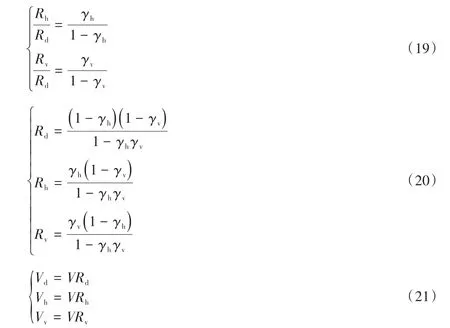
基于上述拉杆控制下的剪力墙承载能力计算概念,再结合原软化拉压杆的斜压杆控制计算概念,两者计算结果取小值,便可求得剪力墙受拉暗柱和腹板区域的实际抗剪承载力贡献。除此之外,作为边压杆的受压暗柱区域会为结构提供额外的水平承载力,其贡献可按剪压概念求解。两个分区贡献的叠加即为剪力墙总水平承载力。
3.3 分区模型组成部分定义
如图3可知,考虑各分区上方所受实际竖向荷载的影响,将式(5)和式(7)修改为式(22)和式(23),其中la为暗柱长度,无暗柱剪力墙的暗柱长取0.2L,L为剪力墙长度。

计算剪跨比取剪力墙高和加载梁高的一半与计算模型长度的比值:

边拉杆抗力取暗柱内的纵筋屈服力和暗柱上方分配的竖向荷载之和,其中Aaz为暗柱纵筋面积:

中拉杆抗力取全部竖向分布筋屈服力和腹板上方分配的竖向荷载之和,Atv为全部竖向分布筋面积:

水平机构中水平拉杆抗力由水平分布筋屈服力构成:

压杆角部受压抗力按下式计算,Aa为暗柱面积:

3.4 边拉杆贡献计算
由图2桁架模型可知,虽然水平或中拉杆屈服会导致其对应的机构屈服,从而使机构间分配比例发生变化,但机构各自顶部所承担水平力与边拉杆最大受力部分的比值总是等于计算剪跨比,因此无论机构间内力如何分配,各机构边拉杆受力总和与承担水平力总和的比值也总等于计算剪跨比。故边拉杆的抵抗水平力贡献不受机构间分配比例的影响,其值为:

3.5 中拉杆额外贡献计算
在计算边拉杆贡献时,其中竖向机构所分配的剪力不足以让中拉杆屈服的情况下,结构可通过继续变形使中拉杆继续受力,此时新增长的中拉杆受力,文中定义为中拉杆额外抗力,记为Fzle。
当各机构均不屈服时,竖向机构的边拉杆受力为FblRv,其中竖向机构的边拉杆与中拉杆受力相等,所以当FblRv≥Fzl时,中拉杆屈服,故不能提供额外抗力;仍在FblRv≥Fzl条件下,当由于水平拉杆配置不足,导致水平机构先屈服时,会使竖向机构承担到比原来(FblRv)更大的力,此时中拉杆也会屈服无额外贡献。故有式(30),其中Fzle为中拉杆额外抗力:

当FblRv<Fzl时,中拉杆额外贡献将受水平机构的影响,当水平机构不屈服时,可先求出水平机构的边拉杆受力FblRh,然后剩余边拉杆抗力中竖向机构的边拉杆受力可按(Fbl-FblRh)γv计算,若(Fbl-FblRh)γv>Fzl,则说明中拉杆屈服,此时中拉杆无额外抗力,故中拉杆额外抗力有如式(31):
FblRv 在FblRv<Fzl的情况下,若水平机构屈服,则水平机构的受力将由水平拉杆抗力控制,根据水平机构桁架模型中水平拉杆与边拉杆受力关系可知,此时水平机构边拉杆受力为Fslλ′,同上可求得此时中拉杆额外抗力为: 除此之外,还需考虑边压杆角部受压抗力对中拉杆额外抗力发挥程度的限制,即压杆角部受压抗力要大于等于压杆本身所受竖向荷载、边拉杆贡献计算时通过机构传递来的竖向压力、中拉杆额外贡献计算时传递过来的竖向压力之和,故压杆角部受压抗力限制下中拉杆额外可发挥抗力为: 最后Fzle1、Fzle2、Fzle3三者取小值,并根据几何关系可由中拉杆额外抗力求得中拉杆额外抵抗水平力贡献。 根据上述推导可知,腹板纵筋可与混凝土斜压杆组成桁架机构抵抗水平力,但其受力较为复杂,腹板纵筋贡献受到模型的分配比例、暗柱纵筋抗力、水平分布筋抗力、竖向分布筋抗力、轴力、剪跨比及受压暗柱角部受压抗力的影响。其中,随着剪跨比的降低,竖向机构分配比例逐渐增大,弯剪区受剪切影响逐渐增加,其抵抗水平力的贡献会受到抑制。 边压杆由受压暗柱构成,其主要受剪力和压力的复合作用,可按传统剪压原理去考虑,即边压杆的抗剪贡献可分为混凝土贡献Vcb和钢筋贡献Vsb。 受压暗柱混凝土贡献Vcb,根据材料力学理论可按式(36)求得[43], 式中:b为墙厚。边压杆钢筋贡献Vsb仍采用45o桁架模型来计算,计算长度取暗柱长度可得式(37), 式中,ρh为水平分布筋配筋率。则边压杆抗剪承载力贡献可表示为: 根据上文可知拉杆控制的剪力墙受拉暗柱和腹板区域水平承载力公式可表示为: 结合原软化拉压杆方法,剪力墙受拉暗柱和腹板区域最终水平承载力贡献可表示为: 叠加受压暗柱区域边压杆抗剪贡献的剪力墙水平承载力公式可表示为: 为测试公式的适用范围,将全部剪力墙(共242片)代入公式进行验证,效果如图4(a)所示。可观察到试验值比计算值(Vtest/Vcal)的平均值、变异系数和平均误差均较好,但剪跨比大于2的数据平均值偏低,这说明对于中剪跨比的剪力墙,文中计算方法计算值偏大,这是由于暗柱混凝土贡献均按最大值叠加计算造成的。根据试验现象[10-14],在承载力峰值时中剪跨比剪力墙较低剪跨比剪力墙受压暗柱区域完整度更高,说明随着剪跨比的增大,受压暗柱抗剪贡献的发挥程度在降低。为考虑剪力墙剪跨比的影响,同时保持公式中系数的简洁,文中以混凝土贡献比上计算剪跨比进行修正,并考虑到修正后的混凝土贡献不得大于理论上混凝土所能提供的最大抗剪承载力值,故有式(42)。修正后的公式预测效果如图4(b)所示,可观察到预测值随剪跨比的变化平稳。 图4 文中模型水平承载力预测结果Fig.4 Horizontal bearing capacity prediction results based on the current model 文中将低剪跨比剪力墙数据库分为剪切破坏(I类,73片)和弯剪破坏(Ⅱ类,169片)2类,并选取了7个具有代表性的规范及相关学者提出的剪力墙抗剪承载力公式进行分类对比分析。表达式中的符号已与前文进行了统一,前文未提及的变量均在下方进行了注释。将2类数据库中各试件参数分别代入文中公式与文献公式,计算试验值比计算值的平均值与变异系数,如图5和表1所示。对于规范公式,亦采用材料的实测强度值代入进行计算。图5中的剪跨比按λ=(H+0.5h)/L计算。文献公式简要介绍如下: 图5 规范及文献水平承载力预测结果Fig.5 Horizontal bearing capacity prediction results based on codes and literature (1)中国规范JGJ 3-2010[44] 式中:λ0取(H+0.5h)/h0,其中H为墙高,h0取L-0.5la,L为墙长,h为加载梁高,λ0小于1.5时,取1.5,大于2.2时,取2.2;N为轴力,大于0.2fctL时,取0.2fctL,t为墙厚;sv为水平分布钢筋的竖向间距;βc为混凝土强度影响系数,当fcu不超过C50时,βc取1.0,当fcu大于C80时,βc取0.8,其间按线性内插法确定;Ash为配置在同一截面内的水平分布筋的全部截面面积。 (2)美国规范ACI 318-19[45] 式中:αc为混凝土强度对墙抗剪强度的贡献系数,当λ小于1.5时,取0.249,当λ大于2.0时,取0.166,其间按线性内插法确定;ρh为全部水平钢筋截面面积与水平钢筋垂直剪力墙面的面积之比;fyh为水平分布筋屈服强度。 (3)新西兰规范NZS 3101:2006[46] 式中:vc1、vc2为混凝土抗剪强度,vc1取0.27f'0.5c+N/(4Ag),vc2取0.05f'0.5c+L(0.1f'0.5c+0.2N/Ag)/(M/V-L/2),当M/VL/2≤0时,只取vc1;d为有效墙长,取0.8L。 (4)日本规范AIJ-99[47] 式中:v为混凝土有效抗压强度系数,取0.7-f'c/200;tanθ0取[(H0/l)2+1]0.5-H0/l;β为桁架机制中混凝土斜压杆的压应力与混凝土有效强度之比,取(1+cot2ξ)ρhfyh/(vf'c);H0为加载点至墙底垂直距离;l为计算长度取L-la;fyh为水平分布筋屈服强度,超过400 MPa时取400 MPa,当ρhfyh大于vf'c/2时,取vf'c/2;ξ为桁架机构中混凝土斜压杆倾角,对于墙cotξ取1。 (5)Hwang模型[2] 模型公式和含义参见前文。 (6)Sánchez-Alejandre模型[3] 式中:γ取0.42-0.08λ;ηv取0.75+0.05ρvfyv;ηh取1-0.16ρhfyh≥0.2;ρv为竖向分布钢筋截面面积与竖向钢筋垂直剪力墙面的面积之比;ρh为全部水平钢筋截面面积与水平钢筋垂直剪力墙面的面积之比;fyh为水平分布筋屈服强度;fyv为竖向分布筋屈服强度。 (7)Kassem模型[4] 式中:Ψ取0.95-f'c/250;ks取as/dw;dw取do-as/3;α取tan-1(Hw/dw);ωh取ρhfyh/f'c;ωv取ρvfyv/f'c;d0为纵向受拉钢筋合力到受压边缘距离,取L-0.5la;Hw为加载点到底梁距离;ρv此处为竖向分布钢筋截面面积与剪力墙厚度和dw乘积的比值。 由图5和表1可知中国规范JGJ 3-2010模型在计算I类数据库时的Vtest/Vcal整体偏高(1.419),且随着剪跨比的降低平均值明显增大,说明其设计公式较为保守,特别是在低剪跨比范围,此外规范计算结果的变异系数也较大(0.384);美国规范ACI 318-19在计算I类数据库时Vtest/Vcal的变异系数(0.281)比中国规范稍好,但也偏于保守(平均值为1.365),同时也存在随剪跨比的降低计算值越来越保守的问题;新西兰规范在计算I类数据库时的统计参数与中国美国规范类似;日本规范的计算原理是基于桁架模型和拱模型,其在计算I类数据库时Vtest/Vcal的平均值较为准确(1.032),但变异系数较大(0.418);对于Sánchez-Alejandre模型,在计算I类数据库时,模型的预测值较为保守,但变异系数较小(0.238);Kassem模型在计算I类数据库时,结果整体上较为准确(Vtest/Vcal平均值为1.088),变异系数也较小(0.222);Hwang模型在计算I类数据库时,计算结果的变异系数(0.206)较好但平均值较为保守(1.177),在计算Ⅱ类数据库时,由于未考虑拉杆控制导致计算值整体偏不安全(平均值0.768),文中模型在计算I类和Ⅱ类数据库时,计算结果的变异系数均最小(0.170和0.136)、平均值均较为准确(1.033和1.027),又由图4(b)可知模型预测结果随剪跨比的变化稳定,说明该计算模型能合理反映剪力墙受力机理随剪跨比的变化情况。 表1 水平承载力Vtest/Vcal的统计参数Table 1 Statistical parameters of horizontal bearing capacity Vtest/Vcal 对比上述规范与文献模型的计算结果可知,对于Ⅰ类数据库,各国规范计算公式(除日本规范),整体较为保守,变异系数均较大,而学者提出的抗剪公式相比规范在在平均值和变异系数上均有改善,但目前的抗剪公式均无法在Ⅱ类数据库中适用,这是因为弯剪破坏的剪力墙既受到弯的影响又受到剪的影响,需要考虑弯剪耦合。对于文中模型,基于Hwang的模型考虑了弯剪分区后,在Ⅰ类数据库和Ⅱ类数据库中Vtest/Vcal的平均值和变异系数相对于原模型得到了明显改善,且该模型基于力学推导,对于剪切和弯剪均适用。因此文中提出的改进软化拉压杆方法较为合理,可为剪力墙剪切和弯剪模型的相关研究提供参考。此外,文中模型表达式较简洁、物理意义明确,可为实际工程提供指导。除根据公式可对剪力墙配筋等相关参数进行设计外,还可从拉杆与压杆的受力关系出发,设计拉杆先于压杆屈服,使剪力墙在地震下的破坏形式为延性破坏,避免非延性破坏。 (1)剪力墙抵抗水平力的工作机制存在分区行为,受拉暗柱和腹板处于弯剪区或斜压区,其弯剪机制符合软化桁架模型;受压暗柱处于剪压区,其抗剪机制符合混凝土构件剪压原理。其中剪切破坏可通过模型的斜压区叠加剪压区表达,弯剪破坏可通过模型的弯剪区叠加剪压区表达。 (2)文中所提出的考虑拉杆屈服及边压杆抗剪的分区软化拉压杆模型,在剪切破坏和弯剪破坏两类数据中的变异系数对比规范和文献其它方法均有显著降低,平均值也更准确,且文中基于力学推导的分区模型在各剪跨比区间计算结果的平均值均较为稳定,说明文中模型适用范围较广,能合理反映剪力墙的工作机理。此外,该方法不需要迭代,计算过程简便,适用于实际工程应用。 (3)建议在剪力墙设计时,通过增大混凝土强度等方式,使文中所提剪切破坏公式中的V1大于弯剪破坏公式V2,即让剪力墙中拉杆屈服先于主斜压杆破坏,从而使低矮剪力墙避免纯剪切破坏。同时可通过调节弯剪公式V2中水平和竖向分布筋的配筋量进行合理配筋,避免配筋过少时剪力墙承载力过低发生剪切破坏或配筋过多时出现无效配筋而造成浪费。 (4)文中模型破坏机理按裂缝划分,模型适用于剪跨比3以下的以斜向裂缝为主的剪切破坏矩形RC剪力墙和水平裂缝与斜向裂缝并存的弯剪破坏矩形RC剪力墙,但对于剪跨比大于3剪力墙的适用性,需要进一步研究。



3.6 边压杆贡献计算



3.7 方法验证及分析





4 模型比较与分析



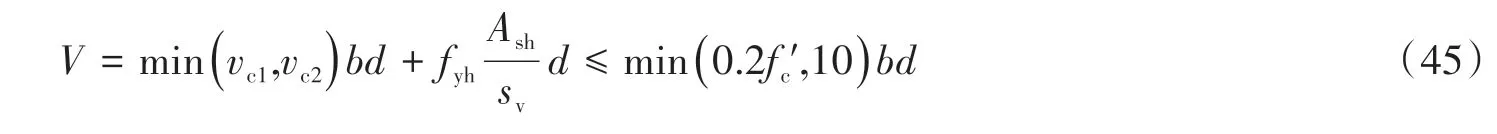
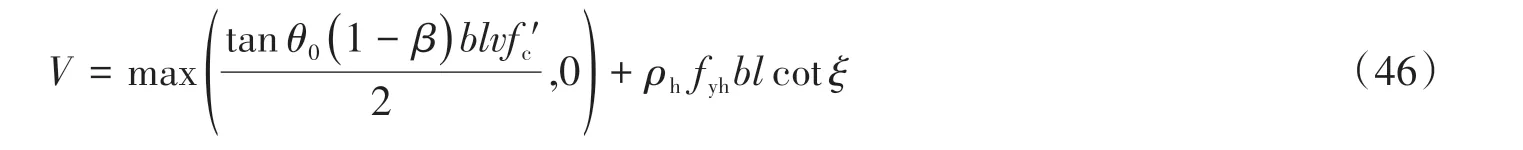



5 结论

