静止无功发生器对双馈风电场高频振荡的影响

吴林林，程浩，刘京波，杜东冶，龚超，郭春义

(1. 华北电力科学研究院有限责任公司（国网冀北电力有限公司电力科学研究院），北京 100045；2. 新能源电力系统国家重点实验室（华北电力大学），北京 102206)

0 引言

在碳达峰·碳中和的背景下，以风电为代表的新能源大规模接入电网，使得中国电网正逐渐演变为“双高”电力系统[1-3]。静止无功发生器(static var generator, SVG)具有无功补偿迅速且灵活等优势，能够有效解决风电机组出力不确定性导致的母线电压波动问题，可提高风电场并网系统的电压稳定性，在风电场中得到了广泛应用[4-6]。然而，SVG的接入可能会影响风电场在高频段的稳定性，例如，2021年5月，中国某含SVG的双馈风电场出现了2 500 Hz左右的高频振荡现象，风电场母线电压波形严重畸变，导致风电场中多台SVG闭锁，给风电场的安全稳定运行带来了严峻的挑战。

针对含SVG风电场的稳定性问题，已有学者进行了诸多研究。文献[7-9]建立了含SVG的风电场阻抗模型和状态空间模型，分析了风电场中次同步振荡的产生机理及其影响因素；文献[10]建立了考虑SVG和并网母线处并联电容器的阻抗模型，探究了风电场中频振荡的产生机理。以上文献重点研究了SVG与风电场内其他设备的交互作用对风电场稳定性的影响，然而研究频段却集中在较低频段。

针对风电场中出现的高频稳定性问题，文献[11]分析了电网在并联电容补偿、串联电容补偿和无补偿3种无功补偿方式下，与风电场之间的高频振荡产生机理，并提出在风电变流器内环附加有源阻尼环节重塑风机阻抗的高频振荡抑制方法；文献[12-14]建立了包含电缆线路的直驱风电场和双馈风电场阻抗模型，分析了风电场高频振荡的影响因素，研究结果表明：电缆长度是影响风电场高频振荡特性的主要因素；文献[15-18]指出风电机群与模块化多电平换流器(modular multilevel convert，MMC)之间、风机与风机之间相互作用，同样存在高频振荡风险。以上研究重点分析了风电场的高频振荡现象，然而均未考虑SVG的接入。目前SVG被广泛应用于风电场并网系统，但其对风电场高频振荡的影响尚不明确，亟须进一步研究。

为此，本文以国内某含SVG的双馈风电场为研究对象，建立包含双馈风电机群、集电线路和SVG的高频阻抗模型，同时，在 PSCAD/EMTDC中搭建包含4条风电机群链路、集电线路与SVG的双馈风电场仿真模型，通过阻抗扫描与理论阻抗对比，验证所建立的双馈风电场高频阻抗模型的准确性；基于所建立的风电场高频阻抗模型，分析双馈风电场的高频振荡现象，探究SVG系统参数对双馈风电场高频振荡特性的影响；最后，在所建立的仿真模型中验证忽略风电机组间架空线的可行性以及理论分析的正确性。

1 双馈风电场高频阻抗建模

1.1 双馈风电场拓扑结构

本文以中国某双馈风电场为研究对象，其并网系统如图1所示，4条链路双馈风电机组经机端变压器升压，经电缆线路接入35 kV母线，每条链路由15台参数相同的双馈风机和1条电缆线路组成，风电场并网点（point of common coupling,PCC）点处安装有SVG。为方便后续研究，本文将SVG定义为SVG子系统；将所有风电机组、电缆和交流电网组成的系统看作一个整体，定义为剩余子系统。

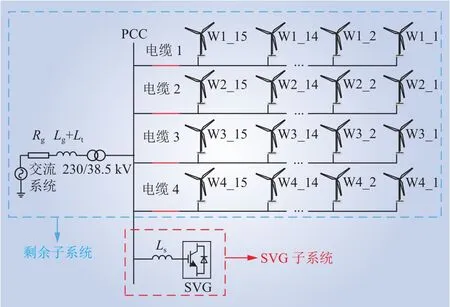
图1 风电场拓扑Fig. 1 Wind farm topology

1.2 剩余子系统高频阻抗建模

单台双馈风机拓扑结构如图2所示，主要由双馈绕线式异步发电机、转子侧变流器、网侧变流器、LC滤波器和机端变压器组成，单台风机电网侧阻抗ZG和转子侧阻抗ZR[13]分别为

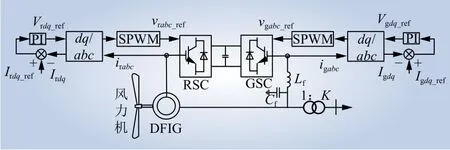
图2 双馈风机拓扑结构Fig. 2 Topology of doubly-fed wind turbine

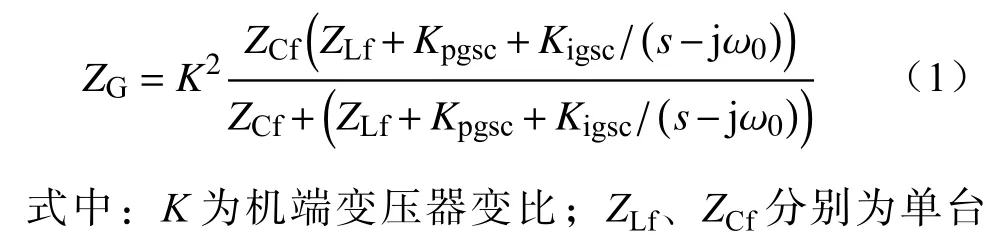
为了模拟电缆线路的阻抗特性，本文采用级联π型等值电路，电缆的π型等值电路如图3所示，π型等值电路参数计算公式为

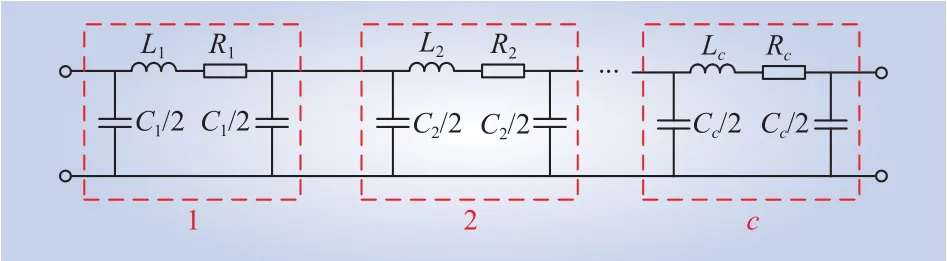
图3 电缆线路π型等值电路Fig. 3 Cable line π-type equivalent circuit

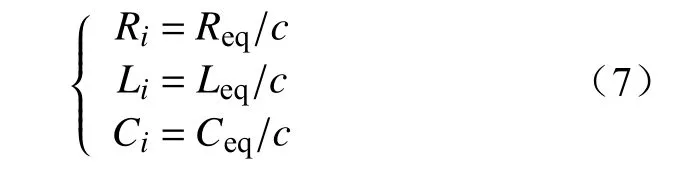
式中：Ri、Li、Ci分别为第i个π型等值单元的参数；c为π型电路单元的个数。

1.3 SVG子系统高频阻抗建模

采用双闭环控制的SVG结构如图4所示，图中：uabc、iabc分别为PCC点三相电压、电流；uref_abc为SVG输出电压参考值；Udc为直流侧电容电压；Ls为SVG机端滤波电感。

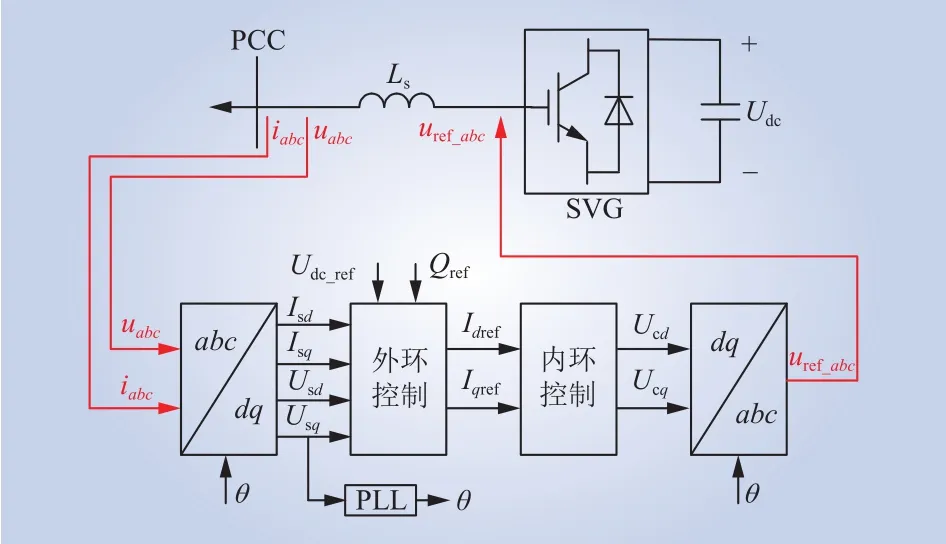
图4 SVG拓扑及控制示意Fig. 4 SVG topology and control

SVG变流器控制系统中锁相环和外环对其高频阻抗特性的影响较小[23-24]，因此建立SVG的高频阻抗模型时，可以忽略锁相环和外环的影响，得到 SVG的降阶阻抗模型，如图5所示[24-25]。

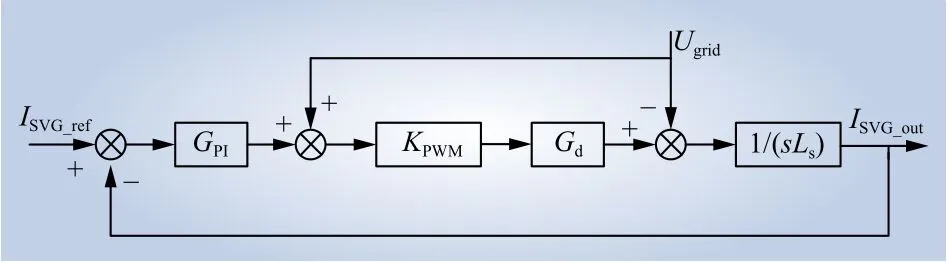
图5 SVG降阶阻抗模型Fig. 5 SVG reduced-order impedance model

图5中：ISVG_ref为内环电流参考值；ISVG_out为SVG输出电流；Ls为SVG机端滤波电感；KPWM为调制参数，这里将KPWM等效为1；GPI为内环PI 控制器的传递函数；Gd为包含电压、电流采样延时和PWM调制延时在内的系统总延时环节，计算公式为

式中：Td为系统总延时。

根据传递函数的输入输出关系，由图5可推导出SVG高频阻抗ZSVG为

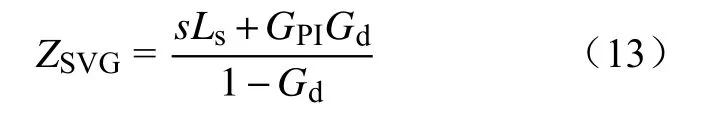
1.4 高频阻抗模型验证

为了减少仿真计算量，提高仿真速度，根据1.2节所述的风机等值方式，在搭建风电场电磁暂态仿真模型时对4条链路做了相应简化，即将每条链路中15台参数相同的2 MW风机（单台2 M W风机参数如表1所示）等值为单台30 MW风机，最终在 PSCAD/EMTDC中搭建的电磁暂态仿真模型拓扑结构如图6所示，具体参数参考国内某风电场的部分实际运行参数，如表2所示。考虑到当前实际风电场高频振荡的频率范围在1～3 kHz之间，故本文研究的频段为1～3 kHz。

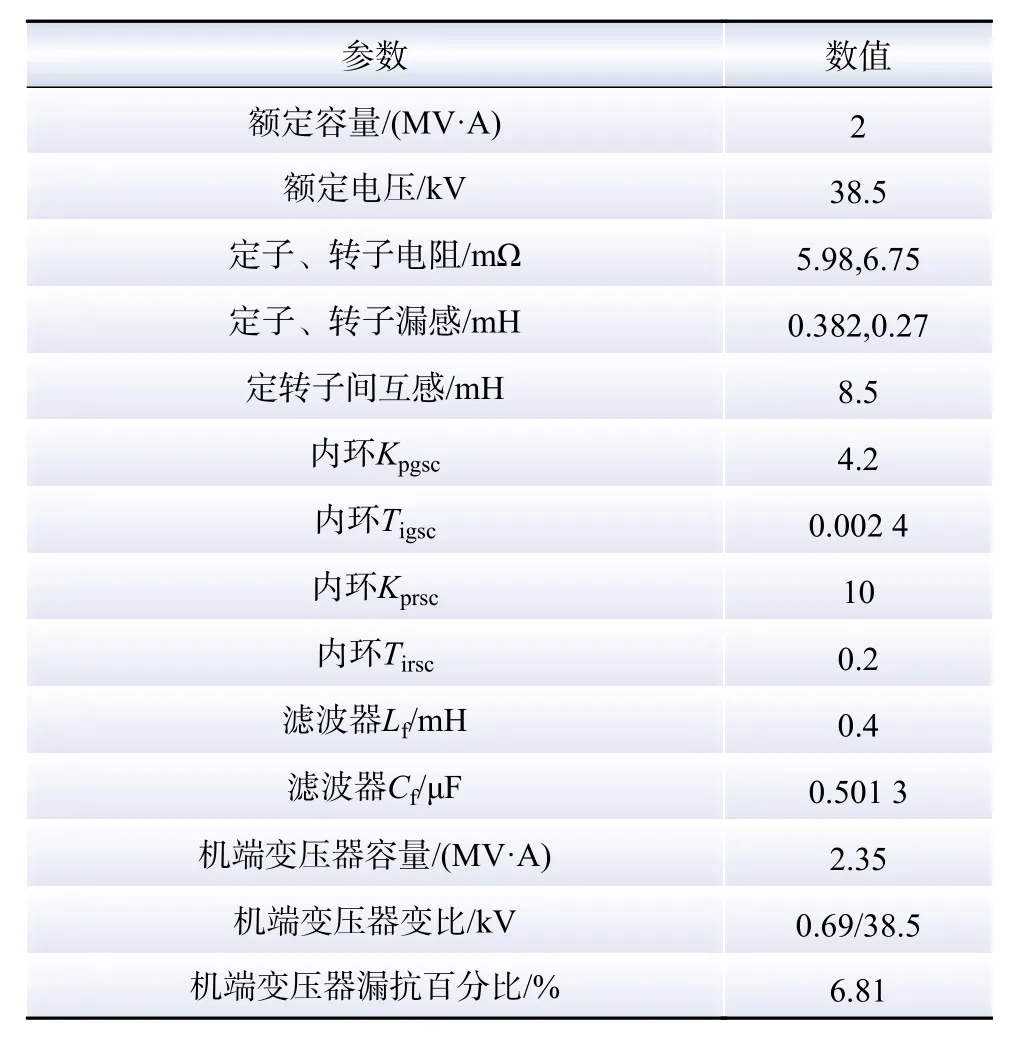
表1 2 MW双馈风电机组参数Table 1 Parameters of 2 MW doubly-fed wind turbine

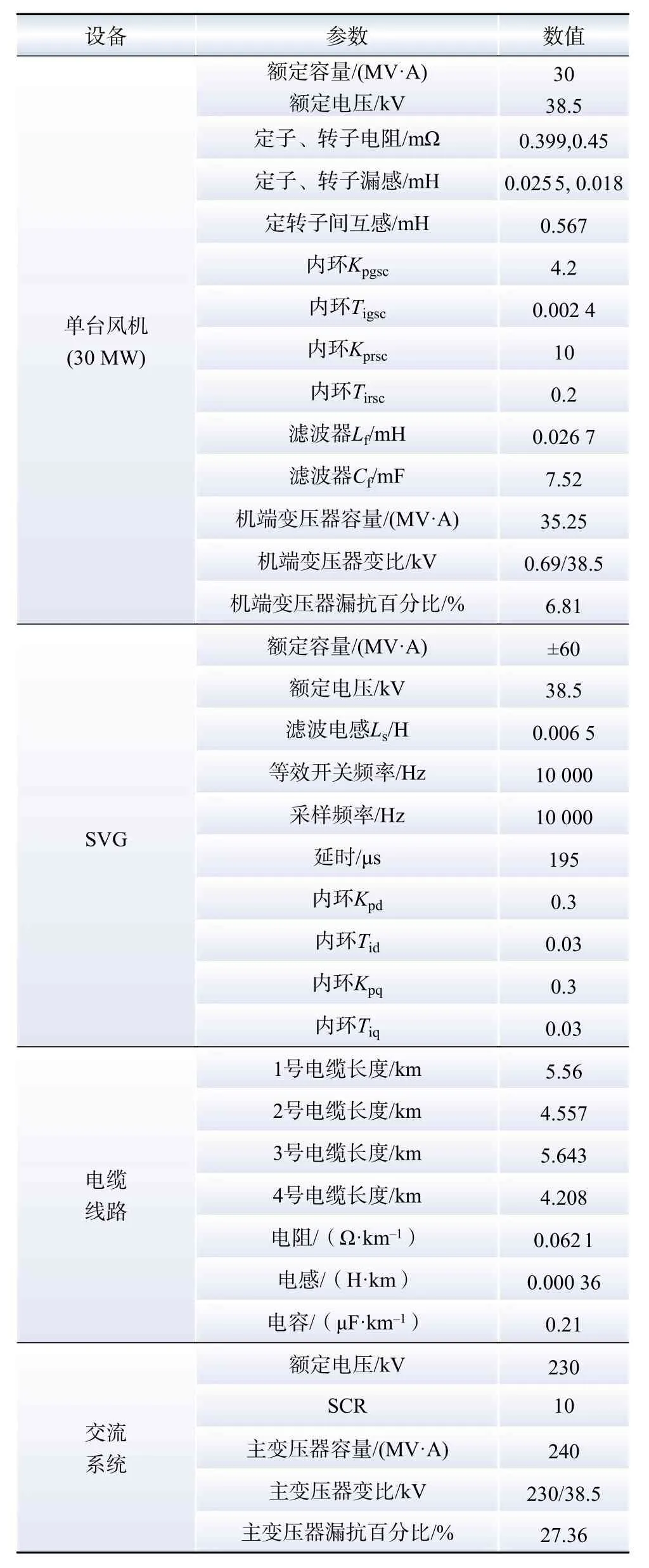
表2 国内某双馈风电场主要参数Table 2 Main parameters of a domestic doubly-fed wind farm

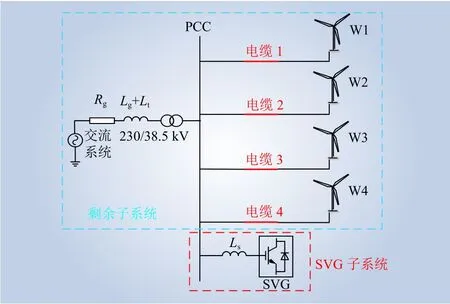
图6 等值后风电场拓扑结构Fig. 6 Equivalent wind farm topology

剩余子系统和SVG子系统的理论计算阻抗和扫频阻抗对比结果如图7、8所示。其中理论计算阻抗是基于第1节所建高频阻抗模型计算得到，扫频阻抗是基于在PSCAD/EMTDC中所建考虑锁相环和外环的全阶仿真模型得到。由图7～8可知，2个子系统的理论计算阻抗曲线与扫频阻抗曲线高度吻合，验证了所建高频阻抗模型的准确性。

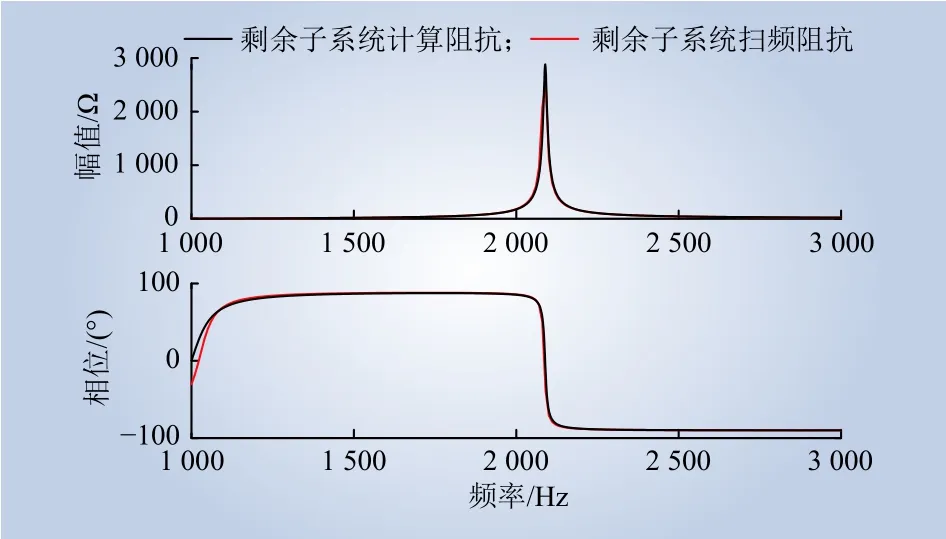
图7 剩余子系统计算阻抗和扫频阻抗Fig. 7 Calculated impedance and sweep impedance of remaining subsystem

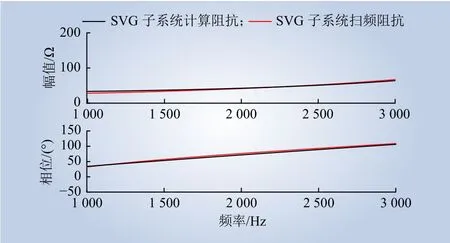
图8 SVG子系统计算阻抗和扫频阻抗Fig. 8 Calculated impedance and sweep impedance of SVG subsystem

进一步地，根据高频阻抗模型来分析双馈风电场的高频振荡现象，2个子系统的理论阻抗对比结果如图9所示。由图9可知，2个互联子系统阻抗曲线幅值交点横坐标为2 452 Hz，对应的相位差为180.4°，根据阻抗稳定性判据[26-27]可知，当延时为195 μs时，SVG子系统与剩余子系统在频率为2 452 Hz处相位裕度不足，存在发生高频振荡的风险。

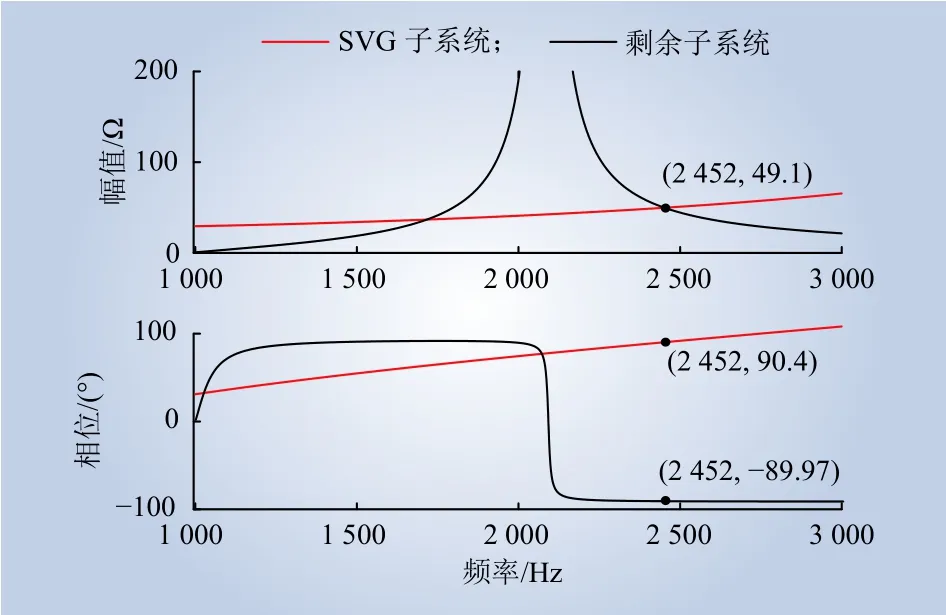
图9 2个子系统计算阻抗和扫频阻抗对比Fig. 9 Calculated impedance and sweep impedance of of two subsystems

2 SVG对风电场高频振荡的影响

2.1 SVG延时的影响

为了说明SVG延时对风电场高频振荡特性影响的普遍性，本文选取3个案例作为研究对象。

案例1：风电场中的电缆长度如表2所示，SVG 延时分别取 185 μs、195 μs和 205 μs时，2 个互联子系统计算阻抗对比结果如图10所示。

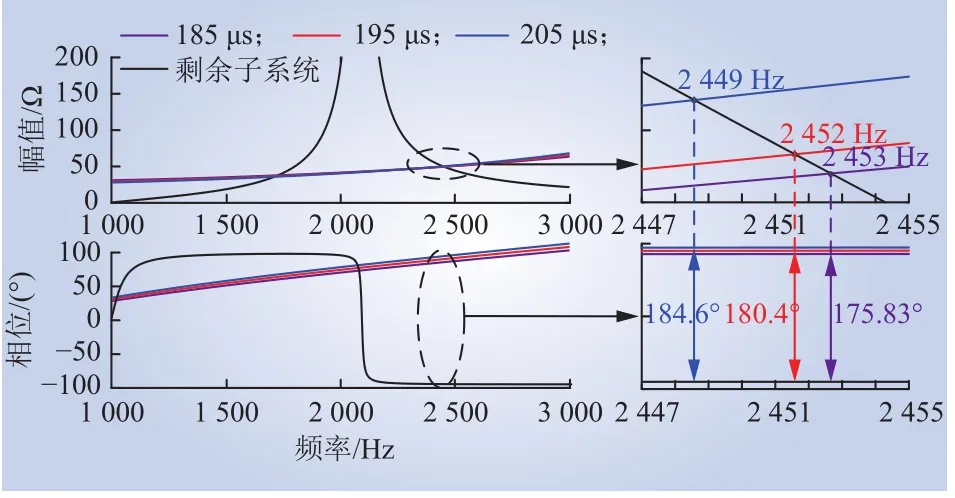
图10 案例1中2个互联子系统计算阻抗对比Fig. 10 Calculated impedance of two interconnected subsystems in case 1

案例2：保持系统其他参数不变，风电场每条链路中的电缆长度与案例1中相比均减少0.75 km，SVG 延时分别取 175 μs、185 μs和 195 μs时，2 个互联子系统计算阻抗对比结果如图11所示。

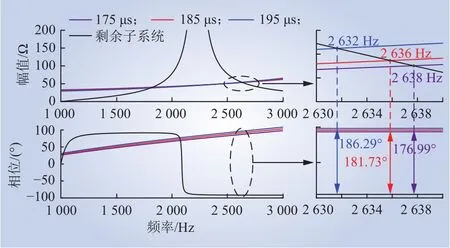
图11 案例2中2个互联子系统计算阻抗对比Fig. 11 Calculated impedance of two interconnected subsystems in case 2

案例3：保持系统其他参数不变，风电场每条链路中的电缆长度与案例1中相比均增加0.75 km，SVG 延时分别取 195 μs、205 μs 和 215 μs时，2 个互联子系统计算阻抗对比结果如图12所示。

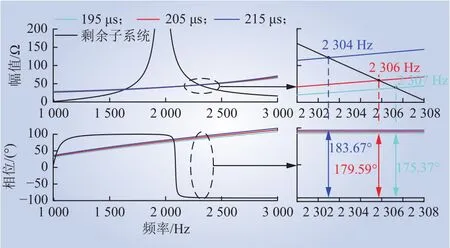
图12 案例3中2个互联子系统计算阻抗对比Fig. 12 Calculated impedance of two interconnected subsystems in case 3

由图10～12可知，在每个案例中，当电缆线路长度相同，而SVG延时大小在一定范围内变化时，2个互联系统的阻抗幅值曲线交点的位置几乎没有变化；随着SVG延时的增大，阻抗曲线幅值交点处对应的相位差在不断增大，系统的相位裕度逐渐变小，系统发生高频振荡的风险逐渐升高。

对比图10～12，在不同案例中，当延时相同，而线路长度变化时（以延时td=195 μs为例），随着4条电缆长度增加，2个互联系统阻抗幅值曲线交点的位置向低频段移动，对应的相位差逐渐减小，系统发生高频振荡的风险逐渐降低。

2.2 SVG滤波电感的影响

保持系统其他参数不变，SVG滤波电感分别为5.85 mH、6.50 mH和7.15 mH时，2个互联子系统阻抗特性曲线的对比结果如图13所示。由图可知，随着SVG滤波电感的增大，2个互联子系统阻抗幅值曲线的交点向低频段移动，阻抗曲线交点处对应的相位差逐渐减小，系统发生高频振荡的风险随SVG滤波电感增大而逐渐降低。

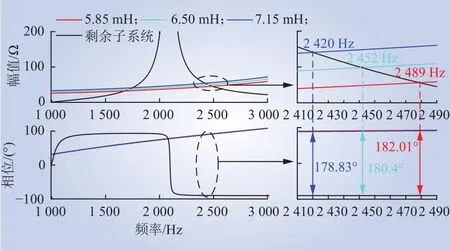
图13 滤波电感不同时2个互联子系统计算阻抗对比Fig. 13 Calculated impedance of two interconnected subsystems with different filter inductances

2.3 SVG控制参数的影响

保持系统其他参数不变，SVG内环比例系数Kp分别为0.1、0.3、1.0时，2个互联子系统阻抗特性曲线的对比结果如图14 a)所示，SVG内环积分时间常数Ti分别为0.001、0.03、0.1时，2个互联子系统阻抗特性曲线的对比结果如图14 b)所示。由图14可知，随着SVG内环比例系数Kp的增大，系统发生高频振荡的风险逐渐升高；SVG内环积分时间常数Ti在一定范围内变化时，对系统高频振荡特性没有影响。

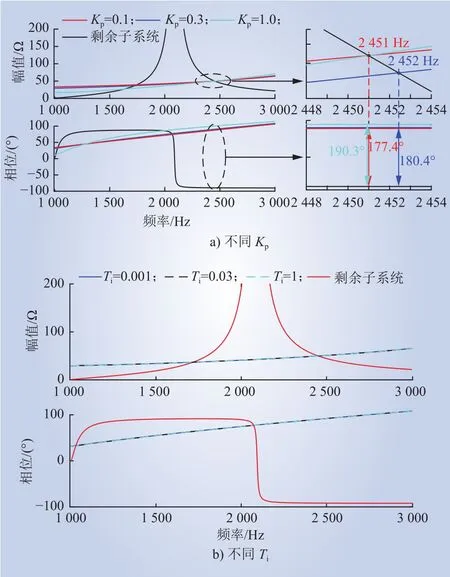
图14 SVG不同控制参数下2个子系统计算阻抗对比Fig. 14 Calculated impedance of two subsystems under different control parameters of SVG

2.1～2.3节针对SVG参数对风电场高频振荡特性的影响仅做了定性分析，为了体现各参数对风电场高频振荡特性影响的大小，将2.1～2.3节理论分析结果量化汇总，如表3所示。

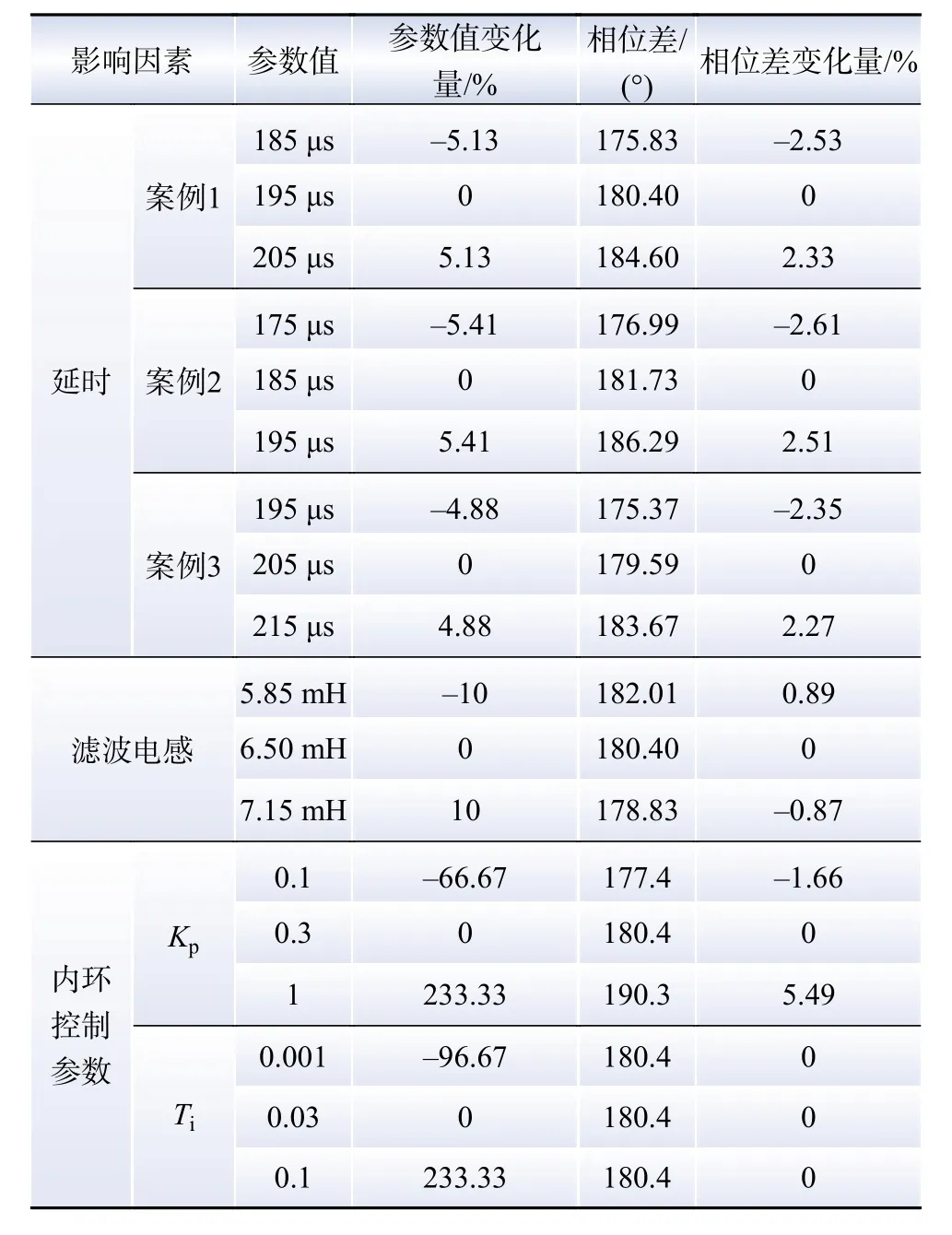
表3 SVG参数对高频稳定性的影响Table 3 Influence of SVG parameters on high frequency stability

对于表3中的各个影响因素，均以中间行的参数值和对应相位差的大小为基值(变化量为0，通过改变参数值的大小，观察该参数和对应相位差的变化量的大小，来判断该参数对风电场高频振荡特性影响的大小，即若某参数变化量越小，相位差变化量越大，则该参数对风电场高频振荡特性的影响越大。例如，案例1以延时为195 μs、相位差为180.4°时的工况为基准，当延时大小增加或减少5.13%时，其相位差增加2.33%或减少2.53%。

由表3可知，SVG延时、滤波电感和内环比例系数均会影响系统的高频振荡特性；此外，对比各种工况下的参数变化量和对应的相位差变化量可知，SVG延时变化量最小时，对应的相位差变化量最大，可见SVG延时是影响风电场高频振荡特性的主要因素。

3 仿真验证

3.1 忽略机组间架空线的合理性验证

前2节的分析均是基于忽略风电机组间架空线的等值风电场模型进行的，因此，本节首先通过仿真来验证建立高频阻抗模型时忽略风电机组间架空线的合理性。

为此，基于表1、表2和表4所示各设备参数，在PSCAD/EMTDC中分别建立了如图15所示的详细仿真模型和图6所示的等值仿真模型，二者的区别仅在于链路1是否考虑了风电机组间的架空线，阻抗扫描结果对比如图16所示。当SVG延时为175 μs，2个系统均处于稳定状态，将2个系统的延时由175 μs切换到195 μs，此时详细仿真模型和等值仿真模型的PCC点三相电压波形及A相电压FFT分析结果分别如图17和图18所示。

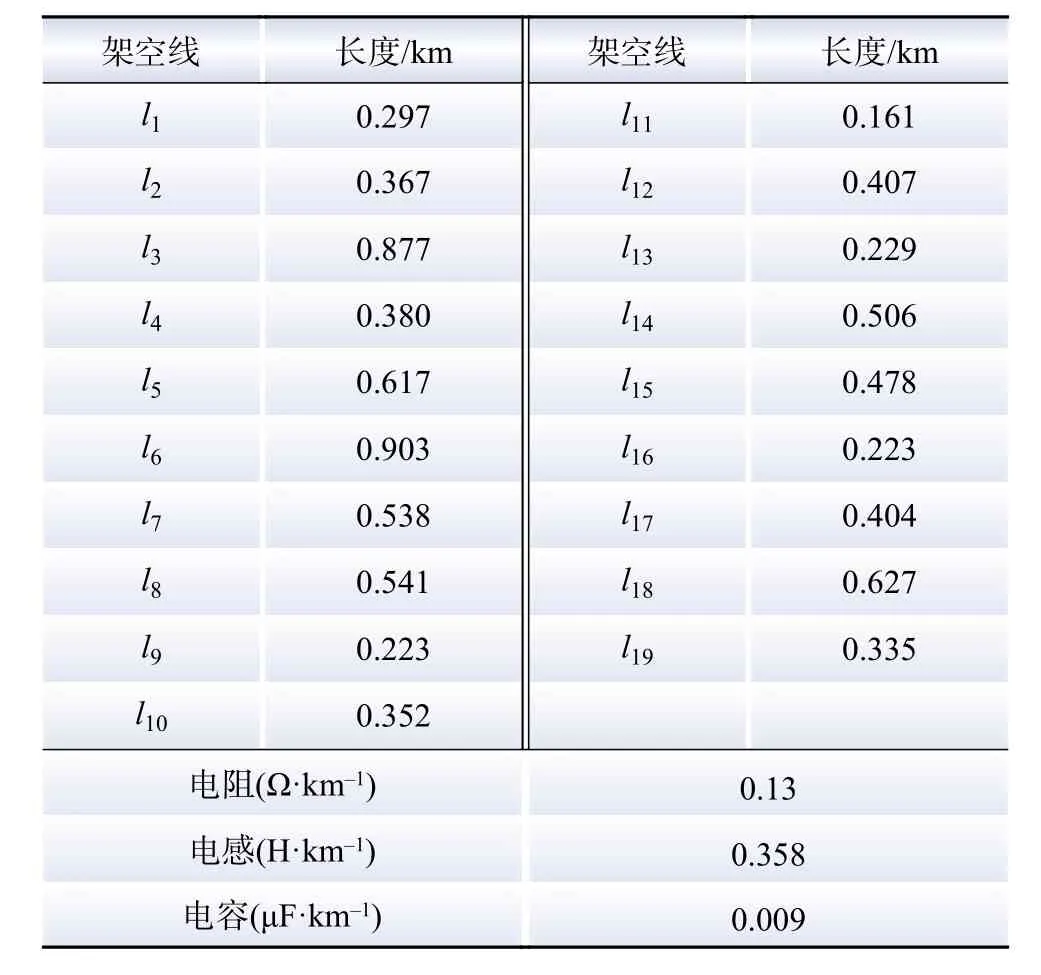
表4 链路1风电机组间架空线参数Table 4 Parameters of overhead lines between wind turbines in link 1

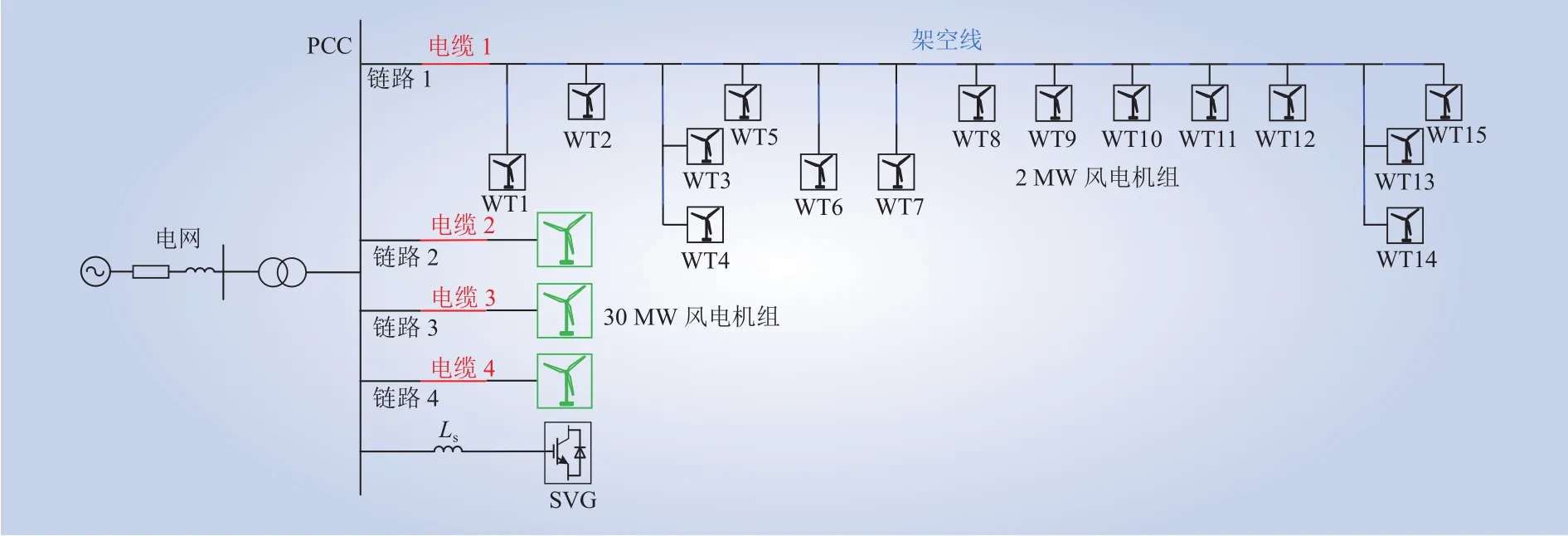
图15 详细仿真模型拓扑结构Fig. 15 Detailed simulation model topology

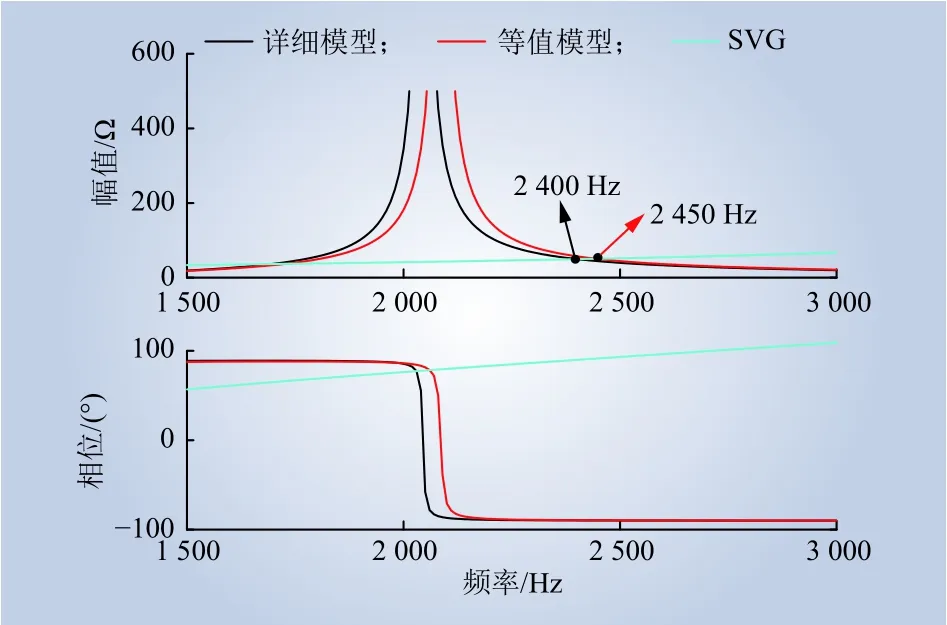
图16 详细模型与等值模型阻抗扫描结果对比Fig. 16 Impedance scan results of detailed model and equivalent model

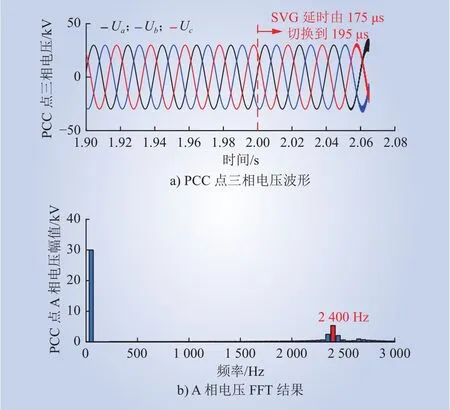
图17 详细模型PCC点三相电压波形及A相电压FFT结果Fig. 17 Three-phase voltage waveform of detailed model PPC point and results of A-phase voltage FFT

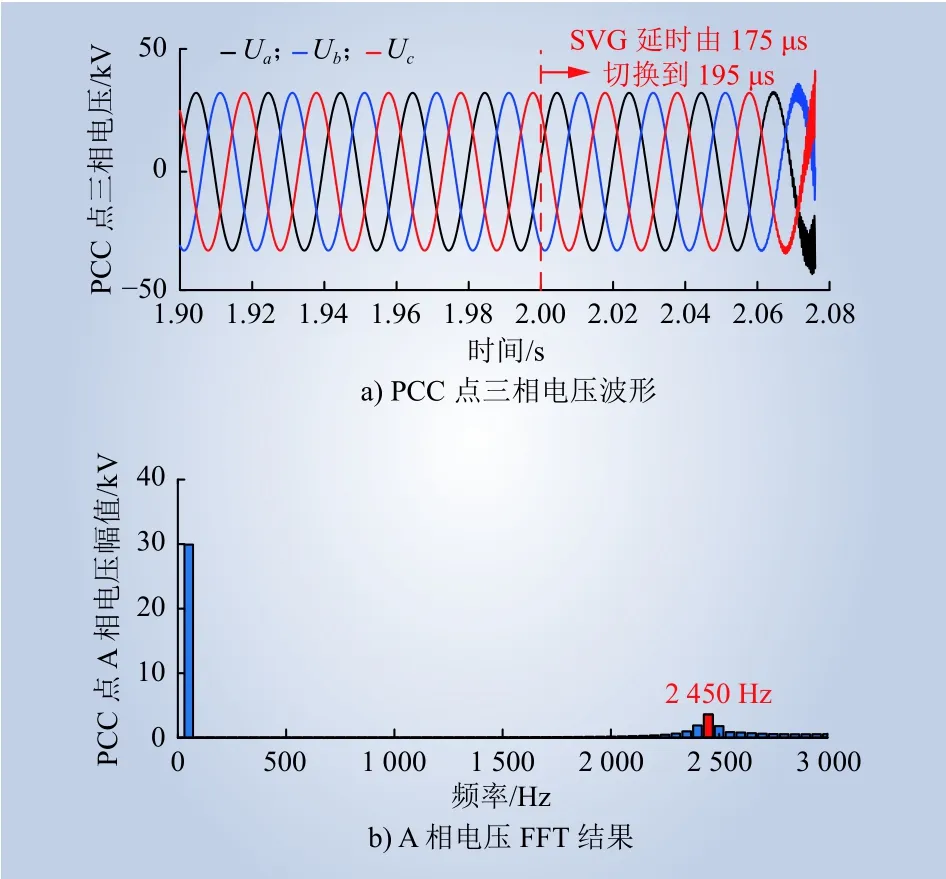
图18 等值模型PCC点三相电压波形及A相电压FFT结果Fig. 18 Three-phase voltage waveform of equivalent model PCC point and results of A-phase voltage FFT

由图16～18可知，2个仿真模型发生高频振荡时的振荡频率分别为2 400 Hz和2 450 Hz，以详细模型为基准，频率误差为2%，高频振荡现象基本一致，且二者的阻抗扫描结果除在谐振峰附近差50 Hz左右外，阻抗特性基本一致，因此，忽略机组间的架空线对风电场高频振荡的影响较小，在进行高频阻抗建模时忽略风电机组间的架空线是合理的。

3.2 SVG参数对高频振荡特性的影响

由上一节的理论分析知，SVG延时、滤波电感和内环比例系数均会影响风电场的高频振荡特性，但考虑到实际工程中切换滤波电感的可行性较低，故针对SVG延时和SVG内环比例系数Kp，通过2个仿真案例来验证理论分析的正确性。

案例1：保持其他参数不变，在t=2 s时将SVG 延时由 175 μs切换到 195 μs，此时 2 个互联系统所对应的理论计算阻抗曲线如图19所示。

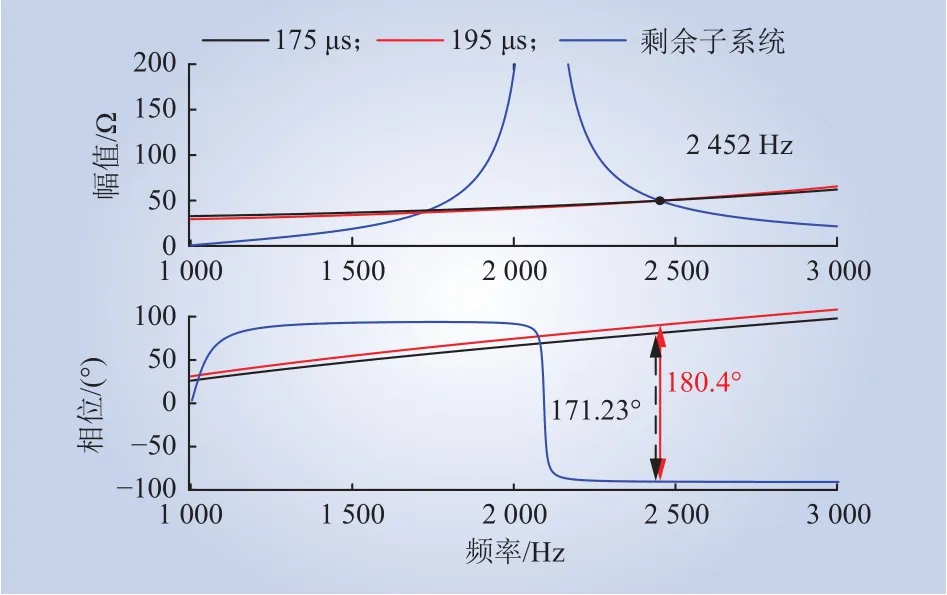
图19 SVG子系统与剩余子系统计算阻抗对比（案例1）Fig. 19 Calculated impedance between SVG subsystem and remaining subsystems (case1)

由图18可知，延时由175 μs切换到195 μs后，系统发生了高频振荡，振荡频率主要集中在2 450 Hz附近；而图19中对案例1的理论分析结果表明，当延时由175 μs切换到195 μs后，2个互联系统计算阻抗幅值在2 452 Hz处存在交点，该频率下相位差为180.4°，根据阻抗分析法，此时系统发生高频振荡。由此可见，案例1的仿真结果与理论分析结果基本一致。此外，案例1也表明，当SVG延时增大时，2个互联系统的阻抗曲线幅值交点处对应的相位差将增大，系统的相位裕度将变小，导致系统发生高频振荡的风险增加，这与 2.1 节理论分析所得的结论是吻合的。

案例2：保持其他参数不变，在t=5.2 s时将Kp由0.3切换到0.5，在t=5.3 s时将Kp由0.5切换到1，系统PCC点三相电压波形如图20所示；此时2个互联系统所对应的理论计算阻抗曲线如图21所示。

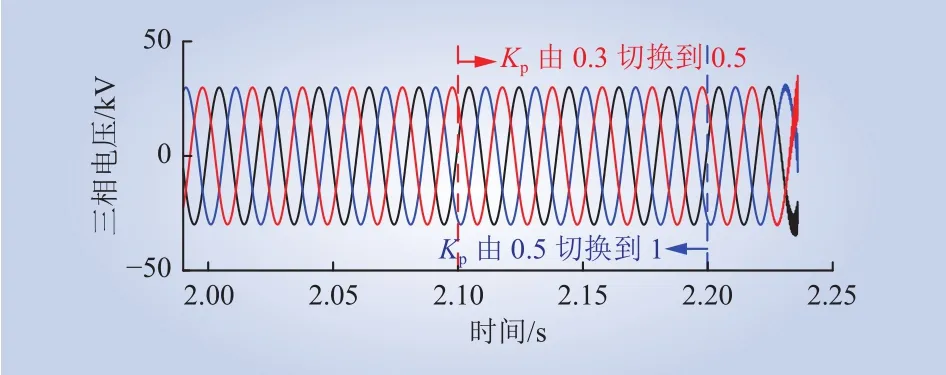
图20 PCC点三相电压波形Fig. 20 Three-phase voltage waveform at PCC point

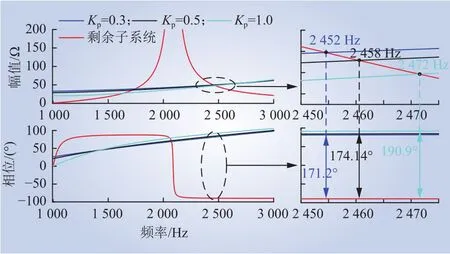
图21 SVG子系统与剩余子系统计算阻抗对比（案例2）Fig. 21 Calculated impedance between SVG subsystem and remaining subsystems (case2)

由图20可知，SVG内环比例系数Kp从0.3切换为0.5时，系统保持在稳定状态，接着从0.5切换为1.0后系统发生高频振荡；而图21中对案例2的理论分析结果表明，当内环比例系数Kp从0.3增大到0.5时，对应的相位差从171.2°增大到174.14°，根据阻抗分析分析法，此时系统稳定，而当内环比例系数Kp从0.5增大到1.0时，对应的相位差从174.14°增大到190.9°，根据阻抗分析法，此时系统发生高频振荡。由此可见，案例2的仿真结果与理论分析结果基本一致。此外，案例2也表明当SVG内环比例系数Kp增大时，2个互联系统的阻抗曲线幅值交点处对应的相位差在不断增大，系统的相位裕度逐渐变小，同样会增加系统发生高频振荡的风险，这与2.3节理论分析所得的结论是一致的。

4 结论

本文首先建立了包含SVG的双馈风电场高频阻抗模型，并进行了高频阻抗模型验证，然后根据理论高频阻抗模型分析了双馈风电场的高频振荡现象；在此基础上，从理论和仿真2个角度分析了SVG延时、滤波电感、内环控制参数对双馈风电场高频振荡特性的影响，得出结论如下。

（1）SVG电压前馈延时、滤波电感和内环比例系数均会影响风电场的高频振荡特性，其中SVG电压前馈延时是影响风电场高频振荡特性的主要因素；（2）SVG电压前馈延时在一定范围内变化时，基本不影响2个互联子系统阻抗曲线交点的位置，但延时增大会使阻抗曲线交点处相位差增大，从而增加双馈风电场发生高频振荡的风险；（3）随着SVG滤波电感的增大，2个互联子系统阻抗幅值曲线的交点会向低频段移动，同时阻抗曲线交点处相位差逐渐减小，双馈风电场发生高频振荡的风险逐渐降低；（4）SVG内环积分时间常数在一定范围内变化对风电场高频振荡特性没有影响，但内环比例系数增大时会导致双馈风电场发生高频振荡的风险升高。