基于群体共识算法的深度学习推荐系统评价

李楚贞，吴新玲，余育文

1.广东理工学院 信息技术学院，广东 肇庆 526100

2.广东技术师范大学 计算机科学学院，广州 510665

3.广州工商学院 工学院，广东 佛山 528131

4.肇庆学院 校长办公室，广东 肇庆 526100

深度学习和推荐系统是近年来迅速发展的两大新兴算法，将两者融合能够在预测用户的未来偏好方面更为迅速和准确，并且能够解决由于复杂社会网络信息的复杂性和实时更新造成的信息过载问题。深度学习推荐系统现广泛应用于语音识别、图像处理、用户偏好预测、购物平台精准推荐、疫情防控以及自然语言处理等领域[1-2]。深度学习推荐系统管理中的重要问题之一是深度学习推荐系统的评价与优选，而其本质上是一个群决策问题。群决策（group decision making，GDM）需要基于群共识来筛选最佳方案，并能够提高决策者（decision maker，DM）对方案的满意度。在群决策过程中，DM通常借助模糊判断矩阵（fuzzy judgment matrix，FJM）来表达对备选方案进行两两对比后的评价信息。因此，面向FJM 的共识调整模型是GDM 领域中最值得研究的问题之一[3-5]。

GDM中共识调整模型的一个重要问题是设计有效的调整策略。DM 不仅关注运用共识调整模型进行调整后的FJM是否满足共识阈值，而且希望尽可能少地调整DM的初始意见。因此，文献[6]提出了最小调整成本的思想，以获得一个可接受的最小调整共识解决方案，并成为近年来的热门话题[7-10]。文献[7]研究了基于区间2型模糊环境中共识实现过程的多准则群决策方法，并以中国四支新上市股票的最优投资组合比率计算为例验证了方法的有效性。文献[8-9]探讨了最小调整共识模型的原始-对偶共识模型及其经济意义。在有限的共识成本预算下，文献[10-11]建立了最大专家共识水平的模型。文献[12]在分布式偏好群决策问题中首次尝试在共识调整过程中引入专家可靠性，并建立了一种基于动态专家可靠性的群体共识达成模型，进而通过对江苏常州某高端装备制造企业供应商选择问题验证了方法的适用性和有效性。文献[13]引入了一种新的基于限制等价函数的犹豫模糊语言内聚性度量方法以推动大多数人的共识过程，从而降低了共识调整过程中内部分歧的影响。Cheng等[14]将最小调整共识模型扩展到不对称成本环境中，其中DMs 在提高和降低决策观点时的单位成本不相等。Labella 等[15]使用一致性度量构建了具有FJM 的最小调整共识模型。Zhang 和Pedrycz[16]提出了两阶段优化模型解决具有GDM中的个体一致性和群体一致性问题。Wu等[17]设计了多阶段优化模型以实现调整成本、修改偏好值的数量和需要进行调整的DM数量最小化。

然而，现有的研究大多建立静态的共识调整模型来优化所有决策者的调整偏好值，很少考虑到不同DM的调整参数通常不一致的问题。因此，有必要针对共识水平低的DM提出一种基于优化的调整策略，以便在GDM中运用最优调整参数达成最小调整成本共识。于是，本文引入衡量FJM 一致性和FJM 之间共识水平的指数公式，然后设计了基于最小调整成本的共识调整反馈机制以获得最优调整参数，使得所有不一致的DM满足最低调整成本的一致性阈值，最后构建基于最小化调整成本的群决策算法，验证其收敛性，并将其应用于实例中。

1 基础理论

本章主要回顾一些基本概念，包括FJM、模糊判断矩阵的乘性一致性及其构造方法。

定义1[1]（FJM）假设X={x1,x2,…,xn}为一组待评价方案集合，N={1,2,…n}，则定义在方案集合X上的FJM 表示为P=(pij)n×n⊂X×X，其中元素满足pij∈[0,1]且pij+pji=1,pii=0.5,∀i,j∈N，这里的pij表示方案xi相对于xj的模糊偏好水平。

在FJMP=(pij)n×n中，元素pij=0.5 表示方案xi与xj优劣程度相当，元素pij ＞0.5 表示方案xi比xj优，并且pij越大，说明方案xi比xj越好。

定义2[16]（乘性一致性）若P=(pij)n×n是方案集X上的FJM，则其具有乘性一致性当且仅当：

2 基于最小化调整成本的群决策算法

本章首先引入衡量FJM 乘性一致性和FJM 之间共识水平的指数公式，包括一致性测度和共识性测度；然后设计了基于最小调整成本的共识调整反馈机制，以获得最优调整参数，使得所有不一致的决策者（decision maker，DM）满足最低调整成本的一致性阈值。该反馈机制包括识别机制和推荐机制。最后选择出最佳方案，并证明群体共识调整算法的收敛性。

2.1 一致性测度和共识性测度

显然，上述三个层面的一致性测度的取值范围均在[0，1]内，并且一致性测度值越大，说明该层面的一致性水平越高。

同样的，上述三个层面的共识性测度的取值范围也都在[0，1]内，并且共识性测度越大，说明该层面的共识水平越高。

注释1 虽然本文的一致性测度和共识性测度具有相似的构造结构，但是其含义不同。定义3在三个层面引入的一致性测度主要用于衡量单个FJM在偏好值、方案以及矩阵三个层面与其对应的完全乘性一致FJM 的距离，进而衡量单个专家提供的FJM 内部的一致性水平；定义4在三个层面引入的共识性测度主要用于衡量单个决策者提供的FJM在偏好值、方案以及矩阵三个层面与专家群体的综合FJM的距离，进而衡量该专家提供的FJM与外部专家群体之间的共识性水平。

2.2 基于最小调整成本的共识调整反馈机制

本节提出基于最小调整成本的共识调整反馈机制，使得所有不一致的DMs满足最低调整成本的一致性阈值。该反馈机制包括识别机制和定向推荐机制。

2.2.1 非一致专家的识别机制

识别机制旨在找出一致性或共识性水平低于给定阈值的DMs 及其需要调整的偏好。根据2.1 节中引入的一致性和共识性测度，给出如下定义来同时衡量DM的一致性和共识性水平。

定义5 DMs 在三个层面（即偏好值、方案和FJM）的一致性-共识性测度分别定义如下：

其中，参数α∈[0,1]表示一致性和共识性间的折衷系数。

一致性-共识性测度主要用于决定何时应用推荐机制，并用于构建最小调整共识模型，进而运用最优化模型获得最佳调整参数。因此，本文设计如下的非一致专家的识别机制，其主要包括三个步骤：

步骤1 在FJM层面确定一致性-共识性测度低于预先给定阈值γ的DM：

MLT={l|CCMl ＜γ}

步骤2 针对MLT中的DM，在方案层面确定一致性-共识性测度低于预先给定阈值γ的方案：

步骤3 找出满足步骤2 中条件的备选方案需要调整的偏好值，即在偏好值层面确定一致性-共识性测度低于预先给定阈值γ的偏好值：

2.2.2 定向推荐机制

在群共识调整的反馈过程中，由于最小成本的调整建议能够使得专家的初始偏好尽可能地保留，因此不一致的DMs愿意接受基于最优参数的调整建议。

假设决策者el提供的FJMPl=(plij)n×n的共识水平没有达到预先给定的阈值要求，那么可以依据综合FJMPC对Pl进行调整得到新的FJM如下：

其中，参数λl∈[0,1]表示el对综合偏好的接受系数。

特别地，当λl=0 表示el完全保留自己的初始偏好值，当λl=1 表示el完全接受群体偏好值观并做出最大妥协。因此，λl越大表示调整成本越高。

2.3 基于最小调整成本模型的最优调整参数确定方法

大多数的现有研究成果，一方面通常假设调整参数λl的值是预先给定的或固定的，却很少从优化的角度考虑；另一方面假设了所有需要调整的DMs具有相同的调整参数。然而，每个DM的共识水平及其与群体意见的偏差是不同的，因而每个非一致DM的调整参数应该不同。因此，需要将不同的调整参数分配给不同的非一致DMs。

因此，构建如下最小调整成本模型：

定理2 模型（13）等价于如下线性最优化模型（14）。

证明（1）根据FJM 中关于对角线对称元素具有的性质，易知将模型（14）中目标函数于模型（13）中目标函数等价。

因此有：

综上，定理2结论成立。

由于模型（14）是一个线性规划模型，因为目标函数和约束条件都是有界线性函数。根据线性规划理论，如果可行区域非空，则最优化模型（14）具有最优解，因此有如下结论：

定理3 如果最优化模型（14）存在可行解，则必然存在最优解。

注释2 参数α∈[0,1]表示一致性和共识性的折衷系数，这也能用于侧面反映专家在决策过程中的决策偏好。通过定义5可知，α越小，则一致性-共识性测度中的一致性测度比重增加，说明此时决策过程中的专家更加关注于单个FJM内部的一致性水平；α越大，则一致性-共识性测度中的共识性测度比重增加，说明此时决策过程中的专家更加关注于单个FJM与群体决策者之间的共识性水平。特别地，当折衷系数α=0 时，此时的最优化模型（13）就转化为如下的一致性调整成本最小化模型（16）：

为了保证最优化模型（14）存在可行解，需要设定合适的共识阈值γ。接下来，通过定理4可以确定决策者预先设定的共识阈值γ的上界γ*。

定理4 最优化模型（14）中共识阈值γ的上界能够通过如下最优化模型确定：

通过定理2 和定理4，可以使得预先设定的共识阈值γ不高于阈值上界γ*，从而确保最优化模型（14）存在最优解，于是能够计算出最小共识调整成本。

2.4 基于群体共识调整的群决策算法

算法1

第二阶段 根据2.1 节中的定义3 和定义4，分别计算出在FJM、方案、偏好值三个层面的一致性测度和共识性测度，然后运用2.2.1 小节的非一致专家的识别机制在三个层面来筛选出需要调整的偏好值。

第三阶段 运用定理4 确定共识阈值的上界γ*，并且使得预先设定的共识阈值γ≤γ*。

第四阶段 运用最优化模型（14）得到需要调整的DM 的调整参数λl，并依据2.2.2 小节中的定向推荐机制对Pl进行调整更新，逐步提升一致性-共识性水平。

3 案例分析

近年来，随着大数据、云计算等高新技术的发展和运用，基于深度学习的各种推荐系统产品逐渐发展并被应用于各个领域，并为处理复杂的大规模群决策问题提供了可行之路。随着新冠肺炎后疫情时代的持续发展和智能手机能设备的广泛普及，近两年在线上进行网购的人群规模迅速增加，这不仅给网上购物平台带来了机遇，也使购物平台面临着巨大的挑战[18]。某大型购物平台为了提升平台购物的客户体验和销售业绩，准备对购物平台原有推荐系统进行升级。该购物平台技术部门通过前期的调研和比较，在市场中筛选出四套备选的深度学习推荐系统{x1,x2,x3,x4}。为了优选出一套最佳的深度学习推荐系统对原有的购物平台推荐系统进行升级改造，该购物平台决策部们聘请深度学习和推荐系统领域的3 个专家{e1,e2,e3}对上面四套深度学习推荐系统进行评估和优选，从而提供了下面的3 个FJMPl=(plij)4×4(l=1,2,3)，专家的非负权重向量为W=(0.35,0.40,0.25)T。折衷系数α=0.6。

接下来，将运用基于群体共识调整的群决策算法（算法1）来优选最佳的深度学习推荐系统。

第二阶段 根据2.1 节中的定义3 和定义4，分别计算出三个专家在FJM层面的一致性测度和共识性测度，具体结果如下：

第三阶段 运用定理4计算得到该群决策问题群共识阈值的上界γ*=0.865 4。因此，本文假设预先设定的共识阈值γ=0.8 ≤γ*。

第四阶段 运用最优化模型（14）得到需要调整的三个专家的调整参数分别为：

λ1=0.296 7,λ2=0.194 5,λ3=0.438 6

并依据2.2.2 小节中的定向推荐机制对Pl进行调整更新，得到新的三个FJM如下：

于是调整后三个专家在FJM 层面的一致性测度和共识性测度，具体结果如下：

因此四套深度学习推荐系统的优劣顺序为x4≻x2≻x3≻x1，建议该网络购物平台选购深度学习推荐系统进行升级。

为了说明本文提出模型的共识调整效率，接下来将运用Zhang 等[19]提出的方法处理上述问题。Zhang 等[19]提出了五个标准，主要可分为两类：共识迭代次数和共识调整成本，但是其中的共识调整模型在执行过程中设定不同决策者的综合偏好接受系数λ相同，并且是随机选择[11-15]。为比较本文方法和文献[19]中的决策模型，下面设置决策者的综合偏好接受系数λ在区间[0，1]中每隔步长0.1取一次，并计算不同λ对应的共识调整次数、实现共识的调整成本以及在FJM层面的最低一致性-共识性水平，结果如表1所示。

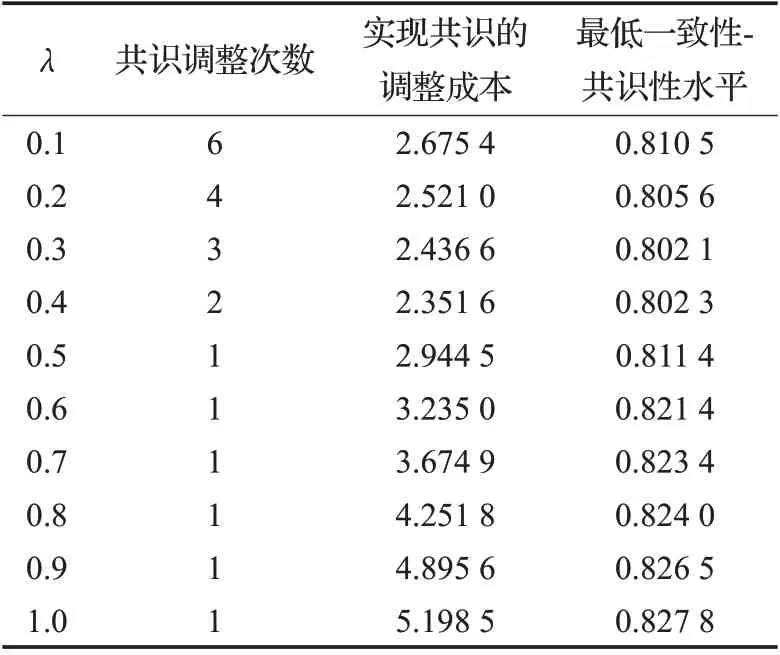
表1 文献[19]中运用不同λ 的共识调整结果Table 1 Consensus adjustment results using λ in [19]

从表1 可以看出，运用Zhang 等[19]中的共识调整模型处理上述问题，无论决策者的综合偏好接受系数λ取何值，在共识调整次数、实现共识的调整成本以及在FJM层面的最低一致性-共识性水平三个方面均没有本文基于群体共识调整的群决策算法得效果好。具体的，运用Zhang等[19]中的模型运用不同λ对应的共识调整次数均大于或等于本文决策模型的迭代次数1，运用不同λ实现共识所花费的调整成本均高于本文决策模型实现共识的调整总成本TCmin=2.198，运用不同λ实现共识之后在FJM 层面的最低一致性-共识性水平均高于0.8，而本文决策模型调整后的最低一致性-共识性水平刚好达到0.8。因此，通过本文群决策模型获得的群体共识恰好满足共识阈值条件，从而避免了对决策者意见的不必要调整和成本的浪费，这主要是因为本文群决策模型的调整参数针对不同的DMs 进行个性化设置，并通过求解优化模型进行选择，而现有文献则统一设置为所有DMs 的相同常数。综上，从成本和效率的角度来看，本文建立的基于群体共识调整的群决策算法在一定程度上优于现有的任意设置调整参数的共识调整方法。

4 结束语

本文主要在模糊信息环境下建立了基于群体共识调整的群决策算法，该算法首先针对所有非一致的DM都通过一致性和一致性度量的组合来识别；然后设计了基于最小调整成本的共识调整反馈机制，以获得最优调整参数，使得所有不一致的决策者DM满足最低调整成本的一致性阈值；最后建立基于群体共识调整的群决策算法，并验证算法的收敛性。深度学习推荐系统最佳方案的选择实例验证了本文群决策模型的优良特性。

本文建立的群决策模型虽然能够有效处理共识调整过程中的调整成本最小化问题，但是没有考虑大规模群体环境下的群体决策问题以及该环境下的专家权重如何计算。因此，在今后的研究中，将进一步探究大规模群体环境下基于最小化调整成本的群共识模型，分析大规模决策者的个性化最优调整参数，并挖掘基于统计推断的大规模群体专家权重计算模型，从而进一步提升群决策方法的可靠性。