大风区高速铁路接触网定位装置劣化规律研究
吴亚飞
(中铁第一勘察设计院集团有限公司,西安 710043)
引言
接触网定位装置连接接触网线索和腕臂,是高速铁路弓网系统的关键装备之一,其安全性、稳定性及抗疲劳性时刻受大风、异物等外部环境的影响[1-2]。在大风区挡风墙地段,大风经过后在挡风墙后部形成涡流区,会引起接触网线索剧烈振动,导致定位器摆动,长期以往会造成定位磨损,一旦脱落打弓,将会造成弓网设备损坏,严重时引起弓网事故[3-5]。为提高定位装置的结构可靠性,有必要研究大风条件下接触网定位装置劣化规律。
国内诸多专家学者对其开展了研究,常占宁、邓波等[6-7]分析了强风对接触网定位装置可能造成的影响,并从风偏设计、风速设计、装备选型优化等角度对接触网防风提出一些建议;田志军[8]较早对铁路沿线如高架桥、高路堤、风口及挡风墙等复杂环境下,特别是风口的高路堤区段引起风速增强及风向上吹角增加,对风区定位器抬升量给出了量化参考指标;曹树森、王迎波[9-10]采用有限元分析方法,以锚段关节为建模对象进行大风条件下动力稳定性分析,提出了适当减小接触线截面积及增加接触线、承力索初始张力等提升接触网防风性能的措施,为大风区接触网零部件选型提供指导依据;王玉环[11]针对我国大风区段强风对接触网支持装置的受力影响,提出一种新型防风腕臂结构,并通过有限元分析验证了其结构的合理性;谭德强[12]针对定位器与定位底座进行磨损性能分析,结果表明定位器与定位支座发生滑动状态下的相对运动时磨损量显著增加,并于定位器受力成正比;张若刚[13]提出定位器受正反两方向风的作用下会发生摆动,且受力较小时摆动频率加大,磨损加剧,同时提出调整参数及结构等措施,但并未深入研究风对定位装置的作用机理及劣化规律。综上可知,目前针对大风区高速铁路接触网定位装置劣化规律的相关研究较少,对接触网零部件仿真分析仍不够深入。
为辨析接触网定位装置力学性能劣化规律,需确定大风条件对接触网定位装置的影响程度,建立风区风场[14-15]、受电弓与含定位装置的接触网仿真模型,获取定位装置的时变载荷和时变位移,研究定位装置时变载荷与自身结构强度的力学性能关系。
1 大风条件下接触网定位装置仿真模型建立
根据表1新疆某高铁接触网设计参数,建立两个锚段接触网仿真模型,如图1所示。
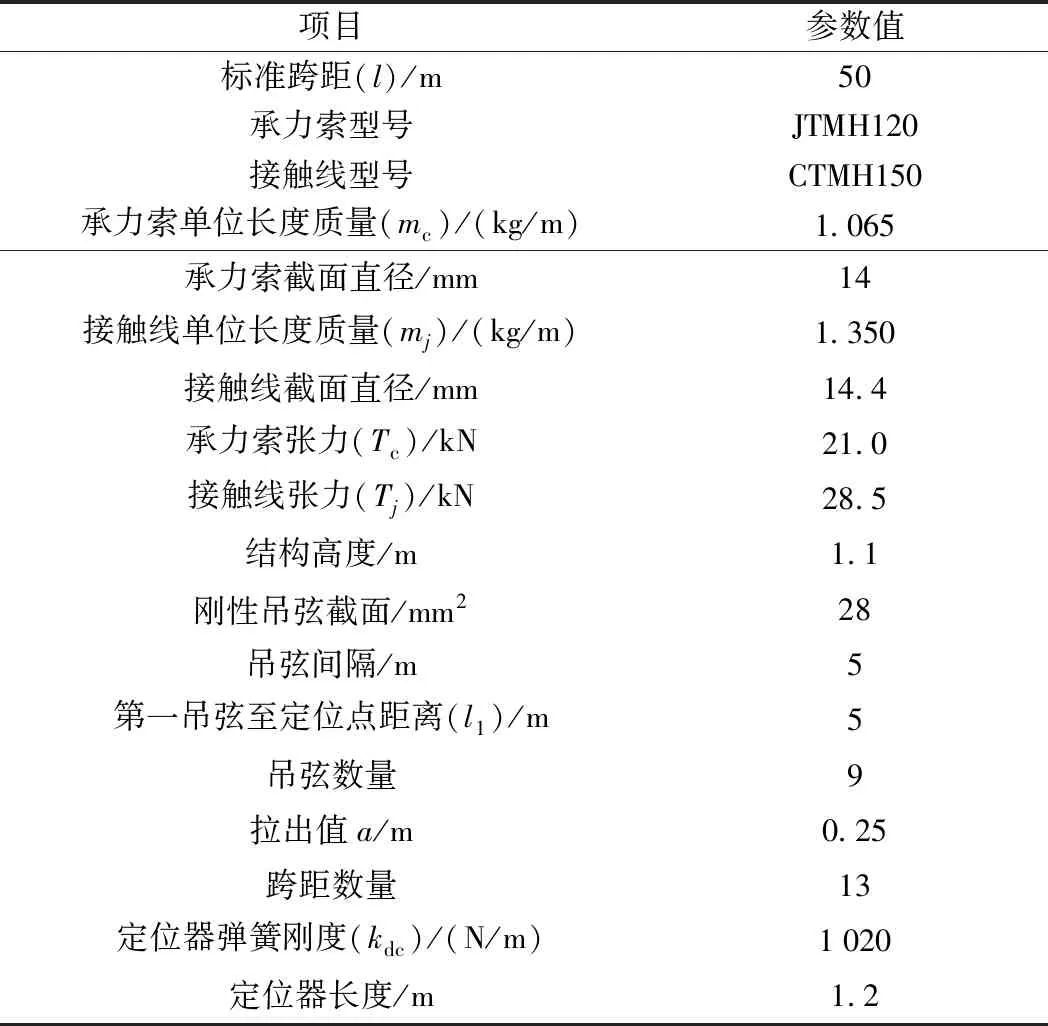
表1 新疆某高铁接触网设计参数

图1 新疆某高铁接触网仿真模型
脉动风速需利用结构建筑风载荷计算中常用的Davenport顺向谱和Panofsky竖向谱构造[16]。Davenport顺向谱模拟出水平脉动风速,风向为接触网模型的正z轴方向。Panofsky竖向谱模拟出垂向脉动风速,风向为接触网模型的正y轴方向。
根据多点相关风速谐波叠加模拟方法[17],利用MATALB软件编写生成接触网不同空间点的模拟风速[18]。按25 m取一个模拟风速特征点,风速特征点布置在跨中和腕臂支撑点,特征点的风载荷沿跨中和腕臂支撑点向两边12.5 m范围内均匀施加。
考虑新疆某高铁的地貌属于B类地区,地面粗糙度系数取0.16,接触线和承力索处风速按高度修正,地面阻力系数取0.002 16,假设时间步长为0.1 s,模拟时程总长为100 s,计算得到不同平均风速的50个特征点随机脉动风速时程(为区分平均风速,本文脉动风速包含平均风速),其中,特征点1的水平和垂向脉动风速曲线如图2所示。

图2 风速特征点1的脉动风速时程
图3为特征点1模拟脉动风速的自功率理论目标谱与模拟谱[19],两个谱特性非常接近,说明模拟的脉动风速精度较高。
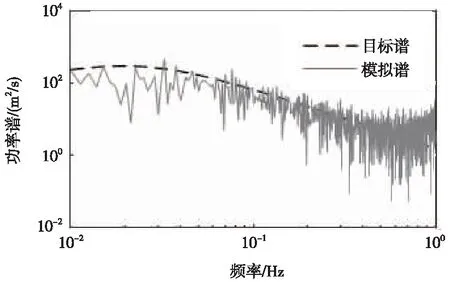
图3 风速特征点1的水平脉动风速功率谱
图4为特征点1和2、5、7、14、26、50水平脉动风速的互相关函数[20]。图中数字为归一化互相关函数的最大值,代表不同距离点的风速相关性强弱,数值越大,两特征点风速相关性越强。点1随线路中心方向距离的增加,依次与点2、5、7、14的相关系数逐步递减。点1与点26为同一线路中心位置,不同高度,体现出的风速相关系数最大为0.95,即同一断面上的风速变化不大。点1与点50间隔距离最远,其风速相关系数最小为0.16。不同特征点风速互相关函数的比较规律体现出多个风速随距离变化的相关性,说明模拟的脉动风速与实际风速规律相符。
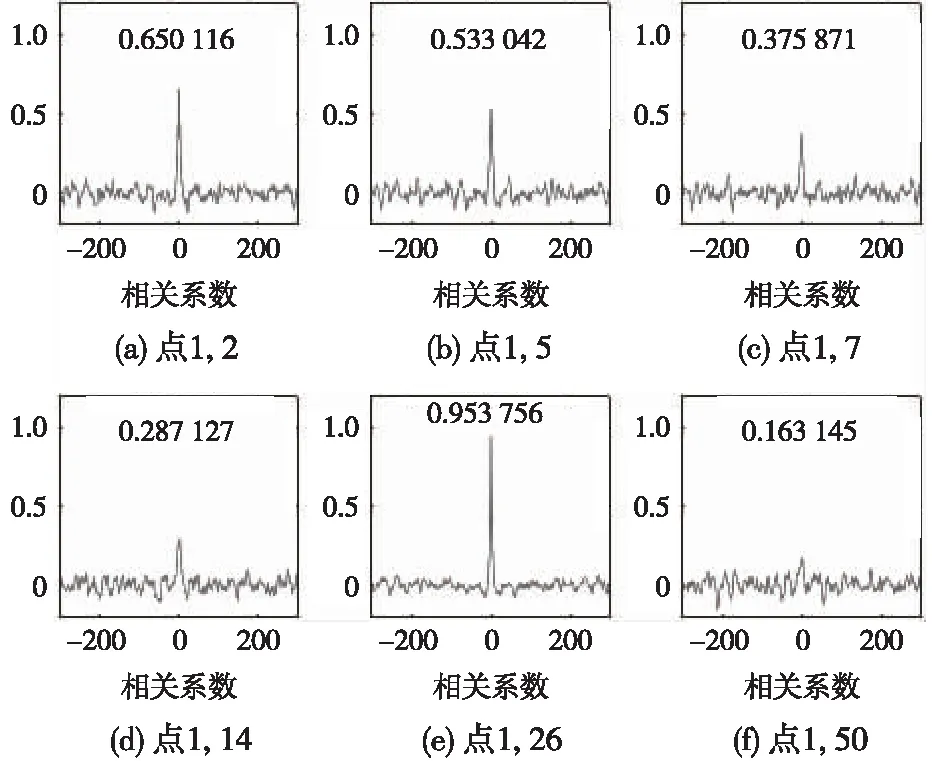
图4 不同接触网特征点水平脉动风速的互相关函数
统计风速谱生成的每个特征点脉动风速的瞬时最大值,为不失一般性,将各个瞬时最大值取算术平均,得到一定平均风速下的脉动瞬时最大风速,如表2所示,水平瞬时最大风速是平均风速的1.4倍左右,而垂直瞬时最大风速的变化较小。
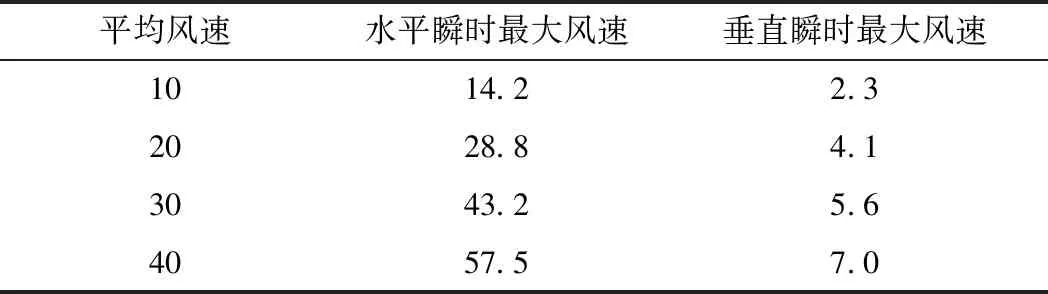
表2 不同平均风速下脉动瞬时最大风速比较 m/s
按接触网单位风载荷计算方法[21],得到承力索与接触线的单位长度风载荷,再根据线索有限单元长度,折算到接触网线索的每个单元节点。将脉动风施加到新疆某高铁接触网仿真模型上,如图5所示。
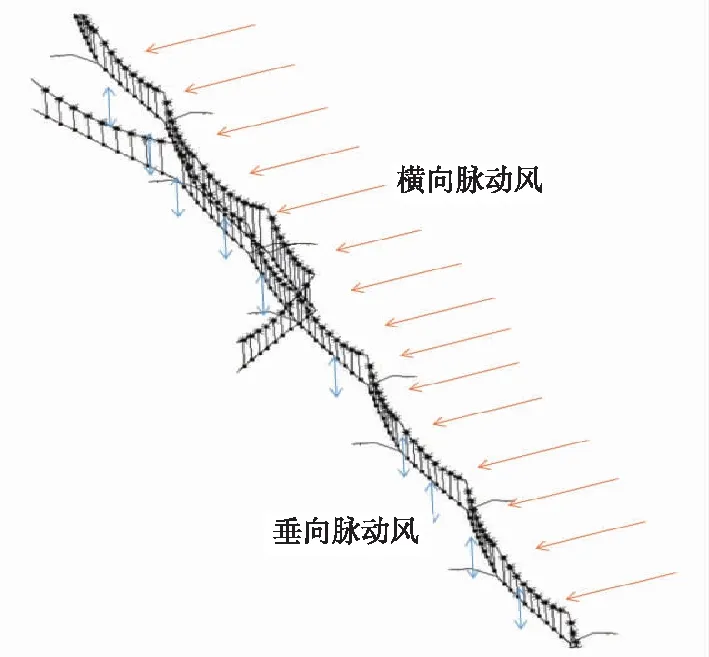
图5 接触网模型中的脉动风向
2 大风条件下接触网定位装置劣化规律研究
2.1 接触网分析区段选取
大风和受电弓作用于接触网上,引起锚段中不同部位的零部件位移和受力不同[22-23],为不失一般性,对比两个锚段的锚段中部四跨非绝缘关节,跨距编号从小到大(1~8)排序与受电弓运行方向一致,如图6所示。

图6 接触网仿真模型分析区段
为便于分析,将接触网仿真模型中的定位装置分析位置标识在图7上(跨距编号不变)。红色为第1锚段,蓝色为第2锚段,均为7个定位,横风自上往下吹。

图7 接触网定位装置分析位置
2.2 恒定风速下定位器劣化规律分析
分析30 m/s平均风速的脉动风作用下不同定位点的振动规律。绘制1~4号定位点二维位移的散点密度图,如图8所示。
1号、3号定位点位于沿x轴正向的第1个、第3个定位器,靠近风源侧,定位点垂向位移范围为-0.017~0.020 m,且平均位移大于0;反之,远离风源侧2号、4号定位点垂向位移范围为0.01~-0.03 m,且平均位移小于0;横向摆动范围2~4 mm。远离风源侧的定位点受到的“之”字力较小,受电弓作用下该类定位点的抬升量较大[24];且脉动风引起的摆动幅度比靠近风源侧大,故远离风源侧定位器根部的磨损量相对较大。
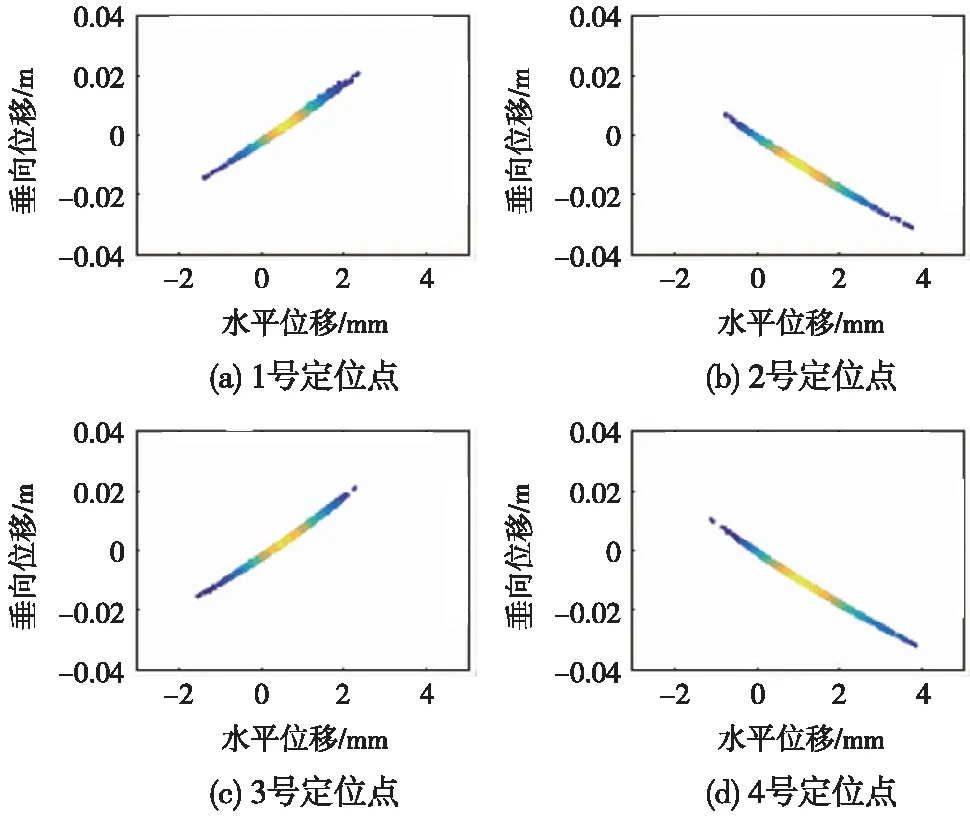
图8 相邻定位点位移散点密度图
将1号、2号定位点垂向位移进行高阶中值滤波处理,得到每时间段的平均值连续曲线,如图9所示。远离风源和靠近风源的两类定位点垂向位移随时间有周期性地靠近和远离运动,轨迹基本对称,抬升最大幅值基本接近,约为7 mm,说明脉动风作用下远离风源和靠近风源的两类定位点垂向位移的运动方向相反。

图9 中值滤波后的定位点垂向位移曲线
2.3 不同风速条件下定位器劣化规律分析
绘制不同风速下接触网定位点抬升和定位支座受力变化曲线,如图10~图13所示。通过对比可以看出,相同风速下,靠近风源侧的定位点最大抬升和定位支座反力相对远离风源侧较大;风速越大,靠近风源侧的定位点最大抬升和定位支座反力越大,且增加速度相对远离风源侧较快。
通过对比发现,定位点最大抬升为108 mm,定位支座反力为1 870 N,均出现在靠近风源侧,分别见图12、图13。可以得出,靠近风源侧的定位器与定位支座的磨损行程和摩擦力较大。轴销摩擦副的磨损行程和摩擦力是影响摩擦副磨损量的关键因素[25],因此,靠近风源侧的定位装置出现磨损失效的风险较其他定位点高,其磨损寿命相对较低。
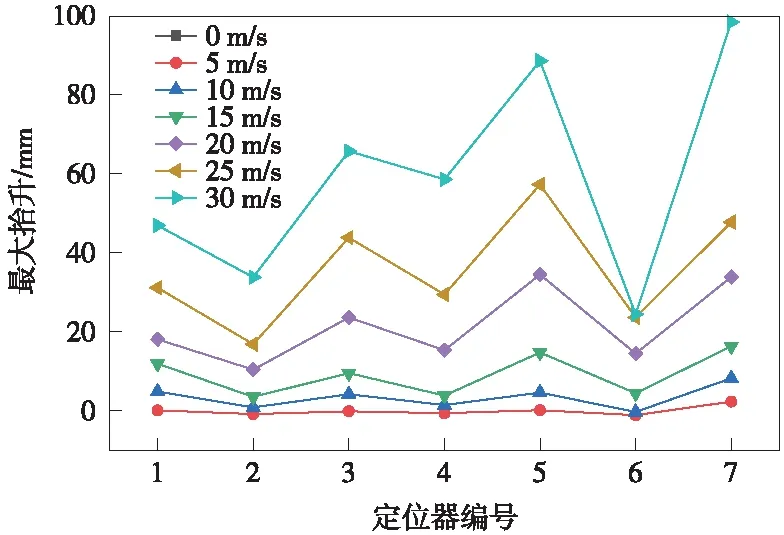
图10 第1锚段定位点最大抬升变化曲线(大风作用下)
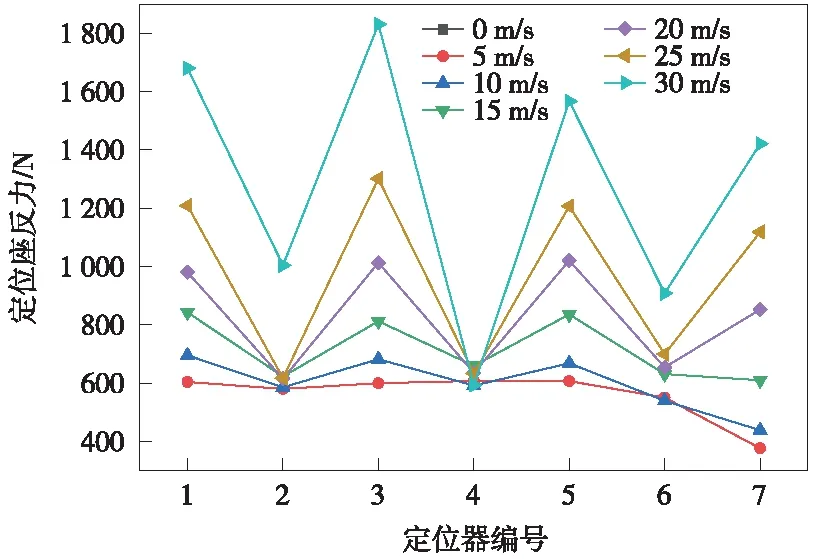
图11 第1锚段定位支座反力变化曲线(大风作用下)
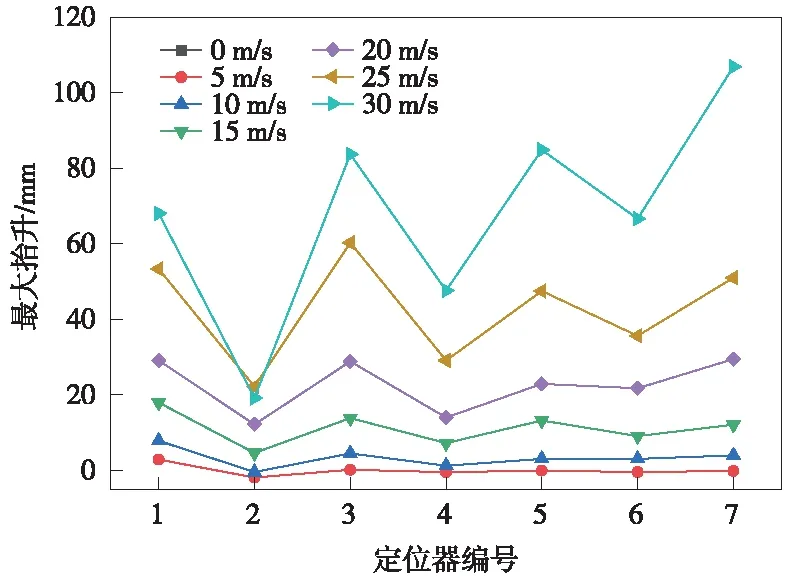
图12 第2锚段定位点最大抬升变化曲线(大风作用下)
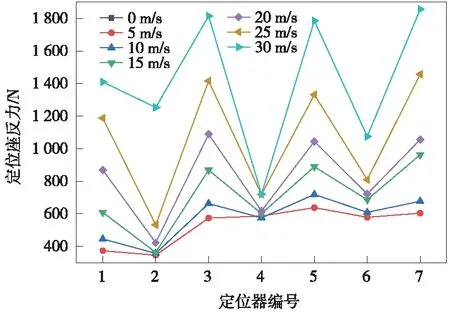
图13 第2锚段定位支座反力变化曲线(大风作用下)
大风和受电弓作用下接触网定位点抬升和定位支座受力变化曲线,如图14~图17所示。
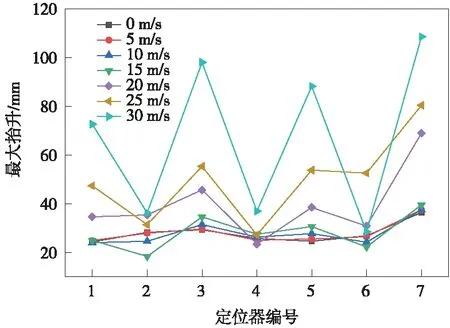
图14 第1锚段定位点最大抬升变化曲线(大风和受电弓作用下)

图15 第1锚段定位支座反力变化曲线(大风和受电弓作用下)
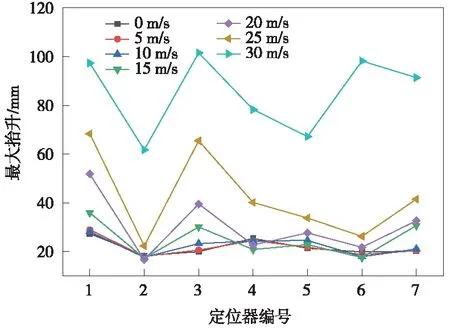
图16 第2锚段定位点最大抬升变化曲线(大风和受电弓作用下)
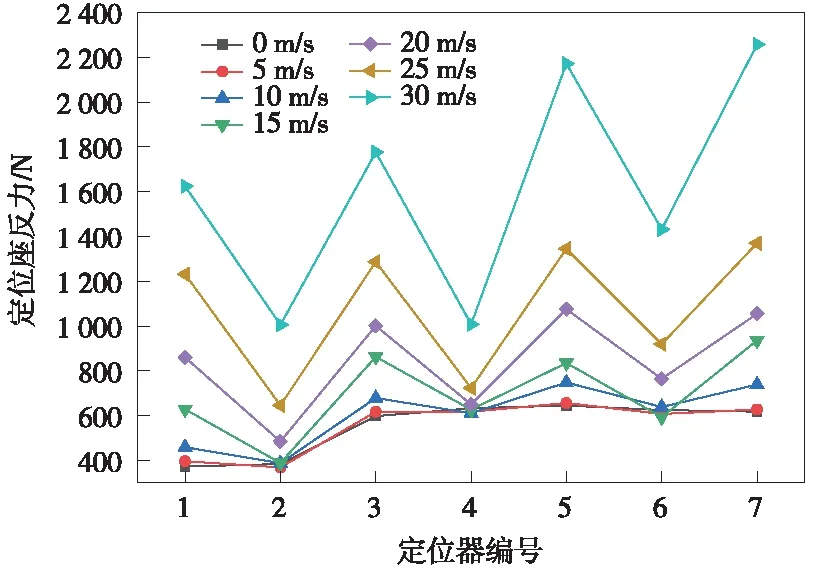
图17 第2锚段定位支座反力变化曲线(大风和受电弓作用下)
经对比,当受电弓通过大风作用下接触网,风速为30 m/s时,定位点最大抬升110 mm,定位支座最大反力为2 280 N,分别见图16、图17。对比同一锚段受电弓作用前后,定位点最大抬升和定位支座反力较仅有大风作用时均有所增加,且定位支座增幅达22%。
3 结语
通过有限元分析方法,建立了含定位装置的弓网动态仿真模型,模拟脉动风并利用互相关函数验证了模拟风载荷的有效性,最终折算成垂向和横向脉动风荷载施加到弓网动态模型。应用弓网动态仿真模型,在恒定风速和不同风速两种条件下进行了定位装置的劣化规律研究,得出主要结论如下。
(1)恒定风作用下,靠近风源侧定位点垂向平均位移大于0,而远离风源侧小于0,且摆动幅度和磨损量相对大;二者垂向运动轨迹呈对称状态。
(2)相同风速下,靠近风源侧的定位点最大抬升和定位支座反力相对远离风源侧较大;风速为30 m/s时定位点最大抬升为108 mm,定位支座反力为1 870 N;靠近风源侧定位装置出现磨损失效的风险较其他定位点高,其磨损寿命相对较低;风速越大,靠近风源侧的增加速度相较远离风源侧更快。
(3)相较于仅有大风作用时,受电弓与大风共同作用下定位点最大抬升和定位支座反力均有所增加,且定位支座反力增幅达22%,说明受电弓对接触网作用的影响不容忽视。
(4)大风区高速铁路接触网定位装置在标准制定、产品设计及选型时,较常规区域应考虑脉动风横向和纵向的作用后对定位装置磨损、疲劳及受力性能等方面影响。

