微视频先导实现数学课堂的深度学习*
———“幂函数(第1课时)”的教学设计与思考
200040 上海市市西中学 张 娜
教育部基础课程教材发展中心推出的《深度学习:走向核心素养》一书对深度学习给出如下定义:“所谓深度学习,就是指在教师的引领下,学生围绕着具有挑战性的学习主题,全身心积极参与,体验成功,获得发展的有意义的学习过程.”图1呈现出深度学习的几项基本特征:联想与结构、活动与体验、本质与变式、迁移与应用、价值与评价.
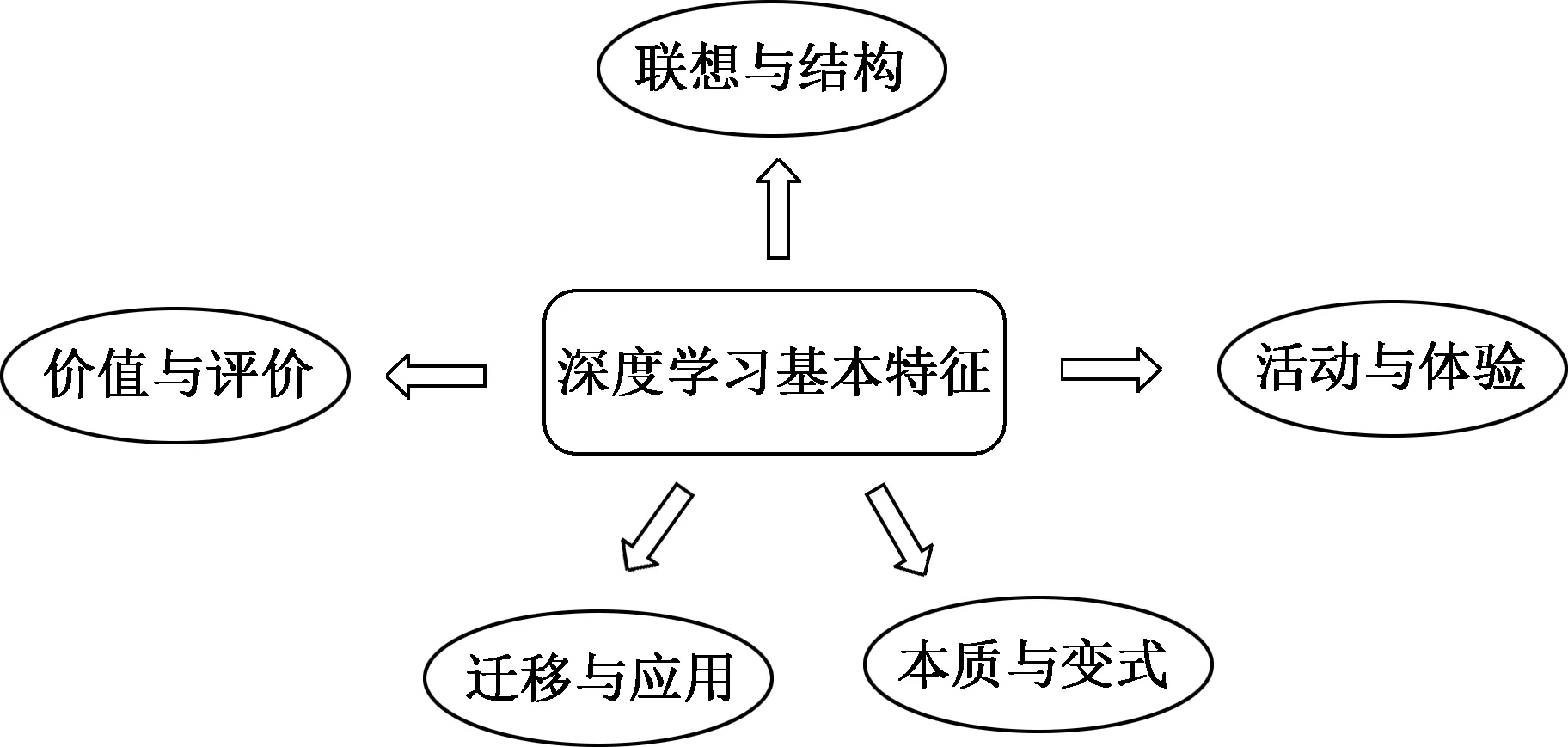
图1
那么,如何更好地让学生在课堂中完成深度思考,达成深度学习?笔者采取微视频先导下的课堂教学方式.在学生通过微视频预习达成统一的、更高的认知起点基础上,在课堂教学中完成对具有挑战性问题的探究.笔者以“幂函数(第1课时)”的教学设计为例,呈现如何在数学课堂中达成深度学习.
一、教学设计的理念与背景
2020年9月以来,上海市高中数学学科开始实行“新课标”“新教材”的“双新”课程,本次课程改革特别强化基于课标的教学,在教学设计的过程中强调目标导向,突出重点,突破难点,注重知识发生、发展的过程,将资源、评价、指导融入活动之中.
在上述教学设计理念的引领下,笔者采取微视频先导下的课堂教学方式.经过长期的课堂教学实践与探索,将微视频先导下的教学过程凝炼为五个环节,即“目标引领—自主预习—评价反馈—释疑深化—合作探究”.基于以上教学设计理念与背景,笔者展开如下教学设计.
二、教学目标
(1)理解幂函数的概念,经历通过列表、描点、连线的方法作出具体幂函数图像的过程,感受幂函数在第一象限的图像特征.
(2)用代数的方法研究幂函数y=xa(a>0)在区间(0,+∞)上为严格增函数的性质,体会逻辑推理的重要性.
(3)在幂函数图像与性质的探究过程中,体会从特殊到一般的研究方法,感悟数形结合的数学思想,学会用数学语言对严格增函数的性质进行严谨的逻辑表达.
三、教学重点、难点
教学重点:理解幂函数的概念,作出具体幂函数的图像,知道幂函数的性质.
教学难点:在研究幂函数图像与性质的过程中,经历从几何直观到代数说理的逻辑推理过程.
设计意图:在初中期间学生已经学习了一些基本的初等函数,如正比例函数、反比例函数、一次函数、二次函数等.在此基础上,幂函数的学习是进一步研究在等式ab=c中,字母b的取值固定时,另两个量的相互关系和变化规律,同时学会用幂函数图像与代数推理的方法研究幂函数的性质,也为下一章“函数的概念、性质及其应用”的学习奠定基础.基于幂函数这一节内容的重要作用,笔者从学生的视角出发,制定以上教学目标并设定教学重点、难点.
四、自主预习
在课前,学生通过观看微视频进行自主预习并完成配套基础题.
微视频主要包含以下几个方面的内容.
(1)幂函数的概念.
(3)根据给定幂函数的图像判断幂指数的大小关系.
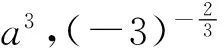
微视频的配套基础题如下.
题1在同一直角坐标系中作出y=x,y=x2,y=x-1,y=x0的图像.
题2填写表1.
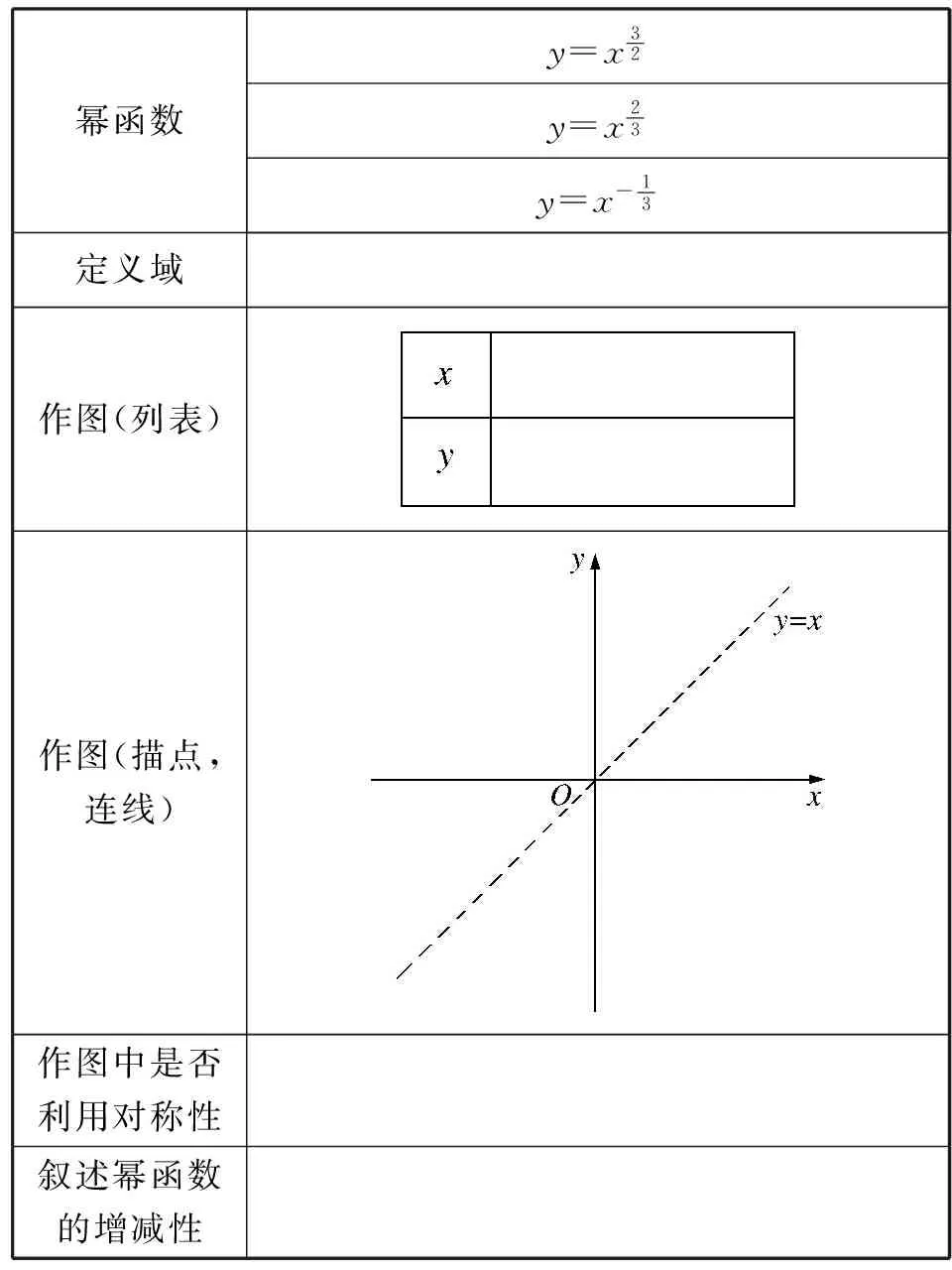
表1
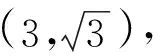
(2)幂函数y=x-m2+2m+3(m∈Z)的定义域为R,求字母m的值.
(3)比较2.5-3与3.1-3的大小,并说理.
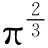
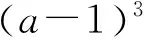
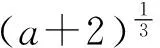
设计意图:在课前,学生通过观看微视频知道了幂函数的概念,能够求具体幂函数的定义域,通过列表、描点、连线并结合图像的对称性作出具体幂函数的大致图像,并能够通过观察幂函数的图像叙述其所具备的一些性质,在此基础上进入课堂教学.
五、课堂教学过程
(一)评价反馈
1.评价
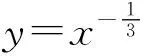
教师活动在学生提交的基础题答案中分别选取不规范表达与正确表达进行投影比对,让学生结合函数单调性的定义进行自主评价,从而完成对不规范表达的订正.
学生活动对教师呈现的不同答案进行对比思考,结合单调性定义纠正可能存在的不规范表达,对指数为负数时幂函数的增减性有更准确的把握.
2.反馈
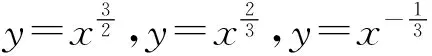
问题1这几个幂函数的图像是否恒过定点?
预设回答:恒过定点(1,1).
问题2对于一般的幂函数y=xa(a∈R)是否也过此定点,为什么?
预设回答:是的,因为1的任何次幂都等于1.
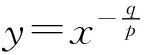
预设回答:具备,关于原点对称.
问题4这类幂函数图像是否经过定点(1,1),除了(1,1)之外是否还有其他定点?
预设回答:是的,还有定点(-1,-1).
问题5请描述这一类幂函数的单调性.
预设回答:在(-∞,0)和(0,+∞)上分别为严格减函数.
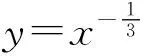
(二)释疑深化

预设回答:因为幂指数是无理数,故无法通过不等式的基本性质或作差的方法进行证明,只能选用幂的基本不等式.

设计意图:释疑深化环节是本节课中的难点突破,在沪教版新教材中,幂指数从老教材中规定的有理数扩大到实数范围,并要求学生通过幂的基本不等式完成对幂函数的增减性的说理,这对学生提出了很高的要求.因此,笔者在课前预习时就对此难点的突破进行了铺垫,在预习基础题中让学生先从几何的直观感悟出发,再到课堂中通过教师的引导经历从几何直观到代数说理的逻辑过程,在证明的过程中笔者也将学生的关注点聚焦在相对简单的第一象限,也就是让学生探索当x∈(0,+∞)时幂函数增减性的说理,这也从一定程度上降低了说理的难度.
(三)合作探究
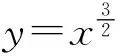
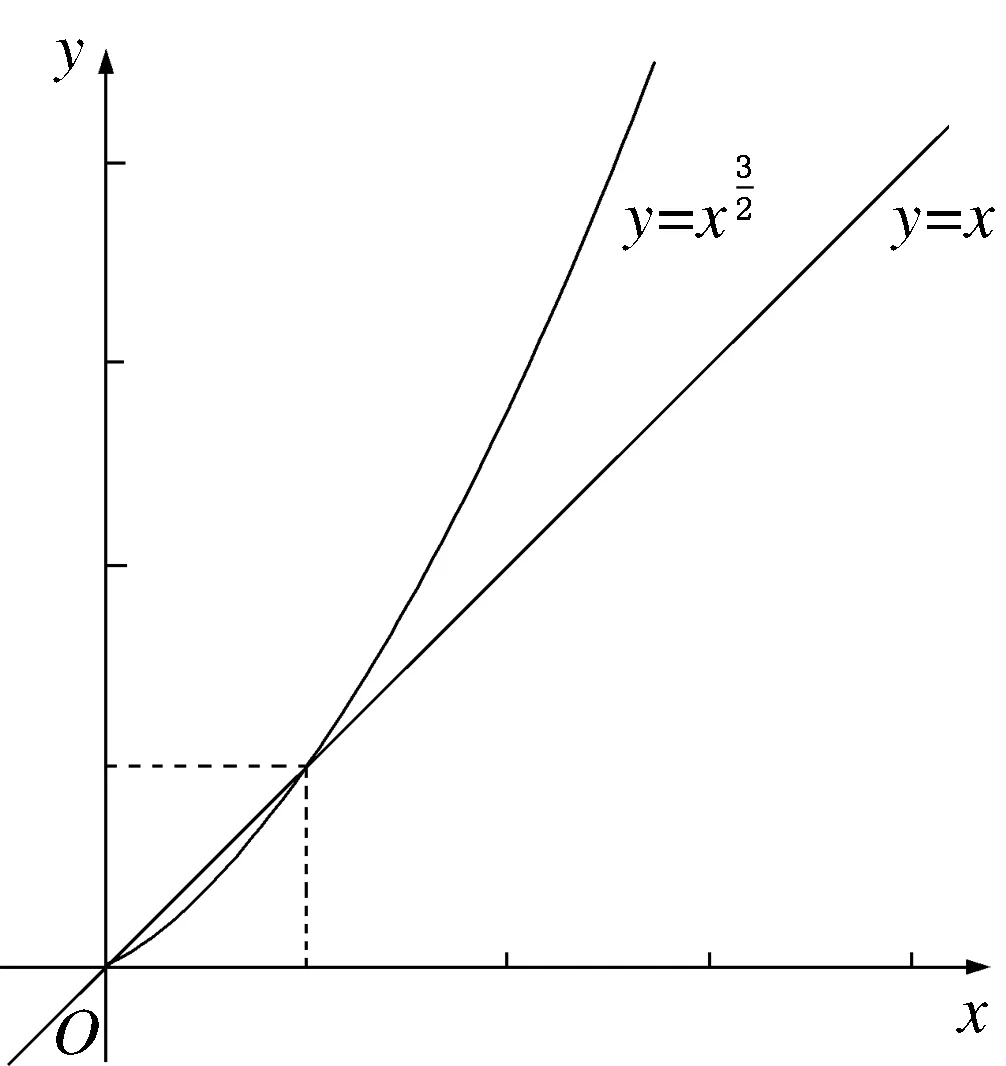
图2
问题1将此函数图像的特征转化为代数表达并进行严格说理.
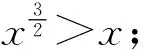
问题2请通过小组合作探究的方式思考对于一般的幂函数y=xa(a≠1),当字母的取值范围为多少时符合上述函数图像特征,并进行严格说理.
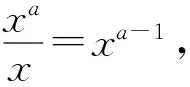
学生活动仔细观察教师提供的两个特殊幂函数的图像特征并将其转化为代数表达,借助不等式的基本性质进行严格说理.通过小组合作探究的形式完成对一般幂函数y=xa(a>1)图像特征代数表达的深度思考,并通过幂的基本不等式完成严格说理.
设计意图:本环节通过合作探究的方式旨在落实沪教版新教材中通过幂的基本不等式进行幂函数性质说理的要求,这对学生来说是有挑战性的问题.本环节从幂函数图像的特征出发逐步转化为代数说理,其中特别需要关注的是指数a是在实数范围内,这也是沪教版新教材与老教材的关键区别所在.在老教材中,指数a限定在有理数的范围内,函数单调性与图像特征的说理都可以通过不等式的基本性质完成,而新教材将指数a扩大到了实数的范围内,那么函数单调性与图像特征的说理都只能通过幂的基本不等式完成.在释疑深化环节中完成对具体幂函数单调性证明之后,通过合作探究的形式进一步探索一般幂函数图像特征,并借助幂的基本不等式进行严格说理,关注和提升学生逻辑推理的数学核心素养.
(四)课堂小结
1.总结幂函数在第一象限中的图像特征.
2.通过幂的基本不等式证明当x∈(0,+∞)时,幂函数y=xa(a>0)是严格增函数的性质.
3.通过小组合作的方式,依据幂的基本不等式对幂函数的图像特征进行代数说理.
六、课后总结与反思
(一)微视频先导下,课堂教学容量更大,学生的课堂参与性更高
从本节课的整体教学设计可以看出,虽然是幂函数的第1课时,但是幂函数图像与性质的重点内容都在课堂教学中得以体现,课堂容量大、学生参与度高,这些都得益于学生在课前通过观看微视频进行自主预习.在课前,学生已经对幂函数的概念以及通过列表、描点、连线作出幂函数的图像进行了充分的准备与熟悉,形成了统一的、更高的认知起点.微视频特别为一些新知接受能力较弱的学生提供了充足的缓冲、消化时间,为课堂教学的高效、顺利展开做足了铺垫.
(二)课堂聚焦学生深度学习,注重学生在自主思考与小组合作下逻辑推理核心素养的提升
在形成统一的、更高的认知起点之后,教师依据学生课前基础题的完成情况,在课堂教学中重点聚焦学生新知学习过程中所产生的误区与盲点进行重点突破.本节课的课前基础题反馈出学生对幂函数图像对称性与增减性的文字表达以及代数逻辑表达都存在较大问题.因此,在练习反馈环节教师重点对学生的薄弱环节进行点评、比较、讨论,纠正学生的表达问题以及理解误区,又在后续的释疑深化环节以及合作探究环节针对幂函数图像特征的代数说理进行集中突破,促成学生在自主思考与小组合作下逻辑推理核心素养的显著提升.
(三)为“挑战性”问题的深入思考预留足够空间,让课堂真正成为学生探究性学习的“学堂”,助推教学目标的达成,从根本上改善课堂教学环境
在微视频的先导下,课堂为具有挑战性问题的解决预留了足够的空间,如本教学设计中借助幂的基本不等式完成对幂函数图像特征代数说理的突破,同时也为深入的师生对话与生生对话提供了可能.这从根本上改善了传统课堂教学中(特别是在概念性教学中)教师知识传授为主的沉闷课堂环境,让学生真正成为课堂的主导者,让课堂真正成为学生进行探究性学习的“学堂”.

